地球表面两点间最短距离

知道两点经纬度求两点距离公式计算两点之间的距离是地理学中的一个基本问题。

在计算两点距离之前，我们首先需要明确计算距离的参考系。

通常情况下，我们使用经度（表示东西方的位置）和纬度（表示南北方的位置）来确定地球上的位置。

在计算两点之间的距离时，我们可以使用不同的方法。

其中，最常用的方法包括欧几里得距离、大圆距离和球面三角法。

1.欧几里得距离：欧几里得距离又称为直线距离，它是二维欧几里得空间中两点之间的直线上的距离。

对于平面上的两个点(x1,y1)和(x2,y2)，欧几里得距离公式如下：d=√((x2-x1)²+(y2-y1)²)然而，由于地球是一个球体而不是一个平面，欧几里得距离并不适用于计算地球上两点之间的距离。

2.大圆距离：大圆距离也称为球面距离，它是地球上两点之间沿着地球表面的最短距离。

大圆距离公式如下：d=R*θ其中，R是地球的半径（通常取平均半径6371公里），θ是两点之间的中心角。

计算大圆距离时，我们需要先将经纬度转换为弧度，然后使用球面三角法计算中心角。

3.球面三角法：余弦定理公式如下：cos(c) = cos(a) * cos(b) + sin(a) * sin(b) * cos(γ)其中，a和b是两个点分别与地球球心的连线与地球赤道的夹角，c 是两个点之间的中心角，γ是两个点之间的经度差。

为了计算中心角，我们需要首先将经纬度转换为弧度。

对于两个经纬度坐标点（φ1,λ1）和（φ2,λ2），其中φ表示纬度，λ表示经度，转换公式如下：φ = latitude * π / 180λ = longitude * π / 180然后，就可以使用余弦定理计算两点之间的距离了。

以上这些方法都可以计算两个经纬度坐标之间的球面距离。

对于一些较短距离的计算，例如在城市范围内，使用欧几里得距离可能是比较准确的。

对于大范围距离的计算，推荐使用球面三角法。

最后，还需要注意的是，上述公式都是基于地球模型的简化情况，实际地球的形状更接近于一个略扁的椭球体。

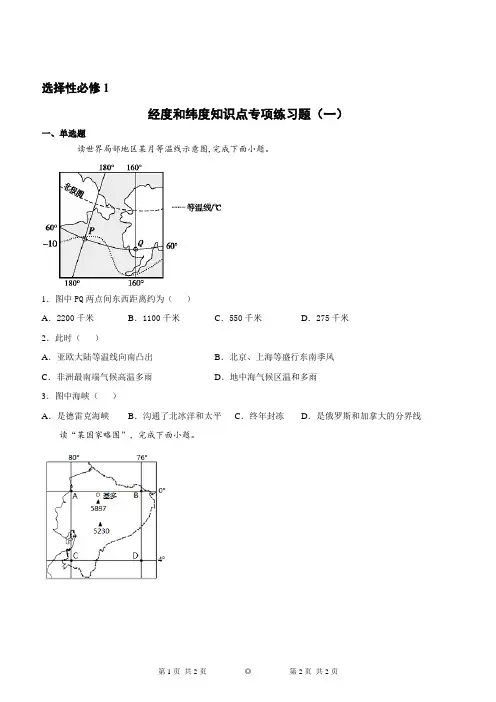
选择性必修1经度和纬度知识点专项练习题（一）一、单选题读世界局部地区某月等温线示意图,完成下面小题。

1．图中PQ两点间东西距离约为（）A．2200千米B．1100千米C．550千米D．275千米2．此时（）A．亚欧大陆等温线向南凸出B．北京、上海等盛行东南季风C．非洲最南端气候高温多雨D．地中海气候区温和多雨3．图中海峡（）A．是德雷克海峡B．沟通了北冰洋和太平C．终年封冻D．是俄罗斯和加拿大的分界线读“某国家略图”，完成下面小题。

4．图中国家所在的大洲是（）A．非洲B．大洋洲C．南美洲D．亚洲5．图中两座山位于（）A．北半球西半球B．北半球东半球C．南半球西半球D．南半球东半球6．图中城市基多位于北京的（）A．东南方B．东北方C．西南方D．西北方7．图中四段线段实际长度的比较，正确的是（）A．AB=AC=CD=BD B．AB=AC=BD>CD C．AC=BD>AB>CD D．AB>AC=BD>CD全球卫星导航系统（GNSS）技术可用于定位、导航。

若甲、乙两地的信号接收机显示的经纬度坐标为甲（80°25'01″N,77°06'58″E），乙（69°22'24″N,76°22'40″E）。

据此完成下列小题。

8．甲、乙两地的直线距离约为（）A．820千米B．1220千米C．1020千米D．1420千米9．甲地在乙地的（）A．西北方B．西南方C．东北方D．东南方10．晴朗的夜晚,同一时间两地观测到北极星的状况是（）A．两地都刚好露出地平线B．甲地看到的北极星仰角大于乙地C．甲地看到的北极星仰角小于乙地D．都看不到北极星北极航道是连接大西洋和太平洋的海上捷径。

随着全球气候变暖，北极冰区逐渐缩小，北极航道的商业价值越来越得到人们的关注。

自2013年“永盛”轮首航北极东北航道以来，中国货轮已经多次航行在这条航线上。

专题01 地球与地图考点帮你练一、选择题（2021·江苏高三零模）尼泊尔拥有多条著名徒步旅行线路，是世界徒步旅行胜地。

2019年10月，小明乘机抵达加德满都，然后乘汽车前往博克拉，开始沿图示线路顺时针徒步旅行。

下图示意旅行线路及行程安排。

据此完成下面小题。

1．若汽车时速为50千米，小明从加德满都前往博克拉大约需要（）A．2小时B．4小时C．6小时D．8小时2．北京时间12：00时，小明在徒步前行中发现太阳位于自己的右前方，此时小明最可能位于（）A．①处B．②处C．③处D．④处【答案】1．B2．B【分析】1．从图中可知，加德满都和博克拉经度相差大约2°，两地纬度都接近30°，可以计算出两地距离为111千米×2×cos 30°，加上公路线的弯曲估算大约为200千米，汽车时速为50 千米，故大约需要4小时。

故选B。

2．根据所学知识可以计算出，当北京时间12∶00时，当地地方时在10;00 之前，正处于上午，太阳位于东南方。

由图中可以看出，当小明在②处时正向东走，太阳在其右前方，B正确。

③④处向南走，太阳位于左侧，C、D错误。

①处向西北方向走，太阳位于后方，A错误。

故选B。

（2021·北京高三一模）中国南极考察主要有三条航线：a航线（弗里曼特尔港一中山站）、b航线（霍巴特港一中山站）、c航线（利特尔顿港－长城站）。

读图,完成下面小题。

3．我国选择a航线的次数最多，主要考虑的是（）A．航程最短B．沿途补给C．顺风顺水D．避开海雾4．c航线（）A．跨越了南温带与南寒带B．跨越了日界线C．考察船上国旗常飘向东北D．考察船向东航行【答案】3．A4．B【分析】3．由图可知，与其他航线比较，a航线（弗里曼特尔港一中山站）航程最短，A正确；由图文材料无法推测a航线是否有沿途补给，B错误；a航线需穿越西风带和西风漂流，C错误；海雾主要是在寒暖流交汇海区或寒流经过的温暖海区或暖流经过的纬度较高的海区，与其他航线比较，a航线海雾状况不好判断，无特殊之处，D错误。

球面距离的几种证明方法
球面距离是指在椭球面上，任意两点之间的最短路径，它是椭球面上任意两点的距离。

在地球表面的航行中，球面距离是最常见的几何距离，它以地球表面的维度和经度表示。

需要定义两点的维度经度，使用数学计算就能求出两点之间的球面距离，求出的球面距离与实际距离无论大小都有较大的差异，所以球面距离的应用非常广泛。

在此，本文将介绍几种球面距离的证明方法。

第一种证明方法：三角形证明法。

通过建立两点之间的三角形，定义出三条边长，利用三角形和地球球面之间的特殊关系，可以计算出三角形的面积，进而确定两点之间的球面距离。

第二种证明方法：空间分析法。

通过对两点之间连接的弧的长度和圆心角的空间分析，可以求出两点之间的球面距离。

第三种证明方法：旋转投影法。

这种证明方法基于地球球面的旋转特性，将空间点图投影到局部圆锥曲面上，求出局部圆锥曲面上的距离，最终得出两点之间的球面距离。

第四种证明方法：GPS定位法。

GPS定位法是利用GPS定位技术，根据卫星定位两点坐标，通过计算得出两点的经纬度和高度，最后求出两点之间的球面距离。

第五种证明方法：椭球体参数法。

地球表面最短距离的计算摘要：本论文探讨在仅知经纬度的情况下，地球表面最短距离计算的问题。

本文通过利用极点、已知地点的地理坐标构建球面三角形，引入球面三角形的第一五元素公式；用经纬度代换公式中的球心角的角度（弧度），成功的解决了利用经纬度计算地球表面任意两地间最短距离的问题。

导出了通过经纬度求两地最短距离的公式，并简化了特殊情况下的计算公式。

非常适合于地理学习、全球定位与导航等问题中的最短距离计算。

（球面距离）=2πR•arcos[sinW1sinW2+cosW1cosW2cos(J1-J2)]/3600关键词：经纬度，球面距离，球面三角形，第一五元素公式，反余弦在地理科学的学习与应用中，我们时常遇到求地球表面两地间最短距离的情况。

在条件特殊时：如两点都在赤道上、或在同一经线上时较容易。

但当两地不再同一经线或赤道上时我们就难以获得准确答案。

笔者经过长时间的思考学习，总结了球面上任意两点间距离的计算方法，效果不错。

现介绍如下，以供大家参考。

1.公式推导球面距离，就是球面上经过这两点的大圆的劣弧的长度。

而地球表球面上每个地点的位置是由经度、纬度来确定的，如果能利用经纬度来计算球面距离，我们就可以确定任意两地间的球面距离（不考虑地形影响，下同）。

如左图：设M （W1，J1）、L（W2，J2）为地球表面两点，N为极点，表示两点之间的最短距离（球面距离），、分别表示极点至M、L的经线长。

依球面三角形概念可知：N、M、L共三点构成了球面三角形NML的三个顶点，、、构成了球面三角形的三条边。

它们的夹角、弧度、弧长等可根据球面三角形的性质进行相关计算得出。

为方便计算，按经纬度划分原则，将东经记为正，西经记为负；北纬记为正，南纬记为负。

例；东经60度记作J= +600、西经60度记作J =-600、北纬60度记作W=+600、南纬60度记作W=-600；用a、b、c分别表示三条边、、所对应的球心角，W1 W2分别M、L纬度,J1J2分别表示M、L两地的经度，A表示两地所在经线的夹角且小于1800，R为地球半径。

地球表面最短距离的计算摘要：本论文探讨在仅知经纬度的情况下，地球表面最短距离计算的问题。

本文通过利用极点、已知地点的地理坐标构建球面三角形，引入球面三角形的第一五元素公式；用经纬度代换公式中的球心角的角度（弧度），成功的解决了利用经纬度计算地球表面任意两地间最短距离的问题。

导出了通过经纬度求两地最短距离的公式，并简化了特殊情况下的计算公式。

非常适合于地理学习、全球定位与导航等问题中的最短距离计算。

（球面距离）=2πrarcos[sinw1sinw2+cosw1cosw2cos(j1-j2)]/3600关键词：经纬度，球面距离，球面三角形，第一五元素公式，反余弦在地理科学的学习与应用中，我们时常遇到求地球表面两地间最短距离的情况。

在条件特殊时：如两点都在赤道上、或在同一经线上时较容易。

但当两地不再同一经线或赤道上时我们就难以获得准确答案。

笔者经过长时间的思考学习，总结了球面上任意两点间距离的计算方法，效果不错。

现介绍如下，以供大家参考。

1.公式推导球面距离，就是球面上经过这两点的大圆的劣弧的长度。

而地球表球面上每个地点的位置是由经度、纬度来确定的，如果能利用经纬度来计算球面距离，我们就可以确定任意两地间的球面距离（不考虑地形影响，下同）。

如左图：设m（w1，j1）、l（w2，j2）为地球表面两点，n为极点，表示两点之间的最短距离（球面距离），、分别表示极点至m、l的经线长。

依球面三角形概念可知：n、m、l共三点构成了球面三角形nml的三个顶点，、、构成了球面三角形的三条边。

它们的夹角、弧度、弧长等可根据球面三角形的性质进行相关计算得出。

为方便计算，按经纬度划分原则，将东经记为正，西经记为负；北纬记为正，南纬记为负。

例；东经60度记作j= +600、西经60度记作j =-600、北纬60度记作w=+600、南纬60度记作w=-600；用a、b、c分别表示三条边、、所对应的球心角，w1 w2分别m、l纬度,j1j2分别表示m、l两地的经度，a表示两地所在经线的夹角且小于1800， r为地球半径。

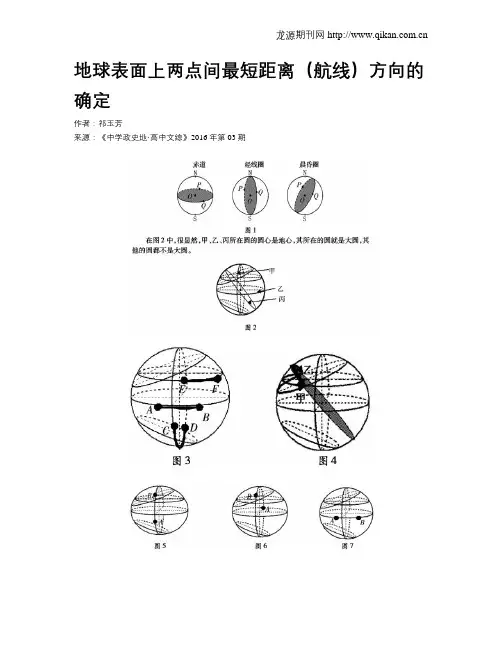
地球表面上两点间最短距离（航线）方向的确定作者：***来源：《中学政史地·高中文综》2016年第03期在复习经纬网的内容时，地球表面上两点间最短航线方向的确定，是我们的拦路虎。

由于有的同学对这类问题缺乏足够的空间想象能力，只是机械地背一些结论，造成在解这类试题时经常出错。

针对有些同学空间想象能力和数学水平不太高等情况，本文旨在帮助他们全面正确认识地球表面上两点间最短航线方向的确定问题。

地球表面上两点之间的最短航线，指的是两点所在大圆的劣弧。

一、认识大圆过球面上两点的大圆就是经过这两点以地心为圆心的圆。

在地球上有三种情况大圆是确定的，如图1中的赤道、经线圈、晨昏圈。

在图2中，很显然，甲、乙、丙所在圆的圆心是地心，其所在的圆就是大圆，其他的圆都不是大圆。

二、确定劣弧大圆上两点间的最短航线或距离就是两点所在大圆的劣弧。

所谓劣弧，即两点间的弧度小于180°。

如图3中的⌒AB和⌒CD都是过大圆的劣弧，而⌒EF虽然是劣弧，但不是大圆上的劣弧。

图4中甲和乙之间的弧线，只有最上面的弧是过大圆的劣弧。

三、确定地球上两点间最短航线的方向沿着劣弧的行进方向就是最短航线的方向。

1.两点在同一经线圈上或者在赤道上（1）两点在同一经线上，向正北或向正南走，不转向。

如图5， A到B是向正北走；反之，B到A是向正南走。

（2）两点在两条经线上（经度相对，两点的经度差等于180°），过极点要转向。

如在通过北极点之前，先向正北走，过北极点后转向正南；反之，在通过南极点之前，先向正南走，过南极点后转向正北。

如图6，从A到B先向正北走，过北极点后向正南走；从B 到A是先向正北走，过北极点后向正南走。

（3）两点在赤道上，向正东走或向正西走，不转向。

如图7， A到B是向正东走；反之，B到A是向正西走。

2.两点既不在同一经线上，也不在赤道上地球上任意两点和地心必然确定一个大圆，一定存在一个纬线圈和这个大圆相切，切点即为这个大圆的纬度最高点，若大圆劣弧航线经过切点，则发生转向，转向点为切点；若大圆劣弧航线不经过切点，则不发生转向。

根据经纬度确定地球上两点之间的最短路程王伟民(安徽省太和县宫集镇中心学校ꎬ安徽阜阳２３６６５２)摘㊀要:以例举的方式ꎬ分三种情况分别介绍如何根据地球表面两点的经纬度ꎬ确定两点之间的最短路程ꎬ以及最短路径长度的计算方法.关键词:地球表面ꎻ经线ꎻ纬线ꎻ最短路径ꎻ圆弧长度中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２３)１３－０１３１－０３收稿日期:２０２３－０２－０５作者简介:王伟民(１９６４－)ꎬ男ꎬ本科ꎬ中学高级教师ꎬ从事高中物理教学研究.㊀㊀由于球体的表面是曲面不是平面ꎬ所以ꎬ沿地球表面运行质点的运动轨迹一定是曲线ꎬ而非直线.运用数学知识可以证明ꎬ在球面上连接任意两点的所有曲线中ꎬ过这两点及球面球心的平面与球面的交线(是一个半径等于球面半径的圆)上ꎬ这两点之间的圆弧(劣弧)的长度最短.运用这一结论ꎬ对于地球表面上给定的两点ꎬ在已知它们经度和纬度的情况下ꎬ依地球半径作为已知条件ꎬ利用数学知识可以确定两地间最短路径的长度.１同一经线上两点之间的最短路程例１㊀已知地球的半径为６４００ｋｍꎬＥ㊁Ｆ是地球表面上的两点ꎬ其经纬度坐标分别为Ｅ(２０ʎＷꎬ５０ʎＮ)㊁Ｆ(２０ʎＷꎬ４０ʎＳ)ꎬ求地球表面上这两点间最短路径的长度.分析㊀依题意可知ꎬＥ㊁Ｆ两点在同一条经线上ꎬ由于经线所在圆的圆心就是地球的球心ꎬ所以ꎬ地球表面上同一经线上两点间的最短路程ꎬ等于这两点之间的经线圆弧的长度.解析㊀设地球的半径为Ｒꎬ球心为点ＯꎬＥ㊁Ｆ两点间的经线圆弧的长度为ｌꎬ则有ｌ＝ＲøＥＯＦ(øＥＯＦ单位为弧度)＝６.４ˑ１０３ｋｍˑ５０ʎ＋４０ʎ１８０ʎπʈ１００５３ｋｍ答:地球表面上这两点间最短路径的长度为１００５３ｋｍ.㊀２同一纬线上两点之间的最短路程需要说明的是ꎬ如果两点在同一条纬线上(即一个点在另一个点的正东或正西方向)ꎬ且这条纬线不是赤道的话ꎬ它们之间的最短路径不是经过这两点纬线圆弧的长度(相当一部分人有这种错误观点ꎬ认为地球表面上东西方向上两点之间最短路径的长度ꎬ等于这两点之间纬线圆弧的长度).例题２㊀已知地球的半径为６４００ｋｍꎬＥ㊁Ｆ是地球表面上的两点ꎬ其经纬度坐标分别为Ｅ(２０ʎＷꎬ６０ʎＮ)㊁Ｆ(８０ʎＷꎬ６０ʎＮ)ꎬ求地球表面上这两点间最短路径的长度分析㊀如图１所示ꎬ设Ｏ是地球球心ꎬ直线ＯＤ是地球的地轴(Ｄ为北极极点)ꎬ圆弧ＡＢ所在的圆是地球的赤道ꎬ圆弧ＥＦ所在的圆是纬度为β＝π３的１３１一条纬线(即øＢＯＦ＝β＝π３)ꎬ圆弧ＡＤ㊁ＢＤ是分别经过Ｅ㊁Ｆ两点且经度相差α＝π３的两条经线(即øＡＯＢ＝α＝π３)ꎬ为确定球面上Ｅ㊁Ｆ两点之间的最短路程ꎬ只需求出线段ＥＦ(是球面的一条弦ꎬ图中未画出)对球心Ｏ点所张的角øＥＯＦ的角度大小即可.图１解析㊀由图１可知øＥＣＦ＝øＡＯＢ＝α＝π３ＣＦ＝ＣＥ＝ＲｃｏｓβＥＦ＝２ＣＦｓｉｎα２＝２Ｒｃｏｓβｓｉｎα２øＥＯＦ＝２ａｒｃｓｉｎ１２ＥＦＯＦ＝２ａｒｃｓｉｎＲｃｏｓβｓｉｎα２Ｒ＝２ａｒｃｓｉｎ(ｃｏｓβｓｉｎα２)＝２ａｒｃｓｉｎ１４所以ꎬ球面上Ｅ到Ｆ的最短路径的长度是以地球半径Ｒ为半径ꎬ弧度大小为２ａｒｃｓｉｎ１４的圆心角所对的弧长ꎬ大小为２Ｒａｒｃｓｉｎ１４.２Ｒａｒｃｓｉｎ１４＝２ˑ６.４ˑ１０３ｋｍˑａｒｃｓｉｎ１４ʈ３２３６ｋｍꎬ答:地球表面上这两点间的最短路径的长度是３２３６ｋｍ.我们将这一数据与过ＥＦ两点纬线上ꎬ圆弧ＥＦ的长度相比较ꎬ设该圆弧长度为ｌꎬ则ｌ＝ＣＦ øＥＣＦ＝(Ｒｃｏｓβ)π３＝π６ˑ６.４ˑ１０３ｋｍʈ３４５０ｋｍ可以看出ꎬ纬线上ＥＦ两点间的圆弧长度比球面上经过ＥＦ的最大圆的圆弧长度多出了１１４ｋｍ.３地球表面任意两点间的最短路程例题３㊀如图２所示ꎬ已知地球的半径为６４００ｋｍꎬＥ㊁Ｆ是地球表面上的两点ꎬ其经纬度坐标分别为Ｅ(２０ʎＷꎬ１５ʎＳ)㊁Ｆ(８０ʎＷꎬ７５ʎＮ)ꎬ求地球表面上这两点之间最短路径的长度.分析㊀由题目条件可知ꎬＥ㊁Ｆ两点既不在同一条经线上ꎬ也不在同一条纬线上.参照上面两例题的解法ꎬ我们只需确定Ｅ㊁Ｆ两点所对地球球心圆心角的大小即可.解析㊀如图２所示ꎬ分别作出过Ｅ㊁Ｆ两点的地球的经线和纬线ꎬ并作出赤道平面.设øＥＡＣ＝α(两条经线的经度之差)ꎬ半径ＯＣ㊁ＯＦ与赤道平面的夹角分别是β和θꎬ由题目条件可知øＥＡＣ＝α＝６０ʎꎬβ＝１５ʎꎬθ＝７５ʎꎬ则:ＡＥ＝ＡＣ＝ＲｃｏｓβＢＤ＝ＢＦ＝ＲｃｏｓθʑＥＣ＝２ＡＣｓｉｎα２＝２Ｒｃｏｓβｓｉｎα２ＤＦ＝２ＢＦｓｉｎα２＝２Ｒｃｏｓθｓｉｎα２ＥＤ＝ＣＦ＝２Ｒｓｉｎβ＋θ２图２㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀图３将图２中的等腰梯形ＥＣＦＤ隔离出来单独分析ꎬ如图３所示ꎬ过其顶点Ｄ㊁Ｆ作该梯形的两条高线ＤＰ和ＦＱꎬ垂足分别为Ｐ㊁Ｑꎬ由勾股定理可知２３１ＥＦ２－ＣＦ２＝ＥＱ２－ＱＣ２ʑＥＦ＝ＣＦ２＋(ＥＱ＋ＱＣ)(ＥＱ－ＱＣ)＝ＣＦ２＋ＥＣ ＤＦ＝４Ｒ２ｓｉｎ２β＋θ２＋４Ｒ２ｃｏｓβｃｏｓθｓｉｎ２α２＝２Ｒｓｉｎ２β＋θ２＋ｃｏｓβｃｏｓθｓｉｎ２α２所以ꎬ图２中ꎬøＥＯＦ的大小(单位为弧度)为øＥＯＦ＝２ａｒｃｓｉｎ１２ＥＦＲ＝２ａｒｃｓｉｎｓｉｎ２β＋θ２＋ｃｏｓβｃｏｓθｓｉｎ２α２所以ꎬ地球表面ꎬＥ㊁Ｆ两点之间的最短路径的的长度ｌ为ｌ＝Ｒ øＥＯＦ＝２Ｒａｒｃｓｉｎｓｉｎ２β＋θ２＋ｃｏｓβｃｏｓθｓｉｎ２α２＝２Ｒａｒｃｓｉｎ１２＋２＋３２＋６１２＋６１４＝２Ｒａｒｃｓｉｎ３４＝２ˑ６.４ˑ１０３ｋｍ ａｒｃｓｉｎ３４ʈ１０８５５ｋｍ答:地球表面上这两点间的最短路径的长度是１０８５５ｋｍ.例３解答中ꎬ所导出的根据地球表面两点的经纬度确定两点之间最短路径长度的计算公式ｌ＝２Ｒａｒｃｓｉｎｓｉｎ２β＋θ２＋ｃｏｓβｃｏｓθｓｉｎ２α２ꎬ是一个普遍适用的公式ꎬ它涵盖了已知两点在同一条经线㊁同一条纬线ꎬ以及已知两点既不在同一条经线也不在同一条纬线等多种情形.该公式中ꎬ当β＝－θ时ꎬ公式演变为ｌ＝２Ｒａｒｃｓｉｎ(ｃｏｓβｓｉｎα２)ꎬ这就是例２中ＥＦ两点在同一条纬线上的情形.当α＝０时ꎬｌ＝２Ｒａｒｃｓｉｎｓｉｎ２β＋θ２＋ｃｏｓβｃｏｓθｓｉｎ２α２＝２Ｒａｒｃｓｉｎ(ｓｉｎβ＋θ２)＝２Ｒａｒｃｓｉｎ(ｓｉｎβ＋θ２)＝Ｒ(β＋θ)ꎬ这正是例１中两点在同一条经线的状况.看该公式的一个实际应用.例４㊀已知北京和悉尼两座城市的经纬度坐标分别如下:北京(１１６.４６ʎＥꎬ３９.２ʎＮ)㊁悉尼(１５０.８８ʎＥꎬ３３.９２ʎＳ)ꎬ试求北京和悉尼间最短航线的长度(地球半径取６４００ｋｍ).解析㊀依题意知ꎬα＝１５０.８８ʎ－１１６.４６ʎ＝３４.４２ʎꎬβ＝３３.９２ʎꎬθ＝３９.２ʎ所以ꎬ两城市间的最短航线长度ｌ为ｌ＝２Ｒａｒｃｓｉｎｓｉｎ２β＋θ２＋ｃｏｓβｃｏｓθｓｉｎ２α２＝２Ｒａｒｃｓｉｎｓｉｎ２３６.５６ʎ＋ｃｏｓ３３.９２ʎｃｏｓ３９.２ʎｓｉｎ２１７.２１ʎʈ８２００ｋｍ答:北京和悉尼间最短航线的长度约为８２００ｋｍ.当然ꎬ这里计算出的数据只是理论数据ꎬ两地间的实际航线还要受地理环境等多种因素的影响ꎬ飞机的实际飞行路线很可能会偏离 标准 的圆弧线ꎬ中途出现 拐弯 的情形ꎬ所以实际航线的长度会比理论值大一些.参考文献:[１]陈龙.追溯 源头 拨开云雾见 真身 :例析 与圆相关的最值问题 [Ｊ].数理化解题研究ꎬ２０２２(６):８４－８６.[２]许婷婷.例谈立体图形表面最短距离[Ｊ].高中数理化ꎬ２０１９(１０):１６－１７.[３]牛可新.巧解 求曲线上的点到直线的最短距离 题[Ｊ].数学学习与研究ꎬ２０１３(９):９９.[责任编辑:李㊀璟]３３１。