两点间的距离及点到直线的距离

极坐标下两点间的距离公式、点到直线间的距离公式及其应用人教A 版选修4-4中极坐标部分内容有好多求极坐标下两点间的距离和点到直线的距离的问题，我们一般都是把点极坐标与直线的极坐标方程化为直角坐标和方程，然后利用直角坐标下的公式来解决的。

那么，能不能直接利用极坐标来解决这两个问题呢？答案是肯定的。

下面我们分别来说明。

一.极坐标下两点间的距离公式及其应用1.结论一：设两点的极坐标分别是A （ρ1，θ1）、B （ρ2，θ2），则221212212cos -AB ρρρρθθ=+-（）证明：如图，设两点的极坐标分别是A （ρ1，θ1）、B （ρ2，θ2），且ρ1>0,ρ2>0在△AOB 中，由余弦定理，得222cos AB OA OB OA OB AOB =+-∠221212212cos -ρρρρθθ=+-（）说明：也可以把点的极坐标化为直角坐标，用直角坐标下两点间的距离公式得证。

2.应用例1.在极坐标系中，已知A ⎝⎛⎭⎪⎫1，3π4，B ⎝ ⎛⎭⎪⎫2，π4两点，则|AB |＝________. 解：|AB |＝12＋22－2×1×2co s ⎝ ⎛⎭⎪⎫3π4－π4＝ 5. 例2.求圆心在C ⎝⎛⎭⎪⎫2，π4，半径为1的圆的极坐标方程． 解：设圆C 上任意一点的极坐标为M (ρ，θ)，如图，在△OCM 中，得|OM |2＋|OC |2－2|OM |·|OC |·cos∠COM ＝|CM |2，即ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＋1＝0. 当O ，C ，M 三点共线时，点M 的极坐标⎝⎛⎭⎪⎫2±1，π4也适合上式， 所以圆的极坐标方程为ρ2－22ρcos ⎝ ⎛⎭⎪⎫θ－π4＋1＝0. 二.极坐标下点到直线的距离公式及其应用1.结论二:在极坐标系中，设()11,p ρθ ，直线l 方程为22sin()a ρθϕ=+ 则点P 到直线l 的距离为112sin()-d a ρθθ=-证明:将()11,p ρθ化成直角坐标为1111(cos ,sin )ρθρθ 由直线l 方程222(sin cos cos sin )a ρθϕθϕ+=即2222sin cos cos sin a ρθϕρθϕ+=化成直角坐标系由点到直线的距离公式，可得sin cos 0x y a ϕϕ+-= 111122cos sin sin cos cos sin ad ρθϕρθϕϕϕ+-=+11sin()a ρθϕ=+- 2.应用:例1.已知直线的极坐标方程为2sin()4ρθ+=π 7(2,)4A π到这条直线的距离。

《两点间的距离及点到直线的距离》课标分析
新课程标准要求教师在教学中培养学生初步学会从数学的角度发现问题和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力。

能探索分析和解决简单问题的有效方法，了解解决问题方法的多样性。

在从事与他人合作解决问题的活动，尝试解释自己的思考过程。

能初步判断结果的合理性，经历整理解决问题过程和结果的活动。

学会独立思考，体会数学的基本思想和思维方式。

在运用数学解决问题的过程中，认识数学的价值。

主动参与数学学习活动以及在他人的鼓励和引导下，体验克服困难、解决问题的过程，相信自己能够学好数学。

初步养成乐于思考、勇于质疑、实事求是等良好品质。

课表明确要求：经历图形的抽象、分类、性质探讨、运动、位置确定等过程，掌握图形与几何的基础知识和基本技能。

建立符号意识和空间观念，初步形成几何直观能力，发展形象思维与抽象思维。

探索一些图形的形状、大小和位置关系，了解一些几何体和平面图形的基本特征，掌握测量、识图和画图的基本方法。

体会两点间所有连线中线段最短，知道两点间的距离。

根据两点间的距离及点到直线的距离教学内容把知识目标定位为结合具体情景，理解“两点间所有连线中线段最短”，知道两点间的距离和点到直线的距离。

能力目标定位为对两点间的距离和点到直线的距离知识的探究过程中，培养观察、想象、动手操作的能力，发展初步的空间观念。

情感态度价值观目标定位为在解决实际问题的过程中，体验数学与日常生活的密切联系，提高学习兴趣，学会与他人合作共同解决问题。

第四单元
两点间的距离及点到 直线的距离
回顾复习
• 1、同一平面内的两条直线的位置关系有 （ 平行）和（相交） 2、一条直线的平行线有（无数）条 3、两条直线的交点叫做 （垂足 ） 4、在（同一平面 ）内不相交的两条直线叫做 平行线，也可以说这两条直线（互相平行 ）
认一认：
下面各组直线，哪组相交，哪组互相平行？ 互相垂直?
①
②
③
④
⑤
⑥
垂直
垂直
你能过直线外一点画 这条直线的垂线吗？
一.线边重合 二.平移靠点
三. 画线 四. 标符号
你能过直线外一点画 这条直线的垂线吗？
点到直线的距离： 从直 线外一点到这条直线所画 的垂直线段的长度，叫作 点到直线的距离
两点间的距离问题
有只虫子从一个山洞到另一个山洞寻找食物, 有五条路可走,可是走哪一条路最短呢?可怜的 小虫子犯愁了,谁能帮帮它呢? 1 2 3 起点 终点 4 5
A
路
公
B
能力提升：
a、平行线间的距离处处相等 b两条直线互相平行， a、b两直线间的线 平行线间垂直线段的长度 段中那条最短？ 就是平行线间的距离
这节课
你有什么收获？
作业
• 优＋学案中相关的课时做完
线段最短!
大青虫家门前有条大路，它要到路上去，怎么走最近呢?
两点之间线段最短，两 点之间线段的长度就是 两点间的距离。
点到直线所 画的垂直线 段最短
点到直线的距离问题
公路
从直线外一点到这条直线所画的 垂直线段 这条线路与公路垂直! 最短，它的长度叫做 这点到直线的距离。
？
小结：
• 1、两点之间线段的长度就是两点间的距离。 • 2、从直线外一点到这条直线所画的垂直线段最短， 它的长度叫作点到直线的距离 • 3、两点之间线段最短，点到直线所画的垂直线段 最短 • 4、从直线外一点到已知直线，可以画无数条线段， 可以画一条垂直线段

教案标题：三年级下册数学教案-7 两点之间的距离及点到直线的距离-青岛版（五四学制）一、教学目标1. 让学生理解并掌握两点之间的距离及点到直线的距离的计算方法。

2. 培养学生的空间想象能力和抽象思维能力。

3. 培养学生运用数学知识解决实际问题的能力。

二、教学内容1. 两点之间的距离2. 点到直线的距离三、教学重点与难点1. 教学重点：两点之间的距离及点到直线的距离的计算方法。

2. 教学难点：如何引导学生理解并运用这些计算方法。

四、教学过程1. 导入在黑板上画出两个点A和B，让学生思考如何计算点A和点B之间的距离。

引导学生回顾已学的长度单位，如厘米、米等，并提示学生可以使用直尺来测量两点之间的距离。

2. 新课导入介绍两点之间的距离的概念，并给出计算公式：两点之间的距离等于两点间的直线距离。

用具体的例子进行演示，如点A(2,3)和点B(5,7)，计算它们之间的距离。

3. 活动一：计算两点之间的距离让学生分组，每组发一张坐标纸和几个点，让学生自己在坐标纸上画出几个点，并用直尺测量它们之间的距离。

然后，让学生计算这些距离，并核对自己的测量结果。

4. 活动二：点到直线的距离引导学生思考如何计算一个点到一条直线的距离。

首先，让学生画出一条直线和一点，然后用直尺测量这个点到直线的最短距离。

接着，给出点到直线的距离的计算公式：点到直线的距离等于点到直线的垂线的长度。

5. 活动三：应用出示一些实际问题，如计算点到直线的距离、计算两点之间的距离等，让学生运用所学的知识来解决这些问题。

6. 总结对本节课所学的内容进行总结，强调两点之间的距离和点到直线的距离的计算方法，并提醒学生在解决实际问题时要注意单位的转换。

五、作业布置1. 让学生完成课后练习题。

2. 让学生回家后，观察身边的物体，尝试计算两个物体之间的距离。

六、教学反思1. 在教学过程中，要注意引导学生运用数学知识解决实际问题，培养学生的实际操作能力。

2. 在讲解点到直线的距离的计算方法时，可以结合具体的例子进行讲解，帮助学生理解。

教学内容：两点间的距离及点到直线间的距离第三课时教学目标1.通过“猜一猜，画一画，量一量”活动，理解体会“两点之间线段最短”、“点到直线所画的垂线段最短”，知道两点间的距离和点到直线的距离的含义。

2.在探究知识的过程中经历“猜想—验证”的探究过程，培养观察、想象、动手操作的能力，发展初步的空间观念。

3.在解决实际问题的过程中，体验数学与日常生活的密切联系，提高学习兴趣，培养学生的应用意识。

教学重点结合具体情境理解体会“两点之间线段最短”、“点到直线的垂直线段最短”。

教学难点理解“点到直线的距离”及其画法。

教学准备：教师准备：多媒体课件、作业纸；学生准备：直尺、三角板、毛线教学过程一、创设情景，提出问题师：同学们，为了交通方便，在修路时遇到河要架桥，如果遇到了大山，应该怎么办呢？图1组织学生发表自己的意见。

预设1：绕过山。

预设2：火车爬山。

预设3：修建隧道。

引导学生讨论总结：绕路需要多费时间、费能源。

火车爬山也不太安全，直接通过隧道方法好像更好一些。

（课件出示，见图1）看图，教师向学生讲解什么是隧道：隧道是埋置于底层内的一种地下建筑物。

隧道可分为山岭隧道、水底隧道和地下隧道等。

师：为什么要修隧道呢？今天这节课就一起研究这其中的秘密。

二、合作探索，解决问题（一）认识两点间的距离1. 提出猜想。

师：刚才同学们都认为修隧道的路程最近，其他的方法路程会远一些，这是生活经验告诉我们的，其实在数学上它还只是一个猜想。

板书：猜想。

2.操作验证。

（1）讨论研究方案。

师：这种观点究竟对不对呢？在我们还需要验证一下。

给学生一个简易的大山图，在山的两侧分别标出两个点A和 B。

师：小组内讨论一下，我们应该怎样做才能证明我们的观点是否正确？小组内讨论制定研究计划。

全班交流研究计划。

课件出示探究方案：①从A 地到 B地，你能把修隧道的方法在图上表示出来吗？动手画一画。

你还能想到哪些不同的路线？试着画几条，看看能发现什么？②利用学具动手摆一摆、比一比、量一量，验证你的发现是否正确。

性和安全性。
Part
05
距离在物理中的应用
重力场中的距离
重力场中两点间的距离
在重力场中，两点间的最短距离是通过连接这两点的直线段来确定的。重力场中的距离与地球的质量和物体的质 量有关。
重力加速度
在重力场中，物体受到地球的引力作用，产生加速度，这个加速度被称为重力加速度。重力加速度的大小与地球 的质量和物体的高度有关。
点到直线的距离
点到直线的距离是指点到直线上的任意一点的最短距离。在确定一个点相对于一条直线 的位置时，这个距离是非常重要的。
图形分析
三角形分析
在三角形中，通过测量各边和各边之间的距离，可以分析三角形的形状和大小。 例如，海伦公式用于计算三角形的面积。
圆的分析
在圆中，通过测量圆心到圆上任一点的距离（半径），可以分析圆的大小和位 置。此外，圆上两点间的最大和最小距离分别是直径和弦。
举例说明
假设在二维平面中，点A的坐标为(0, 0)，点B的坐标为(4, 3)，则两点间的距离为：d = sqrt(4^2 + 3^2) = 5。
假设在三维空间中，点A的坐标为(0, 0, 0)，点B的坐标为(4, 3, 6)，则两点间的距离为： d = sqrt(4^2 + 3^2 + 6^2) = 7。
Part
03
距离的性质
非负性
STEP 01
STEP 02
STEP 03
这一性质是距离定义的基 本要求，确保了距离的度 量具有实际意义。
当且仅当两点重合时，距 离d为0。
两点间的距离总是非负的， 即两点间的距离d满足d ≥ 0。
三角不等式
对于任意三点A、B、 C，有AB ≤ AC + CB。

平面上两点间的距离和点到直线的距离公式平面几何是几何学中的一个重要分支，它研究了平面上点、直线、圆等的性质和相互关系。

在平面上，我们经常需要计算两点之间的距离以及点到直线的距离，这些计算方法在实际生活中有着很广泛的应用。

下面我们将分别介绍两点间的距离和点到直线的距离的计算公式。

首先，考虑两点间的距离。

假设平面上有两个点A(x1,y1)和B(x2,y2)，我们想要计算这两个点之间的距离d。

根据勾股定理，我们知道两点之间的距离可以通过点与坐标轴的距离的平方和来计算，即：d=√[(x2-x1)^2+(y2-y1)^2]。

这个公式的理解非常直观，我们可以将两点之间的直线看作是直角三角形的斜边，而点与坐标轴的距离就是直角三角形的两个直角边的长度。

因此，我们可以通过计算两个直角边的长度，然后应用勾股定理来求解斜边的长度，即两点之间的距离。

接下来，我们来讨论点到直线的距离的计算方法。

给定平面上一条直线L和一点C(x0,y0)，我们想要计算点C到直线L的距离d。

为了方便计算，我们需要确定直线L的方程。

在平面几何中，常见的直线方程形式有一般式、斜截式和点斜式。

这里我们以一般式方程为例，一般式方程的形式为Ax+By+C=0，其中A、B和C是常数。

点到直线的距离的计算方法有多种，下面我们介绍其中的一种方法，即点到直线的投影方法。

我们可以将问题转化为求点C到直线L的垂直投影点D，然后计算点C到点D的距离d。

首先，我们可以利用点斜式确定直线L的斜率k。

假设直线L经过点P(x1, y1)，斜率为k，则直线L的点斜式方程为y - y1 = k(x - x1)。

进一步化简，我们得到直线L的一般式方程Ax + By + C = 0，其中A =-k，B = 1，C = kx1 - y1接下来，我们需要求点C到直线L的垂直投影点D(xd, yd)的坐标。

根据垂直投影的性质，我们知道点D在直线L上，且点CD垂直于直线L。

因此，点D与直线L的斜率之积为-1，即k * kd = -1、由此，我们可以得到点D的坐标：xd = (B^2 * x0 - A * B * y0 - A * C) / (A^2 + B^2)yd = (A * B * x0 - A * A * y0 - B * C) / (A^2 + B^2)最后，我们可以计算点C到点D的距离d，即：d = √[(x0 - xd)^2 + (y0 - yd)^2]这个公式可以通过将点C到点D的距离看作直角三角形的斜边来进行解释。

B1 B2
y y
C1 C2
0 0
点A
A坐标(a,b)
直线L
L方程：Ax+By+C=0
点A在L上 直线L1∩L2=A
aA1 bB1 C1 0
A1 A2
x x
B1 B2
y y
C1 C2
0 0
x y
a b
直线上的点
y
l
2x y 3 0
P(x,y) x
(1)点（1，5）在直线上吗？ (2)点（2，7）在直线上吗？
A(0,0) B(a,0)
| AC |2 | BD |2 2(a2 b2 c2 )
| AB |2 | BC |2 | CD |2 | AD |2 2(a2 b2 c2 )
结 论 L：3x=2的距离。
解1 : d | 3 (1) 0 2 | 5
|PA|的值。
解: 设P( x,0),则
| PA | ( x 1)2 (0 2)2 x2 2 x 5
| PB | ( x 2)2 (0 7 )2 | PA || PB |
x2 2 x 5 x2 4 x 11 解得: x 1, P(1,0)
x2 4 x 11
| PA | (1 1)2 (0 2)2 2 2
由2x 3 y 1 0令x 0得y 1 ; y 0得x 1
3
2
直线与x轴交于A( 1 ,0),与y轴交于B(0, 1 ).
2
3
L过A关于y轴对称点( 1 ,0)和B点, L方程为
2
x 1
y 1
1即: 2x 3 y 1
0
23
2、已知L的方程：2x+3y+1=；则
（1）将L向上平移2个单位得：_________

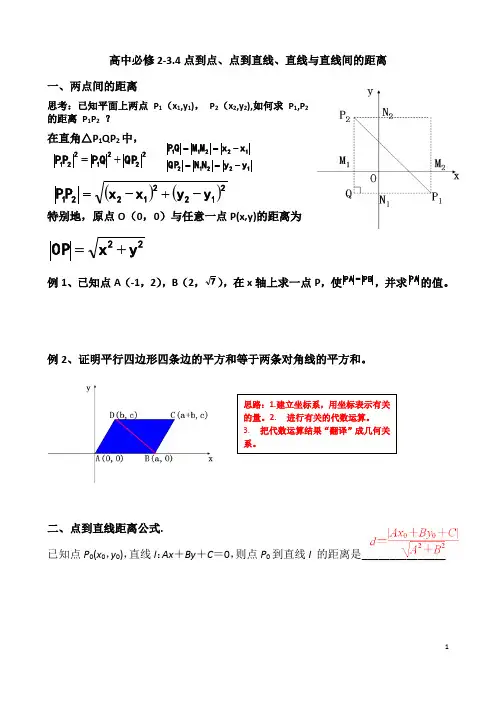
高中必修2-3.4点到点、点到直线、直线与直线间的距离一、两点间的距离思考：已知平面上两点P 1（x 1,y 1)， P 2（x 2,y 2),如何求P 1,P 2的距离 P 1P 2 ？在直角△P 1QP 2中，特别地，原点O （0，0）与任意一点P(x,y)的距离为22y x OP +=例1、已知点A （-1，2），B （2，7），在x 轴上求一点P ，使PB PA =，并求PA 的值。

例2、证明平行四边形四条边的平方和等于两条对角线的平方和。

二、点到直线距离公式.已知点P 0(x 0，y 0)，直线l ：Ax ＋By ＋C ＝0，则点P 0到直线l 的距离是_______________.2221221QP Q P P P +=1221212211y y N N QP x x M M Q P -==-==()()21221221y y x xP P -+-=结论：点P 0(x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离为：例1 求点P(-1,2)到直线①2x+y -10=0； ②3x=2的距离。

解： ①根据点到直线的距离公式，得()521210211222=+-⨯+-⨯=d②如图，直线3x=2平行于y 轴，35)1(32=--=∴d小结：1.点到直线距离公式 注意： 化为一般式．2.特殊情况三、两平行线间距离公式.2.两条平行线Ax+By+C 1=0与Ax+By+C 2=0的距离是取直线Ax+By+C 1=0上一点P 0(x 0，y 0)，当x= x 0时，y 0=-0B ，即点P 0坐标为： P 0(x 0，-AX 0+CB)， P 0到直线Ax+By+C 2=0的距离是例2 求平行线2x -7y+8=0与2x -7y-6=0的距离。

分析：直线到直线的距离转化为点到直线的距离课后高频考点练习直线的交点坐标与距离公式高频考点练习题（人教A版）一、单选题(共12道，每道8分)1.已知点A(2，m)与点B(m，1)之间的距离等于，则实数m的值为( )A.-1B.4C.-1或4D.-4或12.已知点A(-1，2)，点B(2，)，点P在x轴上，使，则点P坐标是( )A.(2，0)B.(-2，0)C.(1，0)D.(-1，0)3.过和的交点且与平行的直线是( )A. B. C. D.4.若直线经过直线和的交点，且垂直于直线，则直线的方程为( )A. B. C. D.5.已知点M(2，-3)，N(-3，-2)，直线与线段MN相交，则实数a的取值范围是( )A. B. C. D.6.无论m取何实数，直线恒过定点( )A.(2，3)B.(1，3)C.(2，4)D.(3，4)7.若M(2，3)，N(4，-5)，直线过P(1，2)，且点M，N到直线的距离相等，则直线的方程为( )A. B. C.D.8.两平行直线与之间的距离为( )A. B. C.1 D.9.与直线的距离为的直线的方程是( )A. B. C. D.10.到两直线和的距离相等的点P(x，y)满足的方程是( )A. B. C. D.11.已知两条平行直线，，则到直线的距离与到直线的距离之比是3：2的直线方程是( )A. B.C. D.12.已知，，则S的最小值是( )A.0B.2C.4D.参考答案：1.解题思路：试题难度：三颗星知识点：两点间距离公式的应用2.解题思路：试题难度：三颗星知识点：两点间距离公式的应用3. 解题思路：试题难度：三颗星知识点：两条直线的交点坐标4.解题思路：试题难度：三颗星知识点：两条直线的交点坐标5.解题思路：试题难度：三颗星知识点：恒过定点的直线6.解题思路：试题难度：三颗星知识点：恒过定点的直线7.解题思路：试题难度：三颗星知识点：点到直线的距离公式8. 解题思路：试题难度：三颗星知识点：两条平行直线间的距离9. 解题思路：试题难度：三颗星知识点：两条平行直线间的距离10.解题思路：试题难度：三颗星知识点：两条平行直线间的距离11.解题思路：试题难度：三颗星知识点：两条平行直线间的距离12.解题思路：试题难度：三颗星知识点：两点间距离公式的应用。

2
D(b,c) C(a+b,c)
| AC | (a b ) c
2 2
| BD |2 (b a ) 2 c 2
2 2
A(0,0) B(a,0)
2
| AC | | BD | 2(a b c ) | AB |2 | BC |2 | CD |2 | AD |2 2(a 2 b 2 c 2 ) 结论成立 .
(3)点（3， 8）在直线上吗？
直线的方程就是直线上每一 点坐标满足的一个关系式.
例1、求下列直线的交点坐标：
l1 : 3 x 4 y 2 0 l2 : 2 x y 2 0
3 x 4 y 2 0 x 2 解 : 解方程组 2 x y 2 0 y 2 所以 l1与l 2交点为 ( 2,2)
2 2
x 2x 5
2
| PB | ( x 2) 2 (0 7 ) 2 | PA || PB | 2 2 x 2 x 5 x 4 x 11 解得 : x 1, P (1,0) | PA | (1 1) (0 2) 2 22ຫໍສະໝຸດ 2一、两直线的交点(坐标):
已知直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0, 则l1与l2的交点P坐标(x,y)就是方程组的解:
A1 x B1 y C1 0 A x B y C 0 2 2 2
点A 直线L 点A在L上 直线L1∩L2=A A坐标(a,b) L方程：Ax+By+C=0
aA1 bB1 C1 0 A1 x B1 y C1 0 x a A x B y C 0 y b 2 2 2

AB ( x1 x2 )2 ( y1 y2 )2 ( z1 z2 )2
3.求点到平面的距离:如图点P为平面外一点， 点A为平面内的任一点，平面的法向量为n,过 点P作平面的垂线PO，记PA和平面所成的 角为，则点P到平面的距离 n
P
d PO PA sin
1
A
这个晶体的对角线 AC1 的长是棱长的
6倍。
思考： (1)本题中四棱柱的对角线BD1的长与棱长有什么关系？
(2)如果一个四棱柱的各条棱长都相等，并且以 某一顶点为端点的各棱间的夹角都等于 , 那么 有这个四棱柱的对角线的长可以确定棱长吗?
A1 B1 D C
D1
C1Βιβλιοθήκη (3)本题的晶体中相对的两个平面之间的距离 A B 是多少? (提示：求两个平行平面的距离，通常归结为求点到平 面的距离或两点间的距离）
补充作业：
已知正方形ABCD的边长为4，CG⊥平面 ABCD，CG=2,E、F分别是AB、AD的中点， z G 求点B到平面GEF的距离。
x
F
D
C
A
E
B
y
4.异面直线的距离:
①作直线a、b的方向向量a、 b，求a、b的法向量n，即此 异面直线a、b的公垂线的方 向向量； ②在直线a、b上各取一点 A、B，作向量AB； ③求向量AB在n上的射影 d，则异面直线a、b间的距 离为
1 解:∵ D1 (0, 0,1), B(1,1, 0), A1 (1, 0,1), E (0, ,1) 2 1 A1 E 1, , 0 , D1B 1,1, 1 2 设 n ( x , y , z )是与 A1 E , D1 B都垂直的向量， A1 1 则 n A E 0, 1 x y 0, y 2 x , 2 即 z 3 x, n D1 B 0, x y z 0, 取x＝1，得其中一个n (1, 2, 3) A 选A1 E与BD1的两点向量为 D1 A1 1, 0, 0 , D1 A1 n 14 得A1 E与BD1的距离 d 14 n

§3.3.2两点间的距离，点到直线的距离，两平行线间的距离基础知识过关检测姓名 评价1. 两点间的距离两点()111,P x y ,()222,P x y 间的距离12PP =. （1）当直线12PP 平行于轴时,12PP =； （2）当直线12PP 平行于轴时,12PP =；（3）当12,P P 中有一个是原点时,不妨设在原点,则12PP =； （4）当12,P P 在直线y kx b =+上时,12PP =.（1）直线方程应为一般式，若给出其他形式，应先化成一般式再用公式.例如求()00,P x y 到直线y kx b =+的距离，应先把直线方程化为，得d =.（2）点在直线上时，点到直线的距离为零，公式仍然适用，故应用公式时不必判定点与直线的位置关系.（3）直线方程0Ax By C ++=中0A =或0B =时，公式也成立，也可以用下列方法求点到直线的距离.①()00,P x y 到x a =的距离d =； ②()00,P x y 到y b =的距离d =.4.已知ABC ∆的顶点A(2,3),B(-1,0),C(2,0),则ABC ∆的周长是( )A.2B.3+2C.6+3D.6+105.一条线段的长是5个单位，它的一个端点是A （2，1），另一个端点B 的横坐标是-1，则点B 的纵坐标是（ ）A.-3B.5C.-1或-3D.-3或56.若轴上的点M 到原点的距离与到点N （5，-3）的距离相等，则M 点的坐标是（ ）A.（-2，0）B.（1，0）C.（23，0）D.（3.4，0） 7.已知ABC ∆的顶点坐标为A(7,8)、B(10,4)、C(2,-4),则BC 边上的中线AM 的长为_____________. 8.点(2,1)到直线:220l x y -+=的距离为( )A.52B.52C.56D.0 9.已知()(),20a a >到直线:30l x y -+=的距离为1，则的值为（ ）A.-1B.+1C.2-1D.2+110.两条平行线1:3470l x y +-=和2:34120l x y +-=的距离为（ ）A.3B.2C.1D.21 11.分别过点A （-2，1）和点B （3，-5）的两条直线均垂直于轴，则这两条直线的距离为__________.能力提升1. 两平行直线，分别过点P （-1，3），Q （2，-1）它们分别绕P ，Q 旋转，但始终保持平行，则，之间的距离的取值范围是（ ）A ．()0,+∞ B.（0，5） C.(]0,5D.( 2. 点(4cos ,3sin )P θθ到直线60x y +-=的距离的最小值等于.3. 与直线210x y ++=. 4. 过原点且与两定点)2,3(),1,1(--B A 距离相等的直线的方程为. 5. 已知ABC ∆的三个顶点坐标是A （1，-1），B （-1，3），C （3，0）. （1）判定ABC ∆的形状； （2）求ABC ∆的面积.6. 试在直线40x y -+=上求一点，使它到点M （-2，-4）、N （4，6）的距离相等.7. 已知三条直线()1:200l x y a a -+=<2:4210l x y -++=3:10l x y +-= ，若与的距离是（1）求的值；（2）能否找到一点使得同时满足下列三个条件:①是第一象限的点；②点到的距离是点到的距离的12；若能，求点坐标；若不能，说明理由.§3.3.2两点间的距离，点到直线的距离，两平行线间的距离基础知识过关检测姓名 评价1. 两点间的距离两点()111,P x y ,()222,P x y 间的距离12PP =. （1）当直线12PP 平行于轴时,12PP =； （2）当直线12PP 平行于轴时,12PP =；（3）当12,P P 中有一个是原点时,不妨设在原点,则12PP =； （4）当12,P P 在直线y kx b =+上时,12PP =.（1）直线方程应为一般式，若给出其他形式，应先化成一般式再用公式.例如求()00,P x y 到直线y kx b =+的距离，应先把直线方程化为，得d =.（2）点在直线上时，点到直线的距离为零，公式仍然适用，故应用公式时不必判定点与直线的位置关系.（3）直线方程0Ax By C ++=中0A =或0B =时，公式也成立，也可以用下列方法求点到直线的距离.①()00,P x y 到x a =的距离d =； ②()00,P x y 到y b =的距离d =.4.已知ABC ∆的顶点A(2,3),B(-1,0),C(2,0),则ABC ∆的周长是( C )A.2B.3+2C.6+3D.6+105.一条线段的长是5个单位，它的一个端点是A （2，1），另一个端点B 的横坐标是-1，则点B 的纵坐标是（ D ）A.-3B.5C.-1或-3D.-3或56.若轴上的点M 到原点的距离与到点N （5，-3）的距离相等，则M 点的坐标是（ D ）A.（-2，0）B.（1，0）C.（23，0）D.（3.4，0） 7.已知ABC ∆的顶点坐标为A(7,8)、B(10,4)、C(2,-4),则BC 边上的中线AM 的长为_____________. 8.点(2,1)到直线:220l x y -+=的距离为( B )A.52B.52C.56D.0 9.已知()(),20a a >到直线:30l x y -+=的距离为1，则的值为（ A ）A.-1B.+1C.2-1D.2+110.两条平行线1:3470l x y +-=和2:34120l x y +-=的距离为（ C ）A.3B.2C.1D.21 11.分别过点A （-2，1）和点B （3，-5）的两条直线均垂直于轴，则这两条直线的距离为__________.能力提升1. 两平行直线，分别过点P （-1，3），Q （2，-1）它们分别绕P ，Q 旋转，但始终保持平行，则，之间的距离的取值范围是（ ）A ．()0,+∞ B.（0，5） C.(]0,5 D.( 解析:最大值为P ，Q 的距离，即5，选C2. 点(4cos ,3sin )P θθ到直线60x y +-=的距离的最小值等于.解析:222|6)sin(5|2|6sin 3cos 4|≥-+=-+=φθθθd3. 与直线210x y ++=的距离为5.解析:02=+y x 或022=-+y x4. 过原点且与两定点)2,3(),1,1(--B A 距离相等的直线的方程为.解析: 直线过线段AB 的中点或平行于直线AB ，故方程为02=+y x 或043=+y x 5. 已知ABC ∆的三个顶点坐标是A （1，-1），B （-1，3），C （3，0）. （1）判定ABC ∆的形状； （2）求ABC ∆的面积.解：（1）如图，△ABC法一：∵|AB |=[]22)1(3)11(--+--=20=2，|AC |=[]22)1(0)13(--+-=，|BC |=[]22)30()1(3-+--=25=5，∴|AB |2+|AC |2=|BC |2，即△ABC 是以A 为直角顶点的直角三角形. 法二：∵k AB =11)1(3----=-2，k AC =13)1(0--- = 21，∴k AB ·k AC =-1，∴AB ⊥AC ，∴△ABC 是以A 为直角顶点的直角三角形. （2）∵∠A =90°， ∴S △ABC =21|AB |·|AC |=5. 规律方法：判定三角形形状的依据是三角形的分类标准，由边的分类或角的分类进行解决. 6. 试在直线40x y -+=上求一点，使它到点M （-2，-4）、N （4，6）的距离相等. 解：法一：由直线x -y +4=0，得y =x +4，点P 在该直线上. ∴可设P 点的坐标为（a ，a +4）. 由已知|PM |=|PN |， ∴[][]22)4(4)2(--++--a a=22)64()4(-++-a a ,22)8()2(+++a a =22)2()4(-+-a a .∴（a +2）2+（a +8）2=（a -4）2+（a -2）2.解得a =-23，从而a +4=-23+4=25. ∴P （-23，25）.法二：由于|PM |=|PN |，∴点P 在线段MN 的垂直平分线上. 由于k MN =)2(4)4(6----=610=35， ∴线段MN 的垂直平分线的斜率为k =-53. 又MN 的中点为（1，1），∴线段MN 的垂直平分线的方程为y -1=-53（x -1）， 即y =-53x +58. 又∵点P 在直线x -y +4=0上，∴点P 为直线x -y +4=0与y =-53x +58的交点. 由⎪⎩⎪⎨⎧+-==+-,5853,04x y y x得⎪⎪⎩⎪⎪⎨⎧=-=.25,23y x∴点P 的坐标为（-23，25）. 7. 已知三条直线()1:200l x y a a -+=<2:4210l x y -++=3:10l x y +-= ，若与的距离是（1）求的值；（2）能否找到一点使得同时满足下列三个条件:①是第一象限的点；②点到的距离是点到的距离的12；若能，求点坐标；若不能，说明理由.【解题思路】由三个条件可列三个方程或不等式，最终归结为混合组是否有解的问题[解析]（1）21:20,32l x y d a --===⇒=(2)设00(,)P x y 同时满足三个条件 由②得：设00(,)P x y 在':20l x y C -+=131126C C =⇒==或则有00001311202026x y x y -+=-+=或------------（1）=000240320x y x ⇒-+=+=或--------------（2）由①得 000,0x y >> ----------------（3） 解由（1）（2）（3）联立的混合组得 00137,.918x y == 所以137(,)918P 【名师指引】（1）在条件比较多时，思路要理顺；（2）解混合组时，一般是先解方程，再验证不等式成立。

“两点之间的距离与点到直线的距离”》教学设计及教学反思教学内容：青岛版小学数学三年级下册第七单元信息窗3教学目的：1.结合具体情境，理解“两点间所有连线中线段最短”，知道两点间距离和点到直线的距离。

2.在对两点间的距离和点到直线的距离知识的探究过程中，培养观察、想象、动手操作的能力，发展初步的空间观念。

3.在解决实际的问题过程中，体验数学与日常生活的密切联系，提高学习兴趣，学会与他人合作共同解决问题。

教学重点与难点：理解两点间距离和点到直线的距离。

教学准备：三角尺、直尺、多媒体课件、铁丝路线教学过程一、故事引入，激发兴趣1.你们喜欢听故事吗？（喜欢）2.播放故事“蜘蛛与苍蝇”。

【设计意图：俗话说：“善始者，事半成”。

一个妙趣横生、引人入胜的故事引入，促使学生迅速进入了最佳的学习状态，为整节课的教学活动奠定了良好的基础。

】二、学习“两点之间的距离”1.学习“两点之间线段最短”（1）请问：蜘蛛走哪几条路能捉到苍蝇？（学生指一指）我们一起看看这几条重要的路线，黑板出示自制“四条路”的铁丝教具：（2）如果用AB两点分别表示蜘蛛和苍蝇所在的位置，大家请看，沿着哪条线能最快捉到苍蝇？为什么？（3）你发现了什么？生：两点之间线段最短。

（4）生活中的应用。

东村到水库要修一条管道，如果你是小小设计师，怎样设计最节约材料？请快速画出路线。

2.探究“距离”的概念。

（1）AB两点之间能再一条更短的线段吗？只能画这一条吗？师：两点之间这条唯一的线段的长度就是两点之间的距离。

（2）AB两点之间的距离是多少？生测量。

（3）找比AB这两点更远的距离。

①学生自己找。

②举例：黑龙江的抚远县和西藏的乌恰县，相距约4700千米。

地球和太阳的相距大约149600000千米。

师小结：长到几千米，短到几厘米，无论长短。

只要是：归纳：两点之间线段的长度，叫做两点之间的距离。

3.师总结这是我们这节课要学习的第一个知识点：两点间的距离。

【设计意图：通过蜘蛛吃苍蝇要走最短的路线，让学生非常形象的理解两点之间线段最短。

两点间的距离及点到直线间的距离教学内容：青岛版小学数学四年级上册60--61页。

教学目标：1.结合具体情境，感受并领悟“两点之间线段最短”、“点到直线的垂直线段最短”，知道两点之间的距离和点到直线的距离。

2. 在对知识的探究过程中，培养观察、想象、动手操作的能力，发展初步的空间观念。

3. 体验数学与日常生活的密切联系，提高学习兴趣，学会与他人合作共同解决问题。

教学重难点：教学重点：结合具体情境感受并理解“两点之间线段最短”、“点到直线的垂直线段最短”。

教学难点：“点到直线的距离”的理解与图形的画法。

教具、学具：多媒体课件、三角尺、直尺、彩笔、线团。

教学过程：一、创设情景，提出问题1、首先教师用多媒体出示信息窗2的情境，引导学生观察：2、学生随着教师出示的情境，边观察边交流发现的信息，在孩子观察了解信息的基础上诱导学生：根据这些信息你有什么疑问？预设学生的想法：⑴为什么要修隧道（挖山洞）？【部分农村孩子没见过隧道，会说成是山洞，教师简介这种建筑就是隧道。

】⑵能不能绕路过去？⑶从山上修一条盘山路。

……3、对于这些方法，同学们有什么意见？【孩子讨论、交流，初步体会到修隧道在交通中的重要性。

】今天这节课就请大家跟随老师一起研究修隧道中的数学知识。

【设计意图：通过现实生活中的情境，让孩子自主提出要解决的问题，体会生活中处处有数学，并逐步尝试从数学的角度分析问题。

】二、自主学习，小组探究。

1. 提出问题：刚才我们班同学认为修隧道的路程最近，其它的方法路程会远一些，这种观点对不对？我们应该怎样做才能证明我们的观点是否正确？2.制定研究计划。

给学生一个简易的大山图，在山的两侧分别标出两个点A和 B。

⑴从A 地到 B地，你能把修隧道的方法在图上表示出来吗？动手画一画。

你还能想到哪些不同的路线，试着画几条，看看能发现什么？⑵利用学具动手摆一摆、比一比、量一量，验证你的发现是否正确？⑶从中你能得出什么结论？并与小组同学交流。

点线面间的距离公式在几何学中，点、线、面是最基本的几何元素。

计算它们之间的距离是解决许多几何问题的关键步骤之一。

本文将介绍几种常见的点线面间距离公式，以帮助读者更好地理解和运用这些公式。

一、点到点的距离公式点到点的距离是最简单的情况。

假设有两个点A(x1, y1)和B(x2, y2)，它们之间的距离可以通过应用勾股定理来计算。

勾股定理的表达式如下：d = √((x2 - x1)² + (y2 - y1)²)其中，d表示两点之间的距离。

二、点到直线的距离公式点到直线的距离是指从给定点到直线上最近点的距离。

假设有一个点P(x0, y0)和一条直线Ax + By + C = 0，其中A、B、C是直线方程的系数。

点P到直线的距离可以通过下述公式计算：d = |Ax0 + By0 + C| / √(A² + B²)三、点到平面的距离公式点到平面的距离是指从给定点到平面上的最近点的距离。

假设有一个点P(x0, y0, z0)和一个平面Ax + By + Cz + D = 0，其中A、B、C、D是平面方程的系数。

点P到平面的距离可以通过下述公式计算：d = |Ax0 + By0 + Cz0 + D| / √(A² + B² + C²)四、线到线的距离公式线到线的距离是指两条直线之间的最短距离。

假设有两条直线L1和L2，可以通过求取两条直线间最短距离的垂直距离来计算线到线的距离。

五、线到平面的距离公式线到平面的距离是指线上的点到平面上的最近点的距离。

假设有一条直线L和一个平面Ax + By + Cz + D = 0，可以通过求取直线上一点到平面的垂直距离来计算线到平面的距离。

六、面到面的距离公式面到面的距离是指两个平面之间的最短距离。

假设有两个平面P1和P2，可以通过求取两个平面上的任意一点到另一个平面的垂直距离来计算面到面的距离。

结论点线面间的距离公式在几何学中起着重要的作用，它们可以帮助我们计算和解决各种几何问题。

高中数学辅导讲义[解析版]知识图谱点到直线的距离知识精讲一．点到直线的距离公式1. 两点的距离公式已知平面内两点()()1122,,,A x y B x y ，则两点距离()()222121AB d x x y y =-+-2.点到直线距离公式（1）公式：点()00x y ，到直线22:0(0)l Ax By C A B ++=+≠的距离：0022Ax By Cd A B++=+（2）公式的证明：如图，已知点()00P x y ，，直线22:0(0)l Ax By C A B ++=+≠.过点P 作PQ l ⊥于()11,Q x y ， 则PQ 即为点P 到直线l 的距离. 由距离公式，只要列出关于10x x -，10y y -的方程，就可求出这两点的距离. 证明过程如下：证明：设()11,Q x y ，PQ 所在直线方程l '：'0Bx Ay C -+=，将,P Q 代入l '可得： 0011'0'0Bx Ay C Bx Ay C -+=⎧⎨-+=⎩，两式相减得：0101()()0 B x x A y y ---=⋅⋅⋅⋅⋅⋅①. 将Q 点代入l ，得：110Ax By C ++=.()()101000110A x x B y y Ax By C Ax By C -+-+++=++=，l:Ax+By+C=0OQ x 1,y 1()P x 0,y 0()xy()()010100 A x x B y y Ax By C ∴-+-=++⋅⋅⋅⋅⋅⋅②①、②：()()010*******()()0B x x A y y A x x B y y Ax ByC ---=⎧⎪⎨-+-=++⎪⎩将①、②式平方相加：22222101000()[()()]()A B x x y y Ax By C +-+-=++，0022101022()()PQ Ax By Cd x x y y A B++∴=-+-=+二．平行直线间的距离1. 公式：两条平行线11:0l Ax By C ++=与22:0l Ax By C ++=之间的距离是：22d A B=+2. 证明：设一条垂直于12l l 、的直线与12l l 、分别交于P Q 、两点，()()1122,,,P x y Q x y .PQ 即为直线12l l 、间的距离.此时P Q 、两点满足，1110Ax By C ++=，0020Ax By C ++=，00122PQ Ax By C d A B++∴=+，002Ax By C +=-1222PQ d A B∴=+．三点剖析一．注意事项1．点到直线的距离点()00,P x y 到直线0Ax By C ++=的距离为0022Ax By Cd A B++=+．（1）如果给出的方程不是一般式，应先将方程化为一般式再进行求解． （2）若点P 在直线上，点P 到直线的距离为零，距离公式仍然成立. （3）点到几种特殊直线的距离：① 点()00,P x y 到x 轴的距离0d y =；② 点()00,P x y 到y 轴的距离0d x =； ③ 点()00,P x y 到直线x a =的距离0d x a =-； ④ 点()00,P x y 到直线y a =的距离0d y a =-. 2．两条平行直线间的距离两条平行直线11:0l Ax By C ++=与22:0l Ax By C ++=的距离为1222C C d A B-=+．使用公式时，两条直线均为一般式，且x y 、的系数分别相同，而不是对应成比例，因此当直线方程不满足此条件时，应先将方程变形．二．方法点拨点到直线的距离应用：在求角平分线方程、最值、证明问题的过程中通过解析几何法，构造点到直线的距离以及两点间的距离来求解.点到直线的距离例题1、 点到直线的距离为（）A. B. C. D.例题2、 过点()1,2A 且与原点相距为1的直线方程是_______例题3、 （2011北京高考文）已知点A （0，2），B （2，0）．若点C 在函数y=x 2的图象上，则使得△ABC 的面积为2的点C 的个数为（ ） A.4 B.3 C.2 D.1随练1、 求经过直线1:30l x y +-=和直线2:280l x y -+=的交点，且点()1,3P 到它的距离 为53的直线l 的方程．平行直线间的距离例题1、 到直线3410x y --=的距离为2的直线方程是（ ） A.34110x y --=B.34110x y --=或3490x y -+=C.3490x y -+=D.34110x y -+= 或 3490x y --=例题2、 两平行线分别过()3,0A 和()0,4B ，它们之间的距离d 满足的条件是（ ） A.03d <≤ B.04d << C.05d <≤ D.35d ≤≤随练1、 两条平行线4310x y +-=与8630x y ++=之间的距离是（ ） A.25 B.45 C.15 D.12点到直线的距离的应用例题1、 中，求平分线所在直线的方程． 例题2、 设，求证：拓展1、 点到直线的距离为2、 已知直线l 与直线1:6850l x y --=平行，且它们间的距离是3，求l 的方程．3、 经过点(3,5)M 的所有直线中距离原点最远的直线方程是什么．4、 （2011岳阳一中高一上期末文理）已知△ABC 中，A （1，1），B(m m ，C （4，2）其中（1＜m ＜4），求m 为何值时，△ABC 的面积最大；最大面积是多少？5、 已知过点且斜率为的直线与轴和轴分别交于点，过点分别作直线的垂线，垂足分别为，求四边形的面积的最小值．(1,2)P -86150x y -+=212172ABC ∆()()()3,32,27,1,A B C --、、A ∠AD ,a b R ∈222.22a b a b ++⎛⎫≥ ⎪⎝⎭(2,3)P -:1l x =()1,1A ()0m m ->l x y P Q 、P Q 、20x y +=,R S PRSQ答案解析点到直线的距离点到直线的距离例题1、 【答案】 B【解析】 由点到直线间的距离公式即可得． 例题2、【答案】 1x =或3450.x y -+=【解析】 （1）当过点()12A ，的直线与x 轴垂直时，则点()12A ，到原点的距离为1， 所以1x =为所求直线方程．（2）当过点()12A ，且与x 轴不垂直时，可设所求直线方程为()21,y k x -=- 即:20,kx y k --+=由题意有2211k k -+=+，解得3,4k =故所求的直线方程为()321,4y x -=-即3450.x y -+= 例题3、【答案】 A【解析】 设C （a ，a 2），由已知得直线AB 的方程为2x +2y=1，即：x+y -2=0点C 到直线AB 的距离为：d=22，有三角形ABC 的面积为2可得：S ABC =12|AB|d=12× 22×22=|a+a 2-2|=2得：a 2+a=0或a 2+a -4=0，显然方程共有四个根，可知函数y=x 2的图象上存在四个点（如上面图中四个点C 1，C 2，C 3，C 4）使得△ABC 的面积为2（即图中的三角形△ABC 1，△ABC 2，△ABC 3，△ABC 4）． 故应选：A 随练1、【答案】 直线为3140y -=或2401171460x y +-= 【解析】 解法一： 由30,280.x y x y +-=⎧⎨-+=⎩得直线1l 与2l 的交点坐标为514,33⎛⎫- ⎪⎝⎭．显然直线l 的斜率存在， 设所求直线l 的方程为14533y k x ⎛⎫-=+ ⎪⎝⎭，即335140.kx y k -++= 则()2231335145,393k k d k ⨯-⨯++==+-即2128085510,,39k k k k +=+==-将12,k k 代入得所求直线为3140y -=或2401171460x y +-=． 解法二：设所求直线方程为()()2830,x y x y λ-+++-=即()()()21830.x y λλλ++-+-= 点()1,3P 到l 的距离为53，()()()()222113835,321λλλλλ+⨯+-⨯+-=++-即241763160.2λλλ--=∴=-或15841λ=． 代入既得所求方程平行直线间的距离例题1、 【答案】 B【解析】 由题意可知两直线平行，故有1222222212,934C C C d C A B---===∴=++或211C =-，故直线方程为34110x y --=或3490x y -+= 例题2、 【答案】 C【解析】 两平行线重合时，距离最小0d =， 两点连线与平行线垂直时，距离最大22345d =+ 但两直线不能重合，故05d <≤ 随练1、 【答案】 D【解析】 由平行线间距离公式1222C C d A B -=+可知，223112243d --==+．点到直线的距离的应用例题1、【答案】【解析】 设为平分线上任意一点，由已知可求得边所在直线方程为，边所y x =(),M x y A ∠AD AC 5120x y -+=AB在直线方程为．由角平分线的定义，得或，即或，检验可知，不合题意．例题2、【答案】 见解析【解析】 证明：设为平面内任一点，则到直线的距离为点，即拓展1、【答案】【解析】2、【答案】 68350x y --=或68250x y -+= 【解析】 设直线l 的方程为225680,32568c x y cd c +-+===⇔=+或35c =-，故直线方程为68350x y --=或68250x y -+= 3、【答案】 35340x y +-=【解析】 过点(3,5)M 且垂直于OM 的直线为所求的直线，由直线OM 的斜率53k '= 则所求直线的斜率3,5k =-所求直线的方程为()3:535y x -=--； 化简得：35340x y +-= 4、【答案】 m=94，S max =18【解析】 本题考查点到直线距离公式的灵活运用，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．由22(41)(21)-+-10AC 的直线方程，利用点B 到直线AC 的距离是|32|10m m -+，S=12|AC|•d=12|m -m 12m 32)2-14|，由此能推导出当m=94时面积最大为S max =18．|AC|=22(41)(21)-+-10AC 的直线方程为x -3y+2=0，点B 到直线AC 的距离是|32|10m m -+，△S=12|AC|•d=12|m -m=12m 32)2-14| △1＜m ＜4，△1m 2，5120x y --=5125122626x y x y -+--=512512x y x y ∴-+=--512512x y x y -+=-++6y x =-+y x =6y x =-+(),M a b M y x =-2a b +M 22a b +22a b +2a b +222.22a b a b ++⎛⎫≥ ⎪⎝⎭121 1.d =-=△-1232＜12，32)2＜14，△S=12[14-32)2]，△32，即m=94时面积最大，最大面积为S max =18．5、【答案】【解析】 设直线的方程为，则，，从而可得直线和的方程分别为，，由∥，又四边形为直角梯形，又此时，，即四边形的面积最小值为3.6l ()11y m x -=--11,0P m ⎛⎫+ ⎪⎝⎭()0,1Q m +PR QS 120m x y m +--=()2210x y m -++=PRQS 132m RS ++∴==22PR QS +==PRSQ 22123211191.25480PRSQ m S m m ⎛⎫+++ ⎪⎛⎫∴==++- ⎪⎝⎭12,m m +≥1m =21912 3.65480S ⎛⎫∴≥+-= ⎪⎝⎭PRSQ 3.6。

两条直线的位置关系知识点及题型归纳
知识点精讲
一、两直线平行与垂直的判定
两条直线平行与垂直的判定以表格形式出现，如表9-1所示.
两直线方程
平行
垂直
(斜率存在)
(斜率不存在)
或
或 中有一个为0，另一个不存在.
二、三种距离
1．两点间的距离
平面上两点 的距离公式为 .
特别地，原点O(0,.0)与任一点P(x,y)的距离
简证：首先易知：若直线l关于直线 对称的直线是 ，则经过它们的交点（假定相交）且垂直于 的直线 也是l与 的同，故只证 的情形.
然后把每条直线都平移至过原点O，所得直线分别为 ，且
不妨在直线 上取异于O的点 ，则关于 对称的点为
故 ，所以 ，得证.
变式1 （1）求点P(4,5)关于点M(3,-2)对称的点Q的坐标；
2.已知两条直线y=ax-2和3x-(a+2)y+1=0互相平行，则a=( )
A.1或-3B.-1或3C.1或3D.-1或-3
3.直线y=3x绕原点逆时针旋转 ，再向右平移1个单位，所得直线（ ）
A. B. C. D.
4.设a,b,c分别是 中角A,B,C所对边的边长，则直线 与的 位置关系是（ ）
A. B.6C. D.
变式2 在等腰三角形ABC中，AB=AC=4，点P是边AB上异于A,B的一点，光线从点P出发，经BC,CA反射后又回到点P（如图9-9所示）.若光线QR经过 的重心，则AP等于（ ）
A.2B.1C. D.
有效训练题
1.若直线ax+2y+6=0和直线 垂直，则a的值为（ ）
A. B.0C. 或0D.-3
2．点到直线的距离
点 到直线 的距离