当前位置：文档之家 › 利用柱面坐标和球面坐标计算三重积分

利用柱面坐标和球面坐标计算三重积分

  • 格式：ppt
  • 大小：1.47 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

三重积分在柱面及球坐标系下的计算

三重积分在柱面及球坐标系下的计算

= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考： 思考：是否可考虑用切片法来求解？

例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习 试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法 直角坐标系(切片法)
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法 球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.

柱面坐标系和球面坐标系求三重积分

柱面坐标系和球面坐标系求三重积分

z x2 y2所围 .
分析 (V )为由半球面与锥面所围,
故可用球面坐标,
y
此 ,0 时 2 ,0 ,0R . x
4
2
I d
/4
d
R22sind
0
0
0
2 2 R5.
5
练习 试用三种坐标系算 分三 别重 计积分
I zdv,其中(V): x2 y2 z2 2z. (V)
解法1 直角坐标(切 系片法 )
x
则 (V )f(c o,s si,n z)d d dz ,
]d d
[ z2(,)f(co ,ssin,z)dz
( ) z1(,)
例1 计算三重积I分 (Vz)dv,
其中(V)由z R2 x2 y2与 z 0所围.
解 (V )向 xo 面 y 投 (x)y 为 影 :0 圆 R , 02 x
I d d
zdz
0
0 1 1 2
x
2012 12d
4 . 3
•1
xy
解法3 球面坐标系计算zdv (V) x2y2z22z
z
2
球面 : 为 2co,s其中
02 ,0,02co .s
2
o
y
I 2d /2d 2coscos2sxind
0
0
0
2/24co5ssind 4 .
0
3
z
h•
此,时 2zh.
I [ h 2dz ]dd ( xy ) 2
•
o•
x
y
( xy )
2d h(3h5)d
0
0
1 h3.
6
思考：本题是否也可考虑用切片法来求解？
4-2-2 球面坐标系下三重积分的计算

第三节三重积分计算法

第三节三重积分计算法

设M（x,y,z）为空间
z
一点，如果将x，y，z
改用另外三个数r，,z
来表示，则称（r, ,z） O r
为点M的柱面坐标。
x
M (x, y, z)
z
y
P(r, )
在xoy面上 r, 就是极坐标
由图可知柱面与直角坐标的关系是
x r cos
y
r
sin
(0 r ,0 2 , z )
且被积函数含有
x2 y2, y x
常用极柱坐标
2.球面坐标
由球面坐标与直角坐标的关系：
x r sin cos 0 r
y
r
sin
sin
z r cos
,
0
0 2
体积元素
三重积分在球面坐标系下的形式：
f (x, y, z)dv F(r,,)r2 sindrdd
其中 F(r,,) f (r sin cos, r sin cos, r cos)
4
所以 zdxdydz rdrd r2 zdz
D
2
2
4
d rdr zdz
0
0
r2
1
2
d
2 r(16 r2 )dr
20
0
1 2
2 [8r 2
r2 6
]02
64 3
例6 计算 I (x2 y2)dv 其中
由锥面x2 y2 z2 , x 0, y 0
和z a a 0所围成第一卦限 z z a
f (x, y, z)dv
球面方程：r a
2
d
d
a F(r,, )r2 sindr
0
0
0
一般地，空间区域 包含原点在其内

2.5利用柱面坐标和球面坐标计算三重积分

2.5利用柱面坐标和球面坐标计算三重积分
规定: 规定: 0 ≤ r < +∞ ,
0 ≤ θ ≤ 2 π,
z
M ( x,
∞ < z < +∞ .
o
θ
y, z )
r
P (r ,θ )
y
x
如图, 如图,三坐标面分别为
r 为常数
圆柱面; 圆柱面; 半平面; 半平面; 平 面.
z
θ 为常数
z 为常数
M ( x, y , z )
z
柱面坐标与直角坐 标的关系为 x = r cosθ , y = r sinθ , z = z.
o
θ
r
P (r ,θ )
y
x
讨论下列柱坐标系下的曲面方程表示的曲面
Answer : (a ) r = 5 x 2 + y 2 = 55
(b) (c )
Question: In rectangular coordinates the volume element dV is given by dV=dxdydz, dV=dxdydz,
D1 2
8
2π
0
45 dθ ∫ dr ∫r 2 r r 2dz = π , 0 3 2
4 8
I 2 = ∫∫ rdrdθ ∫r 2 fdz = ∫
D2 2
2
2π
0
25 dθ ∫ dr ∫r 2 r r 2dz = π , 0 2 6
2 2
45 25 原式 I = π π = 336π . 3 6
球面坐标与直角坐标的关系为
x = ρ sin cosθ, y = ρ sin sin θ, z = ρ cos.
A
x
ρ M ( x , y, z )

柱坐标、球坐标下的三重积分

柱坐标、球坐标下的三重积分

解：由图知：直角系：
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系： I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分，
z
其中：z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标：(θ,r,z)
zz
变换为：x r cos , y r sin , z z
即：(x, y, z) (r cos , r sin , z),其中：
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注：柱坐标— 极坐标平面竖起一根Z轴。x
上顶： z 1 x2 y2
下底： z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标？ 柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注：用柱坐标求 fdv分成两个步骤：
第一步：先一后二，对z积分后将二重积分化为极坐 标下的二重积分；
元素区域由六个坐标面围成：
半平面及+d ;
半径为r及 r+dr的园柱面；
平面 z及 z+dz；
dz

柱面坐标和球面坐标计算定积分

柱面坐标和球面坐标计算定积分
一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2

利用柱面坐标和球面坐标计算三重积分

利用柱面坐标和球面坐标计算三重积分

2
D2 : x2 y 2 4, 2 :
D1 D2
0 2
0 r 2
r
2
z
. 2
2
I I1 I2
( x2 y2 )dxdydz ( x2 y2 )dxdydz,
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
3.5 利用柱面坐标和球面坐标 计算三重积分
一、利用柱面坐标计算三重积分 二、利用球面坐标计算三重积分
三、小结
一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
圆柱面；
z
为常数
z 为常数
半平面； 平 面．
• M (x, y, z)
z
柱面坐标与直角坐 标的关系为
or
• P(r, )
y
x r cos ,
y
r
sin
,
x
z z.
如图，柱面坐标系 中的体积元素为
x2 y2 z2， 与平面z a (a 0) 所围的立体.
解: 采用球面坐标
za r a , cos
x2 y2 z2 ,
4
: 0 r a , 0 , 0 2,

利用柱面坐标计算三重积分

利用柱面坐标计算三重积分
`z
z
j r
zdv

dvΒιβλιοθήκη zdvO
dv

a 2 0 2
．
q
x
a y
dv 2 dj dq


2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分

，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲

面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz

2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2

3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z

谈谈三重积分的定限方法

谈谈三重积分的定限方法

谈谈三重积分的定限方法计算三重积分的基本方法是将三重积分化为三次积分来计算，而这里的一个关键问题是如何根据积分区域Ω来定限，下面分别介绍一下利用直角坐标，柱面坐标，球面坐标计算三重积分时如何定限的方法。

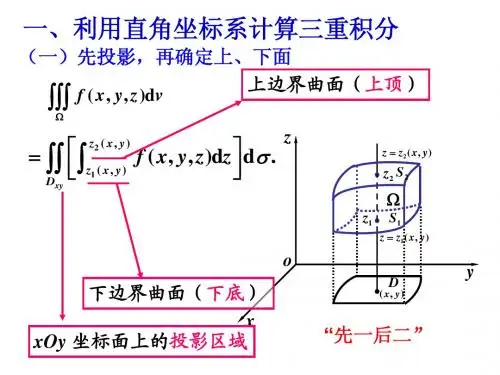
一、利用直角坐标计算三重积分时如何定限？ 教材中将积分区域Ω表示为:}),()(:),(),,(),(),,{(2121b x a x y x y x y x z y x z y x yy D zz xy ≤≤≤≤∈≤≤=Ω(1)从而将三重积分化为三次积分为：⎰⎰⎰⎰⎰⎰Ω=D z z dz z y x f dxdy dv z y x f xyy x y x ),(),(21),,(),,(=dz y y z z z y x f dy dx x x y x y x ba ⎰⎰⎰)()(),(),(2121),,(这个公式也称为“先一后二”积分公式。

（上述公式是将Ω向xoy 平面投影得到的，将Ω向其他坐标平面投影可得到类似的公式）当积分区域的几何形体较简单时，容易写出Ω的集合表达式（1），但积分的区域的立方图形通常难以画出,因此确定Ω的集合表达式（1）较困难。

为了解决这个困难。

下面介绍一个所谓“求围定顶”的定限法：称（1）式中),(1y x z ，),(2y x z 分别为区域Ω的下顶和上顶，以D xy 的边界曲线为准线，母线平行于Z 轴的柱面，位于下顶和上顶之间的部分称为Ω的“围墙”，Dxy的边界曲线称为“围线”，（它是投影柱面与xoy 平面的交线），下面分三种情况来介绍“求围定顶”的定限法。

1.设Ω由曲面),(y x h z =与),(y x g z =围成，不出现“围墙”，此时两曲面的交线在xoy 平面上的投影即为“围线”。

例 1.化三重积分⎰⎰⎰Ωυd z y x f ),,(为三次积分，其中Ω为由曲面2222,2x z y x z -=+=围成的闭区域例：“求围” 由方程组{22222xz y x z -=+=消去z 得两曲面交线在xoy 平面上的投影，即“围线”：122=+y x ，因此1:22≤+y x D xy ，即 .11,11:22≤≤--≤≤--x x y x D xy“定顶” 在Dxy内任取一点代入两曲面方程),(y x h z =，),(y x g z =得到两个z 的值，大者为上顶，小者为下顶。

利用柱面坐标和球面坐标

利用柱面坐标和球面坐标

o

y
为常数 半平
面．
x
球面坐标与直角坐标的关系为
x r sin cos ,

y

r
sin

sin
,
z r cos .
z
r M(x,y,z)
z
o
x
A

y
x

P
y
如图， 球面坐标系中的体积元素为
d vr2sin dd r d,
z
dr
d
rsin
r

rsin d
例3 计算三重积分 (x2y2)dv, 其中 是由曲

面 z x2y2与平 zH 面 (H0)所围成
z
解 将 向 xoy 面投影，得
D: x2y2H2
HH
或
D:
0 2,
0rH.
过 (r, )∈D 做平行于 z 轴
的直线，得
rzH .
o(r,)
r sin cos , r sin sin , r cos.
02d0 co2ssinr551 0d d vr2sin drd d
1 50 2 d0 co 2sin d
1 50 2d0 co 2s d(co ) s
例4 用球面坐标计算 z2dv . 其中
z

: x2y2z21.
解 画 图。
o
y
确定 r， ， 的上下限。 x
(1) 将 向 xoy 面投影，得
0 2 .
(2) 任取一 [0,2],过 z 轴作半平面，得
0.
(3) 在半平面上，任取一 [0,], 过原点作
rd
d

三重积分计算方法

三重积分计算方法

(1 y z )2
Dyz
1 dy
0
1
x
1 1 y -(1-y )2 (1 e )dy 0 4e 2
1
y
0
(1 y )(1 y z )e
-(1-y-z )2
例4 计算 ( z 2 x )dv， : x 2 y 2 z 2 R 与
于是引力F在三个坐标方向上的分量为
m ( x , y , z )( x a ) Fx G dv, 3 r V m ( x , y , z )( y b) Fy G dv, 3 r V m ( x , y , z )( z c ) Fz G dv. 3 r V

,
M zx y M
y ( x , y, z )dV ( x , y, z )dV

x
, z M xy M
o x


z
dV y
y
z ( x , y, z )dV ( x , y, z )dV

(二) 转动惯量
(1) 平面薄片的转动惯量
y
y
I x y 2 ( x , y )d
x 2 y 2 2az 所围成立体的表面积. z
a
o
x
y
例10 求半球面 z 3a 2 x 2 y 2与旋转抛物面
x 2 y 2 2az 所围成立体的表面积. z
S = S1 S2
S1
S2
. .
o
D
.
2a
y
z 3a 2 x 2 y 2 D: 2 2 x y 2az x 2 y 2 2a 2 即 z 0

第三节 三重积分(2).

第三节 三重积分(2).

在D内任取一点( , )
作与z轴平行的直线
Dxy
0
2y
从曲面z x2 y2穿入内，
从平面z 4穿出外
x
机动 目录 上页 下页 返回 结束
0 2
则 : 0 2
故
2 z 4
zdxdydz zdddz
2
2
4
d d zdz
0
0
2
1
2
d
2 (16 4 )d
20
dz
2
1 0
( 1 1
2
1)d
(ln 2
2
.
) 2
.
.
.
Dxy
x
1
0
1y
机动 目录 上页 下页 返回 结束
【例2】利用柱面坐标计算三重积分 zdxdydz
其中是由曲面z x2 y2与平面z 4所围闭域
z
【解】将投影到xoy面得D :
D : x2 y2 4
4
即
D : 0 2 ,0 2
以下举例说明
机动 目录 上页 下页 返回 结束
【例1】I
Ω
1 dxdydz
x2 y2 1
:锥面 x y z ,
【解】 用柱面坐标 锥面化为: ρ= z
z
上顶：z = 1 下底： z
z 所围
Dxy: 0 2 ,0 1
I
D
dd
1
1 2
dz 1
2
d
0
1 0
2
1
d
1
0
[8
2
1 6
6 ]02
64
3
【思考】 本题是否可考虑用截面法来求解？

齐民友高数下册上课第10章05柱面坐标与求面坐标系中三重积分的计算(1)

齐民友高数下册上课第10章05柱面坐标与求面坐标系中三重积分的计算(1)

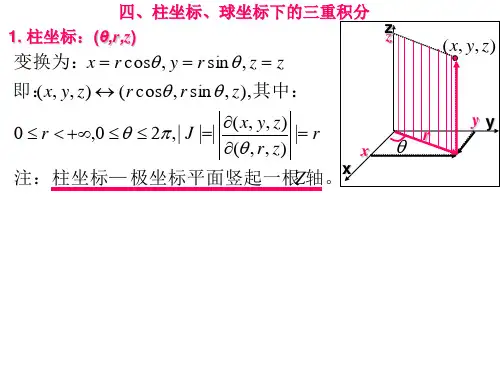
第5节 柱面坐标与球面坐标系下三重积分的计算5.1 利用柱面坐标计算三重积分我们不按课本上的讲法，换一种讲法。

用柱面坐标计算三重积分的步骤： （1）把三重积分写成二套一：将往xOy 平面投影得xy D，设的小z 边界1(,)zz x y 大z 边界2(,)zz x y ，则21(,)(,)(,,)d (,,)xyz x y z x y D f x y z vdxdyf xy z dz（2）用极坐标计算外层的二重积分： 设12(,)|()(),xyD则212211(,)(,)()(cos ,sin )()(cos ,sin )(,,)d (,,) (cos ,sin ,)xyz x y z x y D z z f x y z vdxdyf x y z dzd df zdz注意：用极坐标计算外层二重积分时，总是先对后对积分；用坐标关系cos x ，sin y 代入被积函数和里层定积分的上下限，z不动，并且外层面积元素多一个因子，即dxdyd d ，或说体积元素dxdydzd d dz ．当然，当投影区域xy D 的边界有圆弧或被积函数有22x y 时用柱面坐标计算简单。

离 散数 学【例5.1】 计算三重积分22()d xy v ，其中是由曲线220y z x绕z轴旋转一周而成的曲面与平面2z所围成的区域．解 旋转面的方程为：222x yz ．如图5.1所示，将积分区域投影到xOy 面，得投影区域为：22(,)|4xyD x y x y ．的小z 边界222x y z 大z 边界2z 。

积分区域为：222212(,,)|()2,4x y z x y zx y ，所以2222222222222100222220246()d () 1 d(2)d 211162()2123xy x y D xy vdxdy x y dz d ddz图5.1我们看到，上面计算方法中，用,,z 作坐标（变量）。

设空间有一点(,,)M x y z ．并设M 在xOy 面上的投影点P 的极坐标为,，则这样三个数,,z 就叫做点M 的柱面坐标．一般地,,z 的取值范围为： 0，02，z ．容易看出，所谓柱面坐标，就是：z 不变还是z ，而,x y 换成极坐标。

7.4.2 三重积分的计算(柱面、球面)

7.4.2 三重积分的计算(柱面、球面)

上一页 | 首页 | 下一页
College of mathematics March 27, 2012
参数方程： 参数方程：
x = s cos ω t y = s sin ω t z = vt
y v z = arctan = θ ω x ω
上一页 | 首页 | 下一页
College of mathematics March 27, 2012
v
是圆域时， 当 Ω 在 xOy 面上的投影区域 D 是圆域时， 用柱面坐标计算三重积分比较方便
在“先一后二”的二重积分中需要用极坐标 先一后二” 积分时， 积分时，我们实际上就在使用柱面坐标计算 三重积分
上一页 | 首页 | 下一页
College of mathematics March 27, 2012
例4.4
∫∫∫ ( x + y )dV
2 2 Ω
Ω: x + y ≤ z ≤ 2
2 2
Ω
是一个圆锥体
z=2
z = x2 + y 2
它的投影区域是一个圆域 宜用柱面坐标计算
z = x + y z = 2
2
2
D
D:x + y ≤ 4
2 2
上一页 | 首页 | 下一页
College of mathematics March 27, 2012
dσ
March 27, 2012
with(plots):x_axis:=plot3d([u,0,0],u=0..3,v=0..0.01,thickness=2): y_axis:=plot3d([0,u,0],u=0..3,v=0..0.01,thickness=2):

高数讲义第三节三重积分(二)

高数讲义第三节三重积分(二)

Dxy : 0 2 , 0 a
x2 y2 z2 z ,
4
o
y
: 0 2 , 0 a, z a, x
Dxy
I ( x2 y2 )dxdydz 02 d 0ad a 2dz
2 0a 3(a )d
a5. 10
解 由锥面和球面围成， 采用球面坐标，
: 0 2 , 0 2, 2 z 4，
例 5 计算 I zdxdydz，其中 是抛物面
z x2 y2及平面 z = 4 所围的立体. z
解
Dxy {(x, y) | x2 y2 4}
{(, ) | 0 2 , 0 1}
z1 x2 y2 2, z2 4,
3
z2 2
4 2
d
2
3
二、利用球面坐标计算三重积分
球面坐标：设 M ( x, y, z) 为空间内一点， 点 M 到原点的距离记为 r ,
有向线段 OM 与 z 轴正向的夹角记为 ，
点 M 在xoy 面上的投影 为P ( x, y)
自x 轴按逆时针方向旋转到有向线段 z
OP 的角度记为
则三元有序数组( r, , )
例 5 计算I zdxdydz，其中 是抛物面.
z x2 y2及平面 z = 4 所围的立体. z
解
由
z
x2
y2 ,
z 4
知曲面与平面的交线为
x2
y2
4,
z4
o
y
x
Dxy {(x, y) | x2 y2 4} {(, ) | 0 2 , 0 2}
z1 x2 y2 2, z2 4,
y
sin
,
z z.
o
• P(, )

9.5_三重积分计算2

9.5_三重积分计算2

一般地，先对 ，后对r， 一般地，先对z，后对 ，最后对 θ 积分
二、利用球面坐标计算三重积分
z
设 M ( x, y, z ) 为空间内一点， 则点 M 可用三个有次序的数r，
A
x
r
M ( x,
z
y, z )
o
P ，θ 来确定，其中 r 为原点 O 与 x 点 M 间的距离， 为有向线段 OM 与 z轴正向所夹的 角，θ 为从正 z 轴往下看自 x 轴按逆时针方向转到有
0
π 2 0
π 2 0
R
x
.
例 4、 求曲面 x2 + y2 + z2 ≤ 2a2与 z ≥ x2 + y2 成的立体体积. 所围 成的立体体积
解
由x
2
由锥面和球面围成， 采用球面坐标， 由锥面和球面围成， 采用球面坐标，
+ y + z = 2a
2 2
2 2
2
r = 2a ,
z=
π x + y = , 4
z
M ( x,
∞ < z < +∞ .
x = r cos θ , 直角坐标与柱面坐标的关系为 y = r sin θ , z = z.
o
θ
y, z )
r
P (r ,θ )
y
x
柱面坐标的坐标面 动点M( 动点 r, θ, z) z r =常数：圆柱面 常数： 常数 圆柱面S z =常数： 平面Π 常数： 常数 S
‘
= abc ∫ dθ ∫ sin d ∫ 1 r 2 dr =
0 0 0
2π
π
1
π2
4
例7、计算∫∫∫ ( x + y + z ) cos( x + y + z ) 2 dxdydz

极坐标与球面坐标计算三重积分

极坐标与球面坐标计算三重积分
4 3
3 a
2π
π
4 其中 M = πa 3 ρ 为球体的质量． 3
0
2πa 3 , r 2 sin ϕdr = 3
a
1 a4 zdv = ∫ 2 dϕ ∫ dθ ∫ r cos ϕ ⋅ r 2 sin ϕdr = ⋅ 2π ⋅ , ∫∫∫ 0 0 0 2 4 Ω 3a 3a 因此z= ．重心为(0，0， )． 8 8
2π
π
例4 求均匀球体对于过球心的一条轴l 的转动惯量． 解 取球心为坐标原点，z轴与轴l重合，又设球的半径为a， z 则球体所占空间闭区域Ω可用不等式 x2+y2+z2≤a 2 来表示． 所求转动惯量为
θ =θ 0
y
θ0
直角坐标与柱面坐标的关系：
z z M(x, y, z)
x = r cos θ , y = r sin θ , z = z.
柱面坐标系中的体积元素： dv =rdrdθdz． 柱面坐标系中的三重积分： x
Ω
O x
θ
r
y P(r, θ )
y
∫∫∫ f (x，y，z)dxdydz = ∫∫∫ f (r cos θ
V= ∫∫∫ dxdydz = ∫∫∫ r2 sinϕ drdϕdθ
Ω Ω
= ∫ dθ ∫ dϕ ∫
0 0
2π
α
2 a cos ϕ
0
r 2 sin ϕdr
= 2π ∫ sin ϕdϕ ∫
0
α
2 a cos ϕ
ϕ r α O x y
0
r 2 dr
16πa 3 α = cos 3 ϕ sin ϕdϕ 3 ∫0 4πa 3 = (1 − cos 4 a) ． 3

利用柱面坐标与球面坐标计算三重积分

利用柱面坐标与球面坐标计算三重积分

f ( r cos , r sin , z )rdrddz.

rdrd
Dr
z2 ( r , ) z1 ( r , )
f ( r cos , r sin , z )dz .
通常化为先对 z、再对 r、后对θ 的三次积分.
先将Ω在xOy面上的投影域用极坐标不等式表示
设M(x, y, z)为空间内一点,记向量OM来自长为r , OM与z轴z

r
M ( x, y, z )
z
正方向间的夹角为 , 再将OM
A x
x
O

y

y
P
向xOy平面投影, 记投影向量与x轴正方向的 夹角为 , 称 ( r , , ) 为点M的球面坐标. 规定 0 r , 0 , 0 2 .
=常数: 半平面P
0

y
x
直角坐标与柱面坐标的关系为
x r cos , y r sin , z z.
在柱面坐标下 1. 若被积函数形如
x y r . 因此
2 2 2
f (x y ) ;
2 2
2. 积分区域Ω是由柱面、锥面、旋转抛物面、平 面或球面所围成.
y
球面坐标下的体积元素
z
元素区域由六个坐标面围成：
圆锥面
球面r+d r
半平面 及+d ； 圆锥面及+d
rsind
半径为r及r+dr的球面；
r
圆锥面+d
1
1
2 1dr 2 0 1 r
1
1 r
Dxy
0
1
y

三重积分计算中柱面坐标与球面坐标“定限问题”研究

三重积分计算中柱面坐标与球面坐标“定限问题”研究

三重积分计算中柱面坐标与球面坐标“定限问题”研究发表时间：2019-06-13T15:06:15.627Z 来源：《知识-力量》2019年9月30期作者：吴文前[导读] 计算三重积分时积分上下限的确定非常重要。

关乎后面运算的正确或错误。

本文通过对三重积分计算中柱面坐标与球面坐标“定限”方式的差异研究，明确二者在穿越法定限应用时的不同点，帮助学生掌握定限方法，正确确定积分的上下限，明晰解题思路，减少计算错误。

（成都大学信息科学与工程学院，610021）摘要：计算三重积分时积分上下限的确定非常重要。

关乎后面运算的正确或错误。

本文通过对三重积分计算中柱面坐标与球面坐标“定限”方式的差异研究，明确二者在穿越法定限应用时的不同点，帮助学生掌握定限方法，正确确定积分的上下限，明晰解题思路，减少计算错误。

关键词：高等数学；三重积分；柱面坐标；球面坐标我们知道关于计算三重积分的计算一般都要化成三次积分来计算，于是关于积分上下限的确定就显得尤为重要。

如果上下限确定错误，必将导致后面运算的错误。

因此关注三重积分计算中柱面坐标与球面坐标“定限”方式的差异，通过例题分析示范，让学生明确二者的不同之处。

下面从三个方面谈谈：三重积分选择坐标系求解的注意事项。

通过举例，帮助学生掌握定限方法，正确确定积分的上下限，明晰解题思路，减少计算错误。

一、选择合适的坐标系是计算三重积分的关键：方法二：采用柱面坐标计算综上，我们看到：1、有些题目有多种方法可以选择，选择哪一类计算的方法，需要根据积分区域以及被积函数的特征来对比决定方法的利弊。

2、不管利用哪一种坐标系来计算“三重积分”，一定要正确使用好“穿越法”来确定上下限。

在实际教学过程中，我们可以通过更多的实例让学生探索：如何通过适当选择坐标系来求解“三重积分”以达到简化运算的目的。

这样，不仅让学生体验到学数学的乐趣，也同时学会了如何对知识进行归纳总结，更让他们能够最终达到知识的融会贯通。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dv rdrddz,
z
rd
dr
r
dz
o
f ( x, y, z)dxdydz
y
d
x
f (r cos ,r sin , z)rdrddz.
例1 计算I zdxdydz，其中 是球面
x2 y2 z2 4与抛物面 x2 y2 3z
所围的立体.
x r cos
解
由
y
r
sin
,
z z
x2 y2 z2， 与平面z a (a 0) 所围的立体.
解: 采用球面坐标
za r a , cos
x2 y2 z2 ,
4
: 0 r a , 0 , 0 2,
cos
4
I ( x2 y2 )dxdydz
2
d
4 d
a
cos r 4 sin 3dr
0
球 面； 圆锥面； 半平面．
如图，
z
设点 M 在 xoy 面上的投影为P，
r
• M(x, y,z)
点 P 在 x 轴上的投影为 A，
z
则 OA x, AP y, PM z.
o
x
A
xy
•
P
y
球面坐标与直角坐标的关系为
x r sin cos ,
y
r
sin
sin
,
z r cos .
如图，
I2 rdrd r2 fdz
D2
2
2
2
d dr
0
0
2
r2 2
r
r 2dz
25 6
,
原式I 45 25 336 . 36
二、利用球面坐标计算三重积分
设 M (x, y, z) 为空间内一点，则点
M 可用三个有次序的数r，， 来确 z
定，其中r 为原点O 与点 M 间的距离，
r • M(x, y,z)
是曲线 y2 2z ，x 0 绕oz 轴旋转一周而成
的曲面与两平面z 2,z 8 所围的立体.
解
ห้องสมุดไป่ตู้
由
y
2
2z
绕 oz
轴旋转得，
x0
旋转面方程为 x2 y2 2z,
所围成的立体如图，
所围成立体的投影区域如图，
D1 : x2 y2 16,
0 2
0 r 4
1 :
r
2
z
, 8
0
0
r2
(90 2 89). 60
补充：利用对称性化简三重积分计算
使用对称性时应注意： １、积分区域关于坐标面的对称性；
２、被积函数在积分区域上的关于三个坐标轴 的 奇偶性．
一般地，当积分区域关于 xoy平面对称，且 被积函数 f ( x, y, z)是关于z的奇函数，则三重积分 为零，若被积函数 f ( x, y, z)是关于z的偶函数，则 三重积分为在 xoy平面上方的半个闭区域的三重 积分的两倍.
为有向线段OM与 z轴正向所夹的角， o
z
为从正 z 轴来看自x 轴按逆时针方向
转到有向线段OP 的角，这里 P 为点 M
x
A
xy
•
P
y
在 xoy 面上的投影，这样的三个数 r，，
就叫做点M 的球面坐标．
规定： 0 r , 0 , 0 2.
如图，三坐标面分别为
r 为常数
为常数 为常数
例 6 利用对称性简化计算
z
ln( x2 x2
y
y2 2
z2 z2
1
1)
dxdydz
其中积分区域 {(x, y, z) | x2 y2 z2 1}.
解 积分域关于三个坐标面都对称，
被积函数是 z 的奇函数,
z
球面坐标系中的体积元素为 d
dr
r sin
r sind
dv r2 sindrdd ,
r
rd
d
o
y
f ( x, y, z)dxdydz
d
x
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
0
0
2
4 0
sin
3
1 5
(
a5 cos5
0)d
a5. 10
例 4 求曲面 x2 y2 z2 2a2与z x2 y2 所围 成的立体体积.
解 由锥面和球面围成， 采用球面坐标，
由 x 2 y2 z 2 2a 2
r 2a,
z x2 y2 ,
4 : 0 r 2a, 0 ,
解法（一）
在球面坐标下分成两个部分：
V1
:
0
2
,0
4
,0
r
2;
V2
:0
2 ,
4
2
,0
r
cos sin2
;
解法（二）(类似于例1) 在柱面坐标下：
0 2, 0 r 1, r2 z 2 r2 ,
投影区域 Dxy ：x2 y2 1,
2
1
I d rdr
2r2 z2 2r(cos sin )z r2 (1 sin 2 ) dz
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
圆柱面；
z
为常数
z 为常数
半平面； 平 面．
• M (x, y, z)
z
柱面坐标与直角坐 标的关系为
or
• P(r, )
y
x r cos ,
y
r
sin
,
x
z z.
如图，柱面坐标系 中的体积元素为
3.5 利用柱面坐标和球面坐标 计算三重积分
一、利用柱面坐标计算三重积分
二、利用球面坐标计算三重积分
三、小结
一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
4
0 2,
由三重积分的性质知 V dxdydz,
V
2
d
4 d
2a r 2 sin dr
0
0
0
2
4
sin
(
2a )3 d
4 (
2 1)a3 .
0
3
3
例 5 计算 ( x y z)2dxdydz其中是由抛物
面 z x2 y2和球面 x2 y2 z2 2所围成的空 间闭区域.
知交线为
r2 z2 4
r2 3z
z 1, r 3,
把闭区域 投影到 xoy 面上，如图，
: r2 z 4 r2， 3 0 r 3, 0 2.
I
2
3
4r2
0
d 0
dr r2
3
r zdz
13 . 4
例２ 计算 I ( x2 y2 )dxdydz， 其中
2
D2 : x2 y 2 4, 2 :
D1 D2
0 2
0 r 2
r
2
z
. 2
2
I I1 I2
( x2 y2 )dxdydz ( x2 y2 )dxdydz,
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2