三重积分在柱面及球坐标系下的计算

格式：ppt
大小：782.50 KB
文档页数：14

下载文档原格式

/ 14

柱面坐标系求三重积分公式

柱面坐标系求三重积分公式在数学和物理学中，三重积分是一种用于计算立体空间内某个数量的数学方法。

在柱面坐标系中求三重积分是一种常见且有效的方法，它可以帮助我们解决与立体空间相关的问题。

在本文中，我们将探讨柱面坐标系下如何计算三重积分，并推导出相应的公式。

首先，我们回顾一下柱面坐标系的定义。

在柱面坐标系中，一个点的位置由三个坐标确定：径向距离r、极角$\\theta$以及高度z。

与直角坐标系不同，柱面坐标系提供了一种更方便描述圆柱面内点的方式。

要计算柱面坐标系下的三重积分，我们需要了解如何表示微元体积和如何变换积分元素。

微元体积在柱面坐标系下的表示可以通过微元体积元素dV来描述。

在柱面坐标系中，微元体积dV可以表示为：$dV = r dz dr d\\theta$。

这个表示方式是基于极坐标系的性质推导出来的，通过将微小的径向、高度和角度方向上的长度相乘得到微元体积。

接下来，我们来推导柱面坐标系下的三重积分公式。

假设我们要计算函数$f(r, \\theta, z)$在柱面坐标系下的三重积分，积分区域为D。

那么，三重积分的表达式可以写成：$$\\iiint\\limits_D f(r, \\theta, z) dV = \\int\\limits_{\\alpha}^{\\beta}\\int\\limits_{h_1(r, \\theta)}^{h_2(r, \\theta)} \\int\\limits_{g_1(r)}^{g_2(r)} f(r, \\theta, z) r dz dr d\\theta$$在上式中，$\\alpha$和$\\beta$表示极角$\\theta$的取值范围，$h_1(r,\\theta)$和$h_2(r, \\theta)$表示高度z的取值范围，g1(r)和g2(r)表示径向距离r的取值范围。

通过这个公式，我们可以将柱面坐标系下的三重积分问题转化为累次积分的计算问题，便于我们进行计算。

柱面坐标求三重积分

柱面坐标求三重积分引言积分在数学和科学中起着非常重要的作用，它可以帮助我们求解曲线、曲面和体积等问题。

在三维空间中，我们经常遇到需要求解三重积分的情况。

本文将介绍柱面坐标系下求解三重积分的方法和步骤。

什么是柱面坐标系柱面坐标系是一种常用的三维坐标系，它使用极径r、极角θ和z轴坐标z来描述空间中的点。

在柱面坐标系中，一个点的坐标可以表示为(r,θ,z)，其中r表示点到z轴的距离，θ表示点在x-y平面上的极角，z表示点在z轴上的高度。

柱面坐标系下的坐标变换在求解柱面坐标系下的三重积分之前，我们需要了解柱面坐标系和直角坐标系之间的坐标变换关系。

根据几何关系可以得到以下变换公式：•x=rcos(θ)•y=rsin(θ)•z=z这些公式可以帮助我们将直角坐标系下的积分问题转换为柱面坐标系下的积分问题。

柱面坐标系下的积分元素在柱面坐标系下，积分元素可以表示为dV=r dr dθ dz，其中r表示点到z轴的距离，dr表示r的微小变化量，θ表示点在平面上的极角，dθ表示θ的微小变化量，dz表示z轴坐标的微小变化量。

柱面坐标系下的三重积分使用柱面坐标系求解三重积分的步骤如下：1.确定积分区域：首先需要确定积分区域，可以通过图形来确定。

在柱面坐标系下，积分区域可以使用极坐标和直角坐标的关系来表示。

2.写出被积函数：根据问题的具体要求，将被积函数用柱面坐标系下的变量表示。

3.确定积分限：根据积分区域的几何性质，确定积分区域的上下限。

4.变量代换：根据柱面坐标系和直角坐标系之间的坐标变换关系，将被积函数和积分元素用柱面坐标表示。

5.进行积分计算：根据确定的积分限和变量代换，进行积分计算。

柱面坐标系下的应用举例例子1：求解柱面体的体积柱面体是由一个半径为R的圆在z轴上从z=a到z=b旋转一周形成的立体。

我们希望求解柱面体的体积。

1.积分区域：由于柱面体是由圆旋转形成的，因此积分区域可以用圆的极坐标来表示：0≤r≤R,0≤θ≤2π,a≤z≤b。

微积分：利用柱坐标计算三重积分

a Dxy
r
,
cos
x
o
y
z x2 y2
I
4
a
2 4 cos
d d r 2 sin2 r 2 sin dr
x r sin cos
y
r
sin
sin
z r cos
00 0
dv r2 sin drdd
I ( x2 y2 )dxdydz
2
a
d 4 d cos r 2 sin2 r 2 sin dr
2
2
dz d
ze z2 rdr
1
0 0r
2 2 ez2 zdz (e4 e). 1
z
z2
z x2 y2
z1
O
y
x
y Dz
x
x2 y2 z2
计算(x y z)2dv,
其中是抛物面 z
x2
y2和球面x2
y2
z
z2
2
所围成的空间闭区域.
解 ( x y z)2 x2 y2 z2 2( xy yz zx)
且当( x, y) Dxy时, x2 y2 z 2 x2 y2 ,
Dxy : x2 y2 1,
y Dxy
x
x2 y2 z 2 x2 y2,
x2 y2 1
2 x2 y2
V 1 dv dxdy
1 dz
x2 y2
Dxy
(2 2 x 2 2 y 2 )dxdy
Dxy
2
2
d
1 (1 r 2 )rdr
0
0
0
0
t (0, )
0 r t
所以,F (t)在(0, )内单调增加.

三重积分的各种计算方法

三重积分的各种计算方法三重积分是微积分中的一种重要工具，用于计算三维空间中的体积、质量、质心等问题。

在实际应用中，我们经常需要计算三维物体的体积、密度、质心位置等信息，而三重积分提供了一种有效的方法来解决这些问题。

在本文中，我们将介绍三重积分的各种计算方法，包括直角坐标系下的直接计算方法、柱坐标系和球坐标系下的变量变换方法等。

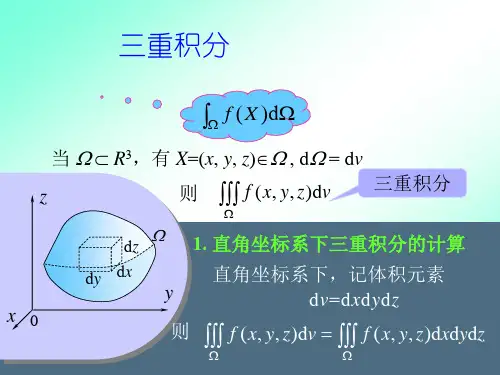
一、直角坐标系下的直接计算方法直角坐标系是我们最常见的坐标系，三重积分在直角坐标系下的计算方法较为直观。

我们以计算三维实体体积为例来介绍直角坐标系下的直接计算方法。

假设我们要计算一个由函数z=f(x, y)所定义的三维曲面与xy平面围成的体积V。

为了计算这个体积，我们将其划分成n个小立方体，每个小立方体的体积可以近似看作dV=Δx×Δy×Δz。

那么整个体积V可以通过对每个小立方体的体积进行求和得到，即V = ∫∫∫dV = ∫∫∫f(x,y)dxdydz,其中∫∫∫表示对整个三维空间的积分。

我们可以先对z方向进行积分，然后对y方向进行积分，最后对x方向进行积分。

这个积分过程可以通过数值积分的方法进行近似计算。

二、柱坐标系下的变量变换方法直角坐标系下的直接计算方法在计算一些特殊形状的物体时可能不太方便，这时可以采用柱坐标系下的变量变换方法。

柱坐标系与直角坐标系的关系可以表示为x=r*cosθ，y=r*sinθ，z=z，其中r表示点到z轴的距离，θ表示点在xy平面的极角。

在柱坐标系下，三重积分的计算公式为V = ∫∫∫f(r*cosθ,r*sinθ,z)r dz dr dθ,其中r的取值范围为[0,∞)，θ的取值范围为[0,2π]。

在进行柱坐标系下的三重积分计算时，我们需要进行相关的变量替换和坐标范围的调整。

具体方法如下：1.将直角坐标系中的函数f(x,y,z)进行变量替换，将x、y、z用r、θ、z表示，并计算出新的函数F(r,θ,z)。

2.确定新的坐标范围，即r的取值范围、θ的取值范围和z的取值范围。

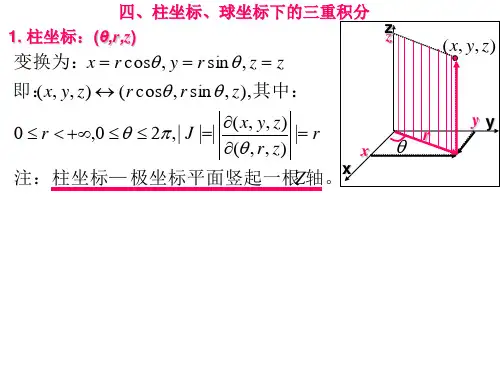
柱坐标、球坐标下的三重积分

解：由图知：直角系：
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系： I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分，
z
其中：z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标：(θ,r,z)
zz
变换为：x r cos , y r sin , z z
即：(x, y, z) (r cos , r sin , z),其中：
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注：柱坐标— 极坐标平面竖起一根Z轴。x
上顶： z 1 x2 y2
下底： z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标？柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注：用柱坐标求 fdv分成两个步骤：
第一步：先一后二，对z积分后将二重积分化为极坐标下的二重积分；
元素区域由六个坐标面围成：
半平面及+d ;
半径为r及 r+dr的园柱面；
平面 z及 z+dz；
dz

利用柱面坐标计算三重积分

`z
z
j r
zdv

dvΒιβλιοθήκη zdvO
dv

a 2 0 2
．
q
x
a y
dv 2 dj dq

2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、柱面坐标系的坐标面直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面直角坐标与球面坐标的关系、球面坐标系中的体积元素球面坐标系中的三重积分

，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲

面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解闭区域可表示为：
r 2z4，0r2，0q2．于是
zdxdydz zrdrdqdz

2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2

3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应，其中P(r, q )为点M在xOy面上的投影的极坐标．三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z

§9.5[1]利用柱面坐标和极坐标计算三重积分

再根据中 z,r,θ 的关系,化为三次积分. , , 的关系,化为三次积分. 积分. 一般, 积分, 一般,先对 z 积分,再对 r ,最后对 θ 积分.
例1 利用柱面坐标计算三重积分
∫∫∫ z dxdydz ,
其中其中
所围成的闭区域. 是由曲面 z = x2 + y2 与平面 z = 4 所围成的闭区域.
2
A
过 (r, θ )∈D 做平行于 z 轴 ∈ 的直线, 的直线,得
4
z
r2 ≤ z ≤ 4
0 ≤ θ ≤ 2π , : 0 ≤ r ≤ 2, 2 r ≤ z ≤ 4
o (r,θ )
x
y
即
r =2
o
2
于是, 于是,
A
∫∫∫ z dxdydz = ∫∫∫ z r drdθ dz.
= ∫0 dθ ∫0 dr∫r2 r z dz
规定: 规定:
z
0 ≤ r < +∞,
0 ≤ ≤π,
o θ
x
r
M( x, y, z)
y
0 ≤ θ ≤ 2π .
P
z
如图, 如图,三坐标面分别为
r 为常数
球
面;
r
为常数
θ 为常数
圆锥面; 圆锥面; 半平面.x来自zoθ
y
球面坐标与直角坐标的关系为
x = r sin cosθ , y = r sin sinθ , z = r cos.
= 2π ∫0 (Hr 3 r4 )dr
π H5 . =
10
二,利用球面坐标计算三重积分
设 M( x, y, z) 为空间内一点,则点M 可用三个有次为空间内一点, 来确定, 序的数r,,θ 来确定,其中r 为原点O 与点 M 间的距离, θ 轴正向所夹的角, 的距离, 为有向线段OM与z 轴正向所夹的角, 为从正z 轴来看自x 轴按逆时针方向转到有向线段 OP 的角,这里P 为点 M 在 xoy 面上的投影,这的角, 面上的投影, 的球面坐标. 样的三个数r,,θ 就叫做点M 的球面坐标.

三重积分的几种计算方法

*
例5. 计算 zdxdydz,
其中 ={(x, y, z) | x2+y2+z2≤1, z≥0}.
解：x2+y2+z2=1 r=1
z
用 = 截得 D()
而 0≤ ≤2 故
0
x
y
原积分
r cos r 2sindrdd
*
2
0 d
r 3cos sin drd
D ( )
z x 0
2
0 d
z
z=z2(x, y)
f (x, y, z)dxdydz
y
[ z2 (x,y) f (x, y, z)dz]dxdy
z=z1(x, y)
D z1 ( x, y)
D
y=y2(x)
0
a y=y1(x) b
x
设 D 为在 xy 平面上投影区域.
dxdy z2 (x,y) f (x, y, z)dz
z
x2 y2
.
4
y 原积分
a
r 2 r 2 sin drdd *
2
0 d
r 4sindrd
D( )
z
y
a
x
2
0 d
r 4sindrd
D( )
2
0
d
4
0
sin d
0ar
4dr
z
1a5 (2 2)
r=a
5
4
例7. 计算 f (x, y, z)dxdydz,表为球坐标系中的三次积分，其中为x2+y2+(z1)2≤1.
0
y= OPsin = rsin sin
yy
z= r cos

§6.3 三重积分的计算

解：将V 投影到z轴上得投影区间： 1 z 4 在(0, 4)内取一点z，过点(0, 0, z )
做平行x 0 y的平面截闭区域V , 得截面Dz : x y z ,
1
1
x2 2 y2 z 2 x2 2 2 1 x y 1 x 故V： 1 x 1
I dx
1
1
1 x 2 1 x
2
dy
2 x 2 x 2 y
2 2
f (x , y ,z )dz.
以上将三重积分化为三次积分是先计算一个定积分
V

x 2 y 2 dV ,其中V 是由不等式

z x 2 y 2， 1 z 4所确定的区域.
z 4
分析：如果采用先一后二法，对 z 积分的上下限情况怎样？
1 x y
例5 计算
V

x 2 y 2 dV ,其中V 是由不等式

z x 2 y 2， 1 z 4所确定的区域.
假设V中分布有体密度为 f (x,y,z)的某种物质，在Dxy上点(x, y)处取面积元素
d dxdy 以 d 的边界曲线为准线，作母线平行于z
轴的细长柱体，
d
该细长柱体可以看成以z为变量的细杆，它通过曲面 S1: z z1 ( x , y ) 进入区域V，然后，通过曲面 S2 : z z2 ( x , y ) 穿出区域V外，其进入点与
V V
z 1 r
2
z 1 x2 y2

2
0
d rdr
0
1
1 r 2 0
zdz
1 1 2 d r 1 r 2 dr 0 2 0

高等数学利用球坐标计算三重积分

D
xD
y
17
例1. 求由曲面 z x2 y2 与 z 2 ( x2 y2 )
所围立体的体积 V .
提示: 先求曲面的交线在 xoy 面上的投影域 D.
由
z x2 y2
z 2 ( x2 y2 )
z2 2 ( x2 y2 ) 2 z
消去 z 得D 的边界 x2 y2 1
和
所围成的体积 V 和表面积 S .
解: (1) 易求出
利用二重积分,得
30
(2)
31
所截
A
D
1
zx2
z
2 y
dxd y
D 1 x2 y2 dxdy
2
d
R
1 r 2 r dr
0
0
2
[ (1
R
2
)
3 2
1) ]
3
26
例2 求球面 x2 y2 z2 a2，含在圆柱体 x2 y2 ax内部的那部分面积.
解由对称性知 A 4A1,
D1： x2 y2 ax ( x, y 0)
z0
V (z2 z1)d D (2 r2 r2)rdrd
z1 x2 y2 o
1y
x
D
2
d
2
2
1r3dr 0
2
18
D
例2. 求球体 x2 y 2 z 2 R2与 x2 y 2 z 2 2Rz
公共部分体积.
解：求两球交线的投影. 由
x2 y2 z2 R2
x2 y2 z2 2Rz 消去 z 得 x2 y2 3 R2 D
dv r2 sin drd d
5
5
例3. 设由锥面
和球面

三重积分柱面球面坐标

0

d
.
y
rcos ) r 2 sin drdd
x
19
目录上页下页返回结束
f ( x, y, z)dxd ydz
F (r , , ) r 2 sin d r d d

其中 F (r , , ) f (r sin cos , r sin sin , r cos )
第三节三重积分
一、三重积分的概念二、三重积分的计算
第十章
1
目录上页下页返回结束
利用柱面坐标计算三重积分。
2
目录上页下页返回结束
2. 利用柱面坐标计算三重积分。
回忆用投影法（先一后二）计算三重积分
z2 ( x , y )
1
f ( x, y, z)dV dxdyz ( x, y )
球面坐标下的体积元素
z
元素区域由六个坐标面围成：半平面及+d ；半径为r及r+dr的球面；圆锥面及+d
rsind
dV = r 2 sin drdd
dV
r

f ( x , y, z )dxdydz
f (r sin cos , r sin sin ,
适用范围:
1) 积分域表面用球面坐标表示时方程简单; 2) 被积函数用球面坐标表示时变量互相分离.
20
目录上页下页返回结束
下面介绍一些区域的球面坐标的描述
21
目录上页下页返回结束
直角坐标球体
球面坐标
: x 2 y 2 z 2 R2
: 0 2 0 0r R

利用柱面坐标和球面坐标求积分

: r z a,
2 2
0 r a,
0 2 ,
2 a a
I ( x y )dxdydz d rdr r 2dz

0
0
r
5 a4 a5 3 2 r (a r )dr 2[a ] a . 0 4 5 10

_______________________；其值为__________.
二、计算下列三重积分: 2 2 1、 ( x 2 y 2 )dv ,其中是由曲面4z 2 25( x y ) 及平面 z 5 所围成的闭区域.

2、 ( x 2 y 2 )dv ,其中由不等
dxdydz ,

V d d
0 0
2
4
2a
0
r 2 sin dr
2
4 0
4 ( 2a )3 3 sin d ( 2 1)a . 3 3
补充：利用对称性化简三重积分计算
使用对称性时应注意：１、积分区域关于坐标面的对称性；２、被积函数在积分区域上的关于三个坐标轴的奇偶性．

d d
0
2
4 0
a cos 0
r sin dr
4 3
2
4 0
1 a5 sin 3 ( 5 0)d 5 cos
5 a . 10
解2
采用柱面坐标
D : x2 y2 a2 ,
x2 y2 z2 z r ,

0 a x 2 y 2 z 2 A, z 0 所确定. x2 y2 z2 3、 ( 2 2 2 )dxdydz , a b c x2 y2 z2 其中 ( x , y , z ) 2 2 2 1 . a b c 2 2 三、求曲面 z 5 x 2 y 2 及 x y 4 z 所围成的立体的体积. 2 x 2 y az 4a 2 将球体 x 2 y 2 z 2 4az 分四、曲面成两部分,试求两部分的体积之比. 五、求由曲面 z x 2 y 2 , x y a , x 0, y 0, z 0 所围成立体的重心(设密度 1 ).

9.5_三重积分计算2

一般地，先对，后对r，一般地，先对z，后对，最后对 θ 积分
二、利用球面坐标计算三重积分
z
设 M ( x, y, z ) 为空间内一点，则点 M 可用三个有次序的数r，
A
x
r
M ( x,
z
y, z )
o
P ，θ 来确定，其中 r 为原点 O 与 x 点 M 间的距离，为有向线段 OM 与 z轴正向所夹的角，θ 为从正 z 轴往下看自 x 轴按逆时针方向转到有
0
π 2 0
π 2 0
R
x
.
例 4、求曲面 x2 + y2 + z2 ≤ 2a2与 z ≥ x2 + y2 成的立体体积. 所围成的立体体积
解
由x
2
由锥面和球面围成，采用球面坐标，由锥面和球面围成，采用球面坐标，
+ y + z = 2a
2 2
2 2
2
r = 2a ,
z=
π x + y = , 4
z
M ( x,
∞ < z < +∞ .
x = r cos θ , 直角坐标与柱面坐标的关系为 y = r sin θ , z = z.
o
θ
y, z )
r
P (r ,θ )
y
x
柱面坐标的坐标面动点M( 动点 r, θ, z) z r =常数：圆柱面常数：常数圆柱面S z =常数：平面Π 常数：常数 S
‘
= abc ∫ dθ ∫ sin d ∫ 1 r 2 dr =
0 0 0
2π
π
1
π2
4
例7、计算∫∫∫ ( x + y + z ) cos( x + y + z ) 2 dxdydz

9-3(2)三重积分

3、在球面坐标系下将三重积分化为三次单积分
主要有两种情况：
1° 的边界曲面是一个包围原点在内的闭曲面。
曲面坐标为r r ( , )
则 I d d
0 0 2

r ( , )
0
F ( r , , )r 2 sindr
其中 : F ( r , , ) f ( r sin cos , r sin sin , r cos )
rsind
半径为r及r+dr的球面；
dV
r

圆锥面及+d
dv r sindrdd ,
2
f ( x, y, z )dxdydz

0

d
y
2 f ( r sin cos , r sin sin , r cos ) r sindrdd .
dz
dV
平面 z及 z+dz；
dV = rdrddz
f ( x , y , z )dxdydz
.
z
0
d
r
y
f ( r cos , r sin , z ) r drddz

x
底面积：r drd
3、在柱面坐标系下将三重积分化为三次单积分
次序通常选择为z ，r ，
0
r dr z dz
2 0
a
2 d
0

2 cos
0
2 2 cos z a 2 2 r dr 2 d r dr 0 0 2 2 0
2 8 a 8a 2 3 d cos d 9 6 0
2 a
a 2
2
r 2 0 3 0

(整理)在柱坐标系下三重积分计算法的探讨.

在柱坐标系下三重积分计算法的探讨‘计算三重积分的基本方法是将三重积分转化隽三次单积分进行计算，{l{；转诧过程在妻熊坐标系、柱坐标系和球坐标系下均可进行。

对在直角坐标系下如何转化的问题，笔者已在文¨几珏1中进行过讨论，而在柱坐标系和球坐标系下且易画出积分区域草网的情形，一般教材中都有。

因此，本文着重讨论在柱坐标系下且不易画趱积分区域草图的情形嚣量，如傅将三重积分转化为柱坐标系下三次单积分的阕题。

由于在转化过程中最关键的地方是如何确定单积分的上下限，即如何用柱坐标将积分区域用不等式组表出。

所以，为能较好地理解在柱坐标系下化三熏积分为三(累)次积分的公式，下面先介绍“卜型区域”、“足一墅区域”穰“歇移一型区域”、“Z醐_型区域”的概念。

1 0--型区域和JR一型区域(1)Ell不等式组fa置、口囊p ，、给出的平面区域(图1)Lrl(秽，燕r S r2‘一)D={(r，参)l^(参)黑r≤r2(移)，g≤0蕊零}称为护型区域，其中1(0)、r2(0)是(伐，卢]上的单值连续踊数。

卜型区域D的几何特征：1)逸域D壶连续趣线r=^(拶)(称为里边界线)，，=r2(拶)(称隽外边界线)及射线拶=痿与拶；届所围成；．2)从极点出发经过D内部的射线与D的边界曲线的交点不多于两点(图1)。

(a)(一般情形))0=伐圈1 0一型区域Fig．I Region of 0·-type(b)(特殊情形)·收稿日期：2008—04—22终毒簦会：薹艳梅《1963一)，女，云篱省昆羁泰入，捌教授，主要从事基础数学教学王佟。

0=伐万方数据第1期董艳梅．等：程柱坐标系下三重积分计算法的探讨·73·(2)由不等式组l口(7)≤o爆05(7’给出的平面区域(图2)埝≤rl S r g砭D={(r，一)1 0蠛rt s r蝶如，01(r)蠖秽s 02(r)}称为置一型隧域，其中0，(，．)、眈(r)是[r，，r2]上的单值连续函数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考：思考：是否可考虑用切片法来求解？

例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法直角坐标系(切片法)
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
解
(V )向xoy面投影(σ xy )为圆 : 0 ≤ ρ ≤ R, 0 ≤ θ ≤ 2π
y
(σ xy )
x
此时0 ≤ z ≤ R 2 − ρ 2 .
∴ I = ∫∫(σ ) [ ∫0
xy
R2 −ρ 2
zρdz ]dρdθ
2、体积元素、
当用三族坐标面来划分 (V ) : ρ = ρ , ρ = ρ + dρ ;
z
z = z , z = z + dz;
则体积元素
θ = θ , θ = θ + dθ ;
dv dz
o x
dθ
y
dρ
dv = ρdθdρdz
(V )
∴ ∫∫∫
f ( x, y , z )dv = ∫∫∫(V ) f ( ρ cosθ , ρ sin θ , z ) ρdρdθdz.
∫∫∫
(V )
f ( x, y, z )dv = ∫∫∫
(V )
f ( ρ cosθ , ρ sin θ , z ) ρdρdθdz.
3、化为累次积分、
z 2 ( ρ ,θ )
设区域(V ) : 在xoy面投影域为(σ ) :
（投影域用极坐标表示）
z
• •
z1 ( ρ ,θ )
z1 ( ρ ,θ ) ≤ z ≤ z 2 ( ρ ,θ ).
其中x, y与ρ ,θ之间关系为 :
1、柱面坐标在直角坐标系中,当xoy面上点用极坐标表示时、
z
x = ρ cos θ , y = ρ sin θ
,z = z
•
P
z
o
以z 当ρ = 常数：轴为中心轴的圆柱面； x
θ
ρ
• P′
y
过z 当θ = 常数：轴的半平面；当z = 常数：垂直于z轴的平面；
3、化为累次积分、
z ρ = ρ 2 (θ , ϕ )
• •
ρ = ρ1 (θ , ϕ )
(1)用x = ρ sin ϕ cos θ , y = ρ sin ϕ sin θ , z = ρ cos ϕ
化被积函数为球坐标系下形式ρ = ρ (θ , ϕ );
(2)任取θ、ϕ作一射线交 (V )于两点， x
y
o
则∫∫∫
(V )
•σ
f ( ρ cosθ , ρ sin θ , z ) ρdρdθdz
z 2 ( ρ ,θ )
1
( ρ ,θ )
x
= ∫∫ [ ∫z ( ρ ,θ ) (σ )
f ( ρ cosθ , ρ sin θ , z ) ρdz
]dρdθ
例1 计算三重积分I = ∫∫∫ zdv,
(V )
(σ z ) : x + y ≤ 2 z − z ; 0 ≤ z ≤ 2.
2 2 2
1
∴ I = ∫ ∫∫ zdσ dz 0 (σ z )
2
o x
y
= ∫ zσ z dz
0
2
= ∫ zπ ( 2 z − z )dz
2 0
2
4π = . 3
解法2 解法柱面坐标系计算
∫∫∫ zdv
1、球面坐标、
球面坐标系下三重积分的计算 z
•
在球面坐标系中, 空间点P ( x, y, z )用 ( ρ ,θ , ϕ )表示. 其中r = ρ sin ϕ ∴ x = r cos θ = ρ sin ϕ cos θ , y = r sin θ = ρ sin ϕ sin θ .
P
o x
θ
ϕ ρ z
y
∴ I = ∫ dθ ∫
0
2π
π /2
0
dϕ
5
∫
2 cosϕ
x
= 2π ∫
π /2
0
4π . 4 cos ϕ sin ϕdϕ = 3
0
本讲主要内容
三重积分在柱面及球坐标系下的计算三重积分在柱面及球坐标系下的计算在柱面及球
（1）三重积分在柱坐标系下的计算；（2）三重积分在球坐标系下的计算；（3）举例；
2011-8-5
4-2-1
柱面坐标系下三重积分的计算
对应空间点P ( x, y , z )可用( ρ ,θ , z )表示.
0
1 4 = πR . 4
例4 计算三重积分I = ∫∫∫(V ) ( x + y + z )dv,
2 2 2
z
其中(V )由z = R 2 − x 2 − y 2 与 z = x 2 + y 2 所围.
分析 (V )为由半球面与锥面所围,
ϕ
故可用球面坐标,
此时,0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
dv
dρ
θ = θ , θ = θ + dθ ; ϕ = ϕ , ϕ = ϕ + dϕ
ϕ
o x
则体积元素dv : dv = ρ sin ϕdθ ⋅ ρdϕ ⋅ dρ
dϕ
ρ
y
dv = ρ sin ϕdθdρdϕ
2
∴ ∫∫∫
(V )
f ( x, y , z )dv
(V )
= ∫∫∫
f ( ρ sin ϕ cosθ , ρ sin ϕ sin θ , ρ cos ϕ ) ρ 2 sin ϕdρdθdϕ .
o
y
即得单积分：
(3)再对ϕ、θ作积分.
∴ ∫∫∫
(V )
f ( x, y , z )dv =
ϕ2
ρ 2 (θ ,ϕ )
1
∫θ
θ2
1
dθ ∫ dϕ ∫ρ (θ ,ϕ ) f ( ρ sin ϕ cosθ , ρ sin ϕ sin θ , ρ cos ϕ ) ρ 2 sin ϕdρ
ϕ1
例3 计算三重积分I = ∫∫∫ zdv,
z = ρ cos ϕ
P′
r
•
y
其中0 ≤ ρ < +∞, 0 ≤ θ ≤ 2π , 0 ≤ ϕ ≤ π .
当ρ = 常数：中心在原点的球面；
当θ = 常数：过z轴的半平面；
当ϕ = 常数：顶点在原点，中心轴为z轴的圆锥面；
2、体积元素、
z
dθ
当用三族坐标面去划分 (V ) : ρ = ρ , ρ = ρ + dρ ; ρ sin ϕ
0 ≤ θ ≤ 2π
h
•
此时, ρ 2 ≤ z ≤ h.
•
o
•
∴ I = ∫∫(σ ) [ ∫ρ ρ ρdz ]dρdθ
h 2
2
y
(σ xy )
xy
x
= ∫ dθ ∫ ( ρ h − ρ ) dρ
3 5 0 0
2π
h
1 3 = πh . 6
思考：思考：本题是否也可考虑用切片法来求解？
4-2-2
(V )
z
ϕ
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
分析 (V )为由半球面与xoy面所围, 故可用球面坐标,
θ
y
x
此时,0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
π
2
R
,0 ≤ ρ ≤ R.
∴ I = ∫ dθ
0
2π
∫
π /2
0
dϕ ∫ ρcosϕ ⋅ ρ 2sinϕ dρ
(V )
z
2
•
x 2 + y 2 + ( z − 1) 2 = 1
xoy面上投影为(σ xy ) : x 2 + y 2 ≤ 1;
则z的范围 :
1− 1− ρ2 ≤ z ≤ 1+ 1− ρ2.
1
o x
• •
y
σ xy
∴ I = ∫ dθ ∫ dρ
0 0
2π
1