当前位置：文档之家 › 柱面坐标系和球面坐标系求三重积分

柱面坐标系和球面坐标系求三重积分

  • 格式：ppt
  • 大小：562.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

三重积分在柱面及球坐标系下的计算

三重积分在柱面及球坐标系下的计算


= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考： 思考：是否可考虑用切片法来求解？

例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习 试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法 直角坐标系(切片法)
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法 球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
柱面坐标系和球面坐标系求三重积分

柱面坐标系和球面坐标系求三重积分


z x2 y2所围 .
分析 (V )为由半球面与锥面所围,
故可用球面坐标,
y
此 ,0 时 2 ,0 ,0R . x
4
2
I d
/4
d
R22sind
0
0
0
2 2 R5.
5
练习 试用三种坐标系算 分三 别重 计积分
I zdv,其中(V): x2 y2 z2 2z. (V)
解法1 直角坐标(切 系片法 )
x
则 (V )f(c o,s si,n z)d d dz ,
]d d
[ z2(,)f(co ,ssin,z)dz
( ) z1(,)
例1 计算三重积I分 (Vz)dv,
其中(V)由z R2 x2 y2与 z 0所围.
解 (V )向 xo 面 y 投 (x)y 为 影 :0 圆 R , 02 x
I d d
zdz
0
0 1 1 2
x
2012 12d
4 . 3
•1
xy
解法3 球面坐标系计算zdv (V) x2y2z22z
z
2
球面 : 为 2co,s其中
02 ,0,02co .s
2
o
y
I 2d /2d 2coscos2sxind
0
0
0
2/24co5ssind 4 .
0
3
z
h•
此,时 2zh.
I [ h 2dz ]dd ( xy ) 2
•
o•
x
y
( xy )
2d h(3h5)d
0
0
1 h3.
6
思考：本题是否也可考虑用切片法来求解？
4-2-2 球面坐标系下三重积分的计算
三重积分计算法

三重积分计算法


如图,将 设 如图 将 向xoy面投影， 面投影 得 D xy ,以 D xy 的边界为准 以 线母线平行于z轴的柱面 线母线平行于 轴的柱面 分为下上两个边界： 把 分为下上两个边界：
O

z
z = z2 ( x, y) z2 S2
z = z1 ( x , y ) , z = z2 ( x , y )
0
xdz
= ∫ dx ∫
0
1 0
D 1
= ∫ xdx ∫
1 x 2 0 1 x 2 0
dy ∫
1 x 2 y
0
xdz
(1 x 2 y )dy
1 1 1 2 3 = ∫ ( x 2 x + x )dx = 4 0 48
例2 将 ∫∫∫ f (x, y, z)dv 化为直角坐标系下的
三次积分， 三次积分，其中 是由平面 x＋y＋z＝1， ＋ ＋＝ ， x＋y＝1，x＝0，y＝0，z＝1围成的区域。 ＋ ＝ ， ＝ ， ＝ ， ＝ 围成的区域 围成的区域。 解 ， 的投影 Dxy 是x+y=1， y
Dρθ
1(
2 ( ρ,θ )
, )
f (ρ cosθ, ρ sinθ, z)dz
若 Dρθ : ρ1 (θ ) ≤ ρ ≤ ρ2 (θ ) , α ≤ θ ≤ β 则三重积分化为柱面坐标的三次积分：
∫∫∫ f ( x, y, z )dv
= ∫ dθ ∫
α
β
ρ 2 (θ ) ρ1 (θ )
ρd ρ ∫
∫∫∫ f ( x , y, z )dv = ∫∫ [∫
Dxy
z2 ( x , y ) z1 ( x , y )
f ( x , y , z )dz ]dxdy
利用柱面坐标计算三重积分精编版

利用柱面坐标计算三重积分精编版


cos
4
I ( x2 y2 )dxdydz


2
d

4 d
a
cos r 4 sin 3dr
0
0
0

2
4 0
sin
3


1 5
(
a5 cos5

0)d
a5. 10
解 2 采用柱面坐标
x2 y2 z2 z r, D : x2 y2 a2,
规定： 0 r , 0 , 0 2.
如图，三坐标面分别为
r 为常数
为常数 为常数
球 面； 圆锥面； 半平面．
如图，
z
设点 M 在 xoy 面上的投影为P，
r M(x, y,z)

点 P 在 x 轴上的投影为 A，
z
则 OA x, AP y, PM z.
用哪种坐标？柱面坐标 1
锥面化为: r = z
上顶： z = 1
下底： z r
Dxy: r 1
Dxy
0
....
x
1y
11
I


D
rdrdθ
r
r2

dz 1
2π
1r
1
0 dθ 0 r 2 1 dr r dz
2π
1 1 r
0
( 1

r
2
1)dr

(ln2 2 )
二、利用球面坐标计算三重积分
设 M(x, y, z) 为空间内一点，则点M 可用
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
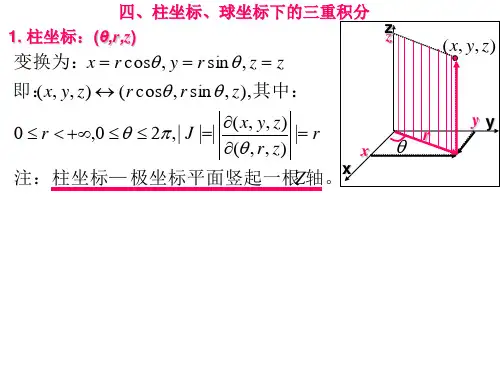
柱坐标、球坐标下的三重积分

柱坐标、球坐标下的三重积分


解：由图知：直角系：
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系： I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分，
z
其中：z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标：(θ,r,z)
zz
变换为：x r cos , y r sin , z z
即：(x, y, z) (r cos , r sin , z),其中：
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注：柱坐标— 极坐标平面竖起一根Z轴。x
上顶： z 1 x2 y2
下底： z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标？ 柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注：用柱坐标求 fdv分成两个步骤：
第一步：先一后二，对z积分后将二重积分化为极坐 标下的二重积分；
元素区域由六个坐标面围成：
半平面及+d ;
半径为r及 r+dr的园柱面；
平面 z及 z+dz；
dz
柱面坐标和球面坐标计算定积分

柱面坐标和球面坐标计算定积分

一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
利用柱面坐标和球面坐标计算三重积分

利用柱面坐标和球面坐标计算三重积分


2
D2 : x2 y 2 4, 2 :
D1 D2
0 2
0 r 2
r
2
z
. 2
2
I I1 I2
( x2 y2 )dxdydz ( x2 y2 )dxdydz,
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
3.5 利用柱面坐标和球面坐标 计算三重积分
一、利用柱面坐标计算三重积分 二、利用球面坐标计算三重积分
三、小结
一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
圆柱面；
z
为常数
z 为常数
半平面； 平 面．
• M (x, y, z)
z
柱面坐标与直角坐 标的关系为
or
• P(r, )
y
x r cos ,
y
r
sin
,
x
z z.
如图，柱面坐标系 中的体积元素为
x2 y2 z2， 与平面z a (a 0) 所围的立体.
解: 采用球面坐标
za r a , cos
x2 y2 z2 ,
4
: 0 r a , 0 , 0 2,
利用柱面坐标计算三重积分

利用柱面坐标计算三重积分

`z
z
j r
zdv

dvΒιβλιοθήκη zdvO
dv

a 2 0 2
．
q
x
a y
dv 2 dj dq


2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分

，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲

面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz

2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2

3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
谈谈三重积分的定限方法

谈谈三重积分的定限方法

谈谈三重积分的定限方法计算三重积分的基本方法是将三重积分化为三次积分来计算，而这里的一个关键问题是如何根据积分区域Ω来定限，下面分别介绍一下利用直角坐标，柱面坐标，球面坐标计算三重积分时如何定限的方法。

一、利用直角坐标计算三重积分时如何定限？ 教材中将积分区域Ω表示为:}),()(:),(),,(),(),,{(2121b x a x y x y x y x z y x z y x yy D zz xy ≤≤≤≤∈≤≤=Ω(1)从而将三重积分化为三次积分为：⎰⎰⎰⎰⎰⎰Ω=D z z dz z y x f dxdy dv z y x f xyy x y x ),(),(21),,(),,(=dz y y z z z y x f dy dx x x y x y x ba ⎰⎰⎰)()(),(),(2121),,(这个公式也称为“先一后二”积分公式。

（上述公式是将Ω向xoy 平面投影得到的，将Ω向其他坐标平面投影可得到类似的公式）当积分区域的几何形体较简单时，容易写出Ω的集合表达式（1），但积分的区域的立方图形通常难以画出,因此确定Ω的集合表达式（1）较困难。

为了解决这个困难。

下面介绍一个所谓“求围定顶”的定限法：称（1）式中),(1y x z ，),(2y x z 分别为区域Ω的下顶和上顶，以D xy 的边界曲线为准线，母线平行于Z 轴的柱面，位于下顶和上顶之间的部分称为Ω的“围墙”，Dxy的边界曲线称为“围线”，（它是投影柱面与xoy 平面的交线），下面分三种情况来介绍“求围定顶”的定限法。

1.设Ω由曲面),(y x h z =与),(y x g z =围成，不出现“围墙”，此时两曲面的交线在xoy 平面上的投影即为“围线”。

例 1.化三重积分⎰⎰⎰Ωυd z y x f ),,(为三次积分，其中Ω为由曲面2222,2x z y x z -=+=围成的闭区域例：“求围” 由方程组{22222xz y x z -=+=消去z 得两曲面交线在xoy 平面上的投影，即“围线”：122=+y x ，因此1:22≤+y x D xy ，即 .11,11:22≤≤--≤≤--x x y x D xy“定顶” 在Dxy内任取一点代入两曲面方程),(y x h z =，),(y x g z =得到两个z 的值，大者为上顶，小者为下顶。

柱面坐标系

柱面坐标系


π 0≤≤ , 4
0 ≤ θ ≤ 2π ,
zdv = ∫ dθ ∫ 4 d ∫ r cos r 2 sin dr ∫∫∫ 0 0 0
2a
2π
π
= 2π ∫
=
π
π
2
4 0
4
1 2a sin cos d |0 4
a
例 4 计算 ∫∫∫ x + y + z dv , 其中 由 x + y + z = z
:r ≤ z ≤ a, 0 ≤ r ≤ a, 0 ≤ θ ≤ 2π ,
I = ∫∫∫ ( x + y )dxdydz = ∫ dθ ∫ rdr ∫ r 2 dz 0 0 r
2 2
2π
a
a
a a π 5 = 2π ∫0 r (a r )dr= 2π [a ] = a . 4 5 10
a
4
5
3
补充：利用对称性化简三重积分计算
( x 2 + y 2 + z 2 )dv ∫∫∫
在球面坐标系下 为
0 ≤ θ ≤ 2π , 0 ≤ ≤ π , 0 ≤ r ≤ 2.
∴ I = ∫0 dθ ∫0 d ∫0 r r sin dr
2 2 2
2π
π
= 2π ∫0 sin d ∫0 r dr
2 4
π
16 = 2π . 5
五、小结
使用对称性时应注意： 使用对称性时应注意： 积分区域关于坐标面的对称性； １、积分区域关于坐标面的对称性； ２、被积函数在积分区域上的关于三个坐标轴 的奇偶性． 的奇偶性．
一般地， 平面对称， 一般地，当积分区域 关于xoy平面对称， 的奇函数， 且被积函数 f (x, y, z)是关于 z的奇函数，则三 重积分为零， 重积分为零，若被积函数 f (x, y, z)是关于 z的 偶函数， 上方的半个闭 偶函数， 则三重 积分为在xoy平面 上方的半 个闭 区域的三重积分的两倍. 区域的三重积分的两倍.
柱面坐标系.

柱面坐标系.


I 0 d 0 d 0 r r sin dr
2 2
2


2
2 0 sin d 0 r dr
4

2
16 2 . 5
五、小结
三重积分换元法
柱面坐标 球面坐标
（1） 柱面坐标的体积元素
dxdydz rdrddz
（2） 球面坐标的体积元素
dxdydz r sin drdd
则 OA x , AP y, PM z .
A
r

M ( x, y, z )
z
o

球面坐标与直角坐标的关系为
x
y
P

y
x r sin cos , y r sin sin , z r cos .
四 利用球面坐标计算三重积分
z
球面坐标系中的体积元素为
2


2



4 0
4
1 2a sin cos d |0 4
2
a
由x y z z 例 4 计算 x y z dv , 其中
2 2 2
2 2 2

2 2 2 x y z 2 z 所围空间闭区域． 和 为0 2 ,0 , cos r 2 cos ． 解 2
I ( x y )dxdydz d rdr r 2 dz 0 0 r
2 2
2
a
a
a a 5 2 0 r (a r )dr 2 [a ] a . 4 5 10
a
4 5

3
补充：利用对称性化简三重积分计算

高等数学随堂讲解三重积分在柱坐标与球坐标系下计算


一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
➢柱坐标系 平面极坐标系添加oz轴得到的空间坐标系
➢柱坐标 设 M (x, y, z) R3,
➢直角坐标与柱坐标的关系
x cos
点M的柱坐标
z
y sin
zz
z M (x, y, z)
规定
在柱坐标系下
常数 常数
圆柱面 半平面
o
y
x (x, y,0)
z 常数
平面
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
➢球坐标系下三重积分计算公式
f (x, y, z)dv f (r sin cos , r sin sin , r cos )r 2 sin drdd
二、三重积分在球坐标系下的计算
（一）球坐标系 （二）球坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
（一）球坐标系 （二）球坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法

柱面坐标系.

解 所围成的立体如图，
x2 y2 z2
z r,
D : x2 y2 1,
: r z 1, 0 r 1, 0 2 ,
所以 z x2 y2 dxdydz
zr 2drddz
2
d
1 r 2dr
1
zdz
0
0
r
2 1 r 2 (1 r 2 )dr
0
2
2 .
15
第四节 利用柱面坐标和球面 坐标计算三重积分
一 柱面坐标系 二 利用柱面坐标计算三重积分 三 球面坐标系 四 利用球面坐标计算三重积分 五 小结
一 柱面坐标系
设 M(x,y,z)为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,θ，则这样的三
个数 r,θ,z 就叫点 M 的柱面坐标．
区域的三重积分的两倍.
例 6 利用对称性简化计算
z
ln( x2 x2
y
y2 2
z
z2 2
1
1)
dxdydz
其中积分区域 {( x, y, z) | x2 y 2 z 2 1}.
解 积分域关于三个坐标面都对称，
被积函数是 z 的奇函数
z
ln( x2 x2
y
y2 2
z2 z2
1
例3 计算 zdv, 其中 是 x2 y2 z2 2a2 与
z x2 y2 所围成的立体.
解 由锥面和球面围成，采用球面坐标，
由 x2 y2 z 2 2a2
r 2a,
z x2 y2 ,
4 : 0 r 2a, 0 ,
4
0 2,
zdv
2
0
d
4 0
d
0

利用柱面坐标与球面坐标计算三重积分


f ( r cos , r sin , z )rdrddz.

rdrd
Dr
z2 ( r , ) z1 ( r , )
f ( r cos , r sin , z )dz .
通常化为先对 z、再对 r、后对θ 的三次积分.
先将Ω在xOy面上的投影域用极坐标不等式表示
设M(x, y, z)为空间内一点,记向量OM来自长为r , OM与z轴z

r
M ( x, y, z )
z
正方向间的夹角为 , 再将OM
A x
x
O

y

y
P
向xOy平面投影, 记投影向量与x轴正方向的 夹角为 , 称 ( r , , ) 为点M的球面坐标. 规定 0 r , 0 , 0 2 .
=常数: 半平面P
0

y
x
直角坐标与柱面坐标的关系为
x r cos , y r sin , z z.
在柱面坐标下 1. 若被积函数形如
x y r . 因此
2 2 2
f (x y ) ;
2 2
2. 积分区域Ω是由柱面、锥面、旋转抛物面、平 面或球面所围成.
y
球面坐标下的体积元素
z
元素区域由六个坐标面围成：
圆锥面
球面r+d r
半平面 及+d ； 圆锥面及+d
rsind
半径为r及r+dr的球面；
r
圆锥面+d
1
1
2 1dr 2 0 1 r
1
1 r
Dxy
0
1
y

9-3(2)三重积分


3、在球面坐标系下将三重积分化为三次单积分
主要有两种情况：
1° 的边界曲面是一个包围原点在内的闭曲面。
曲面坐标为r r ( , )
则 I d d
0 0 2

r ( , )
0
F ( r , , )r 2 sindr
其中 : F ( r , , ) f ( r sin cos , r sin sin , r cos )
rsind
半径为r及r+dr的球面；
dV
r

圆锥面及+d
dv r sindrdd ,
2
f ( x, y, z )dxdydz

0

d
y
2 f ( r sin cos , r sin sin , r cos ) r sindrdd .
dz
dV
平面 z及 z+dz；
dV = rdrddz
f ( x , y , z )dxdydz
.
z
0
d
r
y
f ( r cos , r sin , z ) r drddz

x
底面积 ：r drd
3、在柱面坐标系下将三重积分化为三次单积分
次序通常选择为z ，r ，
0
r dr z dz
2 0
a
2 d
0

2 cos
0
2 2 cos z a 2 2 r dr 2 d r dr 0 0 2 2 0
2 8 a 8a 2 3 d cos d 9 6 0
2 a
a 2
2
r 2 0 3 0

三重积分计算中投影坐标面的选择研究

三重积分计算中投影坐标面的选择研究三重积分是高等数学中的一种重要计算方法，它是通过对三维空间内的物理量进行求积分运算来实现的。

在进行三重积分运算时，必须选定一个合适的坐标系，并确定积分区域的投影坐标面，才能正确地计算出积分值。

本文将针对三重积分计算中投影坐标面的选择问题进行研究和探讨。

一、坐标系的选择在三重积分计算中，可选择笛卡尔坐标系、柱面坐标系和球面坐标系三种常见坐标系进行计算。

其中，笛卡尔坐标系是最为常用的坐标系，因为它的计算方法较为简单，容易掌握。

而对于涉及到圆柱体或球体等几何体的三重积分计算，柱面坐标系和球面坐标系更为适用。

柱面坐标系是一种三维平面直角坐标系，其中一条坐标轴沿圆柱体的轴线方向，另外两条坐标轴在圆柱体底面的圆上转动。

用柱面坐标系进行三重积分计算时，通过确定坐标轴方向，来选定积分区域的投影坐标面。

例如，对于一个长度为L，半径为R的圆柱体，假设其坐标轴方向为z轴，底面圆的投影坐标面为xy平面，则z轴垂直于xy平面，积分区域可以表示为0≤z≤L，0≤r≤R，0≤θ≤2π。

选定坐标系后，还需要确定积分区域的投影坐标面，以方便进行计算。

投影坐标面的选择应该遵循以下原则：1、计算直观明确。

选定的投影坐标面应使被积函数在相应坐标变量上具有简单的形式。

2、积分限简单。

选定的投影坐标面应使积分区域在该坐标面上的限制最为简单，例如，长方体的投影坐标面应当为xy平面。

3、减少积分数。

选定的投影坐标面应该减少积分变量的数量，从而减少计算量和运算难度。

在确定投影坐标面时，还要考虑积分区域的对称性和特殊形状等问题，以便通过使用对称性等技巧，来简化运算和降低误差。

综上所述，三重积分计算中投影坐标面的选择是十分重要的，它将直接影响到积分计算的结果和难度。

在进行三重积分计算时，需要根据具体问题选定合适的坐标系，并基于计算直观、积分限简单和减少积分数等原则，来选择投影坐标面，以准确、高效地完成积分计算任务。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、球面坐标 、
球面坐标系下三重积分的计算 z
•
在球面坐标系中, 空间点P ( x, y, z )用 ( ρ ,θ , ϕ )表示. 其中r = ρ sin ϕ ∴ x = r cos θ = ρ sin ϕ cos θ , y = r sin θ = ρ sin ϕ sin θ .
P
o x
θ
ϕ ρ z
(V )
z
2
•
x 2 + y 2 + ( z − 1) 2 = 1
xoy面上投影为(σ xy ) : x 2 + y 2 ≤ 1;
则z的范围 :
1− 1− ρ2 ≤ z ≤ 1+ 1− ρ2.
1
o x
• •
y
σ xy
∴ I = ∫ dθ ∫ dρ
0 0
2π
1
∫
1+ 1− ρ 2
2
1− 1− ρ
zρdz
(V )
z
ϕ
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
分析 (V )为由半球面与xoy面所围, 故可用球面坐标,
θ
y
x
此时,0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
π
2
R
,0 ≤ ρ ≤ R.
∴ I = ∫ dθ
0
2π
∫
π /2
0
dϕ ∫ ρcosϕ ⋅ ρ 2sinϕ dρ
2、体积元素 、
当用三族坐标面来划分 (V ) : ρ = ρ , ρ = ρ + dρ ;
z
z = z , z = z + dz;
则体积元素
θ = θ , θ = θ + dθ ;
dv dz
o x
dθ
y
dρ
dv = ρdθdρdz
(V )
∴ ∫∫∫
f ( x, y , z )dv = ∫∫∫(V ) f ( ρ cosθ , ρ sin θ , z ) ρdρdθdz.
∫∫∫
(V )
f ( x, y, z )dv = ∫∫∫
(V )
f ( ρ cosθ , ρ sin θ , z ) ρdρdθdz.
3、化为累次积分 、
z 2 ( ρ ,θ )
设区域(V ) : 在xoy面投影域为(σ ) :
（投影域用极坐标表示 ）
z
• •
z1 ( ρ ,θ )
z1 ( ρ ,θ ) ≤ z ≤ z 2 ( ρ ,θ ).
3、化为累次积分 、
z ρ = ρ 2 (θ , ϕ )
• •
ρ = ρ1 (θ , ϕ )
(1)用x = ρ sin ϕ cos θ , y = ρ sin ϕ sin θ , z = ρ cos ϕ
化被积函数为球坐标系 下形式ρ = ρ (θ , ϕ );
(2)任取θ、ϕ作一射线交 (V )于两点， x
y
∴ I = ∫ dθ ∫
0
2π
π /2
0
dϕ
5
∫
2 cosϕ
x
= 2π ∫
π /2
0
4π . 4 cos ϕ sin ϕdϕ = 3
0
y
o
则∫∫∫
(V )
•σ
f ( ρ cosθ , ρ sin θ , z ) ρdρdθdz
z 2 ( ρ ,θ )
1
( ρ ,θ )
x
= ∫∫ [ ∫z ( ρ ,θ ) (σ )
f ( ρ cosθ , ρ sin θ , z ) ρdz
]dρdθ
例1 计算三重积分I = ∫∫∫ zdv,
(V )
0
1 4 = πR . 4
例4 计算三重积分I = ∫∫∫(V ) ( x + y + z )dv,
2 2 2
z
其中(V )由z = R 2 − x 2 − y 2 与 z = x 2 + y 2 所围.
分析 (V )为由半球面与锥面所围,
ϕ
故可用球面坐标,
此时,0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
z = ρ cos ϕ
P′
r
•
y
其中0 ≤ ρ < +∞, 0 ≤ θ ≤ 2π , 0 ≤ ϕ ≤ π .
当ρ = 常数： 中心在原点的球面；
当θ = 常数：过z轴的半平面；
当ϕ = 常数：顶点在原点，中心轴为z轴的圆锥面；
2、体积元素 、
z
dθ
当用三族坐标面去划分 (V ) : ρ = ρ , ρ = ρ + dρ ; ρ sin ϕ
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法 球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
解
(V )向xoy面投影(σ xy )为圆 : 0 ≤ ρ ≤ R, 0 ≤ θ ≤ 2π
y
(σ xy )
x
此时0 ≤ z ≤ R 2 − ρ 2 .
∴ I = ∫∫(σ ) [ ∫0
xy
R2 −ρ 2
zρdz ]dρdθ
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习 试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法 直角坐标系(切片法)
= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考： 思考：是否可考虑用切片法来求解？
例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
0 ≤ θ ≤ 2π
h
•
此时, ρ 2 ≤ z ≤ h.
•
o
•
∴ I = ∫∫(σ ) [ ∫ρ ρ ρdz ]dρdθ
h 2
2
y
(σ xy )
xy
x
= ∫ dθ ∫ ( ρ h − ρ ) dρ
3 5 0 0
2π
h
1 3 = πh . 6
思考： 思考： 本题是否也可考虑用切片法来求解？
4-2-2
本讲主要内容
三重积分在柱面及球坐标系下的计算 三重积分在柱面及球坐标系下的计算 在柱面及球
（1）三重积分在柱坐标系下的计算； （2）三重积分在球坐标系下的计算； （3）举例 ；
作业： 作业：P215 2, 3, 4.
2011-9-30
4-2-1
柱面坐标系下三重积分的计算
对应空间点P ( x, y , z )可用( ρ ,θ , z )表示.
(σ z ) : x + y ≤ 2 z − z ; 0 ≤ z ≤ 2.
2 2 2
1
∴ I = ∫ ∫∫ zdσ dz 0 (σ z )
2
o x
y
= ∫ zσ z dz
0
2
= ∫ zπ ( 2 z − z )dz
2 0
2
4π = . 3
解法2 解法 柱面坐标系计算
∫∫∫ zdv
o
y
即得单积分：
(3)再对ϕ、θ作积分.
∴ ∫∫∫
(V )
f ( x, y , z )dv =
ϕ2
ρ 2 (θ ,ϕ )
1
∫θ
θ2
1
dθ ∫ dϕ ∫ρ (θ ,ϕ ) f ( ρ sin ϕ cosθ , ρ sin ϕ sin θ , ρ cos ϕ ) ρ 2 sin ϕdρ
ϕ1
例3 计算三重积分I = ∫∫∫ zdv,
dv
dρ
θ = θ , θ = θ + dθ ; ϕ = ϕ , ϕ = ϕ + dϕ
ϕ
o x

则体积元素dv : dv = ρ sin ϕdθ ⋅ ρdϕ ⋅ dρ
dϕ
ρ
y
dv = ρ sin ϕdθdρdϕ
2
∴ ∫∫∫
(V )
f ( x, y , z )dv
(V )
= ∫∫∫
f ( ρ sin ϕ cosθ , ρ sin ϕ sin θ , ρ cos ϕ ) ρ 2 sin ϕdρdθdϕ .
其中x, y与ρ ,θ之间关系为 :
1、柱面坐标 在直角坐标系中,当xoy面上点用极坐标表示时 、
z
x = ρ cos θ , y = ρ sin θ
,z = z
•
P
z
o
以z 当ρ = 常数： 轴为中心轴的圆柱面； x