华师版七年级数学角课课练

华东师大版数学初一上册第5章相交线与平行线55.1.3同位角、内错角、同旁内角同步课时练习题1. 如图，∠2和∠1是哪两条直线被哪一条直线所截形成的内错角()A．AD，BC被BD所截B．AB，CD被BD所截C．AB，AD被BD所截D．BC，DC被BD所截2. 如图，在所标识的角中，互为同位角的两个角是( )A．∠2和∠3 B．∠1和∠3 C．∠1和∠4 D．∠1和∠23. 如图，∠1和∠2是同旁内角的是( )4. 如图，能和∠α构成内错角的角的个数是( )A．1 B．2 C．3 D．45. 如图，有下列判定：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是( ) A．①②B．①②③C．②③④D．①②③④6. 如图，两直线AB，CD与直线EF，GH相交，图中的同旁内角共有( )A．4对B．8对C．12对D．16对7. 如图，∠B的同位角是_________，内错角是_________，同旁内角是__________和___________.8. 如图，在∠1，∠2，∠3，∠4，∠5，∠B，∠D，∠ACE中，与∠D是同位角的是______________；与∠2是内错角的是_________________.9. 如图，图中与∠E是同位角的有_________________，与∠D是内错角的有________________，与∠E是同旁内角的有_____________________ _，与∠D是同旁内角的有_______________.10. (1)如图，AB与BC被AD所截得的内错角是__________；(2)DE与AC被直线AD所截得的内错角是__________；(3)图中∠4的内错角是____和____.11. )(1)假如把下图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？(2)假如把下图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠2呢？12. 如图所示，假如内错角∠1与∠5相等，那么与∠1相等的角还有吗？与∠1互补的角有吗？假如有，请写出来，并说明你的理由．13. 如图所示，直线a，b被直线c所截，∠1＝40°，∠2＝105°，求∠1的同位角，∠4的内错角，∠3的同旁内角的度数．14. 如图，(1)∠B和∠FAC是什么位置关系的角？是哪两条直线被哪一条直线所截形成的？(2)∠C和∠DAC呢？∠C和∠FAC呢？(3)∠B的同旁内角分别是哪几个角？15．如图，直线AB，CD被EF所截，点G，H为它们的交点，∠1∶∠2＝5∶3，∠2与它的内错角相等，HP平分∠CHG.求：(1)∠4的度数；(2)∠CHP的度数．参考答案：1---6 BCDBB D7. ∠ACD ∠BCE ∠BAC ∠ACB8. ∠5和∠ACE ∠4和∠ACE9. ∠BAC和∠DAB ∠DAC和∠DAB ∠D，∠DAE，∠CAE ∠E，∠DAE10. (1) ∠1与∠3(2) ∠2与∠4(3) ∠5 ∠211. 解：(1)假如把图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对内错角，∠2与∠3是一对同旁内角(2)假如把图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对同位角，∠5与∠2是一对同旁内角12. 解：∠1＝∠2，与∠1互补的角有∠3和∠4，明白得：因为∠1＝∠5，∠5＝∠2，因此∠1＝∠2.因为∠1＝∠5，且∠5与∠3或∠4互补，因此与∠1互补的角有∠3和∠413. 解：∠1的同位角为∠4，而∠4＋∠2＝180°，因此∠4＝180°－∠2＝180°－105°＝75°；∠4的内错角∠5与∠1是对顶角，依照对顶角相等，∠4的内错角∠5＝∠1＝40°；∠3的同旁内角为∠4，因此∠3的同旁内角是75°14. 解：(1)观看∠B 和∠FAC 可知，直线FB 是截线，直线BC 和AC 是被截直线，现在∠B 和∠FAC 在截线FB 同一侧，被截线的同一方，故∠B 和∠FAC 是同位角(2)∠C 和∠DAC 是同旁内角，是直线DE 和BC 被直线AC 所截形成的．∠C 和∠FAC 是内错角，是直线FB 和BC 被直线AC 所截形成的(3)若直线BC 截直线AB 和AC ，则∠B 的同旁内角是∠C ；若直线AB 截直线AC 和BC ，则∠B 的同旁内角是∠BAC ；若直线AB 截直线DE 和BC ，则∠B 的同旁内角是∠EAB.因此∠B 的同旁内角有∠C ，∠BAC 和∠EAB15. 解：(1)∵∠1与∠2互补，∴∠1＋∠2＝180°.又∵∠1∶∠2＝5∶3，∴∠1＝112.5°，∠2＝67.5°.又∵∠4是∠2的内错角，∴∠4＝∠2＝67.5°(2)∵∠4与∠CHG 互补，∴∠CHG ＝180°－∠4＝112.5°.又∵HP 平分∠CHG ，∴∠CHP ＝12∠CHG ＝56.25°。

第1课时对顶角1.认识对顶角的概念，理解对项角主要反映了角的一种位置关系．2.能说出“对顶角相等”的性质，会用它进行有关的简单推理和计算。

1. 如果两个角有公共________，且其中一个角的两边分别是另一个角两边的________，则这两个角叫做互为对顶角．任意两个对顶角，它们都有一个相同的________角．2. 如果两个角是对顶角，那么这两个角______．简单地说成______________．3.如图所示，AB与CD相交于O，∠AOD+∠BOC=280°，则∠AOC为.4.如图，三条直线l1，l2，l3相交于点E，则∠1+∠2+∠3=（）A．90°B．120°C．180°D．360°5.下列语句正确的是（）A．若两个角是对顶角，则这两个角相等B．若两角相等，则这两个角是对顶角C．若两个角不是对顶角，则这两个角不相等D．以上判断都不对6. 如图所示，直线AB，CD相交于O，所形成的∠1，∠2，∠3，∠4中，下列分类不同于其它三个的（）A．∠1和∠2 B．∠2和∠3 C．∠3和∠4 D．∠2和∠47. 下列图形中，∠1与∠2是对顶角的是（）8.如图，直线AB，CD相交于点O，OA平分∠COE，∠COE=70°，则∠BOD的度数是（）A．20°B．30°C．35°D．40°9. ∠1的对顶角是∠2，∠2的邻补角是∠3，若∠3=45°，则∠1的度数是（）A．45°B．90°C．135°D．45°或135°10. 小明同学认为对顶角可以这样定义：顶点公共，而且相等的角叫对顶角，你认为正确吗？如果你认为不正确请举一个反例，并对“对顶角”正确定义．11. 如图，AB，CD交于O点．（1）如果∠AOD=3∠BOD，那么∠BOD= 度，∠COB= 度；（2）如果∠AOC=2x°，∠BOC=（x+90）°，∠BOD=（y+4）°，求x，y的值．12. 如图，当光线从空气中射入水中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射，在图中，∠1=43°，∠2=27°，试问光的传播方向改变了多少度？13. 以下说法正确的是（）A．有公共顶点，并且相等的两个角是对顶角B．两条直线相交，任意两个角都是对顶角C．两角的两边互为反向延长线的两个角是对顶角D．两角的两边分别在同一直线上，这两个角互为对顶角14. 三条直线两两相交于同一点时，对顶角有m对；交于不同三点时，对顶角有n对，则m 与n的关系是（）A．m=n B．m＞n C．m＜n D．m+n=1015. 用剪刀剪东西时，剪刀张开的角度如图所示，若∠1=25°，则∠2= 度．16. 一块直角三角板放在两平行直线上，如图所示，∠1+∠2= 度．17. 如图，直线AB、CD交于O点，且∠BOC=80°，OE平分BOC，OF为OE的反向延长线．（1）求∠AOD和∠AOF的度数；（2）OF平分∠AOD吗？为什么？18.如图所示，（1）是某城市古建筑群中一座古塔底部的建筑平面图，请你利用学过的知识设计如何测量出古塔外墙底部的∠ABC大小的方案，并说明理由．注：（2），（3）图备用．19. 如图，直线AB与CD相交于点O，OD恰为∠BOE的角平分线．（1）图中∠AOD的补角是（把符合条件的角都填出来）；（2）若∠AOD=140°，求∠AOE的度数．20. 如图所示是小明自制对顶角的“小仪器”示意图：（1）将直角三角板ABC的AC边延长且使AC固定；（2）另一个三角板CDE的直角顶点与前一个三角板直角顶点重合；（3）延长DC，∠PCD与∠ACF就是一组对顶角，已知∠1=30°，∠ACF为多少？21. 观察下列各图，寻找对顶角（不含平角）：（1）如图a，图中共有对对顶角；（2）如图b，图中共有对对顶角；（3）如图c，图中共有对对顶角；（4）研究（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成对对顶角；（5）若有2008条直线相交于一点，则可形成对对顶角．22. （2012•北京）如图，直线AB，CD交于点O，射线OM平分∠AOC，若∠BOD=76°，则∠BOM等于（）A．38°B．104°C．142°D．144°23.（2011•柳州）如图，在所标识的角中，互为对顶角的两个角是（）A．∠2和∠3 B．∠1和∠3 C．∠1和∠4 D．∠1和∠2第3课时1.顶点反向延长线补2. 相等对顶角相等3. 140°4.A5.A6.D7.D8.C9.C10. 解：不正确，如图，∠AOB=∠COD ，且其有公共的顶点O ，但不是对顶角．对顶角的定义：一个角的两边分别是另一个角的两边的反向延长线，这两个角叫对顶角．11. 解：（1）如果∠AOD=3∠BOD ，可以设∠BOD=x°，则∠AOD=3x°.∵∠AOD+∠BOD=180°，解得x=45，则∠BOD=45度，∠COB=135度；（2）已知∠AOC=2x°，∠BOC=（x+90）°，根据这两个角互补，得2x+x+90=180，解得x=30，∵∠BOD=∠AOC ，∴y+4=60，∴y=56．12. 解：若光路不发生改变，则∠BFD=∠1=43°，光路改变后，∠2=27°，则∠DFE=∠BFD-∠2=43°-27°=16°，所以光的传播方向改变了16°．13.C14.A15.2516.9017. 解：（1）∵∠AOD=∠BOC （对顶角相等），∴∠AOD=80°又∵OE 平分∠BOC ，∴∠BOE=21∠BOC=21×80°=40° 又∵∠AOF=∠BOE （对顶角相等），∴∠AOF=40°（2）OF 平分∠AOD∵∠AOD=80°，∠AOF=40°，∴∠FOD=80°-40°=40°，即∠AOF=∠FOD ，∴OF 平分∠AOD.18. 解：解法一：作AB 的延长线，量出∠CBD 的度数．∠ABC=180°-∠CBD （邻补角的定义）．解法二：作AB 和CB 的延长线，量出∠DBE 的度数就知道了∠ABC 的度数（对顶角相等）．19. 解：（1）由图示可得，∠AOD+∠AOC=180°，∠AOD+∠BOD=180°，又OD为∠BOE的角平分线，可得∠BOD=∠DOE，故∠AOD+∠DOE=180°，故∠AOD的补角是∠AOC、∠BOD、∠EOD；（2）∵∠AOD=140°，∴∠BOD=40°，∵OD为∠BOE的角平分线，∴∠EOD=40°，∴∠AOE=∠AOD-∠EOD=100°．20.解：∵∠PCD=90°-∠1，又∵∠1=30°，∴∠PCD=90°-30°=60°，而∠PCD=∠ACF，∴∠ACF=60°．21.（1）2；（2）6；（3）12；（4）()1-n n；（5）403005622.C23.A。

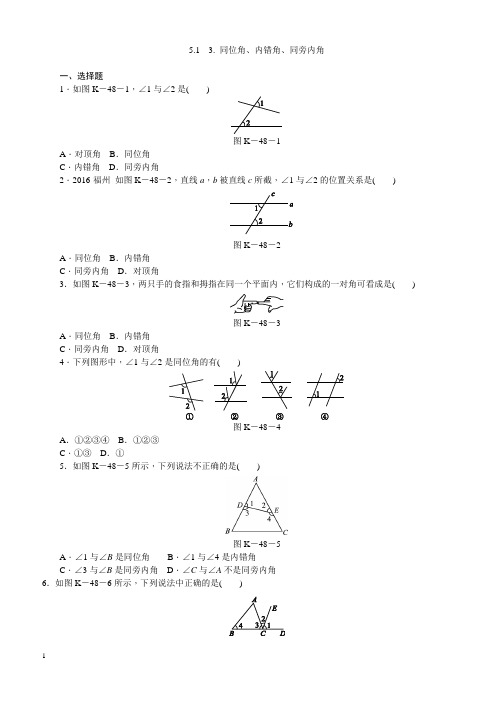
5.1 3. 同位角、内错角、同旁内角一、选择题1．如图K－48－1，∠1与∠2是()图K－48－1A．对顶角B．同位角C．内错角D．同旁内角2．2016·福州如图K－48－2，直线a，b被直线c所截，∠1与∠2的位置关系是()图K－48－2A．同位角B．内错角C．同旁内角D．对顶角3．如图K－48－3，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是()图K－48－3A．同位角B．内错角C．同旁内角D．对顶角4．下列图形中，∠1与∠2是同位角的有()图K－48－4A．①②③④B．①②③C．①③D．①5．如图K－48－5所示，下列说法不正确的是()图K－48－5A．∠1与∠B是同位角B．∠1与∠4是内错角C．∠3与∠B是同旁内角D．∠C与∠A不是同旁内角6．如图K－48－6所示，下列说法中正确的是()A．∠2和∠4是同位角B．∠2和∠4是内错角C．∠1和∠A是内错角D．∠3和∠4是同旁内角7．如图K－48－7所示，下列说法错误的是()图K－48－7A．∠1与∠2是同旁内角B．∠1与∠3是同位角C．∠1与∠5是内错角D．∠1和∠6是同位角8．如图K－48－8，CM，ON被AO所截，那么()图K－48－8A．∠1和∠3是同位角B．∠2和∠4是同位角C．∠ACD和∠AOB是内错角D．∠1和∠4是同旁内角9．如图K－48－9，与∠B是同旁内角的角有()图K－48－9A．1个B．2个C．3个D．4个10．如图K－48－10，图中的同位角的对数是()图K－48－10A．4 B．6 C．8 D．12二、填空题11. 如图K－48－11，∠ABC与________是同位角，∠ABC与________或________是同旁内角；∠ADB 与________或________是内错角．12．如图K－48－12所示，直线a，b被直线l所截，与∠1是同位角的是________，与∠1是内错角的是________，与∠1是同旁内角的是_________________________，∠1与________是对顶角．图K－48－1213．如图K－48－13，直线________和______被直线________所截，∠1和∠5是________角，∠1和∠6是________角，∠1和∠8是________角，∠1与∠3是________角，∠1与∠2是________角．图K－48－1314．如图K－48－14所示，直线AB，AC，CB两两相交，交点分别为A，B，C.则：(1)∠1和∠2是直线________和________被直线________所截得的________角；(2)∠1和∠3是直线________和________被直线________所截得的________角；(3)∠1和∠4是直线________和________被直线________所截得的________角．图K－48－1415．如图K－48－15所示，∠1与∠3是________角，∠3与∠4是________角，∠3与∠5是________角，∠2与∠4是________角．图K－48－1516．如图K－48－16所示，∠3与∠B是直线AB，______被直线________所截而成的________角；∠1与∠A 是直线AB，________被直线________所截而成的________角；∠2与∠A是直线AB，________被直线________所截而成的________角．图K－48－1617．如图K－48－17所示．(1)∠1与∠4是一对________角，具有同样位置关系的两个角还有________；(2)∠2与∠3是一对________角，具有同样位置关系的两个角还有____________.图K－48－1718．图K－48－18中，同位角有a对，内错角有b对，同旁内角有c对，则a＋b＋c的值是________．图K－48－18三、解答题19．如图K－48－19所示，直线a，b被直线c所截，∠1＝40°，∠2＝105°，求∠1的同位角、∠4的内错角、∠3的同旁内角的度数．图K－48－191．B 2.B 3.B4．C．5．D．6．D7.D8．B9．C10．D11．∠EAD∠BAD∠BCD∠DBC∠EAD12．∠3∠4∠2∠613．AB CD EF同旁内同位内错对顶邻补14．(1)AC BC AB同旁内(2)AC BC AB同位(3)AB BC AC同位15．对顶同旁内同旁内内错16．CE BD同位BC AC同旁内CE AC内错17．(1)内错∠3与∠4(2)同位∠1与∠218．1419．解：由图可知∠1 的同位角是∠4，而∠4＋∠2＝180°，因此∠4＝180°－∠2＝180°－105°＝75°. ∠4的内错角与∠1的对顶角是同一个角，根据对顶角相等，得∠4的内错角等于∠1，是40°.∠3的同旁内角是∠4，因此∠3的同旁内角是75°.。

相交线中的角【知能点分类训练】知能点同位角、内错角、同旁内角的概念1．如图1，（1）∠1和∠4是______角，∠1和∠3是_____角；（2）∠2和∠4是_____角；∠3和∠D是____角；（4）∠4和∠D是_____角，∠4和∠B是_____角．(1) (2) (3) (4)2．如图2，（1）∠ABC与∠______是同位角，∠ABC与∠_____是同旁内角；（2）•∠ADB与∠_____是内错角；（3）∠ABD与∠_____是内错角，∠ADC与∠____是内错角．3．如图3所示，∠1与∠2是______角，是直线______和直线______被直线_____•所截而形成的；∠1与∠3是______角，是直线_______和直线______被直线________•所截而形成的．4．如图4所示．（1）AD，BC被BD所截而成的内错角是___________；（2）CD，AE被AC所截而成的内错角是___________；（3）AD，BF被AE所截而成的同位角是___________；（4）BD，AE被AD所截而成的同旁内角是_________．5．如图5所示，若∠1=30°，∠2=110°，那么，∠3的同位角等于_______，∠3•的内错角等于______，∠3的同旁内角等于_______．(5) (6) (7)6．在下图中，∠1与∠2不是同位角的是（）．7．如图6，下列说法不正确的是（）．A．∠1与∠2是同位角; B．∠2与∠3是同位角;C．∠1与∠3是同位角; D．∠1与∠4是内错角8．如图7所示，下列判断正确的是（）．A．2对同位角，2对内错角，2对同旁内角;B．2对同位角，2对内错角，3对同旁内角;C．4对同位角，2对内错角，4对同旁内角;D．以上判断均不正确9．如图，四个图形中的∠1和∠2不是同位角的是（）．10．如图所示，图中同旁内角的对数是（）．A．15 B．27 C．30 D．39【综合应用提高】11．如图所示，请指出图中的同位角、内错角和同旁内角．12．两条直线被第三条直线所截，∠1是∠2的同旁内角，∠3是∠2的内错角，若∠1=3∠2，∠2=3∠3，求∠1，∠2的度数．13．如图所示，已知∠1=60°，∠2+∠3=180°，∠3=∠4，求∠5的度数．【开放探索创新】14．如图所示，直线AD与AE相交于A，直线BC分别交AD，AE于B，C，直线DE•分别交AD，AE于D，E，那么图中共有多少对同位角？答案:1．（1）邻补对顶（2）对顶同旁内（3）同位同位2．（1）EAD BAD或∠BCD （2）DBC或∠EAD （3）BDC EAD3．内错 AB BC AC 同旁内 AC BC AB4．（1）∠ADB与∠DBC （2）∠DCA与∠CAE（3）∠DAE与∠FBE （4）∠ADB与∠DAB5．70° 70° 110°点拨：∠3的同位角是∠2的邻补角，∠3的内错角也是∠2的邻补角，∠3的同旁内角是∠2的对顶角．6．C 点拨：C中，∠1与∠2的四条边分别在四条直线上．7．C 点拨：∠1与∠3的两条分别在四条直线上，不属于这三类角．8．B 9．C10．C 点拨：一个三角形中有3对同旁内角，一个四边形中有4对同旁内角，•图中共有5个三角形，6个四边形，但其中有9对重复出现，故共有30对同旁内角．11．如图所示，由图（1）知：∠A和∠DCE是同位角，∠A和∠ACD是同旁内角；由图（2）知：∠B和∠BCD是内错角．由图（3）知：∠A和∠BCE是同位角，∠B和∠BCE是内错角，∠A和∠B，∠A•和∠ACB，∠B和∠ACB分别是同旁内角．12．根据题意画出符合条件的图形，如图所示．∵∠1=3∠2，∠2=3∠3，∴∠1=9∠3．由图形可知，∠1+∠3=180°，∴9∠3+∠3=180°，∠3=18°，∴∠2=3∠3=3×18°=54°，∠1=3∠2=3×54°=162°．13．∵∠1+∠2=180°，∴∠1=60°，∴∠2=120°，又∵∠2+∠3=180°，∴∠3=60°．∵∠3=∠4，∴∠4=60°，又∵∠4+∠5=180°，∴∠5=120°．14．由探究评析中的分解图可知，图（1）中共有12对同位角，图（2）中共有12•对同位角，图（3）中共有4对内位角，图（4）中共有4对同位角，故图中共有12+12+4+4=32（对）同位角．。

一、单选题
1. 在同一平面上．∠AOB=60°，∠BOC=40°，则∠AOC等于（）
A．100°B．20°
C．100°或20°D．不能确定
2. 如图，辽宁省在河北省的（）
A．西偏南方向B．东偏北方向C．西偏北方向D．东偏南方向3. 在9点30分时，时钟上的时针与分针所夹的钝角是（）A．B．C．D．
4. 如图，在两处观测到的处的方位角分别是（）
A．北偏东，北偏西B．北偏东，北偏西
C．北偏东，北偏西D．北偏东，北偏西
5. 如图，轮船航行到C处时，观测到小岛B的方向是北偏西，那么同时从B 观测轮船的方向是（）
A．南偏西B．东偏西C．南偏东D．南偏东
二、填空题
6. 如图，已知点D在点O的西北方向，点E在点O的北偏东50°方向，那么∠DOE
的度数为_____度．
7. 已知OC是∠AOB的平分线．有下列结论：①∠AOB=∠BOC；②∠AOC=∠AOB；
③∠AOC=∠BOC；④∠AOB=2∠AOC.其中正确结论的个数是______.
8. 一个角的补角等于这个角余角的7倍，则这个角的度数是：____.
三、解答题
9. 33°15′16″×5 .
10. 如图，已知∠AOC＝∠BOD＝90°，∠COD＝38°，求∠AOB的度数．
11. 写出图中符合下列条件的角．
(1)能用一个大写字母表示的角；
(2)以点为顶点的角；
(3)图中所有小于平角的角（可用简便方法表示）．。

华师大新版七年级上学期《4.6.1 角》同步练习卷一．填空题（共22小题）1．如图，点O是直线AB上一点，∠COD=120°，则∠AOC+∠BOD=．2．在同一平面内，∠AOB=140°，过点O作射线OC，使得∠BOC=100°，则∠AOC 的大小是度（题中的角都是小于平角的角）．3．如图，∠AOB=90°，以O为顶点的锐角共有个．4．如图所示，在已知角内画射线，画1条射线，图中共有个角；画2条射线，图中共有个角；画3条射线，图中共有个角；画n 条射线，图中共有个角．5．如图，AB是街道，点O表示一家超市，点C、D是两个居民小区，连接OC、OD，设计人员不小心把∠1、∠2、∠3的度数弄丢了，身边没有量角器，只知道∠1﹣∠2=∠2﹣∠3，则∠2的度数是．6．如图，图中共有条线段，个小于平角的角．7．如图所示，点O在直线AB上，OC为射线，∠1比∠2的3倍少20°，则∠1的度数为．8．钟表显示10点30分时，时针与分针的夹角为度．9．如图，上午6：30时，时针和分针所夹锐角的度数是．10．如图，OA的方向是北偏东15°，若∠AOC=∠AOB，则OB的方向是．11．一艘轮船行驶在B处，同时测得小岛A，C的方向分别为北偏西30°和西北方向，则∠ABC的度数是．12．如图，C岛在A岛的北偏东50°方向，从C岛看A，B两岛的视角∠ACB=105°，则C岛在B岛的北偏西方向．13．32.48°×2=度分秒．14．一副三角板按如图方式摆放，若∠α=21°37'，则∠β的度数为．15．将31.62°化成度分秒表示，结果是．16．计算77°53′26″+43°22′16″=．17．32°28′15″+15°23′48″=．18．比较大小：20.32°20°30′20″．（填“＞”、“＜”或“=”）19．计算：78°18′﹣56°46′=．20．计算：52°35′﹣32°46′=°′．21．74.16°=°′″28°7′12″=°22．比较大小：33°52′+21°54′36°27′×2（填“＞”“＜”或|=）二．解答题（共11小题）23．计算：18°13′×5﹣49°28′52″÷424．计算：（1）48°39′+67°31′﹣21°17′；（2）23°53′×3﹣107°43′÷5．25．计算：56°17′+12°45′﹣16°21′×4．26．计算：90°﹣（36°31′52″+12°22′14″）．27．计算：72°35′÷2+18°33′×4．28．计算：48°38′+67°32′﹣21°17′×5．29．计算：（1）22°18′×5；（2）90°﹣57°23′27″．30．度、分、秒的计算①56°18′+72°48′=②131°28′﹣51°32′15″=③12°30′20″×2=④12°31′21″÷3=31．计算：（1）90°﹣36°12'15″（2）32°17'53“+42°42'7″（3）25°12'35“×5；（4）53°÷6．32．读句画图填空：（1）画∠AOB；（2）作射线OC，使∠AOC=∠AOB；（3）由图可知，∠BOC=∠AOB．33．图中有多少个角？请用适当的方法把它们表示出来．华师大新版七年级上学期《4.6.1 角》同步练习卷参考答案与试题解析一．填空题（共22小题）1．如图，点O是直线AB上一点，∠COD=120°，则∠AOC+∠BOD=60°．【分析】根据平角的定义解答即可．【解答】解：∵∠AOC+∠COD+∠DOB=180°，∠COD=120°，∴∠AOC+∠BOD=180°﹣120°=60°，故答案为：60°．【点评】本题考查的是角的计算，根据平角的定义是解答此题的关键．2．在同一平面内，∠AOB=140°，过点O作射线OC，使得∠BOC=100°，则∠AOC 的大小是40或120度（题中的角都是小于平角的角）．【分析】分两种情况进行讨论：OC在∠AOB内部，OC在∠AOB外部，依据角的和差关系进行计算即可．【解答】解：如图，当OC在∠AOB内部时，∠AOC=∠AOB﹣∠BOC=140°﹣100°=40°；如图，当OC在∠AOB外部时，∠AOC=360°﹣∠AOB﹣∠BOC=120°；故答案为：40或120．【点评】本题考查了角的计算，注意要根据射线OC的位置不同，分类讨论，分别求出∠AOC的度数．3．如图，∠AOB=90°，以O为顶点的锐角共有5个．【分析】明确角的概念，依次数出以OA、OD、OC为一边的角的个数即可．【解答】解：以OA为一边的角，∠AOD，∠AOC；以OD为一边的角，∠DOC，∠DOB；以OC为一边的角，∠COB．共5个角．故答案是：5．【点评】此题考查了角的概念，首先要认识图中所示的角，再依次数出图中的角，要注意不要漏数，也不要多数．4．如图所示，在已知角内画射线，画1条射线，图中共有3个角；画2条射线，图中共有6个角；画3条射线，图中共有10个角；画n条射线，图中共有个角．【分析】根据图形数出即可得出前三个空的答案，根据结果得出规律是．【解答】解：∵在已知角内画射线，画1条射线，图中共有3个角=；画2条射线，图中共有6个角=；画3条射线，图中共有10个角=；…，∴画n条射线，图中共有个角，故答案为：3，6，10，．【点评】本题考查了对角的概念的应用，关键是能根据求出结果得出规律．5．如图，AB是街道，点O表示一家超市，点C、D是两个居民小区，连接OC、OD，设计人员不小心把∠1、∠2、∠3的度数弄丢了，身边没有量角器，只知道∠1﹣∠2=∠2﹣∠3，则∠2的度数是60°．【分析】由∠1﹣∠2=∠2﹣∠3，可得：2∠2=∠1+∠3，然后由∠1+∠2+∠3=180°，可求∠2的度数．【解答】解：∵∠1﹣∠2=∠2﹣∠3，∴∠1+∠3=2∠2，又∵∠1+∠2+∠3=180°，∴2∠2+∠2=180°，解得：∠2=60°，故答案为：60°．【点评】此题考查了角的计算，解题的关键是：利用1平角=180°解决问题．6．如图，图中共有6条线段，7个小于平角的角．【分析】根据线段的定义和角的概念写出相应的线段和角即可．【解答】解：线段有：AB、AC、BC、BD、CD、AD共6条；角有：∠B、∠ACB、∠A、∠BDC、∠ADC、∠BCD、∠ACD共7个．故答案为：6，7．【点评】本题考查了直线、射线、线段，角的定义，是基础题，熟记概念并按照一定的顺序查找是可以做的不重不漏．7．如图所示，点O在直线AB上，OC为射线，∠1比∠2的3倍少20°，则∠1的度数为130°．【分析】根据图示可得∠1+∠2=180则x+y=180，再根据∠1比∠2的3倍少20°，可得x=3y﹣20，联立两个方程可得方程组，进而解答即可．【解答】解：由图可知∠1+∠2=180°，即x+y=180，由题意知∠1比∠2的3倍少20°，即x=3y﹣20，可得：，解得：，故答案为：130°【点评】本题考查的是角的计算，关键是正确理解题意，找出题目中的等量关系，列出方程．8．钟表显示10点30分时，时针与分针的夹角为135度．【分析】计算钟面上时针与分针所成角的度数，一般先从钟面上找出某一时刻分针与时针所处的位置，确定其夹角，再根据表面上每一格30°的规律，计算出分针与时针的夹角的度数．【解答】解：∵时针在钟面上每分钟转0.5°，分针每分钟转6°，∴钟表上10点30分，时针与分针的夹角可以看成4×30°+0.5°×30=135°．故答案为：135．【点评】本题主要考查了钟面角，解题时注意：分针60分钟转一圈，每分钟转动的角度为：360°÷60=6°；时针12小时转一圈，每分钟转动的角度为：360°÷12÷60=0.5°．9．如图，上午6：30时，时针和分针所夹锐角的度数是15°．【分析】计算钟面上时针与分针所成角的度数，一般先从钟面上找出某一时刻分针与时针所处的位置，确定其夹角，再根据表面上每一格30°的规律，计算出分针与时针的夹角的度数．【解答】解：∵时针12小时转一圈，每分钟转动的角度为：360°÷12÷60=0.5°，∴时针1小时转动30°，∴6：30时，分针指向刻度6，时针和分针所夹锐角的度数是30°×=15°．故答案为：15°．【点评】本题主要考查了钟面角，解题时注意，分针60分钟转一圈，每分钟转动的角度为：360°÷60=6°；时针12小时转一圈，每分钟转动的角度为：360°÷12÷60=0.5°．10．如图，OA的方向是北偏东15°，若∠AOC=∠AOB，则OB的方向是北偏东70°．【分析】先根据角的和差得到∠AOC的度数，根据∠AOC=∠AOB得到∠AOB的度数，再根据角的和差得到OB的方向．【解答】解：∵OA的方向是北偏东15°，OC的方向是北偏西40°，∴∠AOC=15°+40°=55°，∵∠AOC=∠AOB，∴∠AOB=55°，15°+55°=70°，故OB的方向是北偏东70°．故答案为：北偏东70°．【点评】本题主要考查了方位角，方位角是表示方向的角；以正北，正南方向为基准，来描述物体所处的方向．11．一艘轮船行驶在B处，同时测得小岛A，C的方向分别为北偏西30°和西北方向，则∠ABC的度数是15°．【分析】根据方向角的定义即可得到∠ABD=30°，∠DBC=45°，再根据∠ABC=∠DBC﹣∠ABD进行计算即可．【解答】解：如图，小岛A，C的方向分别为北偏西30°和西北方向，∴∠ABD=30°，∠DBC=45°，∴∠ABC=∠DBC﹣∠ABD=45°﹣30°=15°．故答案为：15°．【点评】本题主要考查了方向角的定义，用方向角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边．12．如图，C岛在A岛的北偏东50°方向，从C岛看A，B两岛的视角∠ACB=105°，则C岛在B岛的北偏西55°方向．【分析】过C点作CD∥AE，根据方位角的概念，利用平行线的性质即可求解．【解答】解：过C点作CD∥AE，∵C岛在A岛的北偏东50°方向，∴∠EAC=50°，∴∠ACD=50°，∵∠ACB=105°，∴∠BCD=55°，∵AE∥BF，∴CD∥BF，∴∠CBE=55°，∴C岛在B岛的北偏西55°方向．故答案为：55°．【点评】本题主要考查了方位角的定义，平行线的性质，难度适中．正确理解方位角的定义是解题的关键．13．32.48°×2=64度57分36秒．【分析】进行度、分、秒的转化运算，注意以60为进制．将度的小数部分化为分，将分的小数部分化为秒．【解答】解：32.48°×2=64度57分36秒；故答案为：64；57；36．【点评】此类题是进行度、分、秒的转化运算，相对比较简单，注意以60为进制即可．14．一副三角板按如图方式摆放，若∠α=21°37'，则∠β的度数为68°23′．【分析】根据平角定义可得∠α+∠β=180°﹣90°=90°，再利用∠α=21°37'可得∠β的度数．【解答】解：∵∠1=90°，∴∠α+∠β=180°﹣90°=90°，∵∠α=21°37'，∴∠β=68°23′，故答案为：68°23′．【点评】此题主要考查了余角，度分秒的换算，如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．15．将31.62°化成度分秒表示，结果是31°37′12″．【分析】进行度、分、秒的转化运算，注意以60为进制．将度的小数部分化为分，将分的小数部分化为秒．【解答】解：∵0.62°=0.62×60′=37.2′，0.2×60″=12″，∴31.62°=31°37′12″．故答案为：31°37′12″【点评】此类题考查了进行度、分、秒的转化运算，相对比较简单，注意以60为进制即可．16．计算77°53′26″+43°22′16″=121°15′42″．【分析】把度、分、秒分别相加，最后满60进1后即可得出答案．【解答】解：77°53′26″+43°22′16″=121°15′42″．故答案为：121°15′42″．【点评】本题考查了度分秒之间的换算的应用，注意：1°=60′，1′=60″．17．32°28′15″+15°23′48″=47°52′3″．【分析】把度、分、秒分别相加，最后满60进1后即可得出答案．【解答】解：32°28′15″+15°23′48″=47°52′3″．故答案为：47°52′3″．【点评】本题考查了度分秒之间的换算的应用，注意：1°=60′，1′=60″．18．比较大小：20.32°＜20°30′20″．（填“＞”、“＜”或“=”）【分析】求出20.32°=20°19′12″，再比较即可．【解答】解：20.32°=20°19′12″＜20°30′20″，故答案为：＜．【点评】本题考查了度、分、秒之间的换算，能熟记1°=60′和1′=60″是解此题的关键．19．计算：78°18′﹣56°46′=21°32′．【分析】先化成77°78′﹣56°46′，再分别相减即可．【解答】解：78°18′﹣56°46′=77°78′﹣56°46′=21°32′，故答案为：21°32′．【点评】本题考查了度、分、秒之间的换算，能熟记1°=60′是解此题的关键．20．计算：52°35′﹣32°46′=19°49′．【分析】利用度减度，分减分计算即可．【解答】解：52°35′﹣32°46′=51°95′﹣32°46′=19°49′，故答案为：19；49．【点评】此题主要考查了度分秒的换算，关键是掌握1°=60′．21．74.16°=74°9′36″28°7′12″=28.12°【分析】度、分、秒之间是60进制，将高级单位化为低级单位时，乘以60，反之，将低级单位转化为高级单位时除以60．【解答】解：①∵0.16°=0.16×60′=9.6′，0.6′=0.6×60″=36″，∴74.16°=74°9′36″；②∵12″=0.2′，7.2′=0.12°，∴28°7′12″=28.12°；故答案为：74，9，36；28.12【点评】本题主要考查了度分秒的换算，度、分、秒是常用的角的度量单位，1度=60分，即1°=60′，1分=60秒，即1′=60″．22．比较大小：33°52′+21°54′＜36°27′×2（填“＞”“＜”或|=）【分析】根据度分秒的计算和比较解答即可．【解答】解：33°52′+21°54′=55°46′＜36°27′×2=72°54′，故答案为：＜【点评】此题主要考查了度分秒的计算，关键是掌握在进行度、分、秒的运算时也应注意借位和进位的方法．二．解答题（共11小题）23．计算：18°13′×5﹣49°28′52″÷4【分析】根据度分秒的除法，从大的单位算起，余数乘以进率化成小的单位再除，可得答案．【解答】解：原式=90°65′﹣48°88′52′′÷4=90°65′﹣12°22′13′′=78°42′47′′【点评】本题考查了度分秒的换算，从大的单位算起，余数化成下一单位再除．24．计算：（1）48°39′+67°31′﹣21°17′；（2）23°53′×3﹣107°43′÷5．【分析】（1）根据度分秒加法计算法则进行解答．（2）先进行度、分、秒的乘法计算，再从左往右依次计算．【解答】解：（1）48°39′+67°31′﹣21°17′=116°10′﹣21°17′=94°53′；（2）23°53′×3﹣107°43′÷5=71°39′﹣21°32′36″=50°6′24″．【点评】本题主要考查了度、分、秒的四则混合运算，是角度计算中的一个难点，注意以60为进制即可，难度适中．25．计算：56°17′+12°45′﹣16°21′×4．【分析】先计算出16°21′×4，然后再进行加减运算即可．【解答】解：56°17′+12°45′﹣16°21′×4=56°17′+12°45′﹣65°24′=3°38′．【点评】本题主要考查的是度分秒的换算，熟练掌握换算关系是解题的关键．26．计算：90°﹣（36°31′52″+12°22′14″）．【分析】先进行括号内的运算，再进行减法运算，即可得到计算结果．【解答】解：90°﹣（36°31′52″+12°22′14″）=90°﹣48°53′66″=90°﹣48°54′6″=89°59′60″﹣48°54′6″=41°5′54″．【点评】本题主要考查了度分秒的换算，具体换算可类比时钟上的时、分、秒来说明，在进行度、分、秒的运算时也应注意借位和进位的方法．27．计算：72°35′÷2+18°33′×4．【分析】一个度数除以一个数，则从度位开始除起，余数变为分，分的余数变为秒．两个度数相加，度与度，分与分对应相加，分的结果若满60，则转化为度．【解答】解：原式=36° 17′30″+74° 12′=110° 29′30″．【点评】此类题是进行度、分、秒的加法、减法计算，相对比较简单，注意以60为进制即可．计算乘法时，秒满60时转化为分，分满60时转化为度．28．计算：48°38′+67°32′﹣21°17′×5．【分析】根据度分秒的加减法，可得答案．【解答】解：原式=116°10′﹣106°25′=9°45′．【点评】本题考查了度分秒的换算，利用度分秒的换算是解题关键．29．计算：（1）22°18′×5；（2）90°﹣57°23′27″．【分析】（1）根据度分秒的乘法从小单位算起，可得答案；（2）根据相同单位相减，可得答案．【解答】解：（1）原式=110°90′=111°30′；（2）原式=89°59′60″﹣57°23′27″=32°36′33″．【点评】本题考查了度分秒的换算，解（1）的关键是满60向上一单为进一；解（2）的关键是相同单位相减．30．度、分、秒的计算①56°18′+72°48′=②131°28′﹣51°32′15″=③12°30′20″×2=④12°31′21″÷3=【分析】单位度、分、秒之间也是60进制，将高级单位化为低级单位时，乘以60，反之，将低级单位转化为高级单位时除以60．【解答】解：①56°18′+72°48′=129°6′；②131°28′﹣51°32′15″=79°55′45″③12°30′20″×2=25°40″；④12°31′21″÷3=4°10′27″．【点评】本题考查了度分秒的换算．相同单位相加，满60时向上一单位进1．31．计算：（1）90°﹣36°12'15″（2）32°17'53“+42°42'7″（3）25°12'35“×5；（4）53°÷6．【分析】根据度分秒的换算，可得答案．【解答】解：（1）90°﹣36°12'15″=53°47′45″；（2）32°17'53“+42°42'7″=74°59′60″=75°（3）25°12'35“×5=125°60′175″=126°2′55″；（4）53°÷6=8°50′．【点评】本题考查了度分秒的换算，利用度分秒的运算是解题关键．32．读句画图填空：（1）画∠AOB；（2）作射线OC，使∠AOC=∠AOB；（3）由图可知，∠BOC=或∠AOB．【分析】（1）利用角的定义直接画出符合题意的图形；（2）利用∠AOC=∠AOB，得出OC可能在AO的上面或下面，进而得出答案；（3）利用已知图形得出，∠BOC与∠AOB的关系．【解答】解：（1）如图：∠AOB即为所求；（2）如图：∠AOC=∠AOC′=∠AOB；射线OC，OC′为所求；（3）由图可知，∠BOC=∠AOB或∠BOC=∠AOB．故答案为：或．【点评】此题主要考查了角的概念，正确根据题意画出图形进而利用分类讨论得出是解题关键．33．图中有多少个角？请用适当的方法把它们表示出来．【分析】分别找出以点A、B、C、D为顶点的角，然后按照角的表示方法表示出来即可．【解答】解：以A为顶点的角有1个，以B为顶点的角有3个，以C为顶点的角有3个，以D为顶点的角有1个．共有8个角．它们分别是∠A，∠1，∠2，∠ABC，∠α，∠β，∠ACB，∠BDC．【点评】本题主要考查的是角的概念和表示方法，掌握角的概念和表示方法是解题的关键．。

华师大七上课课练角含答案SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#BA C4321FE D CBA 角一、选择题1．下列说法正确的是（ ）（A ） 角的两边可以度量; (B)角是由两条射线构成的图形． (C)一条直线可以看成是一个平角; (D)平角的两边可以看成直线． 2．下列说法不正确的是（ ）（A ） 两个锐角的和不一定大于直角; (B)两个钝角的和不一定大于平角． (C)只有锐角才有余角; (D)任何小于平角的角都有补角． 3．从∠AOB 的顶点O 引出两条射线OC 、OD 两条射线，图中共有角的个数为（ ）（A ）4个． （B ）5个． （C ）6个． （D ）7个． ４．下列各角中，是钝角的为（ ）（A ）周角32． （B ）周角41． （C ）平角32． （D ）平角21． ５．如图，共有（ ）个小于平角的角． （A ）5． （B ）6． （C ）7． （D ）8．第5题图6．用一副三角板的内角可以画出大于0o 且小于180o 的不同角度的角共有（ ）（A ）9种． （B ）10种． （C ）11种． （D ）12种． 7．如图，已知∠1=∠2，∠3=∠4，则下列结论正确的个数为（ ） ①AD 平分∠BAF ． ②AF 平分∠DAC ．③AE 平分∠DAF ． ④AE 平分∠BAC ．（A ）1． （B ）2． （C ）3． （D ）4． 8．∠A 与∠B 互补，∠B 与∠C 互余，则∠A 一定是（ ）（A ）锐角． （B ）钝角． （C ）直角． （D ）不能确定． 9．八点三十分，这一时刻，时针与分针夹角是（ ）（A ）70°． （B ）75°． （C ）80°． （D ）85°． 二、填空题10．角是由有 的两条射线组成的图形，两条射线的 是这个角的顶点，角也可以看成是由一条射线 ． 11．1个周角= 个平角= 个直角．12．当时钟的时间为6:30分时,时针与分针的夹角为 度．13．从8点10分到8点40分,时钟的时针转过 度,时钟的分针转过度．14．108°42ˊ= 度；°= 度 分 秒. 15．13°39ˊ+64°45ˊ= ．16．图中共有 角,以点A 为顶点的角是 .（第7题图）南东西北BAO E D C B AB(第16题图) (第17题图)17．如图,已知∠COE =∠BOD =∠AOC =90°,则图中互余的角有 对,互补的角有 对.18．如图,A ,B ,C 分别代表学校、图书馆、小红家，学校和图书馆分别在小红家的北偏西方向，学校又在图书馆的北偏东方向，那么图中点A 表示 ，点B 表示 ，点C 表示 .（第18题图） (第20题图)19．如果车站在学校的北偏东10千米处,那么学校在车站的 方向处．20．如图,∠BOC =60°,OE 、OD 分别为∠AOC 和∠BOC 的平分线,则∠EOD = ,∠COE = ,∠BOE 的平分线是 ． 三、解答题 21．计算：①51325536'︒+'︒ ②35262⨯'︒③33370268'︒-'︒ ④370÷︒22．如图,以B23．如果在∠AOD 的内部从顶点O 引出2条射线,求图中有多少个角如果引出3条射线呢如果引出100条射线呢你发现了什么规律ODC B A24．已知一个角的补角比这个角的余角的三倍还多20°,求这个角．25．在图中画出:(1)表示北偏东30°的射线OA；(2)表示东南方向的射线OB；(3)表示南偏西方向60°的射线OC．26．如图，∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11.求∠AOB与∠BOC的度数.D CBO A27．在平面上,∠AOB=100°,∠BOC=60°,若OM平分∠AOB,ON平分∠BOC,求∠MON的度数．28．小刚星期天早晨8:00出发去奶奶家,中午11:30返回.他出发时和返回时时钟的时针和分针夹角各是多少时针转过的角度是多少答案:一、二、10.公共端点 公共端点 绕端点旋转而得到的图形 4° ° 180° 846135'''︒°24ˊ 16. 8 ∠A 17. 4,5 18.学校 图书馆 小红家 19.南偏西 10千米 ° 60° 射线OC三、21.①69°10ˊ②187°15ˊ③30°47ˊ ④23°20ˊ个 ∠ABE ∠ABC ∠EBC 4个 ∠ADE ∠ADB ∠BDC ∠CDE 个 10个 5151 ° 25.略26. 20°, 70° 27. 80°或 20° ° 165° 105°课题： 角 讲学槁学习目标：1、认识互为余角和补角概念，理解互为余角和补角主要反映角的数量关系。

4321E D CBA角的练习题一、选择题1．下列说法正确的是（ ）角的两边可以度量; (B)角是由两条射线构成的图形． (C)一条直线可以看成是一个平角; (D)平角的两边可以看成直线． 2．下列说法不正确的是（ ）两个锐角的和不一定大于直角; (B)两个钝角的和不一定大于平角． (C)只有锐角才有余角; (D)任何小于平角的角都有补角．3．从∠AOB 的顶点O 引出两条射线OC 、OD 两条射线，图中共有角的个数为（ ） （A ）4个． （B ）5个． （C ）6个． （D ）7个． ４．下列各角中，是钝角的为（ ）（A ）周角32． （B ）周角41． （C ）平角32． （D ）平角21．５．如图，共有（ ）个小于平角的角．（A ）5． （B ）6． （C ）7． （D ）8．（第5题图） 6．用一副三角板的内角可以画出大于0º且小于180º的不同角度的角共有（ ） （A ）9种． （B ）10种． （C ）11种． （D ）12种． 7．如图，已知∠1=∠2，∠3=∠4，则下列结论正确的个数为（ ） ①AD 平分∠BAF ． ②AF 平分∠DAC ．③AE 平分∠DAF ． ④AE 平分∠BAC ．（A ）1． （B ）2． （C ）3． （D ）4． 8．∠A 与∠B 互补，∠B 与∠C 互余，则∠A 一定是（ ）（A ）锐角． （B ）钝角． （C ）直角． （D ）不能确定． 9．八点三十分，这一时刻，时针与分针夹角是（ ） （A ）70°． （B ）75°． （C ）80°． （D ）85°． 二、填空题（第7题图）DC BAODCBA南东西北BAEDCBA10．角是由有 的两条射线组成的图形，两条射线的 是这个角的顶点，角也可以看成是由一条射线 ． 11．1个周角= 个平角= 个直角．12．当时钟的时间为6:30分时,时针与分针的夹角为 度．13．从8点10分到8点40分,时钟的时针转过 度,时钟的分针转过 度． 14．108°42ˊ= 度；35.28°= 度 分 秒. 15．13°39ˊ+64°45ˊ= ．16．图中共有 角,以点A 为顶点的角是 .B(第16题图)(第17题图)17．如图,已知∠COE=∠BOD=∠AOC=90°,则图中互余的角有 对,互补的角有 对. 18．如图,A,B,C 分别代表学校、图书馆、小红家，学校和图书馆分别在小红家的北偏西方向，学校又在图书馆的北偏东方向，那么图中点A 表示 ，点B 表示 ，点C 表示 .（第18题图） (第20题图)19．如果车站在学校的北偏东10千米处,那么学校在车站的 方向 处． 20．如图,∠BOC=60°,OE 、OD 分别为∠AOC 和∠BOC 的平分线,则∠EOD= , ∠COE= ,∠BOE 的平分线是 ． 三、解答题 21．计算：①51325536'︒+'︒ ②35262⨯'︒③33370268'︒-'︒ ④370÷︒22．如图,以B 为顶点的角共有几个?请把它们写出来,以D23．如果在∠AOD 的内部从顶点O 引出2条射线,求图中有多少个角?如果引出3条射线呢?如果引出100条射线呢?你发现了什么规律?ODC B A24．已知一个角的补角比这个角的余角的三倍还多20°,求这个角．25．在图中画出:(1)表示北偏东30°的射线OA ； (2)表示东南方向的射线OB ； (3)表示南偏西方向60°的射线OC ．26．如图，∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11.求∠AOB与∠BOC的度数.D CBO A27．在平面上,∠AOB=100°,∠BOC=60°,若OM平分∠AOB,ON平分∠BOC,求∠MON的度数．28．小刚星期天早晨8:00出发去奶奶家,中午11:30返回.他出发时和返回时时钟的时针和分针夹角各是多少?时针转过的角度是多少?角的练习题一．判断：1.若∠1+∠2+∠3=180°, 则∠1,∠2,∠3互补。