当前位置：文档之家 › 三垂线定理及其典型例题 ppt

三垂线定理及其典型例题 ppt

  • 格式：ppt
  • 大小：223.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

三垂线定理及其应用PPT优选课件

三垂线定理及其应用PPT优选课件

2020/10/18
8
练习:
1. 如图,PA垂直⊙O所在平面,AB为圆的直径,C 为 圆上的 任意一点(不同于A,B),则图中有多少个直角三角形?
P
答:有4个,分别是: △PAB,△PAC,△ACB,△PCB. A
•O B C
2020/10/18
9
定理应用
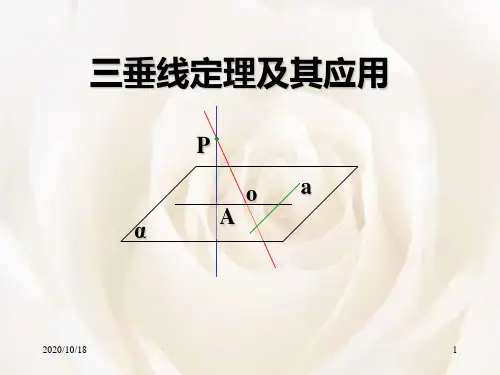
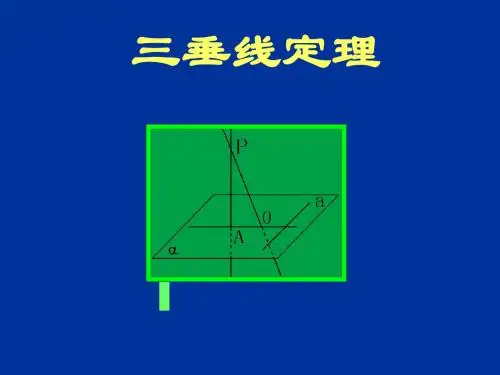
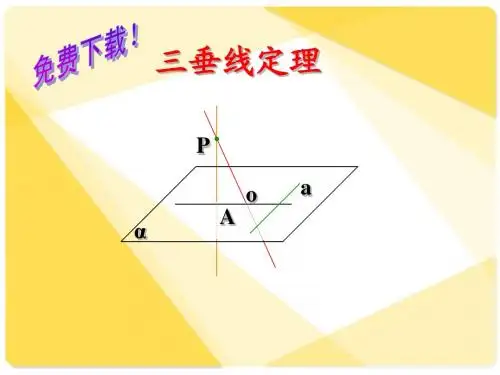
三垂线定理
例3,道路旁有一条河，彼岸有电塔AB，高15m，只有测角
可测得C、D的距离等于a米, ∴BC= a米，
在直角△ABC中, AC2=AB2+BC2， AC= 152+a2 米
答：电塔顶A与道路的距离是 152a2米。
A
B
2020/10/18
90°
C
45是异面直线a,b的公垂线段,AB=2, a,b成30o角,在a上取点P使AP=4,则点P到直
感谢阅读！为了方便学习和使用，本文档的内容可以在下载后随意修改，调整和打印。欢迎下载！
汇报人：XXX 日期：20XX年XX月XX日
线b的距离:2___2_.
A
P• a
B
C
Db
2020/10/18
12
定理应用
例4.如图,长方体 ABCD-A1B1C1D1中,AB=AD=2 2 ,
AA1= 3, E,F分别为AB和AD的中点,求平面A1EF
和平面ABCD所成二面角的大小?
解: 连接BD,AC,AC交EF于G, 连接A1G
D
1
C1
证明：连结BD， 连结A1B
D1
∵DD1⊥平面ABCD
A1
∴BD是斜线D1B在平面ABCD上的射影
∵ABCD是正方形∴AC⊥BD
C1 B1
(AC垂直射影BD)，∴AC⊥BD1

人教版高中数学课件 第二册：三垂线定理

人教版高中数学课件 第二册：三垂线定理

P
D1
C1
A1
D A C
B1 D
C
M (2) B
A (3)
(1)
B
三垂线定理解题的关键：找三垂！
解 题 回 顾
怎么找？
一找直线和平面垂直 二找平面的斜线在平面 内的射影和平面内的 一条直线垂直 P
α
A
O
a
注意：由一垂、二垂直接得出第三垂 并不是三垂都作为已知条件
使用三垂线定理还应注意些什么？
解 题 回 顾
α
P
A
O
a
？
α
P A
线斜垂直
O
a
平面内的一条直线和 平面的一条斜线在平 面内的射影垂直
平面内的一条直 线和平面的一条 斜线垂直
三垂线定理的逆定理
在平面内的一条直线，如果和这个平面的一 条斜线垂直，那么，它也和这条斜线的射影垂直。 P 已知：PA，PO分 别是平面 的垂线和斜 线，AO是PO在平面 A O
线斜垂直
例3 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC， PO⊥ ，垂足分别是E、F、O，PE=PF P 求证：∠BAO=∠CAO 分析： 要证 ∠BAO=∠CAO E B 只须证OE=OF, OE⊥AB,OF⊥AC O
O
a
A AO⊥a
a⊥平面PAO
PO平面PAO
a⊥PO
三垂线定理：
在平面 内的一条直线，如果和这个平 面的一条斜线的射影垂直，那 么，它就和这条斜线垂直。
P
O
a
A
PA⊥ a
PA ⊥a
AO⊥a

三垂线定理及其典型例题知识讲解

三垂线定理及其典型例题知识讲解

P a
Ao α
用法：
∵PA⊥α， a α，
AO是斜线PO在平面 α内的射影， a⊥PO ∴ a⊥AO
说明：三垂线定理及其逆定理是证明线线垂
直的重要方法。
例题分析： 1、判定下列命题是否正确
三垂线定理
(1)若a是平面α的斜线、直线b垂直于a在平面
α内的射影，则a⊥b。
( ×)
(2)若a是平面α的斜线，b是平面α内的直线，
二、平面的斜线、垂线、射影
三垂线定理
PO是平面α的斜线, O为斜足; PA是平面α的垂线, A为垂足; P AO是PO在平面α内的射影.
oa
如果a α, a⊥AO，
α
A
思考a与PO的位置关
系如何？
结论：a⊥PO 为什么呢？
二、三垂线定理：
三垂线定理
在平面内的一条直线，如果和这个平面的一条
斜线的射影垂直，那么它也和这条斜线垂直。
D1
C1
又DD1⊥平面ABCD
A1
B1
∴BD是斜线D1B在平面ABCD上的
射影
∵AC在平面AC内，∴BD1⊥AC
D
请同学思考：如何证明D1B⊥AB1 A 而AB1， AC相交于点A且都在平面
AB1C内 ∴BD1⊥平面AB1C
C B
三垂线定理
关于三垂线定的应用，关键是找出平面(基准面)的垂线。 至于射影则是由垂足、斜足来确定的，因而是第二位的。
三垂线定理及其典型例题
一、射影的概念
定义：自一点P向平面α引垂线，垂足P1 叫做P
在平面α内的正射影（简称射影）。 如果图形F上的所有点在一平面内的射影构成图 形F1，则F1叫做图形F在这个平面内的射影。
.P

三垂线定理及其典型例题ppt课件

三垂线定理及其典型例题ppt课件

思考：
a 如果把定理中的条a⊥AO与结 论a⊥PO互换，命题是否成立？
三垂线定理的逆定理： 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
在平面内的一条直线，如果它和这个平面的一条 斜线垂直，那么它也和这条斜线在这个平面内的 射影垂直。
三垂线定理
(1)若a是平面α的斜线、直线b垂直于a在平面
α内的射影，则a⊥b。
( ×)
(2)若a是平面α的斜线，b是平面α内的直线，
且b垂直于a在β内的射影，则a⊥b。
( ×)
强调：1°四线是相对同一个平面而言
2°定理的关键找“平面”这个参照学。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
P a
Ao α
用法：
∵PA⊥α， a α，
AO是斜线PO在平面 α内的射影， a⊥PO ∴ a⊥AO
说明：三垂线定理及其逆定理是证明线线垂
直的重要方法。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例题分析： 1、判定下列命题是否正确
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
复习提问：
1。直线与平面垂直的定义。 2。直线与平面垂直的判定定理。 3。证明线面垂直的方法。 4。证明线线垂直的方法。
一、射影的概念 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能

三垂线定理说课ppt

三垂线定理说课ppt

证明：连结AO，并延长AO交 BC于D ∵O是△ABC的垂心
P
∴AD ⊥BC
又∵ AＤ是PA在平面ABC 的射影
A
O
C D B∴ PA ⊥ BC五、课堂小结：知识内容：三垂线定理
应用步骤： “一垂二射三证” 思想方法：转化思想，点明转化的关键是
“找平面的垂线”。
六、布置作业：
1、已知：如图, VA⊥VB, VA⊥VC , VD⊥BC. 求证： AD⊥BC V
PO平面PAO
a⊥PO
三、新授
三垂线定理
在平面内的一条直线，如果和这个平面的一条
斜线的射影垂直，那么它也和这条斜线垂直。
(线射垂直 线斜垂直) P a
A

O
三垂线定理包含几种垂直关系？
①线面垂直 ②线射垂直 ③ 线斜垂直
P A O P P O
α
a
α
A
a
α
A
O
a
直 线 和
平面垂直
平面内的直线 和平面一条斜 线的射影垂直
B
A
D
C
2、如图，AB是⊙O的直径，PA垂直圆O所在的 平面，点C是圆周上异于A、B的一点。 试说明： ①图中有哪几个直角三角形？ ②如果点C在圆周上运动呢？
P
A
C
·
O
B
(3)非书面作业：
① 、三垂线定理的逆命题是否成立？
② 、证明空间两条直线垂直有哪几种途径？
谢 谢 大 家！
精品课件！
精品课件！
2、 已知：PA⊥平面PBC，PB=PC， P M是BC的中点， 求证：BC⊥AM C 证明: PB=PC
M是BC的中点
A
M B BC⊥AM

高二数学下学期-三垂线定理课件人教.ppt

高二数学下学期-三垂线定理课件人教.ppt
这是偶然的巧合，还是必然？
cos·cos=cos
A
=∠AOB
=∠DOB
=∠AOD
O
BM
ED
P
A
Oa
AE⊥OD
PO⊥ a
三垂线定理
在平面内的一条直线，如果和这个平面的一条 斜线的射影垂直，那么它就和这条斜线垂直。
如图：已知 PA、PO
P
分别是平面的垂线、斜
线，AO是PO在平面上
的射影。a ，a⊥AO。
不在平面内，定理 就不一定成立。
Oa
αA
练习：
判断下列命题是否正确：
⑴若a是平面α的斜线，直线b垂直于
a在平面α内的射影，则 a⊥b （ ×）
ห้องสมุดไป่ตู้
⑵若 a是平面α的斜线，平面β内
的直线b垂直于a在平面α内的射
影，则 a⊥b
（× ）
⑶若a是平面α的斜线，直线b α
且b垂直于a在另一平面β内的射
影则a⊥b
α
α
α
直线和 平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
例1 已知P 是平面ABC 外一点， PA⊥平面 ABC ，AC ⊥ BC， 求证： PC ⊥ BC
证明：∵ P 是平面ABC 外一点
P
PA⊥平面ABC
∴PC是平面ABC的斜线
∴AC是PC在平面ABC上的射影
（
×
）
⑷若a是平面α的斜线,b∥α,直线
b垂直于a在平面α内的射影，
则 a⊥b
（）
⑷若a是平面α的斜线,b∥α,直线 b垂直 于a在平面α内的射影，则 a⊥b
l P
A Oa α

三垂线定理 ppt(沪教版高三上)

⑵ 由⑴知BD ⊥面AA1C A1C在面AA1C ∴BD⊥A1C
A1
D A
C1 B1
C B
D1
A1
4、在正方体AC1中，AC1在平
面ABCD、BB1C1C内的射
影分别（ AC、B1C ）
D
A 平面 ABCD、BB1C1C 内 的 直线BD、BC1分别 与 对应的斜线是否垂直？与 对应的射影呢？ 垂直
C1 B1
C F B
小结
三垂线定理：
在平面内的一条直线、如果它和这个平面 的一条斜线的射影垂直，⊥那么它也和这条 斜线垂直。
练习和作业
D1
பைடு நூலகம்
1、已知：O为正方体AC1的底面ABCD 的中点。求证：D1O⊥EF
A1
E
C1 F
B1
2、已知P为△ABC所在平面外一点，
若P在平面ABC 内的射影是△ABC的垂
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证：⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
A1
求证：C1E⊥DF
证明：正方形ABCD 中，E、F
D
分别为AB、BC中点，
∴△DCF≌△CBE.
A
E
∠CDF＝ ∠BCE 又∠CDF＋
∠DFC＝900
∴ ∠BCE＋ ∠DFC＝900
∴ DF⊥CE 又因为CC1 ⊥平ABCD ∴C1E在平面ABCD 内的射影为CE。 由三垂线定理知 C1E ⊥DF

三垂线定理 PPT课件 6 人教课标版


•
80、乐观者在灾祸中看到机会；悲观者在机会中看到灾祸。
三垂线定理的逆理：
在平面内的一条直线，如果和 这个平面的一条斜线垂直，那 么，它也和这条斜线的射影垂 直。
线射垂直
定 理
逆 定 理
线斜垂直
例3 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC，
PO⊥ ，垂足分别是E、F、O，PE=PF
•
36、每临大事，心必静心，静则神明，豁然冰释。
•
37、别人认识你是你的面容和躯体，人们定义你是你的头脑和心灵。
•
38、当一个人真正觉悟的一刻，他放弃追寻外在世界的财富，而开始追寻他内心世界的真正财富。
•
39、人的价值，在遭受诱惑的一瞬间被决定。
•
40、事虽微，不为不成；道虽迩，不行不至。
•
41、好好扮演自己的角色，做自己该做的事。
题 直线垂直的判定定理， 回 这两条直线可以是：
顾 ①相交直线
②异面直线
e dc
αA
Ob a
注意：如果将定理中 例如：当 b⊥ 时，
“在平面内”的条件
b⊥OA
解 去掉，结论仍然成立 吗？
但 b不垂直于OP
题
P
b
回 顾
直线a 在一定要在 平面内，如果 a 不
在平面内，定理就 不一定成立。
•
42、自信人生二百年，会当水击三千里。
•
43、要纠正别人之前，先反省自己有没有犯错。
•
44、仁慈是一种聋子能听到、哑巴能了解的语言。
•
45、不可能！只存在于蠢人的字典里。

0039数学课件：三垂线定理(不错)


C H
B E
4×6 12 在Rt△PBC中，PE= ------ = ---42+62 13 144 2 29 在Rt△APE中，AE= PA2+PE2= 9+ --- = ---13 13
三垂线定理
例4、道旁有一条河，彼岸有电塔AB，高15m，只有测角
器和皮尺作测量工具，能否求出电塔顶与道路的距离？ 解：在道边取一点C， 使BC与道边所成水平角等于90°， 再在道边取一点D， 使水平角CDB等于45°， 测得C、D的距离等于20cm A
A A1 D1 B1 C1
D
B
C
三垂线定理
关于三垂线定理的应用，关键是找出平面(基准面)的垂 线。至于射影则是由垂足、斜足来确定的，因而是第二位的。 从三垂线定理的证明得到证明a⊥b的一个程序：一垂、 二射、三证。即 第一、找平面(基准面)及平面垂线
P
a α A o
第二、找射影线，这时a、b便成平面上
三垂线定理
P o α A
a
复习： 什么叫平面的斜线、垂线、射影？
三垂线定理
PO是平面α的斜线,
O为斜足; PA是平面α
P o
α A a
的垂线, A为垂足; AO 是PO在平面α内的射 影. 如果a α, a⊥AO， 思考a与PO的位置关 系如何？
学生答：a⊥PO
为什么呢？
三垂线定理
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
90°
C
45°
D
三垂线定理
小
结
三垂线定理：在平面内的一条直线，如果 和这个平面的一条斜线的射影垂直，那么它也 和这条斜线垂直。 1°定理中四条线均针对 同一平面而言

三垂线定理3 PPT课件


P
EBO A
C
F
已知H是ABC的垂心，PH 平面ABC， 连AH交BC于D，求证：PH BC
P
A H
C D
B
在立体图形V ABC中，VO 平面ABC，O CD VA VB，AD BD。求证：CD AB。
V

C
O D
B
习题9.4
1.怎样判断线面垂直?线面垂直有哪 些性质?
已知正方形ABCD的边长是a，PA 平面AC, PA a 求：（1）AD到平面PBC的距离 （2）PC与平面AC所成的角
P
P
A D
B
A
C
D
B C
(思考)平面的斜线不能与这个平面内的 所有直线都垂直,那么它能否与这个平 面内的某些直线垂直?
p
o
a
A
（1）定理： PO , PA A, a
a OA
a PA
（2）逆定理： PO , PA A, a
a PA
a OA
P
A
三垂线定理基本图形的特点分析
1:一面
O
a
2:四线
3:三垂直
线面垂直
线射垂直
P
线斜垂直
a
A O
1.求证:如果一个角所在平面外一点到角 两边距离相等,那么这一点在平面内射影 在这个角的平分线所在直线上.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

PA2+PE2=
-
9+
-11-43-4
=
-21-3-2-9
15
系如何？
-
4
结论：a⊥PO 为什么呢？
二、三垂线定理：
三垂线定理
在平面内的一条直线，如果和这个平面的一条
斜线的射影垂直，那么它也和这条斜线垂直。
PA⊥α ①
aα
PA⊥a
AO⊥a
② a⊥平面PAO
PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
② 线线垂直
③ 线面垂直
线线垂直
性质定理
判定定理
性质定理
求证：∠BAO=∠CAO
证明：连接PA，OE，OF∵ PE⊥AB，PF⊥AC，PO⊥ α，
∴AB⊥OE，AC⊥OF（三垂线定理的逆定理）
∵ PE=PF，PA=PA，∴Rt PAE≌RtPAF。
∴AE=AF又AO=AO∴，∴Rt AOE≌Rt AOF。
∴ ∠BAO=∠CAO
-
11
三垂线定理
例4、道旁有一条河，彼岸有电塔AB，高15m，只有测角 器和皮尺作测量工具，能否求出电塔顶与道路的距离？ 解：在道边取一点C，使BC与道边所成水平角等于90°，
再在道边取一点D，使水平角CDB等于45°， 测得C、D的距离等于20cm
A
B
90°
C
45°
D
-
12
∵BC是AC的射影 且CD⊥BC ∴CD⊥AC
三垂线定理
因此斜线AC的长度就是电塔顶与道路的距离。
∵∠CDB=45°，CD⊥BC，CD=20cm ∴BC=20m， 在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm) 答：电塔顶与道路的距离是25m。
思考：
a 如果把定理中的条a⊥AO与结
论a⊥PO互换，命题是否成立？
-
6
三垂线定理的逆定理：
在平面内的一条直线，如果它和这个平面的一条 斜线垂直，那么它也和这条斜线在这个平面内的 射影垂直。
P a
Ao α
用法：
∵PA⊥α， a α，
AO是斜线PO在平面 α内的射影， a⊥PO ∴ a⊥AO
说明：三垂线定理及其逆定理是证明线线垂
A
B
90°
C
45°
D
-
13
小结
三垂线定理
三垂线定理：在平面内的一条直线，如果 和这个平面的一条斜线的射影垂直，那么它也 和这条斜线垂直。
1°定理中四条线均针对同一平面而言 2°应用定理关键是找“基准面”这个参照系 3°操作程序分三个步骤——“一垂二射三证”
-
14
三垂线定理
例4、设PA、PB、PC两两互相垂直，且PA=3，PB=4，
D
C
请同学思考：如何证明D1B⊥AB1 A 而AB1， AC相交于点A且都在平面
AB1C内 ∴BD1⊥平面AB1C -
B
9
三垂线定理
关于三垂线定的应用，关键是找出平面(基准面)的垂线。 至于射影则是由垂足、斜足来确定的，因而是第二位的。
从三垂线定理的证明得到证明a⊥b的一个程序：一垂、 二射、三证。即
PC=6，求点P到平面ABC的距离。
解: 作PH⊥平面ABC， P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内的射影 A
H
C E
∴BC⊥AH
B
在Rt△PBC中，PE= -4-×--6-- = -1-2--
42+62
13
在Rt△APE中，AE=
-
8
三垂线定理
2、如图，已知正方体ABCD-A1B1C1D1中，连结BD1， AC，CB1，B1A，求证：BD1⊥平面AB1C
证明：连结BD，连结A1B ∵ABCD是正方形，∴AC⊥BD
D1
C1
又DD1⊥平面ABCD
A1
B1
∴BD是斜线D1B在平面ABCD上的
射影
∵AC在平面AC内，∴BD1⊥AC
第一、找平面(基准面)及平面垂线 第二、找射影线，这时a、b便成平面上的一条直线与 一条斜线。 第三、证明射影线与直线a垂直，从而得出a与b垂直。
-
10
例3.如果一个角所在平面外一点到角的两边的距离相
等，那么这点在平面内的射影在这个角的平分线上。
A
αF
P
B E
O C
已知：∠BAC在平面α内，点在α外， PE⊥AB，PF⊥AC，PO⊥ α，垂足 分别是E、F、O，PE=PF
直的重要方法。
-
7
例题分析： 1、判定下列命题是否正确
三垂线定理
(1)若a是平面α的斜线、直线b垂直于a在平面
α是平面α的斜线，b是平面α内的直线，
且b垂直于a在β内的射影，则a⊥b。
( ×)
强调：1°四线是相对同一个平面而言
2°定理的关键找“平面”这个参照学。
三垂线定理
P
oa
α
A
-
1
复习提问：
1。直线与平面垂直的定义。 2。直线与平面垂直的判定定理。 3。证明线面垂直的方法。 4。证明线线垂直的方法。
-
2
一、射影的概念
定义：自一点P向平面α引垂线，垂足P1 叫做P
在平面α内的正射影（简称射影）。
如果图形F上的所有点在一平面内的射影构成图
形F1，则F1叫做图形F在这个平面内的射影。
-
5
对三垂线定理的说明：
三垂线定理
1、三垂线定理描述的是PO(斜线)、AO(射影)、
a(直线)之间的垂直关系。
2、a与PO可以相交，也可以异面。
3、三垂线定理的实质是平面的一条斜线和
平面内的一条直线垂直的判定定理。
用法：∵PA⊥α， a α，AO是斜线PO在平面α
内的射影，a⊥AO ∴a⊥PO
P Ao α
.P
α
p1
思考：
1。两条异面直线在同一平面 内的射影的位置关系如何？
2。一个三角形在另一平面 中的射影可能是什么图形？
-
3
二、平面的斜线、垂线、射影
三垂线定理
PO是平面α的斜线, O为斜足; PA是平面α的垂线, A为垂足; AO是PO在平面α内的射影.
P
oa
如果a α, a⊥AO，
α
A
思考a与PO的位置关