三垂线定理

格式：ppt
大小：447.50 KB
文档页数：24

下载文档原格式

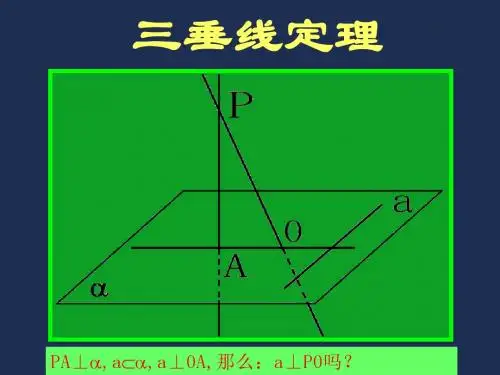
三垂线定理及其逆定理

三垂线定理及其逆定理知识点：1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用；教学过程：1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：PA, PO分别是平面的垂线和斜线，AO是PO在平面的射影, a, a⊥AO。

求证：a⊥PO；证明：说明：（1）线射垂直（平面问题）线斜垂直（空间问题）；2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；3）三垂线定理描述的是 PO（斜线）、AO（射影）、a（直线）之间的垂直关系。

4）直线a与PO可以相交，也可以异面。

5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

例 1.已知P是平面ABC外一点，PA⊥ABC, AC⊥BC。

求证：PC⊥BC。

例2.已知PA⊥正方形ABCD所在平面，O为对角线BD的中点。

求证：PO⊥BD,PC⊥BD。

C例4.在正方体AC中，求证：AC⊥B D , AC⊥BC；2．写出三垂线定理的逆命题，并证明它的正确性；命题：已知：求证：证明：说明：例 2 ．在空间四边形 ABCD 中，设AB⊥CD, AC⊥BD。

求证：（1）AD⊥BC；（2）点 A在底面 BCD上的射影是BCD的垂心；例 3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上已知：求证：说明：可以作为定理来用。

例5．已知：Rt ABC中，A=,AB=3,AC = 4 ，PA是面ABC的斜线，PAB = PAc = 。

23 (1)求 PA 与面 ABC 所成的角的大小;(2)当 PA的长度等于多少的时候，点 P在平面 ABC内的射影恰好落在边 BC上；B作业：1.正方体ABCD - A1B1C1D1 , E, F分别是A1A, AB上的点, EC1 ⊥EF.求证: EF⊥EB。

2.已知：PA⊥平面PBC，PB = PC, M是BC的中点。

三垂线定理

1. 在正方体AC1中,E,G分别是AA1和是所 1 P CC1的中点, F在AB上,且C1E⊥EF, PD 成 AB 则EF与GD所成的角的大小为( D ) 边的上 (A) 30° (B) 45° (C) 60°(D) 90° 角的 D1 是一 C1 EB1是EC1在平面AB1 EC AB 多点内的射影 A1 少求 B1 G ? 异 EB1 ⊥EF E D 面 M C DG‖AM‖EB1 直 EF ⊥DG A 线 B F B1C
F D O B E
C
思考题:在四面体ABCD中,已知 ⊥CD, 思考题:在四面体中已知AB⊥ , AC⊥BD,求证:AD⊥BC 求证: ⊥ ⊥ 求证证明: 于点O, 证明:作AO⊥平面 ⊥平面BCD于点 , 于点连接BO, , 连接 ,CO,DO,则BO, , , A CO,DO分别为 ,AC, 分别为AB, , , 分别为 AD在平面在平面BCD上的射影. 上的射影. 在平面上的射影 ∵AB⊥CD,∴BO⊥CD, ⊥ , ⊥ , 同理CO⊥BD, ⊥ , 同理的垂心, 于是O是于是是△BCD的垂心, 的垂心 ∴DO⊥BC,于是 ⊥BC. ⊥ ,于是AD⊥ B O C D
例2 如果一个角所在平面外一点到角的两边距离相等, 的两边距离相等,那么这一点在平面上的射影在这个角的平分线上. 上的射影在这个角的平分线上.
四,两个重要结论
练.(1)已知四面体 ( )已知四面体P-ABC, PA,PB,PC两两垂直,求证: 两两垂直, , , 两两垂直求证: P在平面在平面ABC内的射影是在平面内的射影是 A △ABC的垂心. 的垂心. 高的交点) (高的交点)
五,知识方法总结
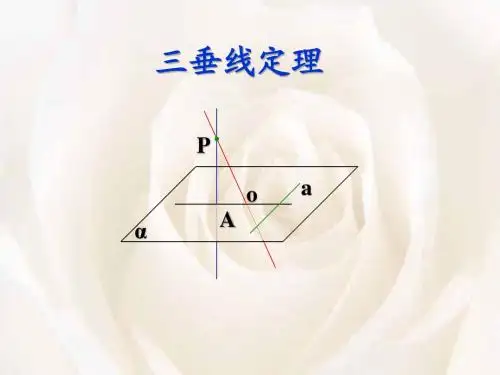
1,三垂线定理及逆定理. 三垂线定理及逆定理. 作用:用于证明线线垂直. 2,作用:用于证明线线垂直. 用法:先找线面垂直, 用法:先找线面垂直,再找线射垂直,从而推出线斜( (斜)垂直,从而推出线斜(射) 垂直. 垂直.平面可能水平放置也可能竖直或倾斜放置. 直或倾斜放置. 3,两个射影结论. 两个射影结论.

三垂线定理

例2、如图，已知正方体ABCD-A1B1C1D1中，连结BD1， AC，CB1，B1A，求证：BD1⊥平面AB1C
D1 A1 B1
C1
D
A B
C
例2、如图，已知正方体ABCD-A1B1C1D1中，连结BD1， AC，CB1，B1A，求证：BD1⊥平面AB1C
D1 A1 B1
C1
D
A B
C
三垂线定理
平面的一条斜线的射影垂直，那么它也和这条斜线垂直。线射垂直线斜垂直
三垂线逆定理：线斜垂直
在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直。
线射垂直
P
a α
A o
三垂线定理
例题分析：
1、判定下列命题是否正确 (1)若b是平面α 的斜线、直线a垂直于b在平面 α 内的射影，则b⊥a。 ( ×)
P a α A
①
o
② ③
线线垂直线线垂直线面垂直线面垂直线面垂直定判定定理线面垂直定义义
①
三垂线定理
三垂线定理：在平面内的一条直线，如果和这个
平面的一条斜线的射影垂直，那么它也和这条斜线垂直。已知: PA、PO分别是平面α的垂线、斜线，AO 是PO在平面α内的射影，且a α，a⊥AO求证： a⊥PO
α A o
①
a⊥AO AO a平面PAO
③
三垂线逆定理：
在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直。
已知: PA、PO分别是平面α的垂线、斜线，AO 是PO在平面α内的射影，且a α，a⊥PO求证： a⊥AO
线斜垂直
线射垂直
P
a α A o

三垂线定理

证明：∵H是∆ABC的垂心，连结AH延长交 BC于D，连结BH延长交AC于E，∴AD⊥BC， BE⊥AC，∵AP⊥平面PBC，∴BC⊥PD， AD∩PD=D，∴BC⊥平面ADP，∴BC⊥PH，又AP⊥面PBC，∴AP⊥PB，由已知BP⊥PC， ∴PB⊥面APC，又BE⊥AC，∴PE⊥AC， ∴AC⊥面PBE，∴PH⊥AC，AC∩BC=C， ∴PH⊥面ABC，∴H是P点在平面ABC的射影。
1.直接利用三垂线定理证明下列各题：
(1) PA⊥正方形ABCD所在平面，O为对角线BD的中点求证：PO⊥BD，PC⊥BD (2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点，求证：BC⊥AM
(3) 在正方体AC1中，求证：A1C⊥B1D1，A1C⊥BC1
P
P
D1
C1
A
D
O
A
B
C
(1)
∴ ∠AFC= ∠MDF ， ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°，
∴ DM ⊥AF，又ABC-DEF为直三棱柱，∴ CF⊥EF，又EF⊥DF，∴ EF⊥平面AF，由三垂线定理知AE⊥DM
能力拓展：
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC，求证： ∆ABC的垂心H是P点在平面ABC内的射影。
3. 如果一个角所在平面外一点到角的两边距离相等那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC，
PO⊥ ，垂足分别是E、F、O，PE=PF
求证：∠BAO=∠CAO
P
分析：要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥AC
?
?
?
A

【数学课件】三垂线定理

E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底部的距离为8米，求旗杆顶部A到楼底部的距离。
证明：∵AC面，a 面
∴ACa
一、三垂线定理
1.三垂线定理：在平面内的一条直线，如果和这个平面的一条 A 斜线的射影垂直，那么它也和这条斜线垂直。
已知：AC和AB分别是平面的垂
线和斜线，BC是AB在平面
C
B
a
上的射影，a，aBC。求证： aAB。
证明：∵AC面，a 面
∴ACa
∵BCa ，AC∩BC＝C
9.4 直线与平面垂直的判定和性质
————————————————————— —
§6 三垂线定理
教学目的
• 掌握三垂线定理及逆定理 • 运用三垂线定理及逆定理解决数学问题 • 在实际生活中运用三垂线定理及逆定理
重点与难点
•三垂线定理及逆定理的适用条件 •三垂线定理及逆定理的应用

三垂线定理

三垂线定理
【三垂线定理】在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．
已知：PA,PO 分别是平面α的垂线和斜线，AO 是PO 在平面α上的射
影．AO a a ⊥⊂,α．
求证：PO ⊥α．
⎭⎬⎫⊂⊥ααa PA ⇒⎭
⎬⎫⊥⊥a AO a PA PO a PAO PO PAO a ⊥⇒⎭
⎬⎫⊂⊥⇒平面平面
【三垂线定理的逆定理】在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直．
【例１】如果一个角所在平面外一点到角
的两边距离相等，那么这一点在平
面上的射影在这个角的平分线上．
【已知】∠在平面α内，点αα⊥⊥⊥∉PO AC PF AB PE P ,,,,垂足分别是PF PE O F E =,,,
【例2 】点o 是△ABC 的垂心，O P ⊥平面ABC ．求证：PA ⊥BC.
【证明】略。

三垂线定理证明过程

三垂线定理证明过程三垂线定理是解决三角形垂心位置的一个重要定理。

在本文中，我们将通过证明过程来探讨三垂线定理的原理和应用。

让我们来介绍一下三垂线定理的概念。

在任意三角形ABC中，我们可以通过顶点A、B、C分别作边BC、AC、AB的垂线，分别得到D、E、F三个垂足点。

三垂线定理指出，这三条垂线所交于一点H，该点被称为三角形ABC的垂心。

为了证明三垂线定理，我们将分两步进行推理。

首先，我们需要证明垂心H在BC上。

假设垂线AD与BC的交点是H，我们将证明H在BC上。

根据垂直线的性质，可知∠ABH=90°。

同理，由于垂线CE与AB垂直，我们可以得出∠CBH=90°。

因此，∠ABH和∠CBH都是直角，那么∠ABH+∠CBH=180°。

由此可知，点H在直线BC上。

接下来，我们继续证明垂心H在AC和AB上。

我们已经得出点H在BC上，现在我们需要证明H也在AC上。

假设垂线BE和AC的交点是H'，我们将证明H'和H是同一个点。

根据垂直线的性质，可知∠BAH'=90°。

同理，由于垂线CF与AB垂直，我们可以得出∠CAH'=90°。

因此，∠BAH'和∠CAH'都是直角，那么∠BAH'+∠CAH'=180°。

由此可知，点H'在直线AC上。

同样地，我们可以通过证明垂线CF与AB的交点是H来得出结论，点H也在直线AB上。

我们已经证明了三垂线定理。

在任意三角形ABC中，通过连接顶点A、B、C和分别作边BC、AC、AB的垂线，得到的三个垂足点D、E、F所确定的垂心H是在三角形的三条边上的。

三垂线定理在几何学中有着重要的应用。

通过垂心的位置，我们可以推导出很多与三角形相关的性质。

例如，垂心到三角形三边的距离相等，垂心到三个顶点的连线会互相垂直等等。

这些性质可以帮助我们解决许多与三角形相关的问题，如求三角形的面积、判断三角形的类型等。

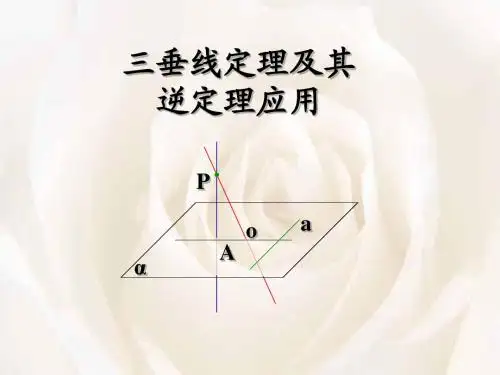
9.4.5三垂线定理及其逆定理

C1
D
E
.
F1
C
A
P
B
三垂线定理
例5、设PA、PB、PC两两互相垂直，且PA = 3，PB = 4， PA、PB、PC两两互相垂直两两互相垂直， 3， 4， PC = 6，求点P到平面ABC的距离。 6，求点P到平面ABC的距离。 ABC的距离 P
解: 作PH⊥平面ABC， PH⊥平面ABC，平面ABC 连AH交BC于E，连PE AH交BC于 ∵PA、PB、PC两两垂直 ∵PA、PB、PC两两垂直 ∴PA⊥平面PBC PA⊥平面平面PBC ∴PA⊥BC
A
D
4
300 O 3 C
α
B
证：作CD ⊥AB BO⊥OC ⊥ CO ⊥面AOB AO ⊥面α 连结OD 由三垂线定理 ∴DO⊥AB ⊥
在Rt△COD中，CD= 15
在Rt△AOD中， OD=AOsin∠DOA= 2 3
例4：已知矩形：已知矩形ABCD中，AB= 3 3 ，BC=3，沿中，对角线BD将折起，移到C′点对角线将△BCD折起，使点移到点，且C′ 折起使点C移到点在平面ABD上的射影恰在上求证（1）上的射影O恰在点在平面上的射影恰在AB上求证（） BC′⊥平面 ⊥平面AD C′ （2）求） 6 到平面B 点A到平面 C′D的距离到平面的距离（3）求直线） AB与平面 C′D所成的角与平面B 与平面所成的角
B A C H E
AH为PA在平面ABC内的射影 AH为PA在平面ABC内的射影在平面ABC ∴BC⊥AH，即BC⊥AE，又AE在平面PBC内的射 BC⊥AH， BC⊥AE， AE在平面PBC内的射在平面PBC 影是PE PE，影是PE， ∴BC ⊥PE 4×6 12 Rt△PBC中在Rt△PBC中，PE= ------ = ---13 42+62 144 2 29 Rt△APE中在Rt△APE中，AE= PA2+PE2= 9+ --- = ---13 13

三垂线定理

三垂线定理
P
Ⅴ. 三垂线定理及其逆定理：

A
O
a
三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直 .
a PA a PO a OA
三垂线逆定理：在平面内的一条直线， a 如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直 .
三垂线定理
Ⅳ. 直线和平面所成的角：
1.斜线(段)及其射影长的有关性质
从平面外一点向这个平面所引的垂线段和斜线段中：
“斜线段长相等射影长相等”
2.直线和平面所成的角
P
[0 ， ] 90
0 此时a // 或a
O
A
PAO为直线PA与平面所成的角
最小角原理：斜线和平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角 .

B . 0 ,

CLeabharlann 0 ， 90

D . ， 180

例 3 . AB 是异面直线 a , b 的公垂线段， AB 2， a , b 成 30 角，在 a 上取点 P 使 AP 4，则点 P 到 b 的距离等于 ( B ) A . 2 2 或 2 14 B .2 2 C . 2 14 D .2 5
PA a OA a PO
三垂线定理
例 1 .设 a , b 是平面外的任意两条直线，则 “ a , b 的长相等” 是“ a , b 在平面内的射影长相等”的
既非充分也非必要 __________ ___ 条件 .

三垂线定理应用

器和皮尺作测量工具，能否求出电塔顶与道路的距离？解：在道边取一点C，使BC与道边所成水平角等于90°，再在道边取一点D，使水平角CDB等于45°，测得C、D的距离等于20cm A
B
90°
C
45°
D
三垂线定理
∵BC是AC的射影
且CD⊥BC
∴CD⊥AC
因此斜线AC的长度就是电塔顶与道路的距离。 ∵∠CDB=45°，CD⊥BC，CD=20cm 答：电塔顶与道路的距离是25m。
三垂线定理：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。已知:PO,PA分别是平面α的垂线,斜线,OA是PA 在 α内的射影,a 求证: a ⊥PA. α,且a ⊥OA.
P
A a O α

三垂线定理的逆定理：在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直。
A
B∴BC=20m， Nhomakorabea在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm)
90°
C
45°
D
证明:∵AH⊥平面BCD，
A
∴BH为斜线AB在
平面BCD上的射影. B ∵AB⊥CD.
∵CD 平面BCD，
D
H C
∴BH⊥CD.
4、在空间四边形ABCD中AB⊥CD, AC⊥BD, A 求证:BC⊥CD
.
B
D
C
二、应用:
1、有一方木料如图,上底有一点E,要经过点E在上底面内画一条直线和C,E的连线垂直,应怎样画?
“一垂二射三证明” “一垂”:找平面及平面的垂线 “二射”:找斜线在平面上的射影 “三证明”:用定理证明直线垂直

三垂直定理立体几何

三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。

在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。

换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。

证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。

点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。

考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。

根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。

将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。

应用：利用三垂线定理，可以方便地计算三角形的面积。

设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。

由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。

三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。

需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。

三垂线定理

如图：请说出下列图形中的垂线、斜线和射影。
P
直线PO是垂线
直线PA是斜线
A α O
a
直线OA是直线PA在平面内的射影
思考：
若 a OA ，直线a和直线PA是什么关系？
新知探究
• 定理证明
α
O
P
已知：PO、PA分别是平面的垂线、斜线， OA是PA在内的射影，a , 且a OA
求证：a PA
且CD⊥BC
∴CD⊥AC(三垂线定理)
因此斜线AC的长度就是电塔顶与道路的距离。 ∵∠CDB=45°，CD⊥BC，CD=20m 答：电塔顶与道路的距离是25m。
A
B
∴BC=20m，
在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(m)
“一垂二射三证”
90°
C
45°
D
三垂线定理及三垂线定理逆定理
A B
应用举例
例2、道旁有一条河，彼岸有电塔AB，高15m，只有测角
器和皮尺作测量工具，能否求出电塔顶与道路的距离？解：在道边取一点C，使BC与道边所成水平角等于90°，再在道边取一点D，使水平角CDB等于45°，测得C、D的距离等于20m A
B
90°
C
45°
D
应用举例
∵BC是AC的射影
（必做）教材 P 68 练习第2、3、 4、5题。（书上，下节评讲）
预习教材 P 68 例一
（选做）预习教材 P 68 第6题
感谢您的莅临指导
a可以移动，但只能在平面内移动。因此，直线a和斜线PA可以相交也可以异面。 3、三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

三垂线定理

P
QLeabharlann CRAB
巩固性练习：
1、若一条直线与平面的一条斜线在此平面上的射影垂直，则这条直线与斜线的位置关系是（ D ）（A）垂直（B）异面（C）相交（D）不能确定 2、在一个四面体中，如果它有一个面是直角三角形，那么 P 它的另外三个面（ C ）（A）至多只能有一个直角三角形（B）至多只能有两个直角三角形（C）可能都是直角三角形 C （D）一定都不是直角三角形 A
南京师范大学附属实验中学
三垂线定理及其逆定理
制作人:
徐慈
制作人：徐慈
三垂线定理
• • • • • • 复习斜线与射影概念三垂线定理三垂线定理证明例题作业
复习（直线与平面的位置关系）
直线在平面内：
l a
l
直线与平面平行：
a
直线与平面相交：
a
l
复习：直线与平面垂直
定义：如果一条直线垂直于平面内所有直线，那么这条直线垂直于这个平面。判定定理：如果平面外一直线与平面内的两条相交（平行）直线垂直，那么这条直线垂直于这个平面。因为两条相交（平行）直线确定一个平面。（重要结论）：如果一条直线垂直于一个平面，那么这条直线垂直于平面内所有直线。
B
本节课作业: P56 3,5,7
别忘了完成作业哦，下节课老师检查呦！
斜线的射影
做法：斜线上任取一点（除斜足外）作该点在平面内的射影点，连结该点和斜足的直线就是斜线在平面内的射影。
平面：a
P
斜线：PO
射影：AO a
A
O
三垂线定理
三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

三垂线定理

线斜垂直
线射垂直
定理逆定理
在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。
三垂线定理的逆定理
在平面内的一条直线，如果和这个平面的一条斜线垂直，那么，它也和这条斜线的射影垂直。
线斜垂直
三垂线定理
对三垂线定理的说明： 1、三垂线定理描述的是PO(斜线)、AO(射影)、 a(直线)之间的垂直关系。 2、a与PO可以相交，也可以异面。 3、三垂线定理的实质是平面的一条斜线和
证明： PO
P
a
a PO
又 a OA
OA PO O
a
A
o
a 面PAO PA 面PAO
a PA
(1)在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。 (2)在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直。
三垂线定理：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。三垂线定理的逆定理：在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直。
P
a
A
o
三垂线定理包含几种垂直关系？
①线面垂直 ②线射垂直 ③ 线斜垂直
P P P O
BC PC
证明： PA 面ABC AC为PC在面内的射影 BC AC
由三垂线定理得： PC BC
三垂线定理例3、如图，已知正方体ABCD-A1B1C1D1中，连结BD1， AC，CB1，B1A，求证：BD1⊥平面AB1C
证明：连结BD，连结A1B ∵ABCD是正方形，∴AC⊥BD 又DD1⊥平面ABCD ∴BD是斜线D1B在平面ABCD上的射影 ∵AC在平面AC内，∴BD1⊥AC 请同学思考：如何证明BD1⊥AB1 而AB1， AC相交于点A且都在平面 AB1C内 ∴BD1⊥平面AB1C

三垂线定理

教师姓名学生姓名学管师学科数学年级上课时间月日：00--- ：00 课题三垂线定理及其逆定理教学目标三垂线定理及其逆定理的应用教学重难点三垂线定理在证明题中的各种应用教学过程知识点：1.三垂线定理；；2.三垂线定理的逆定理；3.综合应用；【知识梳理】1．三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO分别是平面α的垂线和斜线，AO是PO在平面α的射影,,aα⊂a AO⊥。

求证：a PO⊥；证明：说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a与PO可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

aPOAα例1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

PABC例2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

例4.在正方体1AC 中，求证：11111,AC BD AC BC ⊥⊥； OCPBADD 1C 1B 1A 1DCBA2．写出三垂线定理的逆命题，并证明它的正确性；命题：已知：求证：证明：例2．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ∆的垂心；例3.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上已知：求证：aPOAαD A B C FE O αAC P B说明：可以作为定理来用。

例5．已知：Rt ABC ∆中，,3,42A AB AC π∠===，PA 是面ABC 的斜线，3PAB PAc π∠=∠=。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三垂线定理
三垂线定理
在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。
已知 PO、PA分别
是平面的垂线、斜线，OA是PA在平面
上的射影。a ，
a⊥OA。
求证： a⊥PA
P
O
Aa
三垂线定理：在平面
P
内的一条直线，如果和这个平
面的一条斜线的射影垂直，那
么，它就和这条斜线垂直。
判断下列命题的真假：
D1
⑴若a是平面α的斜线，直线b垂直于
a在平面α内的射影，则 a⊥b （ ×）
A1
C1 B1
⑵若 a是平面α的斜线，平面β内
的直线b垂直于a在平面α内的射
影，则 a⊥b
（ ×） D
C
⑶若a是平面α的斜线，直线b α
且b垂直ቤተ መጻሕፍቲ ባይዱa在另一平面β内的射
A
B
影则a⊥b
（× ）面ABCD →面α
三垂线定理的逆理：
在平面内的一条直线，如果和这个平面的一条斜线垂直，那么，它也和这条斜线的射影垂直。
线射垂直
P
P
D1
C1
A
D
O
A
B
C
(1)
(2)
A1 C
D
B1 C
MA
B
B
(3)
(1) PA⊥正方形ABCD所在平面，O为对角线BD的中点，求证：PO⊥BD，PC⊥BD
证明: ∵ABCD为正方形 O为BD的中点
P
A
O B
D C
∴ AO⊥BD
PO⊥BD 又AO是PO在ABCD上的射影
同理，AC⊥BD AC是PC在ABCD上的射影 PC⊥BD
题直线垂直的判定定理，回这两条直线可以是：
顾 ①相交直线
②异面直线
e dc
αA
Ob a
注意：如果将定理中例如：当 b⊥ 时，
“在平面内”的条件
b⊥OA
解去掉，结论仍然成立吗？
但 b不垂直于OP
题
P
b
回顾
直线a 在一定要在平面内，如果 a 不
在平面内，定理就不一定成立。
Oa
αA
练习：
⑷若a是平面α的斜线,b∥α,直线
b垂直于a在平面α内的射影，
则 a⊥b
（√
）面直直面直直面直直A线线线线BA线线B1ABBBAACAB11CC1BDCB11CDCBC→→→→1→→→→斜垂面斜斜垂面面线线α线线线αβ abaab
三垂线定理包含几种垂直关系？
①线面垂直 ②线射垂直 ③ 线斜垂直
O
PO⊥
1 a
PO ⊥a OA⊥a 2
Aa
证明：
a⊥平面PAO
PA平面PAO
a⊥PA
3
三垂线定理
Ⅴ. 三垂线定理及其逆定理：
三垂线定理：在平面内的一条直线，a
如
果
和
这
个平面
的
一
条斜
线
的
射
影垂直
，PA
a
PO
那么它也和这条斜线垂直.
a OA
三垂线逆定理：在平面内的一条直线，a
如果
和
这
个
平
面
的一
条斜
线
垂
直
，
那
么
PA
a
OA
它也和这条斜线的射影垂直.
a PO
例1 已知P 是平面ABC 外一点， PA⊥平面 ABC ，AC ⊥ BC，求证： PC ⊥ BC
P 证明：∵ P 是平面ABC 外一点
PA⊥平面ABC ∴PC是平面ABC的斜线 ∴ ∵ABCC是平PC面在A平BC面且ABACC上⊥的B射C 影A ∴由三垂线定理得
P
P
P
A Oa
A Oa
A Oa
α
α
α
直线和平面垂直
平面内的直线和平面一条斜线的射影垂直
平面内的直线和平面的一条斜线垂直
三垂线定理的逆定理
线射垂直 P
？ P 线斜垂直
A Oa α
平面内的一条直线和平面的一条斜线在平面内的射影垂直
A Oa α
平面内的一条直线和平面的一条斜线垂直
三垂线定理的逆定理
成30角，PA 底面ABCD.
PE
(1)若AE PD于E，求证：BE PD;
G
(2)求异面直线AE、CD所成角的大小. A H
D
B
C
三垂线定理
例4. A为二面角－CD－的棱CD上一点，AB在平
面内且与棱CD成45º角，又AB与平面成30º，求二
面角－CD－的大小。
C AO
B
D
解：作BC于C，连结AC 过C作COCD于O，连结OB
PC ⊥ BC
O
B
C
例2 直接利用三垂线定理证明下列各题：
(1) 已知：PA⊥正方形ABCD所在平面，O为对角线BD的中点求证：PO⊥BD，PC⊥BD
(2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点，求证：BC⊥AM
(3) 已知：在正方体AC1中，求证：A1C⊥B1D1，A1C⊥BC1
P
(2) 已知：PA⊥平面PBC，PB=PC，
M是BC的中点，
求证：BC⊥AM 证明: ∵ PB=PC
M是BC的中点
PM ⊥BC
∵PA⊥平面PBC
C A
M B
BC⊥AM
∴PM是AM在平面PBC上的射影
D1 (3) 在正方体AC1中，
求证：A1C⊥BC1 ， A1C⊥B1D1 A1
证明：∵在正方体AC1中
D
A1B1⊥面BCC1B1且BC1 ⊥B1C A
∴B1C是A1C在面BCC1B1上的射影 D1
由三垂线定理知 A1C⊥BC1
同理可证， A1C⊥B1D1
A1 D
A
C1 B1
C B
C1 B1
C B
三垂线定理
例3.如图，在四棱锥P ABCD的底面ABCD是直角梯形，
BAD 90，AD // BC, AB BC a, AD 2a, PD与底面
C
由三垂线定理可得： BOCD
则 ∠BOC是二面角 CD 的平面角
设AO =a 在RtAOB中，BO=a, AB= 2a
在RtACB中，BAC= 30º, AB=
2a, BC=
2 2
a
在RtBCO中，sin ∠BOC= BC 2
OB 2
∴所求二面角的大小为45º
我们要学会从纷繁的已知条件中找出或者创造出符合三垂线定理的条件，怎么找？
在平面内的一条直线，如果和这个平面的一条斜线垂直，那么，它也和这条斜线的射影垂直。
P
已知：PA，PO分
别是平面的垂线和斜
线，AO是PO在平面
A
O a 的射影,a ,a ⊥PO
α
求证：a ⊥AO
线射垂直定逆定理理线斜垂直
三垂线定理：在平面
内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。
P
解题
α
A
Oa
回
顾 A1
C1 B1
C B
AO a α
PP
C A
M B
三垂线定理解题的关键：找三垂！
怎么找？
解题
一找直线和平面垂直
P
回顾
二找平面的斜线在平面内的射影和平面内的一条直线垂直
α
A Oa
注意：由一垂、二垂直接得出第三垂并不是三垂都作为已知条件
使用三垂线定理还应注意些什么？
解三垂线定理是平面的一条斜线与平面内的 P

三垂线定理

合集下载

三垂线定理及其逆定理

三垂线定理

三垂线定理

三垂线定理

【数学课件】三垂线定理

三垂线定理

三垂线定理证明过程

9.4.5三垂线定理及其逆定理

三垂线定理

三垂线定理应用

三垂直定理立体几何

三垂线定理

三垂线定理

三垂线定理

三垂线定理

文档推荐

最新文档