李亚普诺夫法稳定性分析
- 格式:doc
- 大小:712.00 KB
- 文档页数:31
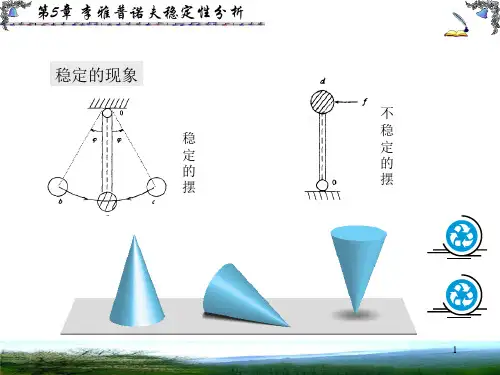



第四章稳定性与李雅普诺夫方法稳定性与李雅普诺夫方法是控制理论中的两个重要概念。
稳定性是控制系统分析中的基本问题之一,它描述了系统在受到干扰后能否回到平衡状态的能力。
李雅普诺夫方法是一种常用的稳定性分析方法,通过构造李雅普诺夫函数来判断系统的稳定性。
稳定性是控制系统设计中最基本的要求之一、一个稳定的系统能够在受到干扰后迅速恢复到平衡状态,而不会发生不可控制的震荡或不稳定的行为。
稳定性可以分为两种类型:渐近稳定性和有界稳定性。
渐近稳定性要求系统的状态能够收敛到一个稳定的平衡点,而有界稳定性要求系统的状态能够保持在一个有限范围内。
李雅普诺夫方法是一种通过构造李雅普诺夫函数来判断系统稳定性的方法。
李雅普诺夫函数是一个标量函数,它满足以下条件:1)对于任意非零的向量,李雅普诺夫函数的导数都是负的或零;2)当且仅当系统达到稳定时,李雅普诺夫函数的导数为零。
通过构造李雅普诺夫函数并分析其导数的符号,可以判断系统的稳定性。
在实际应用中,人们通常使用李雅普诺夫直接法、李雅普诺夫间接法和李雅普诺夫-克拉洛夫稳定性定理等方法来进行稳定性分析。
其中,李雅普诺夫直接法是最常用的方法之一,它通过选择一个合适的李雅普诺夫函数来判断系统的稳定性。
如果可以找到一个李雅普诺夫函数,使得该函数的导数对于所有非零的初始条件都是负的,则系统是渐近稳定的。
李雅普诺夫间接法是通过构造一个李雅普诺夫方程来判断系统的稳定性。
李雅普诺夫方程是一个微分方程,其中包含系统的状态向量和一个非负标量函数,满足一定的条件。
如果可以找到一个满足李雅普诺夫方程的解,并且该解是有界的,则系统是有界稳定的。
李雅普诺夫-克拉洛夫稳定性定理是李雅普诺夫方法的重要理论基础。
该定理表明,如果系统的李雅普诺夫函数存在并且连续可导,并且李雅普诺夫函数的导数满足一定的条件,则系统是渐近稳定的。
这个定理为李雅普诺夫方法的应用提供了重要的理论依据。
总之,稳定性与李雅普诺夫方法是控制理论中基础且重要的概念。


第六章 李雅普诺夫稳定性分析在反馈控制系统的分析设计中,系统的稳定性是首先需要考虑的问题之一。
因为它关系到系统是否能正常工作。
经典控制理论中已经建立了劳斯判据、Huiwitz 稳定判据、Nquist 判据、对数判据、根轨迹判据等来判断线性定常系统的稳定性,但不适用于非线性和时变系统。
分析非线性系统稳定性及自振的描述函数法,则要求系统的线性部分具有良好的滤除谐波的性能;而相平面法则只适合于一阶、二阶非线性系统。
1892年俄国学者李雅普诺夫(Lyapunov )提出的稳定性理论是确定系统稳定性的更一般的理论,它采用状态向量来描述,不仅适用于单变量、线性、定常系统,还适用于多变量、非线性、时变系统。
§6-1 外部稳定性和内部稳定性系统的数学模型有输入输出描述(即外部描述)和状态空间描述(即内部描述),相应的稳定性便分为外部稳定性和内部稳定性。
一、外部稳定性1、定义(外部稳定性):若系统对所有有界输入引起的零状态响应的输出是有界的,则称该系统是外部稳定的。
(外部稳定性也称为BIBO (Bounded Input Bounded Output )稳定性) 说明:(1)所谓有界是指如果一个函数)(t h ,在时间区间],0[∞中,它的幅值不会增至无穷,即存在一个实常数k ,使得对于所有的[]∞∈0t ,恒有∞<≤k t h )(成立。
(2)所谓零状态响应,是指零初始状态时非零输入引起的响应。
2、系统外部稳定性判据线性定常连续系统∑),,(C B A 的传递函数矩阵为Cxy Bu Ax x=+=BUA sI X BU X A sI CX Y BU AX sX 1)()(--==-=+=B A sIC s G 1)()(--=当且仅当)(s G 极点都在s 的左半平面内时,系统才是外部稳定(或BIBO 稳定)的。
【例6.1.1】已知受控系统状态空间表达式为u x x ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=121160 , []x y 10= 试分析系统的外部稳定性。
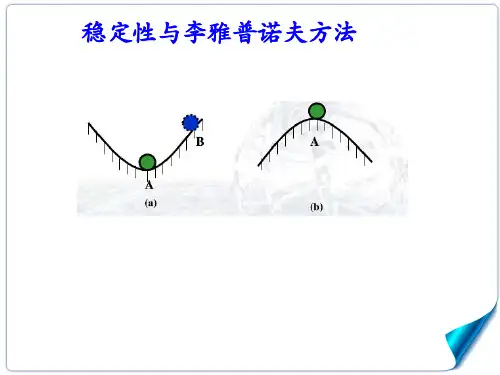




第4章稳定性与李雅普诺夫方法稳定性是评估一个系统的重要性能指标,它描述了系统在一定初始条件下是否能够保持其平衡状态。
稳定性分为两种类型,即渐近稳定性和有界稳定性。
渐近稳定性指的是系统随着时间的推移趋向于其中一平衡状态,而有界稳定性指的是系统在任意时刻的状态都保持在其中一有界范围内。
为了评估系统的稳定性,我们可以利用李雅普诺夫方法。
李雅普诺夫方法是一种通过构造李雅普诺夫函数来判断系统稳定性的方法。
李雅普诺夫函数是一个满足特定条件的函数,它的导数反映了系统状态变化的趋势。
通过对李雅普诺夫函数的导数进行分析,我们可以判断系统在任意时刻的状态是否会向着平衡状态演进。
在利用李雅普诺夫方法进行稳定性分析时,通常需要满足以下条件:1.李雅普诺夫函数必须是正定函数,并且在系统的平衡点上取得最小值。
2.李雅普诺夫函数的导数必须是负定函数,即在系统的平衡点附近的任意一点,李雅普诺夫函数的导数都小于等于零。
如果满足以上条件,那么系统就是渐近稳定的。
反之,如果李雅普诺夫函数的导数是正定函数,那么系统就是不稳定的。
除了判断系统的稳定性外,李雅普诺夫方法还可以用于定量的稳定性分析。
通过分析李雅普诺夫函数的导数的大小,我们可以得到系统状态变化的速度。
如果李雅普诺夫函数的导数越小,那么系统的稳定性就越好。
反之,如果李雅普诺夫函数的导数越大,那么系统的稳定性就越差。
在实际应用中,李雅普诺夫方法广泛应用于控制系统、电路系统和机械系统等领域。
通过利用李雅普诺夫方法进行稳定性分析,我们可以评估系统的稳定性,并对系统进行控制,以保持系统的稳定状态。
总之,稳定性是一个评估系统性能的重要指标,通过利用李雅普诺夫方法可以判断系统的稳定性,并定量地分析系统的稳定性。
李雅普诺夫方法在控制系统、电路系统和机械系统等领域有广泛的应用前景。
第3章李亚普诺夫法稳定性分析第1节基本概念1.系统的平衡状态设系统的齐次状态方程为x=f),(t x若存在状态e x,对所有t都满足0),x exf(==t,则称e x为系统的平衡状态。
一个系统,不一定都存在平衡状态;如存在,也不一定唯一;多个平衡状态,可能连续,也可能孤立。
一般只研究孤立平衡状态。
一般地,0≠e x ,此时可通过平移变换e x x x =-使(,)x f x t =的平衡点0e x =。
故一般只研究0=e x (原点)处的稳定性。
一般地,认为0t t =时刻扰动消失,此时系统初始状态为0e x x ≠。
2.系统的稳定性 系统受到扰动后其状态将偏离原平衡状态e x 。
系统稳定性表示扰动消失后系统在平衡状态(原e x 或新e x )下继续工作的能力。
稳定性是系统的一种内部属性,可采用齐次状态方程),(t x f x = 通过00≠x ,0t t ≥的自由运动进行研究。
稳定性是针对平衡点而言的。
对0≠A 的线性定常系统,只有一个平衡点=0e x ,平衡点的稳定性与系统稳定性是统一的。
对多平衡点系统,不同的平衡点可能具有不同的稳定性,不存在统一的系统稳定性问题,必须逐一分析各平衡点的稳定性。
3.李亚普诺夫关于稳定性的定义状态x到e x的距离(欧几里德范数):2/12211])()[(neneexxxxxx-++-=-ε≤-e xx称为e x的邻域(以e x为中心、ε为半径的超球体)(εsx∈)。
李亚普诺夫关于稳定性的定义:对任意实数0>ε,总存在0),(>tεδ。
当δ<-e xx0时,系统),(t xfx=自0x出发的状态轨迹)(t x(tt≥):1)若满足ε≤-∞→etxxlim,称系统在e x处李亚普诺夫稳定;2)若满足0lim=-∞→etxx,称系统在e x处渐近稳定;3)对任意0x都满足0lim =-∞→e t x x ,称系统在e x 处大范围渐近稳定; 4)如e x 不是李亚普诺夫稳定或渐近稳定的,则称其是不稳定的。
满足渐近稳定的最大范围称为吸引域。
大范围渐近稳定的必要条件是系统只有一个平衡点。
若0),(0>t εδ与0t 无关,称e x 是一致稳定的。
4、其他类型的稳定性定义BIBO 稳定性,完全稳定性等。
第2节 李亚普诺夫第二法(直接法)稳定性定理1.标量函数的定号性设)(x V 为标量函数,且当0=x ,0)(≡x V 。
若对任意Ω∈≠0x (原点附近): 如0)(>x V (0)(<x V ),则称)(x V 为正定(负定)函数; 如0)(≥x V (0)(≤x V ),则称)(x V 为半正定(半负定)函数; 特别情况:设n n R P ⨯∈,t P P =,则x P x x V t =)(∑∑===n i n j j i ij x x p 11j i n j n i i j i ij n i i ii x x p x p ∑+∑==-=>==,1,1122称为二次型标量函数,)(x V 的定号性与P 的定号性相一致。
P 的定号性可有赛尔维斯特准则确定:设),,2,1(n i i =∆为P 的各阶主子行列式,即,111p =∆,,222112112 p p p p =∆,P n =∆则若),,2,1(0n i i =>∆,则0>P ;若)1,,2,1(0-=≥∆n i i ,0=∆n ,则0≥P ;若,0<∆为奇数i ,0>∆为偶数i 则0<P ;若,0≤∆为奇数i ,0≥∆为偶数i 0=∆n ,则0≤P 。
2.直接法稳定性定理 设对),(t x f x = (0>t )的0=e x ,在其某邻域内存在0),(>t x V ,且其沿状态轨迹关于时间的导数为),(t x V,则有 (1)若0),(>t x V,e x 不稳定; (2)若0),(≤t x V,e x 李亚普诺夫稳定; (3)若0),(<t x V,或0),(≤t x V 但对e x x ≠∀),(t x V 不恒等于0,则e x 渐近稳定;且当∞→x 时∞→),(t x V ,则e x 大范围渐近稳定。
此时的),(t x V 称为李亚普诺夫函数,记为),(*t x V 。
说明:(1)),(t x V 仅表示e x 某邻域内局部运动的稳定性。
(2)对非线性系统,没有构造),(*t x V 的通用的方法,这是李氏直接法应用的困难所在。
(3)对稳定的平衡点,也可能一时找不到),(*t x V ,找不到),(*t x V 也不能据此判定其不稳定。
(4)对稳定的平衡点,其),(*t x V 不是唯一的。
(3)对物理系统,),(t x V 可以理解为能量函数,),(t x V则表示能量沿状态轨迹的变化速率。
对渐近稳定的e x ,在e x 处),(t x V 取极小值。
对一般系统,),(t x V 可视为广义能量函数。
例:R-L 电路稳定性分析。
取i x =,系统状态方程为x LR x -= 。
令0=x 得平衡点为0=e x 。
取221)(Lx x V =(电感磁场能量) 而 0)()(2<-=-==Rx x LR Lx x Lx x V )0(≠x 另∞→∞→)(lim x V x ,故0=e x 大范围渐近稳定。
李亚普诺夫函数为),(*t x V =221Lx 。
显然还有 ),(*t x V =2Lx第3节 线性系统稳定性的直接法分析1、特征值稳定判据 线性定常系统x A x = (det 0)A ≠在0=e x 大范围渐近稳定的充要条件是A 的所有特征值均具有负实部。
2、直接法稳定判据 线性定常系统x A x = 在0=e x 大范围渐近稳定的充要条件是对任意给定的正定实对称矩阵Q ,另存在正定实对称矩阵P ,满足李亚普诺夫方程Q PA P A T -=+而系统的李亚普诺夫函数为 x P x x V T =)(证明:充分性。
不妨取x P x x V T =)(,因0>P ,故可保证0)(>x V 。
而x PA x x P A x x P x x P x x V T T T T T +=+=∙ )(x Q x x PA P A x T T T -=+=)(因0>Q ,必有0)(<∙x V ,所以系统在0=e x 大范围渐近稳定。
必要性。
略 对线性定常系统x A x = ,有推论:李亚普诺夫方程T A P PA I +=具有惟一正定对称解矩阵P 与A 阵所有特征值均具有负(正)实部是等价的。
说明:对高阶系统,求解李亚普诺夫方程不是一件容易的事情。
3线性定常系统过渡过程时间的估计引入衰减系数)()(x V x V -=η 定理:设Q 和P 是满足线性定常系统x A x = 的李亚普诺夫方程Q PA P A T-=+ 的正定对称矩阵,则系统自由运动最小衰减系数估计值为)(1min min -=QP λη 其中 )(min ⋅λ表示)(⋅的最小特征值。
从而等效衰减最大时间常数估计值为min max /1η=T 其从某初始状态0x 自由运动到指定状态x 的最大时间估计值则为)()(ln 10min max x V x V t η≤ 说明:上述方法需要计算特征根1min ()QP λ-,且高阶系统估计误差较大。
更有效的方法是误差平方积分法。
4 线性时变连续系统直接法稳定定理设线性时变连续系统状态方程为x t A x )(= 000)(t t x t x ≥= 系统在平衡点0=e x 处大范围渐近稳定的充要条件是对任意给定的连续正定对称矩阵Q (t ),必存在连续正定对称矩阵P (t ),满足黎卡提矩阵微分方程)()()()()()t Q t A t P t P t A t P T -+-=∙( 而系统的李亚普诺夫函数为)()()(),(t x t P t x t x V T= 设系统x t A x )(= ,0t t ≥的状态转移矩阵为0(,)t t Φ,当给定Q (t ),则黎卡提矩阵微分方程的解为ττφττφφφd ),()(),),()(),)(0000⎰-=t t T T t Q t t t t P t t t P ((式中 )(0t P 为黎卡提矩阵微分方程的初始条件。
通过判别P (t )的正定性可判别系统的稳定性。
该定理不便应用,主要具有理论意义。
第4节 非线性系统稳定性分析1、非线性系统稳定性的间接法(第一法)分析对弱非线性系统,可通过平衡点处的线性化系统来判断原非线性系统在该平衡点的稳定性。
设非线性定常系统的齐次状态方程为 ()x f x =()f x 对x 连续可微。
把()f x 在平衡状态e x 作广义泰勒级数展开: ()e e x x f x x +∆=+∆22()()1()2!e e t e x x x x f x f x f x x x x x x ==∂∂=+∆+∆∆+∂∂()()(,)e e e x xf x f x xg x x x =∂=+∆+∆∂式中 1112121222212///()//////n n n n n f x f x f x f x f x f x f x x f x f x f x ∂∂∂∂∂∂⎡⎤⎢⎥∂∂∂∂∂∂∂⎢⎥=⎢⎥∂⎢⎥∂∂∂∂∂∂⎣⎦---雅克比矩阵;22()f x x ∂∂---海赛(Hessian )矩阵;(,)e g x x ∆---高次项。
若高次项满足0()lim 0x g x x ∆→∆→∆则()x f x =在e x x =领域内的(一次近似)线性化方程为xA x ∆=∆ 式中 ()ex x f x A x =∂=∂——雅克比矩阵在e x x =处的值。
不失一般性,设0e x =,则上述线性化方程写为 x Ax =李亚普诺夫第一定理: 设非线性系统()x f x =在其平衡点0e x =附近的线性化状态方程为x Ax =(1)若A 的所有特征根实部为负,则e x 渐近稳定;(2)若A 的特征根中至少有一个实部为正,则e x 不稳定;(3)若A 的特征根至少有一个实部为0,则e x 的稳定性由高次项()g x 决定。
证明:设A 阵所有特征值均具有负(正)实部,则方程TA P PA I +=存在唯一正定对称解矩阵P 。
选择正定标量函数()T V x x Px = 而()T T V x x Px x Px =+()2()t t t x A P PA x g x Px =++2()t t x x g x Px =+2()(1)t t t g x Pxx x x x =式中 负(正)号对应于A 阵所有特征值均具有负(正)实部。
根据0()lim 0x g x x →→的假设,可知在0e x =的邻域内一定有2()(1)0t t g x Pxx x >,这样就有: 当A 阵所有特征值均具有负实部时,()0V x <,非线性系统()x f x =的平衡点0e x =渐近稳定;当A 阵所有特征值均具有正实部时,()0V x >,非线性系统()x f x =的0e x =不稳定。