控制系统李雅普诺夫稳定性分析

如图5-3李雅普诺夫意义下的稳定性示意图
2.古典理论稳定性定义(渐近稳定性)
设 xe 是系统 的一个孤立平衡状态，如果
（1） xe 是李雅普诺夫意义下稳定的；
（2）
则称此平衡状态是渐近稳定的。
2009-08
CAUC--空中交通管理学院
§6-1 李雅普诺夫稳定性定义
- 初始状态 - 平衡状态
图6-2 二维空间渐近稳定性的几何解释示意图
3.内部稳定性与外部稳定性的关系
1)若系统是内部稳定（渐近稳定）的，则一定是外部稳定（ BIBO稳定）的。
2)若系统是外部稳定（BIBO稳定）的，且又是可控可观测的， 则系统是内部稳定（渐近稳定）的。此时内部稳定和外部稳定 是等价的。
2009-08
CAUC--空中交通管理学院
§6-1 李雅普诺夫稳定性定义
(外部稳定性也称为BIBO（Bounded Input Bounded Output ）稳定性)
说明：
（1） 所谓有界是指如果一个函数 ，在时间区间[0，∞] 中，它的幅值不
会增至无穷，即存在一个实常数k ，使得对于所有的t∈ [0 ∞] ，恒有
|h(t)| ≤ k ≤ ∞成立。 （2） 所谓零状态响应，是指零初始状态时非零输入引起的响应。
若对所有t，状态x满足
，故有下式成立:
，则称该状态x为平衡状态，记为
（5-2）
由平衡状态在状态空间中所确定的点 ，称为平衡点。
2.平衡状态的求法
（1）线性定常系统
其平衡状态xe满足Ax=0
A非奇异，则存在唯一的一个平衡状态xe =0 。 （2）非线性系统
方程
的解可能有多个。
2009-08
CAUC--空中交通管理学院

3
第5章 李雅普诺夫稳定性分析
第五章 李雅普诺夫稳定性分析
5.1 李雅普诺夫意义下的稳定性 5.2 李雅普诺夫第一法(间接法) 5.3 李雅普诺夫第二法(直接法) 5.4 线性定常系统的李雅普诺夫稳定性分析
4
第5章 李雅普诺夫稳定性分析
5.1 李雅普诺夫意义下的稳定性
1．自治系统
没有外输入作用时的系统称为自治系统，可 用如下系统状态方程来描述:
如果时变函数V(x,t)有一个正定函数作为下限， 也就是说，存在一个正定函数W(x) ，使得
V ( x ,t) W ( x), V (0,t) 0, t t0
则称时变函数V(x,t)在域S（域S包含状态空间的 原点）内是正定的。
24
第5章 李雅普诺夫稳定性分析
3. 负定函数：如果-V(x)是正定函数，则标量函数 V(x)为负定函数。
则称平衡状态xe在李雅普诺夫意义下是稳定的。
在上述稳定的定义中，实数δ通常与ε和初始时
刻t0都有关，如果δ只依赖于ε ，而和t0的选取无关，
则称平衡状态是一致稳定的。
9
第5章 李雅普诺夫稳定性分析
5. 渐近稳定性
若系统的平衡状态xe不仅具有李雅普诺夫意 义下的稳定性，且有
lim
t
||
x(t;
x0 ,
(s)
则 m(s) 为矩阵A的最小多项式。
注：换言之，矩阵A的最小多项式就是(sI-A)-1
中所有元素的最小公分母。
17
第5章 李雅普诺夫稳定性分析
例5-1（补充）：判断下述线性定常系统的稳定性
0 0 0
x 0 0
0
x
0 0 1
解：1）系统矩阵A为奇异矩阵，故系统存在无穷

线性化的非线性系统。 定理1：线性定常系统的特征值判据 对于系统 x Ax
1)系统的每一个平衡状态是在李雅普诺夫意义下稳定的充要条 件是：系统矩阵A的全部特征值具有非正实部，且具有零实部的 特征值为A的最小多项式的单根。 2)渐近稳定的充要条件是：系统矩阵A的全部特征值具有负实
部，即
Re( i ) 0
5 不稳定性
x2 x(0)
x1
不论δ 取得得多么小，只要在 S ( ) 内有一条从x0 出发的轨迹跨 出 S ( ) ，则称此平衡状态是不稳定的。
二、李雅普诺夫第一法（间接判别法）
李雅普诺夫第一法（间接法） 是利用状态方程解的特性
来判断系统稳定性的方法，它适用于线性定常、线性时变及可
4 大范围(全局）渐近稳定性
当初始条件扩展至整个状态空间，且平衡状态具有渐近稳定性时， 称此平衡状态是大范围渐近稳定的。此时 , S ( ) 。
对于线性定常系统,因为线性系统稳定性与初始条件的 大小无关，所以如果其平衡状态是渐近稳定的,则一 定是大范围渐近稳定的。 但对于非线性系统则不然,渐近稳定性是一个局部性 的概念,而非全局性的概念。
早在1892年,俄国学者李雅普诺夫（Aleksandr Mikhailovich Lyapunov ， 1857 – 1918) 发表题为“运动稳定性一般问题” 的著名文献,建立了关于运动稳定性研究的一般理论。 百余年来,李雅普诺夫 理论得到极大发展,在 数学、力学、控制理论、 机械工程等领域得到广 泛应用。
x2
xe x1 2范数下球域 x1
3） 李雅普诺夫意义下的稳定性 若状态方程 x f ( x, t ) 所描述的系统, 对于任意的>0和任意初始时刻t0,都对 应存在一个实数(,t0)>0, 从任意位于球域S(xe,)的初始状态x0 出发的状态方程的解x都位于球域S(xe, )内,则称系统的平衡状态xe是李雅普 诺夫意义下稳定的。

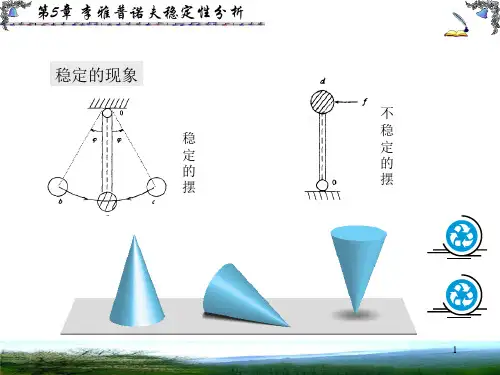
8.3控制系统的李雅普诺夫稳定性分析稳定性描述系统受到外界干扰，平衡工作状态被破坏后，系统偏差调节过程的收敛性。

它是系统的重要特性，是系统正常工作的必要条件。

经典控制理论用代数判据、奈氏判据、对数频率判据、特征根判据来判断线性定常系统的稳定性，用相平面法来判断二阶非线性系统的稳定性，这些稳定性判据无法满足以多变量、非线性、时变为特征的现代控制系统对稳定性分析的要求。

1892年，俄国学者李雅普诺夫建立了基于状态空间描述的稳定性理论，提出了依赖于线性系统微分方程的解来判断稳定性的第一方法（称为间接法）和利用经验和技巧来构造李雅普诺夫函数借以判断稳定性的第二方法（称为直接法）。

李雅普诺夫提出的这一理论是确定系统稳定性的更一般的理论，不仅适用于单变量、线性、定常系统，还适用于多变量、非线性、时变系统，它有效地解决过一些用其他方法未能解决的非线性微分方程的稳定性问题，在现代控制系统的分析与设计中，得到了广泛的应用与发展。

8.3.1 李雅普诺夫稳定性概念忽略输入后，非线性时变系统的状态方程为（8-70） (,)t =&xf x 式中 x —n 维状态向量；T —时间变量；(,)t f x —n 维函数，其展开式为12(,,,,)i i n xf x x x t =&L （n i ,,1L =） 假定方程的解为 ，x 0和t 0 分别为初始状态向量和初始时刻，。

00(;,)t t x x 0000(;,)t t =x x x 1.平衡状态 如果对于所有t ，满足(,)e e t =&xf x =0 （8-71） 的状态x e 称为平衡状态（又称为平衡点）。

平衡状态的各分量不再随时间变化。

若已知状态方程，令 所求得的解x ，便是平衡状态。

0=&x对于线性定常系统，其平衡状态满足=&xAx 0e =Ax ，如果矩阵A 非奇异，系统只有唯一的零解，即存在一个位于状态空间原点的平衡状态。

2.渐近稳定 1）是李氏意义下的稳定
x(t ; x0 , t0 ) xe 0 2）lim t
与t0无关 一致渐进稳定
3.大范围内渐进稳定性
对 x0 s( )
t

都有 lim x(t; x0 , t0 ) xe 0
初始条件扩展到整个空间，且是渐进稳定性。
3.4 李雅普诺夫第二法(直接法)
稳定性定理：
f ( x, t ) 设系统状态方程：x 其平衡状态满足 f (0, t ) 0 ，假定 状态空间原点作为平衡状态( xe 0)，并设 在原点邻域存在V ( x, t )对 x 的连续一阶偏 导数。
定理1：若(1) V ( x, t ) 正定； . (2) V ( x, t ) 负定； 则原点是渐进稳定的。 . 说明： V ( x, t ) 负定 能量随时间连续单调 衰减。 定理2：若(1) V . ( x, t ) 正定； (2) V . ( x, t ) 负半定； (3) V [ x(t ; x0 , t ), t ] 在非零状态不 恒为零，则原点是渐进稳定的。 V ( x) 如果V(x)还满足 lim x
数判据，Nquist稳定判据，根轨迹 判据等
非线性系统：相平面法(适用于一，
二阶非线性系统)
1982年，俄国学者李雅普诺夫提出的
稳定性定理采用了状态向量来描述， 适用于单变量，线性，非线性，定常， 时变，多变量等系统。
应用：自适应，最优控制，非线性控
制等。
主要内容：
李氏第一法（间接法）：求解特征方
程的特征值
李氏第二法（直接法）：利用经验和
技巧来构造李氏函数
2.1 稳定性基本概念
=Ax+Bu(u=0) 1.自治系统：输入为0的系统 x

则状态方程的解为： x(t ) e At x(0) ( R1e1t ... Rnent ) x(0)
Re(i ) 0, (i 1, 2,..., n) lim x(t ) 0, 系统渐近稳定。
t
如果只有一个（或一对）特征值的实部等于0，其余特征值实 部均小于0，则系统仅仅可能是李亚普诺夫意义下的稳定性。
线性定常系统的特征值判据： 系统 x Ax 渐近稳定的充要条件是A的特征值均具有负实 部，即：Re( i ) 0 (i 1,2,, n) 证明：假定A有相异特征值 1 ,..., n 根据凯莱哈密顿定理：矩阵指数eAt为 e1t ,..., ent的线性组合
e At R1e1t ... Rn ent
x xe ( x1 xe1 ) 2 ... ( xn xen ) 2
2
2
2
由范数的定义可知，向量 ( x xe ) 的范数可写成
通常又将 x xe 称为 围之内时，则记为
x 与 xe 的距离。当向量 ( x xe ) 的范数限定在某一范
x xe
0
xe
与经典控制理论的区别： 1. 2. 3. 4. 5. 6. 平衡点/BIBO； 状态稳定/输出稳定； 经典控制的稳定大致对应于现代控制的渐进稳定； 即便输出稳定，状态可能不稳定； 李雅普诺夫意义下的稳定在经典中是不稳定的； 经典控制不需要一致性、全局性概念。
5.2 李雅普诺夫稳定性理论 一、李雅普诺夫第一方法 李雅普诺夫第一法的基本思想是利用状态方程解的性质来 判断系统的稳定性。通常又称为间接法。它适用于线性定常系 统以及线性时变系统和非线性系统可以线性化的情况。
意义：当系统运动到xe点时，系统状态各分量将维持平衡， 不再随时间变化。 平衡点：由系统状态在状态空间中所确定的点 求法：1、线性定常系统

第四章稳定性与李雅普诺夫方法稳定性与李雅普诺夫方法是控制理论中的两个重要概念。

稳定性是控制系统分析中的基本问题之一，它描述了系统在受到干扰后能否回到平衡状态的能力。

李雅普诺夫方法是一种常用的稳定性分析方法，通过构造李雅普诺夫函数来判断系统的稳定性。

稳定性是控制系统设计中最基本的要求之一、一个稳定的系统能够在受到干扰后迅速恢复到平衡状态，而不会发生不可控制的震荡或不稳定的行为。

稳定性可以分为两种类型：渐近稳定性和有界稳定性。

渐近稳定性要求系统的状态能够收敛到一个稳定的平衡点，而有界稳定性要求系统的状态能够保持在一个有限范围内。

李雅普诺夫方法是一种通过构造李雅普诺夫函数来判断系统稳定性的方法。

李雅普诺夫函数是一个标量函数，它满足以下条件：1)对于任意非零的向量，李雅普诺夫函数的导数都是负的或零；2)当且仅当系统达到稳定时，李雅普诺夫函数的导数为零。

通过构造李雅普诺夫函数并分析其导数的符号，可以判断系统的稳定性。

在实际应用中，人们通常使用李雅普诺夫直接法、李雅普诺夫间接法和李雅普诺夫-克拉洛夫稳定性定理等方法来进行稳定性分析。

其中，李雅普诺夫直接法是最常用的方法之一，它通过选择一个合适的李雅普诺夫函数来判断系统的稳定性。

如果可以找到一个李雅普诺夫函数，使得该函数的导数对于所有非零的初始条件都是负的，则系统是渐近稳定的。

李雅普诺夫间接法是通过构造一个李雅普诺夫方程来判断系统的稳定性。

李雅普诺夫方程是一个微分方程，其中包含系统的状态向量和一个非负标量函数，满足一定的条件。

如果可以找到一个满足李雅普诺夫方程的解，并且该解是有界的，则系统是有界稳定的。

李雅普诺夫-克拉洛夫稳定性定理是李雅普诺夫方法的重要理论基础。

该定理表明，如果系统的李雅普诺夫函数存在并且连续可导，并且李雅普诺夫函数的导数满足一定的条件，则系统是渐近稳定的。

这个定理为李雅普诺夫方法的应用提供了重要的理论依据。

总之，稳定性与李雅普诺夫方法是控制理论中基础且重要的概念。

0s
0
1
s
0 1 1 1 1
(s
s 1 1)(s 1)
s
1 1
可见传递函数的极点 s 1位于s的左半平面，故系统
输出稳定。这是因为具有正实部的特征值2 1 被系统的零
点 s 1 对消了，所以在系统的输入输出特性中没被表现出
来。由此可见，只有当系统的传递函数W(s)不出现零、极
点对消现象，并且矩阵A的特征值与系统传递函数W(s)的
2020/3/22
6
现代控制理论
第4章 李亚普诺夫稳定性分析
4.2 李亚普诺夫第二法的概述
1892年俄国学者李亚普诺夫发表了《运动稳定性一般 问题》，最早建立了运动稳定性的一般理论，并把分析常 微分方程组稳定性的全部方法归纳为两类。第一类方法先 求出常微分方程组的解，而后分析其解运动的稳定性，称 为间接方法；第二类方法不必求解常微分方程组，而是提 供出解运动稳定性的信息，称为直接方法，它是从能量观 点提供了判别所有系统稳定性的方法。
即Xe f ( X e ,t) ，0 则把 叫X e做系统的平衡状态。
对于线性定常系统 X AX而言，其平衡状态满足
Xe AX e ，0 若A是非奇异矩阵，则只有 X e ，0 即对线性系 统而言平衡状态只有一个，在坐标原点；反之，则有无限
多个平衡状态。
对于非线性系统而言，平衡状态不只一个。
2020/3/22
9
现代控制理论
第4章 李亚普诺夫稳定性分析
3、李亚普诺夫第二法
李亚普诺夫第二法建立在这样一个直观的物理事实上：
如果一个系统的某个平衡状态是渐近稳定的，即
im
t
X
X，e 那么随着系统的运动，其储存的能量将随时间

稳定性是一个自动控制系统正常工作的首要、必 要条件，是一个重要特征。
要求：
在受到外界扰动后，虽然其原平衡状态被打破， 但在扰动消失后，仍然能恢复到原来的平衡状态， 或者趋于另一平衡状态继续工作。
4
引言
俄国学者李雅普诺夫 Lyapunov （1857－1918）
1892年在博士论文中提出稳定性 理论 ----不仅适用于单变量线性系统， 还适用于多变量、非线性、时变 系统，是确定系统稳定性的更一 般性理论。 1907（15年后）出版了法文版 1992（100年后）出版了英文版 当今任何一本控制期刊都有李雅 普诺夫的名字。
表示始于初态x0的一个运 动或一条状态轨迹 只需考虑自治系统（因为 稳定性是系统在自由运动 下的特性）：
2、初态： x f ( x, t ) 的解为 x(t , x0 , t0 )
x(t0 , x0 , t0 ) x0 初态
8
3、平衡状态
对系统
f ( x, t ) x
n维状态 向量
xt; x0 , t0 xe
f x, t由初态 表明齐次方程 x 扰动所引起的自由响应是有界的

x或短暂 0
15
2、李雅普诺夫（李氏）意义下的稳定性
f ( x, t ) x 设系统 x e f ( xe , t ) 0
如果对每个实数 0 都对应存在另一个 实数 ( , t0 ) 0 ，使得满足
三个平衡 状态
0 xe2 1
10
xe 1 0
0
0 xe3 1
3）线性系统在平衡点稳定，则系统稳定； 而非线性系统在平衡点稳定，则只是在该点稳定， 而不是整个系统稳定----可见，稳定性问题是相对 于平衡状态而言的。 4）线性系统的稳定性只取决于系统的结构和参数， 而与系统的初始条件及外界扰动的大小无关； 但非线性系统的稳定性出了与系统的结构和参数有 关外，还与初始条件及外界扰动的大小有关。

✓
线性定常系统的有界输入有
界输出(BIBO)稳定性
未研究系统的内部状态变化的稳定性，也不能推广 到时变
系统和非线性系统等复杂系统。
➢ 再则，对于非线性系统或时变系统，虽然通过一些 系统转化方法，上述稳定判据尚能在某些特定系统和范 围内应用，但是难以适用于一般系统。
现代控制系统的结构比较复杂，大都存在非线性或时变因 素，即使是系统结构本身，往往也需要根据性能指标的要 求而加以改变，才能适应新的情况，保证系统的正常或最 佳运行状态。
Lyapunov的博士论文被译成法文并于1907年发表，1949年 普林斯顿大学出版社重印了法文版。1992年在Lyapunov的 博士论文发表100周年之际，International Journal of Control （国际控制杂志）以专辑形式发表了Lyapunov论文的英译 版，以纪念他在控制理论领域所作的卓越贡献。
➢ 该方法不仅可用于线性系 统而且可用于非线性时变 系统的分析与设计，已成 为当今控制理论课程的主 要内容之一。
➢ 百余年来Lyapunov理论 得到极大发展, 在数学、 力学、自动控制、机械工 程等领域得到广泛应用。
A.M. Lyapunov是一位天才的数学家。曾从师于大数学家 P.L. Chebyshev（切比雪夫），和A.A. Markov（马尔可夫 ）是同校同学（李比马低两级），并同他们始终保持着良好 的关系。他们共同在概率论方面做出了杰出的贡献。在概率 论中可以看到关于矩的马尔可夫不等式、切比雪夫不等式和 李亚普诺夫不等式等。Lyapunov还在相当一般的条件下证 明了中心极限定理。
✓
经典控制理论讨论的有界输入
有界输出（BIBO）稳定即为外部稳定性 。
Outer stability

说明：
x 1、对于线性定常系统： e f ( xe ) Axe 0
A为非奇异阵时，xe=0是其唯一的平衡状态。 A为奇异阵时，系统有无穷多个平衡状态。 2、对于非线性系统，有一个或多个平衡状态。 3、对任意孤立的 x e 0 ，总可经过一定的坐标变换，把它化 到坐标原点（即零状态）。一般将平衡状态取为状态空间 原点。
经典控制理论 (线性系统） 李氏意义下 不稳定 Re(s)>0 不稳定 临界情况 Re(s)=0 稳定 （极限环，不超出 某个球域即可） 稳定 Re(s)<0 渐近稳定
2012-6-26
13
[本节小结]： 1、平衡状态定义、求法
2、李氏稳定性概念
1）稳定、一致稳定。 2）渐近稳定、一致渐近稳定。 3）大范围渐近稳定。 4）不稳定。
如果
p ik p ki
，则称P为实对称矩阵。
V (x) 0
1）正定性：当且仅当x=0时，才有
；对任意 ；对任意非
非零X，恒有
零x,恒有
2012-6-26
2012-6-26 10
渐近稳定比稳定更重要，但它是一个局部概念，平衡状态局 部稳定并不意味着整个系统能正常工作。确定其渐近稳定的 最大区域很重要。
3、大范围渐近稳定
如果对状态空间的任意点，不管初始偏差有多大（即从状态 空间中所有初始状态出发的轨迹），都有渐近稳定特性。即：
lim x x e 0
1、函数 h ( t ) 有界含义： 对于函数 h ( t )，在 0 , 时间区间内存在实常数 k ，满足 h ( t ) k 。
2、尽管在定义时提到了输入和扰动作用，但对线性定常系统来 说，系统稳定与否完全取决于系统本身的结构和参数，稳定性 是系统本身的一种特性，而与输入作用无关。

5.6.3 二次型最优控制问题现在我们来研究最优控制问题。

已知系统方程为Bu Ax x+= (5.20) 确定最优控制向量)()(t Kx t u -=(5.21) 的矩阵K ，使得性能指标(5.22)达到极小。

式中Q 是正定（或正半定）Hermite 或实对称矩阵，R 是正定Hermite 或实或实对称矩阵。

注意，式(5.22）右边的第二项是考虑到控制信号的能量损耗而引进的。

矩阵Q 和R 确定了误差和能量损耗的相对重要性。

在此，假设控制向量)(t u 是不受约束的。

正如下面讲到的，由式(5.21）给出的线性控制律是最优控制律。

所以，若能确定矩阵K 中的未知元素，使得性能指标达极小，则)()(t Kx t u -=对任意初始状态x (0)而言均是最优的。

图5.6所示为该最优控制系统的结构方块图。

图5.6 最优控制系统现求解最优控制问题。

将式(5.21）代入式(5.20），可得()xAx BKx A BK x =-=- 在以下推导过程中，假设BK A -是稳定矩阵，BK A -的所有特征值均具有负实部。

将式(5.21）代入（5.22），可得⎰⎰∞∞+=+=0)()(xdtRK K Q x dtRKx K x Qx x J H H H H H依照解参数最优化问题时的讨论，取⎰∞+=0)(dtRu u Qx x J HH)()(Px x dtd x RK K Q x HH H -=+ 式中的P 是正定的Hermite 或实对称矩阵。

于是])()[()(x BK A P P BK A x x P x Px xx RK K Q x H H H H H H -+--=--=+ 比较上式两端，并注意到方程对任意x 均应成立，这就要求)()()(RK K Q BK A P P BK A H H +-=-+-(5.23)根据Lyapunov 第二法可知，如果BK A -是稳定矩阵，则必存在一个满足式(5.23）的正定矩阵P 。

1）V(x) ＞ 0，则称V(x)为正定。例如V(x)=x12 +x22； 2）V(x) ≥ 0，则称V(x)为半正定（或非负定）。例如
V(x)=(x1 +x2)2； 3）V(x) ＜ 0，则称V(x)为负定。例如V(x)=－(x12 +2x22)； 4）V(x) ≤ 0，则称V(x)为半负定（或非正定）。例如
p
Δ1
p11 ， Δ2
11
p
21
p
12
p
，…
， Δn P
22
矩阵 P（或 V(x)）定号性的充要条件是：
1）若 Δi 0, i (1,2,, n) ，则 P（或 V(x)）为正定；
2）若
Δi
0, 0,
i为偶数 i为奇数
，则
P（或
V(x)）为负定；
3）若
Δi
0, 0,
i i
(1,2,, n
需要根据舍弃旳髙 阶项再分析 采用李雅普诺夫第 二法
举例：用李雅普诺夫第一法判断下列系统旳稳定性
x1 x1 x1x2
x2
x2
x1x2
第一步：令 x1 0, x2 0
求得系统旳平衡状态 x1e (0,0)T , x1e (1,1)T
第二步：将系统在平衡状态x1e附近线性化
f1 f1
（1）V(x)是满足稳定性判据条件的一个正定的标量函数，且 对于 x 应具有连续的一阶偏导数； （2）对于一个给定系统，如果 V(x)可以找到，那么通常是非 唯一的，这并不影响结论的一致性。 （3）V(x)的最简单形式是二次型函数 V(x) = xTP x，其中 P 为 实对称方阵，它的元素可以是定常的或时变的。但 V(x)并不一 定都是简单的二次型。 （4）如果 V(x)为二次型，且可表示为：

２）如果ｘｅ＝０为系统的平衡状态，则李氏函数应满足Ｖ（ｘｅ）＝ Ｖ（０）＝０。但当ｘ（ｔ）≠ ０
时， 不管其分量大于零或小于零，均能使Ｖ（ｘ）＞０。
基于上述的性质，人们常以状态矢量ｘ的二次型函数Ｖ（ｘ）作为李氏函数
的候选函数，即
式中，ｘ为实变数矢量。只要矩阵Ｐ是正定的，则上式所示的Ｖ（ｘ）就符 合对李氏函数性质的要求。
对于连续定常系统，李雅普诺夫第二方法是根据Ｖ（ｘ）和
的性
质去判别它的稳定性。因此需要研究以下两个问题：
１）具备什么条件的函数才是李雅普诺夫函数，简称李氏函数。
２）怎样利用李氏函数去判别系统平衡状态的稳定性？
由对图10-2所示系统的讨论，可知李氏函数必须要同时具有如下两个性质：
１）李氏函数是自变量为系统的状态矢量ｘ（ｔ）的标量函数。
态是不稳定的。
2021/6/18
第十章 李雅普诺夫稳定性分析
6
为了能更直观地理解上述平衡状态稳定性的概念，
下图在二维状态平面上分别画出了系统平衡状态的稳 定、渐近稳定和不稳定３种情况。
2021/6/18
第十章 李雅普诺夫稳定性分析
7
自动控制理论
第二节 李雅普诺夫第二方法
正定函数
2021/6/18
11
自动控制理论
由上式可见，除了ｘｅ＝０外，系统的能量Ｖ（ｘ）在运动过程中由于 受到了阻尼器的阻尼作用而不断地减小，最后使Ｖ（ｘ）＝０。这个例子很 容易把能量函数Ｖ（ｘ）与实际系统联系起来。然而，对一般的系统而言， 至今还没有一个普遍适用“能量函数” 的表达式。对此，李雅普诺夫提出了 一个虚拟的能量函数，人们称它为李雅普诺夫函数，用Ｖ（ｘ）表示。
则称系统的平衡状态ｘｅ是渐近稳定的。

向量和矩阵的范数
1、向量空间上的欧几里德范数（即向量长度）
其欧几里德范数定义为：
一般
一、向量和矩阵的范数
预备知识
矩阵范数
矩阵 的范数定义为：
【例】
Hale Waihona Puke ， 则即:矩阵每个元素平方和开根号
预备知识
2、矩阵范数
1．二次型函数：由n个变量
组成的二次齐次多项式，称（n元）二次型函数
2．二次型函数的矩阵表示
则系统在原点处的平衡状态是不稳定的。
为唯一的平衡状态。
定理4：设系统状态方程为
李雅普诺夫主要的稳定性定理
例题
[例] 设系统状态方程为
试确定系统的稳定性。
解 xe=0
,
是该系统惟一的平衡状态。
由于当
时
,所以系统在原点处的平衡状态是
大范围渐近稳定的。
选取
李雅普诺夫主要的稳定性定理
例题
[例] 已知定常系统状态方程为
定义：若所有有界输入引起的零状态响应输出有界，则称系统为有界输入输出稳定。
李雅普诺夫第一方法—间接法
定理3：连续定常系统 传递函数为： 系统 BIBO 稳定的充要条件为：传递函数的所有极点均位于S左半平面。
【例】试分析系统渐近稳定和BIBO稳定。
李雅普诺夫主要的稳定性定理
讨论续
这是一个矛盾的结果,表明
也不是系统的
受扰运动解。综合以上分析可知,
当
时,显然有
根据定理9-12可判定系统的原点平衡状态是大范围渐近稳定的。
李雅普诺夫主要的稳定性定理
线性系统稳定性分析
一.线性定常系统李雅普诺夫稳定性分析
线性定常连续系统
系统状态方程为

只在李雅普诺夫意义下稳定，但不是渐近稳定旳系统则称临界 稳定系统，这在工程上属于不稳定系统。
经典控制理论(线性系统）不稳定 (Re(s)>0) 临界情况 (Re(s)=0) 稳定 (Re(s)<0)
Lyapunov意义下
不稳定
稳定
渐近稳定
2024/10/11
25
4.3 李雅普诺夫第一法
2024/10/11
x描述了系统在n维状态空间中从初始条件(t0,x0)出发旳一条状 态运动旳轨线，称系统旳运动或状态轨线
2024/10/11
15
平衡状态
若系统存在状态向量xe，对全部t，都使： f (xe , t) 0
成立，则称xe为系统旳平衡状态。
对于一种任意系统，不一定都存在平衡状态，有时虽然存在也 未必是唯一旳。
早在1892年，俄国数学家李雅普诺夫就提出将鉴定系统稳定性 旳问题归纳为两种措施：李雅普诺夫第一法和李雅普诺夫第二 法。
前者是经过求解系统微分方程，然后根据解旳性质来鉴定系统 旳稳定性。它旳基本思想和分析措施与经典理论是一致旳。
2024/10/11
3
本章要点讨论李雅普诺夫第二法。
它旳特点是不求解系统方程，而是经过一种叫李雅普诺夫函数旳 标量函数来直接鉴定系统旳稳定性。
所以，它尤其合用于那些难以求解旳非线性系统和时变系统。
李雅普诺夫第二法除了用于对系统进行稳定性分析外，还可用于 对系统瞬态响应旳质量进行评价以及求解参数最优化问题。
另外，在当代控制理论旳许多方面，例如最优系统设计、最优 估值、最优滤波以及自适应控制系统设计等，李雅普诺夫理论 都有广泛旳应用。
2024/10/11
所以，怎样拟定渐近稳定旳最大区域，而且尽量扩大其范围是 尤其主要旳。

控制系统中的稳定性分析方法稳定性是控制系统设计和分析中至关重要的概念，它决定了系统的响应是否会随时间或外部干扰的变化而发散或者衰减。

稳定性分析是评估系统的稳定性并识别可能导致系统不稳定的因素的过程。

掌握稳定性分析方法对于设计和优化控制系统至关重要，本文将介绍几种常用的稳定性分析方法。

1. 时间域稳定性分析方法时间域稳定性分析方法是通过研究控制系统的时间响应来评估其稳定性。

其中，最常用的方法是研究系统的阶跃响应。

阶跃响应可以模拟当系统受到单位阶跃输入时的行为。

通过分析阶跃响应中的振荡和衰减情况，可以判断系统的稳定性。

常见的时间域稳定性分析方法包括：- 稳定性判据法：根据控制系统的特征方程的根在左半平面的个数确定系统的稳定性。

例如，系统的特征方程所有根的实部都小于零，则系统是稳定的。

- 跟踪法：通过分析阶跃响应的振荡情况，如超调量和调整时间，来评估系统的稳定性。

例如，当系统的超调量小于一定阈值并且调整时间满足要求时，可以认为系统是稳定的。

2. 频域稳定性分析方法频域稳定性分析方法是通过研究系统的频率响应来评估其稳定性。

频率响应可以揭示系统对不同频率信号的传递特性。

常用的频域稳定性分析方法包括：- Nyquist稳定性判据：根据系统的开环传输函数在复频域上的轨迹来判定系统的稳定性。

如果系统的开环传输函数的轨迹不绕复平面的-1点（-1+j0）（即Nyquist轨迹）或者经过-compensation的选择，可以判定系统是稳定的。

- 辐角判据：通过分析系统的相位频率特性曲线，判断系统的辐角是否满足稳定性条件。

如果系统的相位频率特性曲线满足一定的条件，例如相位频率特性曲线的最大幅值小于180度，则系统可以被认定为是稳定的。

3. Lyapunov稳定性分析方法Lyapunov稳定性分析方法是利用李雅普诺夫函数及其性质来评估系统的稳定性。

李雅普诺夫函数是一个具有良好性质的函数，可以确定系统状态的稳定性行为。

通过构建李雅普诺夫函数，并根据其形式和性质对系统进行分析，确定系统的稳定条件。