下载文档原格式
离散序列的傅里叶变换离散序列的傅里叶变换（Discrete Fourier Transform，简称DFT）是一种将离散序列从时域转换到频域的数学工具。
它在信号处理、图像处理、通信等领域扮演着重要角色。
本文将介绍离散序列的傅里叶变换的基本概念、性质以及在实际应用中的一些例子。
一、离散序列的傅里叶变换的基本概念离散序列的傅里叶变换是将一个离散序列转换为一系列复数的运算。
它的定义公式为：X(k) = Σx(n)e^(-j2πkn/N)其中，X(k)为频域上的复数序列，表示原始序列在频率为k的分量上的幅度和相位信息；x(n)为时域上的离散序列，表示原始序列在时间点n上的取值；N为序列的长度；e为自然对数的底数，j为虚数单位。
二、离散序列的傅里叶变换的性质离散序列的傅里叶变换具有一些重要的性质，包括线性性、平移性、对称性等。
1. 线性性：对于离散序列x(n)和y(n)，以及任意常数a和b，有DFT(ax(n) + by(n)) = aDFT(x(n)) + bDFT(y(n))。
2. 平移性：如果将离散序列x(n)平移m个单位，则其傅里叶变换为X(k)e^(-j2πkm/N)。
3. 对称性：如果离散序列x(n)是实数序列且长度为N，则其傅里叶变换满足X(k) = X(N-k)。
三、离散序列的傅里叶变换的应用举例离散序列的傅里叶变换在实际应用中有着广泛的应用。
以下是几个常见的例子：1. 信号处理：在音乐、语音、图像等信号处理领域，离散序列的傅里叶变换可以用来分析信号的频谱特性，包括频率成分、能量分布等。
通过傅里叶变换，我们可以将时域上的信号转换为频域上的信号，从而更好地理解信号的特征。
2. 图像处理：在图像处理中，离散序列的傅里叶变换可以用来进行图像的滤波、增强、压缩等操作。
通过将图像转换到频域上，我们可以对不同频率分量进行处理，从而实现对图像的各种操作。
3. 通信系统：在通信系统中，离散序列的傅里叶变换可以用来实现信号的调制、解调、滤波等功能。
离散傅里叶变换及其快速算法离散傅里叶变换（Discrete Fourier Transform，DFT）是一种将离散信号转换为频域表示的数学工具。
它在信号处理、图像处理、通信等领域有广泛的应用。
而快速傅里叶变换（Fast Fourier Transform，FFT）是一种能够高效计算DFT的算法，大大减少了计算量。
首先，我们来看一下DFT的原理。
给定一个有限长度的离散信号序列x(n)，DFT将其转换为频谱X(k)，其中k为频率索引，取值范围为0到N-1，N为序列的长度。
DFT的定义公式如下：X(k) = Σ x(n) * exp(-j * 2π * nk / N)其中，exp为自然指数函数，j为虚数单位。
DFT将信号分解为了N个复数的和，这些复数代表了不同频率分量在信号中的贡献。
然而，直接计算DFT的时间复杂度非常高，为O(N^2)。
为了提高计算效率，Cooley和Tukey于1965年提出了FFT算法。
FFT算法基于以下性质：若N为2的整数次幂，则DFT可以被分解为两个较小长度的DFT的线性组合。
具体来说，将N个点的DFT拆分为长度为N/2的两个DFT，然后再对这两个子序列进行DFT，最后将两个子序列的结果组合起来。
这个过程可以递归地进行，直到序列长度为1，即可得到最终的DFT结果。
FFT算法的时间复杂度为O(NlogN)，远远小于直接计算DFT的复杂度。
这使得FFT成为了处理大规模数据的首选方法之一、此外，FFT还有其他一些优点，如可并行化计算、对称性质等。
FFT算法可以采用不同的实现方式，最著名的是基于蝶形运算的Cooley-Tukey算法。
这种实现方式将FFT过程分为了两个阶段：置换阶段和蝶形运算阶段。
置换阶段通过将信号重新排序，将原始序列分为奇偶两个子序列，并计算每个子序列的DFT。
这个过程可以递归地应用于子序列，直到长度为1蝶形运算阶段是FFT算法的核心部分。
蝶形运算是指将两个频域上的复数进行运算，得到新的复数。
离散序列的傅里叶变换及其快速算法（DFT ）单位冲激函数的傅里叶变换：-=-(e )=[n]jw jwnn H h e ∝∝∑ 这是离散傅里叶变换，它是一个以2π为周期的函数。
也可以看成是周期信号(e )jw H 在频域内展开的傅里叶级数，其中h[n]是傅里叶系数。
由Z 变换的定义可得：(e )jw H =H(z),当z=e jw 时。
也就是说傅里叶变换等于仅在单位圆上取值的Z 变换。
信号在时域的能量与在频域的能量是相等的，因为是同一个信号，只是用不同的角度描述。
DTFT 是离散时间序列的傅里叶变换，其时域是离散的，谱是周期的，但还是连续的，仍然不能用计算机处理，因为计算机要求时域和频域都是离散的，实际上要求时域和频域都既是离散的，也是周期的。
时域的连续非周期信号对应频域的连续非周期谱（FT ）时域的连续周期信号对应频域的离散谱。
（FST ）时域是离散的对应频域是周期谱。
（DTFT ）时域离散周期对应频域离散周期。
（DFT ）DFT 中，变换的两边都是离散的，从而才是真正能用计算机来处理的数字信号变换对。
两边都是周期的，处理可以在一个周期内进行。
有两层含义：一是所做的处理是有限的，而是一个周期可以包含全部信息。
信号的离散周期化：工程中的实际信号是连续非周期的，为了进行DFT ，就必须将其离散周期化。
离散化就是采样的过程；周期化分为两种：有限长序列，长度为N ，则可以将该N 点序列看成是周期信号的一个周期；无限长序列，截为N 点。
为了能让计算机处理，需要将时域的连续信号非周期信号做处理，首先用一个冲击串和时域信号相乘，这样得到一个离散的非周期信号(在频域对应的是连续的周期信号)，在对时域的离散非周期信号作周期延拓，则在时域得到一个离散的周期信号(同时，频域也是一个离散的周期信号)。
这就为DFT 做好了准备。
DFT 的定义：2-1-1-=0=0()=[]=[]W N N j nk nk N N N N X k x n ex n π∑∑反变换： 2-1-1-=0=011[]=(k)=()N N j nk nk N N k k x n X e X k W N N π∑∑ 其中： 2-=j N N W eπ特别注意： 2=w k Nπ 2--==j k k jw N N W e e π这是一个以N 为周期的信号，每经过N 点，在单位圆上转一圈。
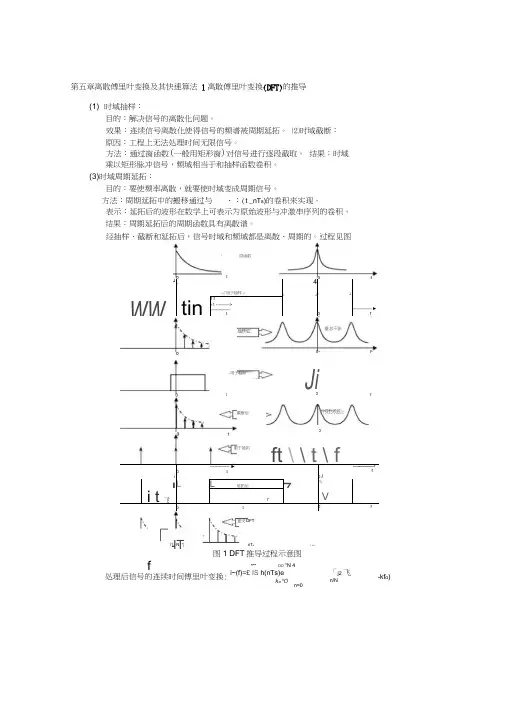
第五章离散傅里叶变换及其快速算法 1离散傅里叶变换(DFT)的推导(1) 时域抽样：目的：解决信号的离散化问题。
效果：连续信号离散化使得信号的频谱被周期延拓。
⑵时域截断： 原因：工程上无法处理时间无限信号。
方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。
结果：时域乘以矩形脉冲信号，频域相当于和抽样函数卷积。
(3)时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。
方法：周期延拓中的搬移通过与 、：(t _nT s )的卷积来实现。
表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。
结果：周期延拓后的周期函数具有离散谱。
经抽样、截断和延拓后，信号时域和频域都是离散、周期的。
过程见图抽样后0 fJif-用于截断原函数J L<Z 用于抽样i4LJI Ji WWtin1 f=1 ----------> --------------t-------------- ►fVtt截断后有卷积波纹i------------- ►t0 I------------------ rfJL 」L延拓后7角ii t飞7Vtfft \ \ t \ f定义DFT用于延拓「ITf处理后信号的连续时间傅里叶变换:I'U N *|nT sr 0 N图1 DFT 推导过程示意图〜 oo "N 4l ~(f)=£ IS h(nTs)ek =^O「j2 飞n/Nn=0-kf o )(i) l~(f)是离散函数，仅在离散频率点f二kf o k—处存在冲激，强度为a k,其T o NT s余各点为0。
〜N N 1(ii) H(f)是周期函数，周期为Nf o == 工，每个周期内有N个不同的幅值。
T o NT s T s(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。
2 DFT及IDFT的定义DFT定义：设hnT s是连续函数h(t)的N个抽样值n=0,1,…,N J，这N个点的宽度为N 的DFT 为：DFT N h(nT s)]=^ h(nT s)e」2邢/N =H —— J (k =0,1,…，N _1)7 l NT s 丿IDFT定义：设H 上是连续频率函数H(f)的N个抽样值k =0,1，…，N J，这N个点(NT s 丿的宽度为N的IDFT为：DFT N1 H k丄7 H L e」2「nk/N厶nTs , (k =0,1,…，N —1)|L Ns N k 卫NT se^Rk/N称为N点DFT的变换核函数，e j2 flk/N称为N点IDFT的变换核函数。
分治法：快速傅里叶变换算法学院：网研院 姓名：xxx 学号：xxx一、 分治法原理分治法是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。
分治法的精髓：◆ 分--将问题分解为规模更小的子问题； ◆ 治--将这些规模更小的子问题逐个击破；◆ 合--将已解决的子问题合并，最终得出“母”问题的解； 二、 快速傅里叶变换（FFT ）简介快速傅里叶变换（Fast Fourier Transform, FFT ），是离散傅里叶变换的快速算法，也可用于计算离散傅里叶变换的逆变换。
它是根据离散傅里叶变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。
快速傅里叶变换有广泛的应用，如数字信号处理、计算大整数乘法、求解偏微分方程等等。
序列的离散傅里叶变换公式为：令 则上式可写为：从算法分析角度：于是：分别考虑对其奇数项和偶数项作傅氏变换： 则从而，可以将对N 个量的傅氏变换变成为对两个规模更小的序列的变换。
这样，将变换的量大大减小。
快速傅里叶变换是分治法的一种具体实现。
[][]()∑-=-=102N n N jnk e n x k X π1,,0]},[{-=N i i x Nj N e W π2-=∑-==10][][N n knNW n x k X kn NNn N n nk N N n kn N W n x W n x W n x k X )12(12012210]12[]2[][][+-=-=-=∑∑∑⋅++⋅==nkN N n N n nk N E W n x W n x k X 2/12122]2[]2[][∑∑-=-=⋅=⋅=knN N n N n nk N O W n x W n x k X 2/1201202]12[]12[][∑∑-=-=⋅+=⋅+=][][][][10k X W k X W n x k X O k N E N n kn N ⋅+==∑-=三、 快速傅里叶变换算法FFT1. 算法● 输入采样值；● 对采用值进行补0操作，使采样值的个数是2的幂次；● 对补0后的序列进行重排，重排的原则是按照序列的下标奇偶性排序，先偶后奇，分成两个子序列，然后对子序列继续重排。
