基于Simulink控制系统的稳态误差分析
- 格式:doc
- 大小:286.00 KB
- 文档页数:3
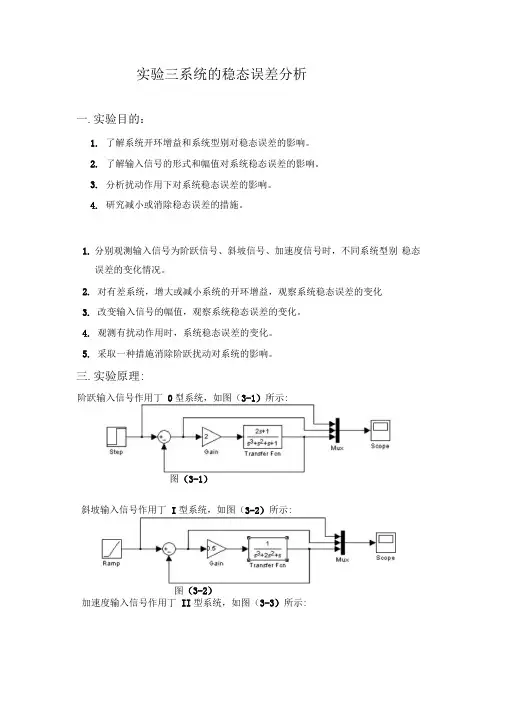
实验三系统的稳态误差分析一.实验目的:1.了解系统开环增益和系统型别对稳态误差的影响。
2.了解输入信号的形式和幅值对系统稳态误差的影响。
3.分析扰动作用下对系统稳态误差的影响。
4.研究减小或消除稳态误差的措施。
1.分别观测输入信号为阶跃信号、斜坡信号、加速度信号时,不同系统型别稳态误差的变化情况。
2.对有差系统,增大或减小系统的开环增益,观察系统稳态误差的变化3.改变输入信号的幅值,观察系统稳态误差的变化。
4.观测有扰动作用时,系统稳态误差的变化。
5.采取一种措施消除阶跃扰动对系统的影响。
三.实验原理:阶跃输入信号作用丁0型系统,如图(3-1)所示:图(3-1)斜坡输入信号作用丁I型系统,如图(3-2)所示:图(3-2)加速度输入信号作用丁II型系统,如图(3-3)所示:图(3-3)图(3-4)四.实验步骤:利用MATLAB中的Simulink仿真软件。
1.参照实验一的步骤,建立如图(3-1)所示的实验方块图进行仿真;2.单击工具栏中的卜图标,开始仿真,观测在阶跃输入信号作用下,型系统的输出曲线和误差曲线,记录此时的稳态误差值,并与理论计算值相比较;3.有误差时,调整“ Gain”模块的增益,观察稳态误差的变化,分析系统开环增益对稳态性能的影响;4.有误差时,调整输入信号的幅值,观察稳态误差的变化,分析输入信号的大小对稳态误差的影响;5.将对象分别更换为I型和皿型系统,观察在阶跃输入信号作用下,型和皿型系统的输出曲线和误差曲线,记录此时的稳态误差值。
6.更换输入信号的形式为斜坡信号,参考图(3-2)所示的实验方块图,重复步骤2~4,分别观测0型、I型和II型系统的稳态误差。
7.再将输入信号的形式更换为加速度信号,参考图(3-3)所示的实验方块图,重复步骤2~4,分别观测0型、I型和II型系统的稳态误差。
8.在扰动信号作用下,仿真实验方块图如图(3-4)所示,输入阶跃扰动信号,观测系统的输出曲线和误差曲线,记录此时的稳态误差值,并与计算的理论值相比较;9.调整“Gain”模块的增益,观察稳态误差有无变化;,10.再调整“Gainl”模块的增益,观察稳态误差有无变化;11.在扰动作用点之前增加积分环节消除阶跃扰动对系统输出的影响。

基于simulink汽车速度控制系统的设计与仿真摘要:目前许多汽车把汽车速度控制系统作为配属设备或选配设备。
汽车装有汽车速度控制系统后,当驾驶员启动这一装置并进行一些简单的设置后,该装置可自动保持某一恒定速度行驶,而不踩油门。
由于电子系统能准确地控制车辆的速度,从而使高速行驶的车辆更加安全、平稳。
在文中,首先对汽车的运动原理进行分析,建立控制系统简化模型,根据研究对象的物理特性建立起汽车速度控制控制系统的微分方程,再将该微分方程进行线性化处理,运用PID控制理论的方法对汽车速度控制控制系统进行分析和控制。
然后对汽车速度控制系统进行设计分析,在已有的模型下,对设计的汽车速度控制系统进行Matlab语言仿真。
关键词:速度控制系统PID控制仿真指导老师签名:Design and Simulation of the vehicle speedcontrol systemStudent name Class:Supervisor:Abstract:At present, many cars make car speed control system as an attachment device or optional equipment. The car is fitted with the motor speed control system, when the driver start the device and make some simple settings, the device can automatically maintain a constant speed, and do not step on the accelerator. Because the electronic system can accurately control the speed of the vehicle, so that the high-speed vehicles more secure, stable.In this paper, the first principle of the movement of automobile is analyzed, establishing control system is simplified model, based on physical characteristics of the research object to establish the vehicle speed control differential equation of the control system, then the differential equation is linearized by using the method of control theory, analyze and control the motor speed control system. Then the design of the vehicle speed control system, the existing model, to design vehicle speed control system simulation language Matlab.Keyword:Speed control system PID control simulationSignature of Supervisor:目录1绪论 (1)1.1选题的依据及课题意义 (1)1.2汽车速度控制研究概况及发展趋势 (1)2速度控制系统的简述 (3)2.1汽车速度控制系统原理 (3)2.2速度控制系统的分类 (3)2.3速度控制系统的基本用途 (4)2.4电子式多功能速度控制系统功能 (4)3系统模型建立及性能分析 (6)3.1汽车受力分析 (6)3.2行驶汽车仿真模型 (7)3.3 动态性能和稳态性能指标 (8)4 PID控制器 (10)4.1 PID控制简述 (10)4.2 PID控制规律 (10)4.3 PID作用分析 (14)5 系统仿真及结果分析 (15)5.1 SIMULINK简介 (15)5.2实验方案选择 (15)5.2.1采用P控制 (15)5.2.2采用PI控制 (20)5.2.3采用PID控制 (22)5.3实验结果分析 (25)总结 (26)参考文献 (27)致谢 (28)1绪论1.1选题的依据及课题意义随着汽车工业和公路运输业的发展,汽车将走进千家万户,驾驶人员非职业化的特点将突出,车辆驾驶的自动化己成为汽车发展的主要趋势。

simulink仿真实验报告Simulink仿真实验报告一、引言Simulink是一种基于模型的设计和仿真工具,广泛应用于各领域的工程设计和研究中。
本次实验将利用Simulink进行系统仿真实验,通过搭建模型、参数调整、仿真运行等过程,验证系统设计的正确性和有效性。
二、实验目的本实验旨在帮助学生掌握Simulink的基本使用方法,了解系统仿真的过程和注意事项。
通过本实验,学生将能够:1. 熟悉Simulink的界面和基本操作;2. 理解和掌握模型构建的基本原理和方法;3. 学会调整系统参数、运行仿真和分析仿真结果。
三、实验内容本实验分为以下几个步骤:1. 绘制系统模型:根据实验要求,利用Simulink绘制出所需的系统模型,包括输入、输出、控制器、传感器等。
2. 参数设置:针对所绘制的系统模型,根据实验要求设置系统的参数,例如增益、阻尼系数等。
3. 仿真运行:通过Simulink的仿真功能,对所构建的系统模型进行仿真运行。
4. 仿真结果分析:根据仿真结果,分析系统的动态性能、稳态性能等指标,并与理论值进行对比。
四、实验结果与分析根据实验要求,我们绘制了一个负反馈控制系统的模型,并设置了相应的参数。
通过Simulink的仿真功能,我们进行了仿真运行,并获得了仿真结果。
仿真结果显示,系统经过调整参数后,得到了较好的控制效果。
输出信号的稳态误差较小,并且在过渡过程中没有发生明显的振荡或超调现象。
通过与理论值进行对比,我们验证了系统的稳态稳定性和动态响应性能较为理想。
五、实验总结通过本次实验,我们掌握了使用Simulink进行系统仿真的基本方法和技巧。
了解了系统模型构建的基本原理,并学会了参数调整和仿真结果分析的方法。
这对于我们今后的工程设计和研究具有重要的意义。
六、参考文献1. 《Simulink使用手册》,XXX出版社,20XX年。
2. XXX,XXX,XXX等.《系统仿真与建模实践教程》. 北京:XXX出版社,20XX年。

自动控制系统的稳定性和稳态误差分析本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March实验三 自动控制系统的稳定性和稳态误差分析一、实验目的1、研究高阶系统的稳定性,验证稳定判据的正确性;2、了解系统增益变化对系统稳定性的影响;3、观察系统结构和稳态误差之间的关系。
二、实验任务1、稳定性分析欲判断系统的稳定性,只要求出系统的闭环极点即可,而系统的闭环极点就是闭环传递函数的分母多项式的根,可以利用MATLAB 中的tf2zp 函数求出系统的零极点,或者利用root 函数求分母多项式的根来确定系统的闭环极点,从而判断系统的稳定性。
(1)已知单位负反馈控制系统的开环传递函数为0.2( 2.5)()(0.5)(0.7)(3)s G s s s s s +=+++,用MATLAB 编写程序来判断闭环系统的稳定性,并绘制闭环系统的零极点图。
在MATLAB 命令窗口写入程序代码如下: z= p=[0,,,-3] k=Go=zpk(z,p,k) Gc=feedback(Go,1) Gctf=tf(Gc) 运行结果如下: Transfer function: s +--------------------------------------- s^4 + s^3 + s^2 + s +s^4 + s^3 + s^2 + s + 是系统的特征多项式,接着输入如下MATLAB程序代码:den=[1,,,,]p=roots(den)运行结果如下:p =+-p为特征多项式dens的根,即为系统的闭环极点,所有闭环极点都是负的实部,因此闭环系统是稳定的。
下面绘制系统的零极点图,MATLAB程序代码如下:z=p=[0,,,-3]k=Go=zpk(z,p,k)Gc=feedback(Go,1)Gctf=tf(Gc)[z,p,k]=zpkdata(Gctf,'v')pzmap(Gctf)grid运行结果如下:z =p =+-k =输出零极点分布图如图3-1所示。

实验三 自动控制系统的稳定性和稳态误差分析一、实验目的1、研究高阶系统的稳定性,验证稳定判据的正确性;2、了解系统增益变化对系统稳定性的影响;3、观察系统结构和稳态误差之间的关系。
二、实验任务1、稳定性分析欲判断系统的稳定性,只要求出系统的闭环极点即可,而系统的闭环极点就是闭环传递函数的分母多项式的根,可以利用MATLAB 中的tf2zp 函数求出系统的零极点,或者利用root 函数求分母多项式的根来确定系统的闭环极点,从而判断系统的稳定性。
(1)已知单位负反馈控制系统的开环传递函数为0.2( 2.5)()(0.5)(0.7)(3)s G s s s s s +=+++,用MATLAB 编写程序来判断闭环系统的稳定性,并绘制闭环系统的零极点图。
在MATLAB 命令窗口写入程序代码如下: z=-2.5p=[0,-0.5,-0.7,-3] k=0.2 Go=zpk(z,p,k) Gc=feedback(Go,1) Gctf=tf(Gc) 运行结果如下: Transfer function: 0.2 s + 0.5 --------------------------------------- s^4 + 4.2 s^3 + 3.95 s^2 + 1.25 s + 0.5s^4 + 4.2 s^3 + 3.95 s^2 + 1.25 s + 0.5是系统的特征多项式,接着输入如下MATLAB程序代码:den=[1,4.2,3.95,1.25,0.5]p=roots(den)运行结果如下:p =-3.0058-1.0000-0.0971 + 0.3961i-0.0971 - 0.3961ip为特征多项式dens的根,即为系统的闭环极点,所有闭环极点都是负的实部,因此闭环系统是稳定的。
下面绘制系统的零极点图,MATLAB程序代码如下:z=-2.5p=[0,-0.5,-0.7,-3]k=0.2Go=zpk(z,p,k)Gc=feedback(Go,1)Gctf=tf(Gc)[z,p,k]=zpkdata(Gctf,'v')pzmap(Gctf)grid运行结果如下:z =-2.5000p =-3.0058-1.0000-0.0971 + 0.3961i-0.0971 - 0.3961ik =0.2000输出零极点分布图如图3-1所示。

自动控制技术与其应用实验报告系别:班级:XX:学号:实验二典型环节与其阶跃响应(▲)一、实验目的1. 学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2. 学习典型环节阶跃响应的测量方法,并学会由阶跃响应曲线计算典型环节的传递函数。
3. 学习用MATLAB仿真软件对实验内容中的电路进行仿真。
二、实验设备和仪器1.计算机;2. MA TLAB软件三、实验结果分析与结论1.比例环节 G1(S)=1和G2(S)=2(二选一)比例环节仿真仿真结构图单位阶跃响应波形图比例环节特点:成比例,无失真和延迟2.惯性环节 G1(S)=1/(S+1)和G2(S)=1/(0.5S+1) (二选一)绘制:仿真结构图、单位阶跃响应波形图(需要注明必要的特殊点)惯性环节仿真仿真结构图单位阶跃响应波形图惯性环节特点:输出量不能立即随输入量的变化而变化,存在时间上延迟,输出无振荡3.积分环节G1(S)=(1/S)和G2(S)=(1/(0.5S))绘制:仿真结构图、单位阶跃响应波形图(需要注明必要的特殊点)积分环节仿真仿真结构图单位阶跃响应波形图积分环节仿真仿真结构图单位阶跃响应波形图积分环节特点:输出量反应输入量的时间积累4.微分环节G1(S)=0.5S和G2(S)=2S绘制:仿真结构图、单位阶跃响应波形图(需要注明必要的特殊点)微分环节仿真仿真结构图单位阶跃响应波形图微分环节仿真仿真结构图单位阶跃响应波形图微分环节特点:输出能够预示输入信号的变化趋势5.比例微分环节G1(S)=(2+S)和G2(S)=(1+2S)绘制:仿真结构图、单位阶跃响应波形图(需要注明必要的特殊点)比例微分环节仿真仿真结构图单位阶跃响应波形图比例微分环节仿真仿真结构图单位阶跃响应波形图比例微分环节特点:调节与时,偏差小,当输出稳定时的幅值与比例环节的比例系数成正比6.比例积分环节G1(S)=(1+1/S)和G2(S)=2(1+1/2S)绘制:仿真结构图、单位阶跃响应波形图(需要注明必要的特殊点)比例积分环节仿真仿真结构图单位阶跃响应波形图比例积分环节仿真仿真结构图单位阶跃响应波形图比例积分环节特点:应速度变快,其输出与积分时间常数有关四、实验心得与体会通过实验可以更加形象生动、清晰、一目了然,让我们更容易掌握各个环节的特点,同时掌握了MATLAB 的一些基本绘图仿真知识。

MATLAB/Simulink与控制系统仿真实验报告姓名:喻彬彬学号:K031541725实验1、MATLAB/Simulink 仿真基础及控制系统模型的建立一、实验目的1、掌握MATLAB/Simulink 仿真的基本知识;2、熟练应用MATLAB 软件建立控制系统模型。
二、实验设备电脑一台;MATLAB 仿真软件一个三、实验内容1、熟悉MATLAB/Smulink 仿真软件。
2、一个单位负反馈二阶系统,其开环传递函数为210()3G s s s =+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
3、某控制系统的传递函数为()()()1()Y s G s X s G s =+,其中250()23s G s s s+=+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
4、一闭环系统结构如图所示,其中系统前向通道的传递函数为320.520()0.11220s G s s s s s+=+++,而且前向通道有一个[-0.2,0.5]的限幅环节,图中用N 表示,反馈通道的增益为1.5,系统为负反馈,阶跃输入经1.5倍的增益作用到系统。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
四、实验报告要求实验报告撰写应包括实验名称、实验内容、实验要求、实验步骤、实验结果及分析和实验体会。
五、实验思考题总结仿真模型构建及调试过程中的心得体会。
题1、(1)利用Simulink的Library窗口中的【File】→【New】,打开一个新的模型窗口。
(2)分别从信号源库(Sourse)、输出方式库(Sink)、数学运算库(Math)、连续系统库(Continuous)中,用鼠标把阶跃信号发生器(Step)、示波器(Scope)、传递函数(Transfern Fcn)和相加器(Sum)4个标准功能模块选中,并将其拖至模型窗口。

河南机电高等专科学校《自动控制原理》实验指导书专业:电气自动化技术、计算机控制技术生产过程自动化技术等吴君晓编2008年9月目录实验一 (2)实验二 (4)实验三 (6)实验四 (8)实验五 (10)实验六 (12)实验七 (14)实验八 (15)实验九 (17)实验一建立MATLAB环境下控制系统数学模型一. 实验目的1.熟悉MATLAB实验环境,掌握MATLAB命令窗口的基本操作。
2.掌握MATLAB建立控制系统数学模型的命令及模型相互转换的方法。
3.掌握使用MATLAB命令化简模型基本连接的方法。
二、实验设备和仪器1.计算机2. MATLAB软件三、实验原理控制系统常用的数学模型有四种:传递函数模型(tf对象)、零极点增益模型(zpk对象)、结构框图模型和状态空间模型(ss对象)。
经典控制理论中数学模型一般使用前三种模型,状态空间模型属于现代控制理论范畴。
1.传递函数模型(也称为多项式模型)连续系统的传递函数模型为:在MATLAB中用分子、分母多项式系数按s的降幂次序构成两个向量:num = [ b0 , b1 ,…, bm ] ,den = [ a0 , a1 ,…, an]。
用函数tf ( )来建立控制系统的传递函数模型,其命令调用格式为:G = tf ( num , den )注意:对于已知的多项式模型传递函数,其分子、分母多项式系数两个向量可分别用G.num{1}与G.den{1}命令求出。
2.零极点增益模型零极点模型是是分别对原传递函数的分子、分母进行因式分解,以获得系统的零点和极点的表示形式。
式中,K为系统增益,z1,z2,…,z m为系统零点,p1,p2,…,p n为系统极点。
在MATLAB 中,用向量z,p,k构成矢量组[ z, p, k ]表示系统。
即z = [ z1, z2 ,…,z m ],p = [ p1, p2,…, p n ],k = [ k ],用函数命令zpk ( )来建立系统的零极点增益模型,其函数调用格式为:G = zpk ( z, p, k )3.控制系统模型间的相互转换零极点模型转换为多项式模型: G=zpk(G)多项式模型转化为零极点模型: G=tf(G)4.系统反馈连接之后的等效传递函数两个环节反馈连接后,其等效传递函数可用feedback ( )函数求得。

simulink仿真实验报告Simulink 仿真实验报告引言:Simulink 是一种常用的建模和仿真工具,它可以帮助工程师们在设计和开发过程中进行系统级建模和仿真。
本文将通过一个实际的仿真实验来展示 Simulink 的应用。
一、实验背景在现代工程领域中,系统的建模和仿真是非常重要的一步。
通过仿真实验,我们可以在实际制造之前对系统进行测试和优化,节省了时间和成本。
本实验的目标是使用 Simulink 对一个电机驱动系统进行建模和仿真,以验证其性能和稳定性。
二、实验步骤1. 系统建模在 Simulink 中,我们首先需要将电机驱动系统进行建模。
我们可以使用Simulink 提供的各种组件来构建系统模型,例如传感器、控制器、电机等。
在本实验中,我们将使用 PID 控制器来控制电机的转速。
2. 参数设置在建模过程中,我们需要设置各个组件的参数。
例如,我们需要设置 PID 控制器的比例、积分和微分系数,以及电机的转动惯量和阻尼系数等。
这些参数的设置将直接影响系统的性能。
3. 仿真运行在模型建立和参数设置完成后,我们可以进行仿真运行。
通过设置仿真时间和输入信号,我们可以观察系统在不同条件下的响应情况。
例如,我们可以通过改变输入信号的频率和幅度来测试系统的稳定性和鲁棒性。
4. 结果分析仿真运行完成后,我们可以分析仿真结果。
通过观察输出信号的波形和频谱,我们可以评估系统的性能和稳定性。
例如,我们可以计算系统的响应时间、超调量和稳态误差等指标,以评估系统的控制效果。
三、实验结果在本实验中,我们成功建立了一个电机驱动系统的 Simulink 模型,并进行了仿真运行。
通过观察仿真结果,我们发现系统在不同输入信号条件下的响应情况。
在一些情况下,系统的响应时间较短,稳态误差较小,表现出良好的控制效果。
然而,在一些极端情况下,系统可能出现超调或不稳定的现象,需要进一步优化参数和控制策略。
四、实验总结通过本次仿真实验,我们深入了解了 Simulink 的应用和优势。
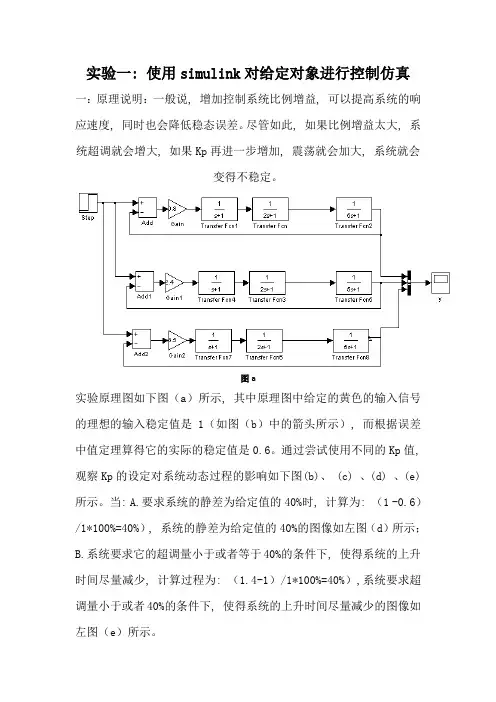
实验一: 使用simulink对给定对象进行控制仿真一:原理说明:一般说, 增加控制系统比例增益, 可以提高系统的响应速度, 同时也会降低稳态误差。
尽管如此, 如果比例增益太大, 系统超调就会增大, 如果Kp再进一步增加, 震荡就会加大, 系统就会变得不稳定。
图a实验原理图如下图(a)所示, 其中原理图中给定的黄色的输入信号的理想的输入稳定值是1(如图(b)中的箭头所示), 而根据误差中值定理算得它的实际的稳定值是0.6。
通过尝试使用不同的Kp值, 观察Kp的设定对系统动态过程的影响如下图(b)、 (c) 、(d) 、(e)所示。
当: A.要求系统的静差为给定值的40%时, 计算为: (1 -0.6)/1*100%=40%), 系统的静差为给定值的40%的图像如左图(d)所示;B.系统要求它的超调量小于或者等于40%的条件下, 使得系统的上升时间尽量减少, 计算过程为: (1.4-1)/1*100%=40%),系统要求超调量小于或者40%的条件下, 使得系统的上升时间尽量减少的图像如左图(e)所示。
一: 当给定KP 分别为 0.8、2.4、3.5 :Kp 的设定对系统动态过程的影响图像如左图(b )所示:1_1: 当调节KP 分别为1.3.5:Kp 的设定对系统动态过程的影响图像如左图(c )所示:1_2: 当调节KP 分别为 1.5.3.5 : 图(b )图(c )系统的静差为给定值40%(注: (1-0.6)/1*100%=40%)的图像如左图(d)所示:图(d)对于单位负反馈, 静差E(S)=R(S)-C(S), 其中输入信号为1(t)根据终值定理可知当KP取1.5时, 系统的静差刚好为给定值的40%。
1_3: 当调节KP分别为7、3.5:➢系统要超调量小于或40%((1.4-1)/1*100%=40%)条件下, 使系统上升时间尽量减少如图(e)所示:➢总结: 联系上图(b)、(c)、(d)、(e)可知, KP由0.8一直增大到7可以看出, 增大比例系数KP可以加快系统的响应, 在有静差的时候有助于减小静差。
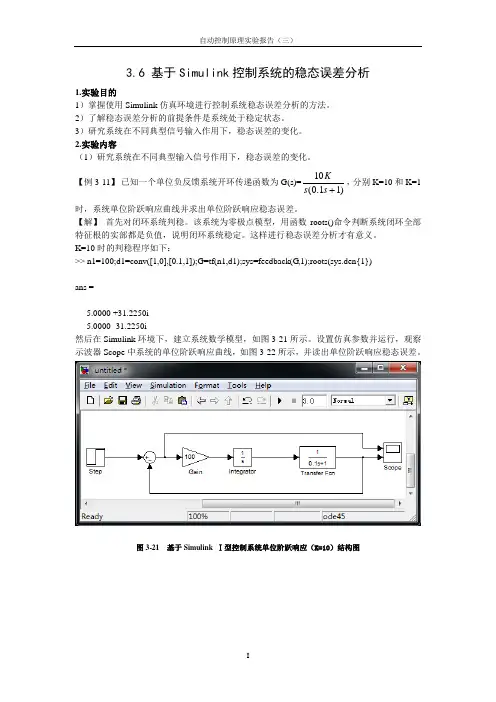
3.6 基于Simulink 控制系统的稳态误差分析1.实验目的1)掌握使用Simulink 仿真环境进行控制系统稳态误差分析的方法。
2)了解稳态误差分析的前提条件是系统处于稳定状态。
3)研究系统在不同典型信号输入作用下,稳态误差的变化。
2.实验内容(1)研究系统在不同典型输入信号作用下,稳态误差的变化。
【例3-11】 已知一个单位负反馈系统开环传递函数为G(s)=)11.0(10 s s K ,分别K=10和K=1时,系统单位阶跃响应曲线并求出单位阶跃响应稳态误差。
【解】 首先对闭环系统判稳。
该系统为零极点模型,用函数roots()命令判断系统闭环全部特征根的实部都是负值,说明闭环系统稳定。
这样进行稳态误差分析才有意义。
K=10时的判稳程序如下:>> n1=100;d1=conv([1,0],[0.1,1]);G=tf(n1,d1);sys=feedback(G ,1);roots(sys.den{1})ans =-5.0000 +31.2250i-5.0000 -31.2250i然后在Simulink 环境下,建立系统数学模型,如图3-21所示。
设置仿真参数并运行,观察示波器Scope 中系统的单位阶跃响应曲线,如图3-22所示,并读出单位阶跃响应稳态误差。
图3-21 基于Simulink Ⅰ型控制系统单位阶跃响应(K=10)结构图图3-22 基于Simulink Ⅰ型控制系统单位阶跃响应稳态误差曲线【分析】实验曲线表明,Ⅰ型单位反馈系统在单位阶跃输入作用下,稳态误差e ssr=0,即Ⅰ型单位反馈系统稳态时能完全跟踪阶跃输入,是一阶无静差系统。
K=1时的判稳程序如下:>> n1=10;d1=conv([1,0],[0.1,1]);G=tf(n1,d1);sys=feedback(G,1);roots(sys.den{1})ans =-5.0000 + 8.6603i-5.0000 - 8.6603i在Simulink环境下建立的数学模型及仿真参数运行后示波器Scope中系统的单位阶跃响应曲线如下图所示。
电子科技大学中山学院学生实验报告学院:机电工程学院专业:17自动化课程名称:自动控制原理实验与仿真成绩:批改时间:一、实验目的(1)掌握使用Simulink仿真环境进行控制系统稳态误差分析的方法。
(2)了解稳态误差分析的前提条件是系统处于稳定状态。
(3)研究系统在不同典型输入信号作用下,稳态误差的变化。
(4)分析系统在扰动输入作用下的稳态误差。
(5)分析系统型别及开环增益对稳态误差的影响。
二、实验条件实验设备:每人一台计算机奔腾系列以上计算机,配置硬盘≥2G,内存≥64M。
实验软件:WINDOWS操作系统(WINDOWS XP 或WINDOWS 2000),并安装MATLAB语言编程环境。
三、实验内容(1)研究系统在不同典型输入信号作用下,稳态误差的变化。
【1】已知一个单位负反馈系统开环传递函数为10()(0.11)KG ss s=+分别作出K=1和K=10时,系统单位阶跃响应曲线并求单位阶跃响应稳态误差。
模型:结论:系统型次越高,系统对斜坡输入的稳态误差越小,故可以通过提高系统的型次达到降低稳态误差的效果。
(3)分析系统在扰动输入作用下的稳态误差。
【5】已知系统,若输入信号 r ( t ) = 1 ( t ) ,扰动信号 n (t) =0.1 * 1 ( t ) ,令 e ( t ) =r (t) – c (t) ,求系统总的稳态误差。
曲线:结论:系统的总稳态误差ess=essr+essn=-0.1 100.1s+1Transfer Fcn2Transfer Fcn1Transfer FcnStep1StepScope1ScopeRamp 1s Integrator1Gain1Gain可见,扰动点前移至反馈比较点之后,系统的稳态误差为零。
4)由于simulink环境中的模块组中,没有加速度信号源,如何实现加速度信号的输入仿真?在matlab设计程序,完成输入信号为加速度信号的控制系统仿真。
答:在斜坡信号后再加一个积分环节。
MATLAB/Simulink 与控制系统仿真实验报告姓名:喻彬彬学号:K031541725实验1、MATLAB/Simulink 仿真基础及控制系统模型的建立一、实验目的1、掌握MATLAB/Simulink 仿真的基本知识;2、熟练应用MATLAB 软件建立控制系统模型。
二、实验设备电脑一台;MATLAB 仿真软件一个三、实验内容1、熟悉MATLAB/Smulink 仿真软件。
2、一个单位负反馈二阶系统,其开环传递函数为210()3G s s s =+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
3、某控制系统的传递函数为()()()1()Y s G s X s G s =+,其中250()23s G s s s+=+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
4、一闭环系统结构如图所示,其中系统前向通道的传递函数为320.520()0.11220s G s s s s s+=+++g ,而且前向通道有一个[-0.2,0.5]的限幅环节,图中用N 表示,反馈通道的增益为1.5,系统为负反馈,阶跃输入经1.5倍的增益作用到系统。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
四、实验报告要求实验报告撰写应包括实验名称、实验内容、实验要求、实验步骤、实验结果及分析和实验体会。
五、实验思考题总结仿真模型构建及调试过程中的心得体会。
题1、(1)利用Simulink的Library窗口中的【File】→【New】,打开一个新的模型窗口。
(2)分别从信号源库(Sourse)、输出方式库(Sink)、数学运算库(Math)、连续系统库(Continuous)中,用鼠标把阶跃信号发生器(Step)、示波器(Scope)、传递函数(Transfern Fcn)和相加器(Sum)4个标准功能模块选中,并将其拖至模型窗口。
利用Simulink搭建PID控制系统模型及分析——201706527曾庆松在参考了《过程控制系统》一书中PID调节原理相关章节的基础上,利用Matlab的Simulink仿真器搭建PID控制系统模型,并进行仿真,对PID控制器的三个参数Kp,Ki,Kd与控制性能(稳态误差,上升时间,峰值时间,调节时间,超调量等)之间的关系进行分析,其完整过程如下。
一、搭建模型搭建好的PID控制系统模型如图1所示,其中输入为阶跃响应,被控对象为二阶惯性环节。
其输出响应曲线如图2所示。
图 1 PID控制系统模型图2系统输出响应曲线二、参数对性能影响的分析1、Kp的影响。
图 3 调整Kp时输出响应曲线的变化从图中可以看出对于一个已经设计好的PID控制器,当Kp的值变小时系统的峰值时间、上升时间变长,超调量增加,甚至造成系统不稳定;而当Kp的值变大时则会造成系统震荡加剧。
2、Ki的影响。
图 4 调整Ki时输出响应曲线的变化从曲线的变化情况可以看出,当Ki的值变大时将导致系统产生减幅震荡,Ki过小时又会使系统的稳态误差增大。
3、Kd的影响。
图 5 调整Kd时输出响应曲线的变化从输出响应曲线的变化情况来看,当Kd的值减小时系统的超调量明显增加,调节时间、上升时间等参数也受到影响;当Kd的值增加时系统的调节时间大大增加,并且稳态误差较大,系统反应速度满且调节效果很差。
三、总结1、比例增益Kp的作用比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
增大Kp就等于加大系统的开环增益,结果导致系统剧烈震荡甚至不稳定。
2、积分时间Ki的作用在积分控制中,控制器的输出与输入误差信号的积分成正比关系,所以主要用于消除静差,提高系统的无差度。
增大Ki将造成系统稳定性下降,直到出现发散的震荡过程。
3、微分时间Kd的作用在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
所以微分控制可以减小超调量,克服振荡,使系统的稳定性提高,同时加快系统的动态响应速度,减小调节时间,从而改善系统的动态性能。
实验六 系统稳态误差例1 已知单位负反馈控制系统,其中开环传递函数为25()(10)s G s s s +=+,试计算当输入分别为单位阶跃信号、单位斜坡信号和单位加速度信号时系统的稳态误差。
步骤如下:① 输入信号为单位阶跃信号,在simulink 中建立如下模型,示波器参数中的stop time设置为300。
图一 单位阶跃输入系统模型及稳态误差曲线② 输入信号为单位斜坡信号,在simulink 中建立如下模型,示波器参数中的stop time设置为300。
图二 单位斜坡输入系统模型及响应曲线图三 稳态误差曲线③单位加速度信号有单位斜坡信号和20.5y u (u 为输入信号,y 为输出信号)的函数串联而成。
操作方法:③双击Fcn,跳出对话框,在“Expression”中输入“0.5*u^2”,如下图所示。
图三 单位加速度输入系统模型及稳态误差曲线结论:系统是II 型系统,因此在阶跃、斜坡输入信号下,系统的稳态误差都为零,在加速度信号输入下,存在稳态误差,通过放大示波器可准确看到数值为2。
实验要求:一、对于开环传递函数G (s )=)5(25s s ,①在simulink 中分别求其单位阶跃、单位斜波和单位加速度单位负反馈响应曲线,并计算出其稳态误差。
截图存档。
②在simulink 中利用加法器add 获取输入为r (t )=1+2t 时单位负反馈响应曲线,并计算稳态误差。
截图存档。
③在simulink中利用加法器add获取输入r(t)=1+2t+0.5t^2时单位负反馈响应曲线,并计算稳态误差,截图存档。
自动控制原理上机实验指导书王芳、杨志超编写南京工程学院电力工程学院二〇〇七年二月目录Simulink仿真集成环境简介 (2)实验一典型环节的性能分析 (11)实验二二阶系统的性能分析 (14)实验三自动控制系统的稳定性和稳态误差分析 (17)实验四自动控制系统根轨迹的分析 (22)实验五自动控制系统的频域分析 (27)实验六控制系统的校正及设计 (32)实验七非线性系统的稳定性分析 (39)Simulink仿真集成环境简介Simulink是可视化动态系统仿真环境。
1990年正式由Mathworks公司引入到MATLAB中,它是Slmutation 和Link的结合。
这里主要介绍它的使用方法和它在控制系统仿真分析和设计操作的有关内容。
1、进入Simulink操作环境双击桌面上的MATLAB图标,启动MATLAB,进入开发环境,如图0-1所示:图0-1 MATLAB开发环境从MATLAB的桌面操作环境画面进入Simulink操作环境有多种方法,介绍如下:①点击工具栏的Simulink图标,弹出如图0-2的图形库浏览器画面。
②在命令窗口键入“simulink”命令,可自动弹出图形库浏览器。
上述两种方法需从该画面“File”下拉式菜单中选择“New/Model”,或点击图标,得到图0-3的图形仿真操作画面。
③从“File”下拉式菜单中选择“New/Model”,弹出图0-3所示的未命名的图形仿真操作画面。
从工具栏中点击图形库浏览器图标,调出图0-2的图形库浏览器画面。
图0-3用于仿真操作,图0-2的图形库用于提取仿真所需的功能模块。
图0-2 Simulink图形库浏览器画面图0-3 simulink仿真操作环境画面2、提取所需的仿真模块在提取所需仿真模块前,应绘制仿真系统框图,并确定仿真所用的参数。
图0-2中的仿真用图形库,提供了所需的基本功能模块,能满足系统仿真的需要。
该图形库有多种图形子库,用于配合有关的工具箱。
基于Simulink 控制系统的稳态误差分析
一、实验目的
1.掌握使用Simulink 仿真环境进行控制系统稳态误差分析的方法。
2.了解稳态误差分析的前提条件是系统处于稳定状态。
3.研究系统在不同典型输入信号作用下,稳态误差的变化。
4.分析系统在扰动输入作用下的稳态误差。
5.分析系统型次及开环增益对稳态误差的影响。
二、实验设备和仪器
1.计算机
2. MATLAB 软件
三、实验原理
1.误差的意义: a) 给定信号作用下的稳
态误差表征系统输出跟随输入信号的能力。
b) 系统经常处于各种扰动作用下。
如:负载力矩的变化,电源电压和频率的波动,环境温度的变化等。
因此系统在扰动作用下的稳态误差数值,反映了系统的抗干扰能力。
注意:系统只有在稳定的前提下,才能对稳态误差进行分析。
定义式法求稳态误差:
2. 给定信号作用下的误差
E 扰动信号作用下的误差()d E s R(s)是给定输入信号(简称给定信号)
;D(s)是扰动输入信号(简称扰动信号);()()G s H s 是开环传递函数。
3. 静态误差系数法(只能用于求给定信号作用下误差)
这种简便的求解给定信号稳态误差
ssr e 的方法叫做静态误差系数法,首先给出系统在不同输入信号下的误差系数的定义:
当()0R
R s s
=时,定义静态位置误差
系数为:0
lim ()()p s K G s H s →=
当()0
2v R s s =
时,定义静态速度误差系数为:0lim ()()v s K s G s H s →=g 当()0
3a R s s
=时,定义静态加速度误差系数为:20lim (
)()a s K s G s H s →=g 表5-1 给定信号作用下系统稳态误差e
R
1.对比“给定信号作用下系统稳态误差ssr e 表”分析发现,影响系统稳态误差ssr e 有以下2个方面:
a) 系统的结构参数 b) 输入信号
2.分析系统在给定输入作用下的稳态误差,验证上面的结论。
构建如下图所示的2个稳定的单位负反馈系统,仿真运行后,将实验结果填入下表:
图5-1 实验对象Simulink 连接图 表5-2 图5-1给定信号作用下系统
Step Response
Time (sec)
A m p l i t u d e
0型系统单位斜坡 1型系统单位斜坡 单位阶跃的1型
构建如下图所示的单位负反馈系统,若输入信号()1()r t t = ,扰动信号
()0.11()n t t =•,仿真运行后,得到给定信号作用下稳态误差ssr e = 0 ,
扰动信号作用下稳态误差ssn e = -0.1 ,总的稳态误差ss ssr ssn e e e =+= -0.1 。
五、实验心得与体会
通过本次试验,我学会了怎样用Simulink 进行仿真实验,并能够通过简单的仿真对影响系统稳态误差的因素进行分析。
在不同的输入信号下,系统的稳态误差也有不同的变化,通过对系统的分析,可以通过改变因素来使系统达到稳定。