递延年金终值和现值
- 格式:doc
- 大小:56.50 KB
- 文档页数:4

2020年中级会计职称考试《财务管理》考点精讲第二节财务管理基础【考情分析】本章是重点章,主要介绍货币时间价值、风险与收益以及成本性态等内容,是预算管理、筹资管理、投资管理、成本管理等后续章节的先导知识。
本章题型比较全面,其中,货币时间价值中的现值计算可以与项目投资管理、证券投资管理等结合考计算分析题或综合题,也可以单独考计算分析题(如2018年度考题)。
风险与收益中的资本资产定价模型可以同普通股资本成本的计算、普通股价值评估等结合考计算分析题或综合题。
本章各年分值波动幅度较大,预计2020年分值在8分左右。
本章近三年题型、分值分布【主要考点】1.货币时间价值的计算(1)复利终现值与年金终现值的计算(2)利率的推算①利用插值法推算利率②名义利率与实际利率的换算2.风险与收益(1)资产收益率的构成与类型(2)风险的含义(3)风险对策(4)风险矩阵(5)风险管理原则(6)单项资产与资产组合的风险与收益衡量(7)系统风险与资本资产定价模型3.成本性态分析(1)成本按性态的分类:固定成本、变动成本、混合成本(2)混合成本的分解方法第一节货币时间价值知识点:货币时间价值的概念1.货币时间价值是指没有风险和没有通货膨胀情况下,货币经历一定时间的投资和再投资所增加的价值。
(1)货币进行投资才会产生价值增值。
(2)货币时间价值(纯粹利率)是投资收益率的基础,在有风险和通货膨胀的情况下,投资者会要求获得更高的投资收益率,即:投资收益率=货币时间价值+通货膨胀补贴+风险收益率 在没有风险和通货膨胀的情况下,有: 投资收益率=货币时间价值2.投资收益率的存在,使货币随着时间的推移产生价值增值,从而使不同时点的单位货币具有不同的价值量。
一般来说,发生时间越早的单位货币,其价值量越大。
【示例】今天的1块钱比明年的1块钱更值钱。
3.货币时间价值计算实质上是以投资收益率为依据,将货币的价值量在不同时点之间进行换算。
(1)由于不同时点的单位货币具有不同的价值量,因此,不同时点的货币不能直接进行比较,必须换算到相同时点上,才能进行比较。


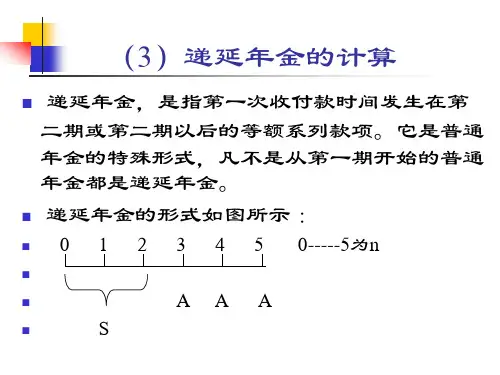
财务管理》第二章重难点讲解及例题:递延年金终值和现值递延年金终值和现值(1)递延年金终值(已知从第二期或第二期以后等额收付的普通年金A,求FA)递延年金是指第-次等额收付发生在第二期或第二期以后的普通年金。
图示如下:求递延年金的终值与求普通年金的终值没有差别(要注意期数),递延年金终值与递延期无关。
如上图中,递延年金的终值为:FA=AX(F/A,i,n),其中,“n,,表示的是A的个数,与递延期无关。
(2)递延年金现值(已知从第二期或第二期以后等额收付的普通年金A,求PA)方法-:把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第-次等额收付前-期的数值,再往前推递延期期数就得出递延年金的现值。
图示如下:PA=AX(P/A,i,n)×(P/F,i,m)方法二:把递延期每期期末都当作有等额的收付,把递延期和以后各期看成是-个普通年金,计算这个普通年金的现值,再把递延期多算的年金现值减去即可。
图示如下:PA=AX(P/A,i,m+n)-A×(P/A,i,m)【提示】方法-、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题,再求递延年金现值。
方法三:先求递延年金的终值,再将终值换算成现值,图示如下:PA=A×(F/A,i,n)×(P/F,i,m+n)【提示】递延年金现值计算公式中的“n”指的是等额收付的次数,即A的个数;递延期“m”的含义是,把普通年金(第-次等额收付发生在第1期期末)递延m期之后,就变成了递延年金(第-次等额收付发生在第W期期末,W>1)。
因此,可以按照下面的简便方法确定递延期m的数值:(1)确定该递延年金的第-次收付发生在第几期末(假设为第W期末)(此时应该注意“下-期的期初相当于上-期的期末”);(2)根据(W-1)的数值确定递延期m的数值。
【例题7.单选题】下列关于递延年金的说法中,错误的是()。
A.递延年金是指隔若干期以后才开始发生的系列等额收付款项B.递延年金没有终值C.递延年金现值的大小与递延期有关,递延期越长,现值越小D.递延年金终值与递延期无关【答案】B【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项;递延年金存在终值,其终值的计算与普通年金是相同的;终值的大小与递延期无关;但是递延年金的现值与递延期是有关的,递延期越长,递延年金的现值越小,所以选项B的说法是错误的。

财务管理》第二章重难点讲解及例题:递延年金终值和现值递延年金终值和现值(1)递延年金终值(已知从第二期或第二期以后等额收付的普通年金A,求FA)递延年金是指第-次等额收付发生在第二期或第二期以后的普通年金。
图示如下:求递延年金的终值与求普通年金的终值没有差别(要注意期数),递延年金终值与递延期无关。
如上图中,递延年金的终值为:FA=AX(F/A,i,n),其中,“n,,表示的是A的个数,与递延期无关。
(2)递延年金现值(已知从第二期或第二期以后等额收付的普通年金A,求PA)方法-:把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第-次等额收付前-期的数值,再往前推递延期期数就得出递延年金的现值。
图示如下:PA=AX(P/A,i,n)×(P/F,i,m)方法二:把递延期每期期末都当作有等额的收付,把递延期和以后各期看成是-个普通年金,计算这个普通年金的现值,再把递延期多算的年金现值减去即可。
图示如下:PA=AX(P/A,i,m+n)-A×(P/A,i,m)【提示】方法-、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题,再求递延年金现值。
方法三:先求递延年金的终值,再将终值换算成现值,图示如下:PA=A×(F/A,i,n)×(P/F,i,m+n)【提示】递延年金现值计算公式中的“n”指的是等额收付的次数,即A的个数;递延期“m”的含义是,把普通年金(第-次等额收付发生在第1期期末)递延m期之后,就变成了递延年金(第-次等额收付发生在第W期期末,W>1)。
因此,可以按照下面的简便方法确定递延期m的数值:(1)确定该递延年金的第-次收付发生在第几期末(假设为第W期末)(此时应该注意“下-期的期初相当于上-期的期末”);(2)根据(W-1)的数值确定递延期m的数值。
【例题7.单选题】下列关于递延年金的说法中,错误的是()。
A.递延年金是指隔若干期以后才开始发生的系列等额收付款项B.递延年金没有终值C.递延年金现值的大小与递延期有关,递延期越长,现值越小D.递延年金终值与递延期无关【答案】B【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项;递延年金存在终值,其终值的计算与普通年金是相同的;终值的大小与递延期无关;但是递延年金的现值与递延期是有关的,递延期越长,递延年金的现值越小,所以选项B的说法是错误的。

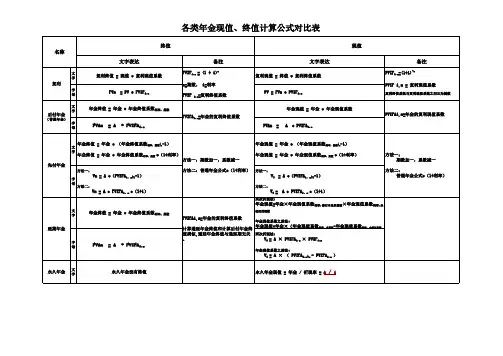
六、年金终值和年金现值的计算(一)年金的含义年金是指一定时期内每次等额收付的系列款项。
通常记作A 。
具有两个特点:一是金额相等;二是时间间隔相等。
也可以理解为年金是指等额、定期的系列收支。
在现实工作中年金应用很广泛。
例如,分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款、每年相同的销售收入等,都属于年金收付形式。
老师手写板:①②年、月、半年、2年1年 2年 3年1年 1年 1年(二)年金的种类年金按其每次收付款项发生的时点不同,可以分为四种:普通年金(后付年金):从第一期开始每期期末收款、付款的年金。
预付年金(先付年金、即付年金):从第一期开始每期期初收款、付款的年金。
与普通年金的区别仅在于付款时间的不同。
递延年金:从第二期或第二期以后开始每期期末收付的年金。
永续年金:无限期的普通年金。
注意:各种类型年金之间的关系(1)普通年金和即付年金区别:普通年金的款项收付发生在每期期末,即付年金的款项收付发生在每期期初。
联系:第一期均出现款项收付。
【例题1·单选题】2007年1月1日,甲公司租用一层写字楼作为办公场所,租赁期限3年,每年12月31日支付租金10万元,共支付3年。
该租金有年金的特点,属于( )。
(2010年考试真题)A .普通年金B .即付年金C .递延年金D .永续年金【答案】A【解析】每年年末发生等额年金的是普通年金。
(2)递延年金和永续年金二者都是在普通年金的基础上发展演变起来的,它们都是普通年金的特殊形式。
它们与普通年金的共同点有:它们都是每期期末发生的。
区别在于递延年金前面有一个递延期,也就是前面几期没有现金流,永续年金没有终点。
在年金的四种类型中,最基本的是普通年金,其他类型的年金都可以看成是普通年金的转化形式。
【提示】1.这里的年金收付间隔的时间不一定是1年,可以是半年、一个季度或者一个月等。
A A A A A A A A A A 300万 200万 100万2.这里年金收付的起止时间可以是从任何时点开始,如一年的间隔期,不一定是从1月1日至12月31日,可以是从当年7月1日至次年6月30日。

解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21Λ 式中的分式ii n -+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式是先计算出n 期的普通年金现值,然后减去前s 期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。



递延年金的终值和现值递延年金是指一种投资工具或保险产品,在某一指定时间期限内,投资者或保险人按一定的金额或比例定期缴纳保费或投资款项,直到特定日期才可以开始领取年金。
递延年金的终值和现值是计算递延年金投资效益的两个重要指标。
本文将介绍递延年金的终值和现值的概念、计算方法以及其在金融规划中的重要性。
一、递延年金的终值和现值的概念递延年金的终值是指递延期结束后,根据投资或保险产品的利率或收益率计算得出的最终支付金额。
终值的计算是基于投资本金、投资期限和利率来确定的。
递延年金的现值则是指将未来某一时期的一系列年金回流现值计算出来的金额。
现值是通过将未来支付的年金按照特定的折现率计算得出的。
二、递延年金的终值和现值的计算方法递延年金的终值可以使用以下公式进行计算:FV = PV x (1 + r)^n其中,FV表示终值,PV表示初始投资本金,r表示利率,n表示投资或保险期限。
递延年金的现值计算可以使用以下公式进行计算:PV = C x [(1 - (1 + r)^(-n)) / r]其中,PV表示现值,C表示每期年金支付金额,r表示利率,n表示投资或保险期限。
三、递延年金的终值和现值在金融规划中的重要性递延年金的终值和现值在金融规划中扮演着非常重要的角色。
首先,计算递延年金的终值和现值可以帮助投资者或保险人了解他们在特定期限内的投资收益或保险回报。
通过计算终值和现值,投资者或保险人可以更好地评估递延年金的风险和回报。
其次,递延年金的终值和现值可以帮助投资者或保险人进行财务规划。
通过计算终值和现值,投资者或保险人可以根据自己的资金需求和目标制定合理的投资或保险计划。
他们可以根据终值和现值的计算结果,决定是否需要增加投资额度或调整投资期限,以达到更好的财务目标。
此外,递延年金的终值和现值对于投资者或保险人的退休计划也非常重要。
递延年金可以作为一种退休储蓄工具,通过定期缴纳保费或投资款项,为将来的退休生活提供稳定的收入来源。
某投资项目预测的净现金流量见下表(万元),设资金基本贴现率为10%,则该项目的净现金值为()万元解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21 式中的分式ii n -+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式是先计算出n 期的普通年金现值,然后减去前s 期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。
解:本例因为涉及到年金当中的递延年金, 所以将年金系列一起先介 绍,然后解题年金 ,是指一定时期内每次等额收付款的系列款项, 通常记作 A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及 零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同, 可 分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介 绍普通年金与递延年金,其他的在后面介绍。
一、普通年金 ,是指从第一期起,在一定时期内 每期期末 等额发生的 系列收付款项,又称后付年金。
1. 普通年金现值公式为 :式中的分式 1 (1 i ) 称作“年金现值系数”,记为(P/A ,i ,n ), i可通过直接查阅 “1 元年金现值表” 求得有关的数值, 上式也可写作:P=A (P/A , i ,n ). 2. 例子: 租入某设备,每年年末需要支付租金 120 元,年复利 利率为 10%,则 5 年内应支付的租金总额的现值为:、递延年金 ,是指第一次收付款发生时间 与第一期无关 ,而隔若干P A (1 i)A (1 i) 2 A (1 i) ( n 1) A (1 i) n 1 (1 i) A 1 (1 i) n 120 1 (1 10%)10% 120 3.7908 455(元)期(假设为 s 期, s ≥1),后才开始发生的系列等额收付款项。
它是 普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1. 递延年金现值公式为 :期的普通年金现值 ,即得递延年金的现值,公式( 2)是先将些递延年金视为 (n-s ) 期普通年金,求出在第 s期的现值,然后再折算为第零期的现值。
=1000×(元)PAns1 (1 i ) n 1 (1 i) s A (P/ A,i,n) (P/ A,i,s) 1) 或P A 1 (1 i)(ns)i (1 i) A (P/ A,i,n s) (P/F,i,s)2) 上述 1)公式是先 计算出 n 期的普通年金现值,然后减去前 s2. 例子:某人在年初存入一笔资金,存满 5 年后每年年末取出1000 元,至第 10 年末取完,银行存款利率为 10%。
第四节递延年金终值与现值的计算第四节递延年金终值与现值的计算钭志斌丽水职业技术学院一、递延年金递延年金(Deferred Annuity)是指第一次年金收付形式发生在第二期或第二期以后的年金。
递延年金的支付形式如图2-8所示。
12 …mm+1m+2 …m+n递延期递延年金发生的期数二、递延年金终值计算由于递延期m与终值无关只需考虑递延年金发生的期数n。
计算公式如下:12 …mm+1m+2 …m+n递延期递延年金发生的期数【例2-11】农庄的累计净收益为多少?假设江南公司拟一次性投资开发某农庄,预计该农庄能存续15年,但是前5年不会产生净收益,从第6年开始,每年的年末产生净收益5万元。
在考虑资金时间价值的因素下,若农庄的投资报酬率为10%,该农庄给企业带来累计收益为多少?12 …55+15+2 …5+10递延期5递延年金发生的期数10求该农庄给企业带来的累计收益,实际上就是求递延年金终值。
根据=50000×(F/A,10%,10)=50000×153>.937=796850(元)12 …55+15+2 …5+10递延期5递延年金发生的期数10三、递延年金现值的计算递延年金的现值与递延期数相关,递延的期数越长,其现值越低。
递延年金的现值计算有三种方法:方法1:把递延期以后的年金套用普通年金公式求现值,然后再向前折现。
即:12 …mm+1m+2 …m+n递延期递延年金发生的期数方法2:把递延期每期期末都当作有等额的年金收付A,把递延期和以后各期看成是一个普通年金,计算出这个普通年金的现值再把递延期虚增的年金现值减掉即可。
即:12 …mm+1m+2 …m+n假设递延期内每期都有A收付方法3:先求递延年金终值,再折现为现值即12 …mm+1m+2 …m+n【例2-12】农庄的累计投资限额为多少?接例2-11,假设江南公司决定投资开发该农庄,根据其收益情况,该农庄的累计投资限额为多少?实质上,求现值12 …55+15+2 …5+10递延期5递延年金发生的期数10按第一种方法计算:P=50000×(P/A,10%,10)×(P/F,10%,5)=50000×6.1446×0.6209=190759.11(元)按第二种方法计算:P=50000×(P/A,10%,15)-50000×(P/A,10%,5)=50000×7.6061-50000×3.7908=190765.00(元)按第三种方法计算:P=50000×(F/A,10%,10)×(P/F,10%,15)=50000×15.9370×0.2394=190765.89(元)计算结果表明,该农庄的累计投资限额为190759.11元。
(5)递延年金终值和现值的计算递延年金由普通年金递延形成,递延的期数称为递延期,用m表示(m为大于0的整数)。
递延年金的第一次收付发生在第(m+1)期期末。
递延年金的形式如下图:递延年金终值递延年金的终值=A×(F/A,i,n),只与年金期有关,与递延期无关。
递延年金的现值递延年金的现值,与递延期有关。
递延年金的现值计算方法【应用举例】【例题】某递延年金为从第4期开始,每期期末支付10万元,共计支付6次,假设利率为4%,相当于现在一次性支付的金额是多少?(P/A,4%,6)=5.2421,(P/F,4%,3)=0.8890,(P/A,4%,9)=7.4353,(P/A,4%,3)=2.7751。
【分析】从图上可看出,递延期m=3,年金A=10万元,n=6。
第一种方法分段折现:将6个10万元按普通年金求现值的方法折算到第3期期末,再将6年期的普通年金现值由按复利现值的方法折算到第0年。
递延年金现值P=10×(P/A,4%,6)×(P/F,4%,3)=10×5.2421×0.8890=46.60(万元)第二种方法用减法:假设递延期每期期末也都有年金10万元,这样在0时点看就构成了普通年金的形式,一共有9个10万元,可将这9个10万元求普通年金的现值,然后再减去递延期3个10万元的普通年金现值,就可求出本题递延年金的现值。
即:递延年金现值P=10×(P/A,4%,9)-10×(P/A,4%,3)=10×7.4353-10×2.7751=46.602(万元)【例题】某递延年金为从第4期开始,每期期初支付10万元,共计支付6次,假设利率为4%,相当于现在一次性支付的金额是多少?(P/F,4%,2)=0.9246,(P/A,4%,6)=5.2421。
【分析】从图上可看出,递延期m=3,年金A=10万元,n=6。
递延年金现值P=10×(P/A,4%,6)×(P/F,4%,2)=10×5.2421×0.9246=48.47(万元)递延年金现值P=10×(P/A,4%,8)-10×(P/A,4%,2)=48.47(万元)递延年金的现值计算方法【应用举例】【例题】DL公司2019年12月10日欲购置一批电脑,销售方提出三种付款方案,具体如下:方案1:2019年12月10日付款10万元,从2021年开始,每年12月10日付款28万元,连续支付5次。
某投资项目预测的净现金流量见下表(万元),设资金基本贴现率为10%,则该项目的净现金值为()万元解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21 式中的分式ii n -+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式是先计算出n 期的普通年金现值,然后减去前s 期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。
财务管理》第二章重难点讲解及例题:递延年金终值和现值
递延年金终值和现值
(1)递延年金终值(已知从第二期或第二期以后等额收付的普通年金A,求FA)
递延年金是指第-次等额收付发生在第二期或第二期以后的普通年金。
图示如下:
求递延年金的终值与求普通年金的终值没有差别(要注意期数),递延年金终值与递延期无关。
如上图中,递延年金的终值为:FA=AX(F/A,i,n),其中,“n,,表示的是A的个数,与递延期无关。
(2)递延年金现值(已知从第二期或第二期以后等额收付的普通年金A,求PA)
方法-:把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第-次等额收付前-期的数值,再往前推递延期期数就得出递延年金的现值。
图示如下:
PA=AX(P/A,i,n)×(P/F,i,m)
方法二:把递延期每期期末都当作有等额的收付,把递延期和以后各期看成是-个普通年金,计算这个普通年金的现值,再把递延期多算的年金现值减去即可。
图示如下:
PA=AX(P/A,i,m+n)-A×(P/A,i,m)
【提示】方法-、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题,再求递延年金现值。
方法三:先求递延年金的终值,再将终值换算成现值,图示如下:
PA=A×(F/A,i,n)×(P/F,i,m+n)
【提示】递延年金现值计算公式中的“n”指的是等额收付的次数,即A的个数;递延期“m”的含义是,把普通年金(第-次等额收付发生在第1期期末)递延m期之后,就变成了递延年金(第-次等额收付发生在第W期期末,W>1)。
因此,可以按照下面的简便方法确定递延期m的数值:
(1)确定该递延年金的第-次收付发生在第几期末(假设为第W期末)(此时应该注意“下-期的期初相当于上-期的期末”);
(2)根据(W-1)的数值确定递延期m的数值。
【例题7.单选题】下列关于递延年金的说法中,错误的是()。
A.递延年金是指隔若干期以后才开始发生的系列等额收付款项
B.递延年金没有终值
C.递延年金现值的大小与递延期有关,递延期越长,现值越小
D.递延年金终值与递延期无关
【答案】B
【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项;递延年金存在终值,其终值的计算与普通年金是相同的;终值的大小与递延期无关;但是递延年金的现值与递延期是有关的,递延期越长,递延年金的现值越小,所以选项B的说法是错误的。
【例题8.计算题】张先生准备购买-套新房,开发商提供了三种付款方案让张先生选择:
(1)A方案,从第4年年末开始支付,每年年末支付20万元,-共支付8年;
(2)B方案,按揭买房,每年年初支付15万元,-共支付10年;
(3)C方案,从第4年年初开始支付,每年年末支付19万元,-共支付8年。
假设银行利率为5%,请问张先生应该选择哪种方案。
【答案】
A方案是递延年金的形式,由于第-次支付发生在第4年年末,所以,W=4,递延期m =4—1=3.
A方案付款的现值=20×(P/A,5%,8)×(P/F,5%,3)=20×6.4632×0.8638=111.66(万元)
B方案是预付年金的方式,由于-共支付10次,所以,n=10.
B方案付款的现值=15×[(P/A,5%,10—1)+1]=15×(7.1078+1)=121.62(万元)
C方案是递延年金形式,由于第-次支付发生在第4年年初(相当于第3年年末),所以,W=3,递延期m=3-1=2.
C方案付款的现值=19×(P/A,5%,8)×(P/F,5%,2)=19×6.4632×0.9070=111.38(万元)
由于C方案付款的现值最小,所以张先生应该选择C方案。
4.永续年金终值和现值
(1)永续年金终值
永续年金没有到期日,因此没有终值。
(2)永续年金现值(已知无限期等额收付的普通年金A,求PA)
永续年金的现值是普通年金现值的极限形式(n→∞):PA=A/i
【例题9.判断题】王先生打算在某高校建立-项永久性奖学金,款项-次性存入银行,-年后开始提款,每年提款-次,每次提款2万元用于奖励学生,假设银行存款年利率为4%,那么王先生应该存入银行50万元。
()
【答案】√
【解析】由于是永久性奖学金,并且每次发放的数额相同,所以,这是永续年金现值计算问题。
王先生应该-次性存入银行的款项=2/4%=50(万元)。
递延年金现值计算公式P=A×(P/A,i,n)×(P/F,i,m):
在递延期为m期的递延年金中,从第m+1期开始,属于典型的普通年金,n表示的是该普通年金中A的个数,所以,A×(P/A,i,n)表示的是折现到第(m+1)期期初(即第m期期末)的数值,而我们想求的递延年金现值是指第1期期初的数值,并且第(m+1)期期初距离第1期期初的间隔为m期,所以,应该对A×(P/A,i,n)进行复利折现m期,即P=A×(P/A,i,n)×(P/F,i,m)。
递延年金现值的计算公式P=A×(F/A,i,n)×(P/F,i,n+m):
使用这个公式计算递延年金现值实际上就是先求终值然后折现。
A×(F/A,i,n)计算的是等额收付n次的年金在第(m+n)期期末的终值,由于我们需要计算的是第1期期初的现值,所以需要在此基础上乘以(m+n)期的复利现值系数,即P=A×(F/A,i,n)×(P/F,i,n+m)。
递延年金现值的计算公式P=A×(P/A,i,n)×(P/F,i,m):
把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第一个等额收付前一期的数值,再往前推递延期期数就得出递延年金的现值。