如何确定递延年金现值计算公式复习过程

所示。 递延年金的支付形式如图2-8所示。
0 1 2… m m+1 m+2 … m+n
递延期
递延年金发生的期数
课程网站：http:\\
二、递延年金终值计算
由于递延期m与终值无关 只需考虑递延年金发生的期数n。
0 1 2… m m+1 m+2 … m+n
递延期
递延年金发生的期数
递延年金发生的期数10 递延年金发生的期数
课程网站：http:\\
三、递延年金现值的计算
递延年金的现值与递延期数相关，递延的期数越长， 递延年金的现值与递延期数相关，递延的期数越长， 其现值越低。 其现值越低。 递延年金的现值计算有三种方法： 递延年金的现值计算有三种方法：
求该农庄给企业带来的累计收益， 求该农庄给企业带来的累计收益，实际上就是求递 延年金终值。 延年金终值。
根据 F = A(F / A, i, n ) ＝50000×（F/A，10%，10） ＝50000×15.937 ＝796850（元）
0 1 2… 5 5+1 5+2 … 5+10
递延期5 递延期
主教材： 高等教育出版社 钭志斌《公司理财》
第四节 递延年金终值与现值的计算
钭志斌 丽水职业技术学院
课程网站：http:\\
一、递延年金
递延年金（ 递延年金（Deferred Annuity）是指第一次年 金收付形式发生在第二期或第二期以后的年金。 金收付形式发生在第二期或第二期以后的年金。
按第三种方法计算： 按第三种方法计算：
P＝50000×（F/A，10%，10）×（P/F， 10%，15） ＝50000×15.9370×0.2394 ＝190765.89（元）

例：ABC公司面临两个投资机会可供选择，A 项目是一个高科技项目，该领域市场竞争激烈， 如果经济发展迅速并且项目研制开发搞得好， 则能够取得较大的市场份额，获得较高的利润； 反之，将会获得较少的利润甚至亏损。B项目 是一个成熟的产品，市场发展稳定，销售前景 可以根据市场调研资料进行可靠的预测。经预 测发现未来的市场行情可能有三种情况：繁荣、 一般、衰退，每种情况发生的可能概率以及各 种情况下的预期报酬率资料见表：
i
例




例：某企业要建立一项永久性的奖励基金，计 划每年发放500000元，在年利率为8％的情况 下，该企业现在应该存入银行多少元? P=A÷i＝500000÷8％＝6 250 000(元) 例：某企业在第一年年初向银行借入100万元， 银行规定从第一年到第五年每年年末应等额偿 还25.6万元，试计算利率？ i=A/P=25.6÷100=25.6%





（二）递延期m的确定： （1）首先搞清楚该递延年金的第一次收付发生在第几期末（假设为第W 期末）； （2）然后根据（W-1）的数值即可确定递延期m的数值； 注意：在确定“该递延年金的第一次收付发生在第几期末”时，应该记住 “本期的期初和上期的期末”是同一个时间点。 〔例1〕 某递延年金从第4年开始，每年年末支付A元。 〔解答〕由于第一次发生在第4期末，所以，递延期m＝4-1＝3 〔例2〕 某递延年金从第4年开始，每年年初支付A元。 〔解答〕由于第一次发生在第4期初（即第3期末），所以，递延期m＝31＝2 （三）下面把上述的内容综合在一起，计算一下各自的现值： 〔例1〕 某递延年金从第4年起，每年年末支付A元，直至第8年年末为止。 〔解答〕由于n=5，m=3，所以，该递延年金的现值为： A[（PVAi,8）-（PVAi,3）]或A（PVAi,5）×（PVi,3） 〔例2〕 某递延年金从第4年起，每年年初支付A元，直至第8年年初为止。 〔解答〕由于n=5，m=2，所以，该递延年金的现值为： A[（PVAi,7）-（PVAi,2）]或 A（PVAi,5）×（PVi,2）

递延年金的计算技巧年金是《财务管理》课程中的基础知识，其计算是学生在学习过程中的一个重点和难点。

年金包括普通年金、预付年金、递延年金和永续年金，后面三种年金的计算都是建立在普通年金终值和现值计算的基础之上，本文以多种方法来详细阐述递延年金的计算技巧，以此起到举一反三的目的。

标签：递延年金；计算；技巧年金是《财务管理》中的一个非常重要的概念，也是学习该门课程的基础，包括普通年金、预付年金、递延年金和永续年金，后面三种年金的计算都是建立在普通年金终值和现值计算的基础之上，但是也可以举一反三，灵活运用多种方法进行计算，本文就以递延年金的计算技巧为例来进行说明。

一、年金的概念年金是指一定时期内等额、定期的系列收付款项。

比如购买住房的分期还贷、企业或个人租房定期等额支付的租金等都属于年金的形式。

在年金的计算过程中，需要注意以下两个方面的问题：1.现值和终值的含义现值是未来货币的现在值，是每期等额系列收付款项的复利现值之和。

终值是现在货币的未来值，是每期等额系列收付款项的复利终值之和。

在教学中通常以时间轴的形式来形象的解释这两个概念。

时间轴上的“1、2、3……n”代表该期期末，即“1”代表第一期期末，“2”代表第2期期末。

“0”代表第一期期初，也就是发生第一笔等额收付款项的期初，一般理解为现在的时点，计算的现值就是在这个时点上的价值。

“n”代表第n期期末，也就是发生第n笔等额收付款项的期末，计算的终值就是在这个时点上的价值。

2.期数的界定在学习年金时，教材后面均附有年金终值系数表和年金现值系数表，表里面列示的是根据期数和利率所计算的对应的终值系数和现值系数，方便学生快速的计算年金的相关题目。

但是，在教学过程中发现，学生经常犯的错误就是把期数等同于年。

其实，系数表里面的“期数”，既可以是年的概念，也可以是半年、季度或月的概念。

重要的是一定要把期数和利率对应起来，即期数是年，就对应年利率；期数是半年，就对应半年利率；期数是季度，就对应季度利率；期数是月，就对应月利率。

编辑ppt
3
例：某企业采用补偿贸易方式引进国外一条先 进的生产线，协议中约定生产线投产后从第4 年年末开始，连续5年用该生产线生产出的价 值500 000元的产品偿还设备的价款。若银行 存款年利率为6％，则到最后一期设备款支付 完毕为止该公司共支付货款多少元?
F＝A× (F／A，i，n) ＝A×(F／A，6％，5)
因此，可以说你的股票投资是一项有风险的投 资
编辑ppt
13
（二）风险的分类
1、按风险能否分散分----不可分散风险（市场风险） 和可分散风险(公司特有风险)
不可分散风险是指影响所有公司的因素带来的风险 ， 通货膨胀、经济衰退、战争
可分散风险是指发生于个别公司的特有事件给企业 带来的风险 ，如开发新产品失败、诉讼失败
式推导得出。公式 ：永续年金现值 P A
编辑ppt
i8
例
例：某企业要建立一项永久性的奖励基金，计 划每年发放500000元，在年利率为8％的情况 下，该企业现在应该存入银行多少元?
P=A÷i＝500000÷8％＝6 250 000(元) 例：某企业在第一年年初向银行借入100万元，
银行规定从第一年到第五年每年年末应等额偿 还25.6万元，试计算利率？ i=A/P=25.6÷100=25.6%
编辑ppt
12
投资风险的概念 (续)
例2：设你现在投资10000元购买深发展股票 1000股（每股10元）。那么，一年后你的股票 价值是多少？
（1） 一年后，股票价值11000元。则你的投 资收益率K=（11000-10000）/10000= 10%
（2） 一年后，股票价值为9500元，则你的投 资收益K=（9500-10000）/10000= －5%

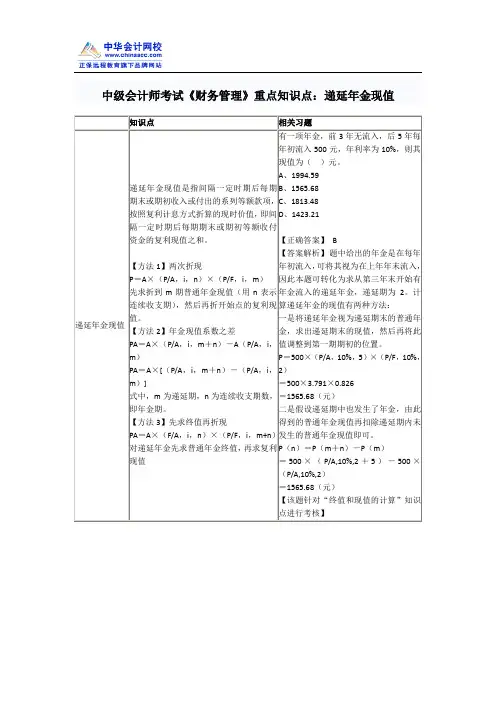
如何确定递延年金现值计算公式如何确定递延年金现值计算公式P=A[(P/A,i,n)－(P/A,i,s)]= A(P/A,i,n-s)×(P/F,i,s)中的期数n和s的数值? ㈠确定n的数值：“n”的数值就是递延年金中最后一次收付距离第一年年初的间隔期数。

举例如下：⑴如果某一递延年金是从第4年起，每年年初发生，直至第8年年初为止，由于从第一年初到第八年初共计间隔7年，所以，n=7⑵如果某一递延年金是从第4年起，每年年末发生，直至第8年年末为止，由于从第一年初到第八年年末共计间隔8年，所以，n=8⑶如果某一递延年金是从第4年起，每半年年初发生，直至第8年年初为止，由于从第一年初到第八年初共计间隔7年，所以，n=7×2＝14⑷如果某一递延年金是从第4年起，每半年年末发生，直至第8年年末为止，由于从第一年初到第八年年末共计间隔8年，所以，n=8×2＝16㈡递延期间s的确定方法：⑴首先搞清楚该递延年金的第一次收付发生在第几期末（假设为第W期末）；⑵然后根据（W-1）的数值即可确定递延期间s的数值；在确定“该递延年金的第一次收付发生在第几期末”时，应该记住“上一期的期末就是下一期的期初”。

㈢举例说明：⑴假如某递延年金为从第4年开始，每年年末支付A元，则由于第一次收付发生在第四年末，即第四期末，所以，递延期间为：4－1＝3；⑵假如某递延年金为从第4年开始，每年年初支付A元，则由于第一次收付发生在第四年初，即第三期末，所以，递延期间为：3－1＝2；⑶假如某递延年金为从第4年开始，每半年年初支付A元，则由于第一次收付发生在第四年初，即第六个半年末，属于第六期末，所以，递延期间为：6－1＝5；⑷假如某递延年金为从第4年开始，每半年年末支付A元，则由于第一次收付发生在第四年半，即第七个半年末，属于第七期末，所以，递延期间为：7－1＝6；。

中级会计师考试《财务管理》重点知识点：递延年金现值
知识点
相关习题
递延年金现值
递延年金现值是指间隔一定时期后每期期末或期初收入或付出的系列等额款项，按照复利计息方式折算的现时价值，即间隔一定时期后每期期末或期初等额收付资金的复利现值之和。
【方法1】两次折现
P＝A×（P/A，i，n）×（P/F，i，m）
对递延年金先求普通年金终值，再求复利现值
有一项年金，前3年无流入，后5年每年初流入500元，年利率为10%，则其现值为（ ）元。
A、1994.59
B、1565.68
C、1813.48
D、1423.21
【正确答案】B
【答案解析】题中给出的年金是在每年年初流入，可将其视为在上年年末流入，因此本题可转化为求从第三年末开始有年金流入的递延年金，递延期为2。计算递延年金的现值有两种方法：
一是将递延年金视为递延期末的普通年金，求出递延期末的现值，然后再将此值调整到第一期期初的位置。
Hale Waihona Puke P＝500×（P/A，10%，5）×（P/F，10%，2）
＝500×3.791×0.826
＝1565.68（元）
二是假设递延期中也发生了年金，由此得到的普通年金现值再扣除递延期内未发生的普通年金现值即可。
P（n）＝P（m＋n）－P（m）
先求折到m期普通年金现值（用n表示连续收支期），然后再折开始点的复利现值。
【方法2】年金现值系数之差
PA＝A×（P/A，i，m＋n）－A（P/A，i，m）
PA＝A×[（P/A，i，m＋n）－（P/A，i，m）]
式中，m为递延期，n为连续收支期数，即年金期。
【方法3】先求终值再折现
PA＝A×（F/A，i，n）×（P/F，i，m+n）

财务管理》第二章重难点讲解及例题：递延年金终值和现值递延年金终值和现值（1）递延年金终值（已知从第二期或第二期以后等额收付的普通年金A，求FA）递延年金是指第－次等额收付发生在第二期或第二期以后的普通年金。

图示如下：求递延年金的终值与求普通年金的终值没有差别（要注意期数），递延年金终值与递延期无关。

如上图中，递延年金的终值为：FA＝AX（F／A，i，n），其中，“n，，表示的是A的个数，与递延期无关。

（2）递延年金现值（已知从第二期或第二期以后等额收付的普通年金A，求PA）方法－：把递延期以后的年金套用普通年金公式求现值，这时求出的现值是第－次等额收付前－期的数值，再往前推递延期期数就得出递延年金的现值。

图示如下：PA＝AX（P／A，i，n）×（P／F，i，m）方法二：把递延期每期期末都当作有等额的收付，把递延期和以后各期看成是－个普通年金，计算这个普通年金的现值，再把递延期多算的年金现值减去即可。

图示如下：PA＝AX（P／A，i，m＋n）－A×（P／A，i，m）【提示】方法－、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题，再求递延年金现值。

方法三：先求递延年金的终值，再将终值换算成现值，图示如下：PA＝A×（F／A，i，n）×（P／F，i，m＋n）【提示】递延年金现值计算公式中的“n”指的是等额收付的次数，即A的个数；递延期“m”的含义是，把普通年金（第－次等额收付发生在第1期期末）递延m期之后，就变成了递延年金（第－次等额收付发生在第W期期末，W>1）。

因此，可以按照下面的简便方法确定递延期m的数值：（1）确定该递延年金的第－次收付发生在第几期末（假设为第W期末）（此时应该注意“下－期的期初相当于上－期的期末”）；（2）根据（W－1）的数值确定递延期m的数值。

【例题7.单选题】下列关于递延年金的说法中，错误的是（）。

A.递延年金是指隔若干期以后才开始发生的系列等额收付款项B.递延年金没有终值C.递延年金现值的大小与递延期有关，递延期越长，现值越小D.递延年金终值与递延期无关【答案】B【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项；递延年金存在终值，其终值的计算与普通年金是相同的；终值的大小与递延期无关；但是递延年金的现值与递延期是有关的，递延期越长，递延年金的现值越小，所以选项B的说法是错误的。

2、计算期望报酬或率（期望值），也称均值
期望报酬率是一个概率分布中的所有可能结果，以
各自相应的概率为权数计算的加权平均数，是加权
平均的中心值。反映随机变量取值的平均化，是随
机变量的集中趋势，其计算公式如下：
n
期望报酬
EXi
p某种期望 该 报种 酬报酬发生 i
i1
例
例：甲方案收益额有三种可能结果，每种结果出现 的机会比例（概率）如下：
（1）递延年金的终值 递延年金的终值计算与递延期无关，其计算方法
与普通年金终值相同。
例题
例： 假设图中所示，第一次支付在第三 年末，并连续支付3年，年利率为10％， 每年等额支付1000元，递延年金的终值 是多少元?
递延年金终值F＝A×(F／A，i，n-s) ＝1000×(F／A，10％，3) =1000×3.31
i
例
例：某企业要建立一项永久性的奖励基金，计 划每年发放500000元，在年利率为8％的情况 下，该企业现在应该存入银行多少元?
P=A÷i＝500000÷8％＝6 250 000(元) 例：某企业在第一年年初向银行借入100万元，
银行规定从第一年到第五年每年年末应等额偿 还25.6万元，试计算利率？ i=A/P=25.6÷100=25.6%
因为C、D两项目期望值不同，所以不能直接根据 标准差比较风险大小，D项目虽然标准差大，但风险 不一定比C项目大。需要计算两项目标准离差率进行 比较。
C项目标准离差率=180÷200=0.9
D项目标准离差率=200÷250=0.8
比较两项目标准离差率，C项目离散程度大，所以 C项目比D项目风险大。
二、风险与报酬的关系
风险报酬也叫风险收益或风险价值，是指投 资者由于冒风险进行投资而获得的超过货币时 间价值的额外收益。

定期评估和调整
长期投资视野
定期评估投资组合的表现和市场环境，并 根据需要进行调整，以保持风险和回报的 平衡。
递延年金通常需要长期投资视野，通过坚 持长期投资策略，投资者可以更好地平衡 风险和回报，实现长期的资本增值目标。
感谢您的观看
THANKS
并在债券到期时获得本金回报，而递延 期限，而递延年金的计算则需要考虑递
年金的投资者需要在未来某一特定时期
延期间和支付时间。
开始获得回报。
05
递延年金的风险与回报分 析
风险分析
市场风险
递延年金投资涉及市场风险， 市场波动可能导致投资价值的
不稳定。
信用风险
投资于债券或其他债务工具的 递延年金可能面临发行方违约 的信用风险。
递延年金现值的影响因素
01
02
03
04
年利率
年利率越高，递延年金现值越 小。
每年支付的金额
每年支付的金额越大，递延年 金现值越大。
递延期数
递延期数越长，递延年金现值 越小。
递延年金的期数
递延年金的期数越长，递延年 金现值越大。
04
递延年金与其他金融工具 的比较
与普通年金的比较
普通年金是每年或每月固定时间支付的款项，而递延年金是在未来某一特定时期开 始支付的款项。
利率风险
固定收益的递延年金在利率变 动时可能面临投资回报的不确 定性。
流动性风险
某些递延年金可能面临流动性 风险，即难以在需要时以期望
价格出售。
回报分析
预期回报
根据投资策略和风险承受能力，投资 者预期从递延年金中获得一定的回报。
投资组合多样化
通过将资金分配到不同资产类别和行 业，递延年金旨在实现回报和风险的 平衡。

递延年金的名词解释|计算方法是什么递延年金的名词解释：递延年金又称“延期年金”，是指在最初若干期没有收付款项的情况下，后面若干期等额的系列收付款项。

它是普通年金的特殊形式。

普通年金又称“后付年金”，是指每期期末有等额的收付款项的年金。

这种年金形式是在现实经济生活中最为常见。

普通年金终值犹如零存整取的本利和，它是一定时期内每期期末等额收付款项的复利终值之和。

递延年金的计算方法：假设最初有m期没有收付款项，后面n期有等额的收付款项，则延期年金的现值即为后n期年金贴现至m期第一期期初的现值。

其计算公式为：V0=A*PVIFAi,n*PVIFi,m 延期年金现值还可以用另外一种方法计算，先求出m+n期后付年金现值，减去没有付款的前m 期后付年金现值，二者之差便是延期m期的n期后付年金现值。

其计算公式为：V0=A*PVIFAi,m+n−A*PVIFAi,m=A*(PVIFAi,m+n−PVIFAi,m)例：某企业向银行借入一笔款项，银行贷款的年利息率为8%，银行规定前10年不用还本付息，但从第11年至第20年每年年末偿还本息1000元，问这笔款项的现值应为多少?第一种计算方法就是先按照普通年金计算出年金在m期期末的现值，然后再复利折现m期就是递延年金的现值。

第二种计算方法就是假设前m期也有年金发生，那么就构成了一个普通年金，按照m+n期计算出年金现值后再减去假设存在的m期的年金现值就是递延年金的现值。

第三种计算方法的含义就是先按照普通年金终值的计算方法计算出递延年金的终值，然后再复利折现到0时点计算出递延年金的现值。

具体结合图示讲解如下：方法一：把递延期以后的年金套用普通年金公式求现值，这时求出来的现值是第一个等额收付前一期的数值，再往前推递延期期数就得出了递延年金的现值。

图示如下：递延年金的终值计算与普通年金的终值计算一样，计算公式如下:FA =A (F/A , i , n)注意式中" n" 表示的是A 的个数，与递延期无关。

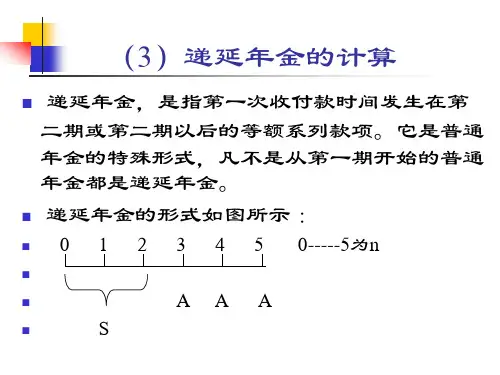
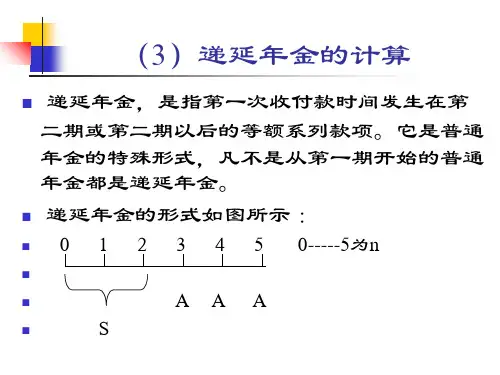
第四节递延年金终值与现值的计算第四节递延年金终值与现值的计算钭志斌丽水职业技术学院一、递延年金递延年金（Deferred Annuity）是指第一次年金收付形式发生在第二期或第二期以后的年金。

递延年金的支付形式如图2-8所示。

12 …mm+1m+2 …m+n递延期递延年金发生的期数二、递延年金终值计算由于递延期m与终值无关只需考虑递延年金发生的期数n。

计算公式如下：12 …mm+1m+2 …m+n递延期递延年金发生的期数【例2-11】农庄的累计净收益为多少？假设江南公司拟一次性投资开发某农庄，预计该农庄能存续15年，但是前5年不会产生净收益，从第6年开始，每年的年末产生净收益5万元。

在考虑资金时间价值的因素下，若农庄的投资报酬率为10%，该农庄给企业带来累计收益为多少？12 …55+15+2 …5+10递延期5递延年金发生的期数10求该农庄给企业带来的累计收益，实际上就是求递延年金终值。

根据＝50000×（F/A，10%，10）＝50000×153>.937＝796850（元）12 …55+15+2 …5+10递延期5递延年金发生的期数10三、递延年金现值的计算递延年金的现值与递延期数相关，递延的期数越长，其现值越低。

递延年金的现值计算有三种方法：方法1：把递延期以后的年金套用普通年金公式求现值，然后再向前折现。

即：12 …mm+1m+2 …m+n递延期递延年金发生的期数方法2：把递延期每期期末都当作有等额的年金收付A，把递延期和以后各期看成是一个普通年金，计算出这个普通年金的现值再把递延期虚增的年金现值减掉即可。

即：12 …mm+1m+2 …m+n假设递延期内每期都有A收付方法3：先求递延年金终值，再折现为现值即12 …mm+1m+2 …m+n【例2-12】农庄的累计投资限额为多少？接例2-11，假设江南公司决定投资开发该农庄，根据其收益情况，该农庄的累计投资限额为多少？实质上，求现值12 …55+15+2 …5+10递延期5递延年金发生的期数10按第一种方法计算：P＝50000×（P/A，10%，10）×（P/F，10%，5）＝50000×6.1446×0.6209＝190759.11（元）按第二种方法计算：P＝50000×（P/A，10%，15）－50000×（P/A，10%，5）＝50000×7.6061－50000×3.7908＝190765.00（元）按第三种方法计算：P＝50000×（F/A，10%，10）×（P/F，10%，15）＝50000×15.9370×0.2394＝190765.89（元）计算结果表明，该农庄的累计投资限额为190759.11元。

第二章：
复利现值系数（P/F，i,n）＝（1＋i）－n
复利终值系数（F/P，i,n）＝（1＋i）n
普通年金现值系数（P/A，i,n）＝[1－（1＋i）－n]/ i
普通年金终值系数（F/A，i,n）＝[（1＋i）n－1]/ i
偿债基金系数（A/F，i,n）= i /[（1＋i）n－1]
资本回收系数（A/P，i,n）＝i /[1－（1＋i）－n]
即付年金现值系数＝[1－（1＋i）－n]/ i×（1＋i）
即付年金终值系数＝[（1＋i）n－1]/ i×（1＋i）
所以，很容易看出下列关系：
（1）复利现值系数（P/F，i,n）×复利终值系数（F/P，i,n）＝1
普通年金现值系数（P/A，i,n）×资本回收系数（A/P，i,n）＝1
普通年金终值系数（F/A，i,n）×偿债基金系数（A/F，i,n）＝1
（2）普通年金现值系数（P/A，i,n）＝[1－复利现值系数（P/F，i,n）]/ i
普通年金终值系数（F/A，i,n）＝[复利终值系数（F/P，i,n）－1]/ i
（3）即付年金现值系数＝普通年金现值系数（P/A，i,n）×（1＋i）
即付年金终值系数＝普通年金终值系数（F/A，i,n）×（1＋i）
（4）复利现值系数（P/F，i,n）×普通年金终值系数（F/A，i,n）＝普通年金现值系数（P/A，i,n）复利终值系数（F/P，i,n）×普通年金现值系数（P/A，i,n）＝普通年金终值系数（F/A，i,n）。

注册税务师考试辅导《财务与会计》第一章讲义4递延年金（6）递延年金递延年金不是从第一期就开始发生年金，而是在几期以后每期末发生相等数额的款项，递延年金终值的计算和普通年金终值的计算一样，递延年金现值的计算要受到递延期的影响。

递延年金现值计算的两种方法：方法1：P＝A×（PVAr,m＋n－PVAr,m）方法2：P＝A×PVAr,n×PVr,m经典例题－12【基础知识题】企业计划投资一个项目，需要投资500万元，项目建设期3年，可以使用l0年，每年产生收益90万元。

如果企业要求的报酬率为9%，问投资项目是否可行？[答疑编号6312010206]因为项目的建设期为3年，所以是递延年金问题，根据前面公式：P＝90×（7.4869—2.5313）＝446.004（万元）由于收回的资金小于投资数额，该项目不可行。

利用第二个公式计算得：P＝90×6.4177×0.7722＝446.02（万元）同样，该项目不可行。

经典例题－13【单选题】A企业购建一条新的生产线，该生产线预计可以使用5年，估计每年年末的现金净流量为25万元，假设年利率为12%，则该生产线未来现金净流量的现值为（）万元。

（PV12%,5＝0.5674，PVA12%,5＝3.6048）A.14.185B.90.12C.92D.100[答疑编号6312010207]『正确答案』B『答案解析』未来现金净流量现值＝25×PVA 12%,5＝25×3.6048＝90.12（万元）经典例题－14【单选题】某公司决定分别在2002年、2003年、2004年和2005年的1月1日各存入5 000元，按10%利率，每年复利一次，则2005年1月1日的本利和为（）。

（FVA10%,4＝4.6410）A.10 000B.15 000C.23 205D.25 205[答疑编号6312010208]『正确答案』C『答案解析』由于下一年初就是上一年末，所以，本题可以理解为从2001年开始，每年年末存入5000元，计算到2004年末的本利和，因此，这道题是期数为4期的普通年金终值的计算问题。

4.计算普通股的资本成本的时候分子为什么有时需要乘以 1＋g，有时不乘？
第3页
2020 年税务师考试辅导
财务与会计
【答复】 公式： 普通股的资本成本＝预计下一年的股利/[当前股价×（1－筹资费用率）]＋股利 增长率 说明： 如果已知上年股利为 D0，计算公式中的预计下一年的股利 D 等于 D0（1＋g）。 （1）“D0”指的是最近一期已经发放的股利； （2）“D”指的是还未发放或最近一期即将发放的股利。 （3）“D0”与“D”的本质区别是，与“D0”对应的股利“已经收到”，而与“D” 对应的股利“还未收到”。 例题：甲公司发行普通股筹资金额 1000 万元，当前股票市价是每股 20 元，今年 的股利为 2.2，股利增长率为 2%，筹资费用率为 0，所得税税率为 25%，则普通 股资本成本为（ ）。 A.10.00% B.10.27% C.11.00% D.13.22% 【答案】D 【解析】普通股的资本成本＝2.2×（1＋2%）/20＋2%＝13.22%
2020 年税务师考试辅导
财务与会计
1.如何确定递延年金现值计算公式中的递延期 m 的数值？ 【答复】 公式： 递延年金现值： P＝A×（P/A，i，n）×（P/F，i，m） ＝A×[（P/A，i，m＋n）－（P/A，i，m）] ＝A×（F/A，i，n）×（P/F，i，m＋n） 说明： （1）首先搞清楚该递延年金的第一次收付发生在第几期末（假设为第 W 期末）； （2）然后根据（W-1）的数值即可确定递延期 m 的数值； 注意：在确定“该递延年金的第一次收付发生在第几期末”时，应该记住“本期 的期初和上期的期末”是同一个时间点。 〔例〕某递延年金从第 4 年开始，每年年末支付 A 元。由于第一次发生在第 4 期末，所以，递延期 m＝4－1＝3 〔例 2〕某递延年金从第 4 年开始，每年年初支付 A 元。由于第一次发生在第 4 期初（即第 3 期末），所以，递延期 m＝3－1＝2 例题：甲公司拟投资一项目，该项目存续期为 10 年，前 3 年无现金流出，后 7 年每年年初现金流出 320 万元，假设年利率为 8%，则该项年金的现值是（ ） 万元。[已知（P/A，8%，7）＝5.2064，（P/F，8%，2）＝0.8573] A.1428.30 B.1322.50 C.1513.12 D.1666.04 【答案】A 【 解 析 】 该 项 年 金 的 现 值 ＝ 320× （ P/A ， 8% ， 7 ） × （ P/F ， 8% ， 2 ） ＝ 320×5.2064×0.8573＝1428.30（万元）

关于递延年⾦在年末付,最终折现的时点是不是第⼀年年末?如果是年初付的形式呢?有什么规律吗?
折现的时点，当然都是现在即时点为0了。

你可以采⽤画数轴的⽅法。

⽐如说，前三年没有现⾦流⼊，后四年：
　（1）每年末流⼊1000元，那么画在数轴上就是前三年是空的，后四年每年末流⼊1000元，第⼀步折现1000（P/A，i，4）时点为第四年初即第三年末，再折现到现在是三期折现即1000（P/A，i，4）（P/F，i.3）
　（2）每年初流⼊1000元，那么画在数轴上就是前⼆年是空的，从第三年末即第四年初每年末流⼊1000元，第⼀步折现1000（P/A，i，4）时点为第三年初即第⼆年末，再折现到现在是⼆期折现即1000（P/A，i，4）（P/F，i.2）。

你可以按我的讲解在纸上画⼀下。

画完以后你就会明⽩，这样的题画数轴可以“⼀⽬了然”，不易出错。

画数轴是解这类题的⽅法。

（3）如果某递延年金是从第4年起，每半年年初发生，直至第8年年初为止， 由于从第一年初到第八年初共计间隔7年，而此时是“半年为一期”，所以，
n=7×2＝14 （4）如果某递延年金是从第4年起，每半年年末发生，直至第8年年末为止， 由于从第一年初到第八年年末共计间隔8年，而此时是“半年为一期”，所以，
＝33l0(元)
例：某企业采用补偿贸易方式引进国外一条先 进的生产线，协议中约定生产线投产后从第4 年年末开始，连续5年用该生产线生产出的价 值500 000元的产品偿还设备的价款。若银行 存款年利率为6％，则到最后一期设备款支付 完毕为止该公司共支付货款多少元?
F＝A× (F／A，i，n) ＝A×(F／A，6％，5)
（3）递延年金的计算
递延年金，是指第一次收付款时间发生在第
二期或第二期以后的等额系列款项。它是普通 年金的特殊形式，凡不是从第一期开始的普通 年金都是递延年金。
递延年金的形式如图所示 ：
0 1 2 3 4 5 0-----5为n
AA A
S
递延年金的计算
从图可以看出，前2期没有支付，而从第三期期末开 始连续支付3期。由于其开始支付不在第一期，所以 我们称它为递延年金。前2期没有支付，我们称其为 递延期，用S表示，S＝2 。n＝5。
〔解答〕由于共计发生5次，所以，n=5
〔例2〕某递延年金从第4年起，每年年初支付A 元，直至第8年年初为止。
〔解答〕由于共计发生5次，所以，n=5
（二）递延期m的确定： （1）首先搞清楚该递延年金的第一次收付发生在第几期末（假设为第W
期末）；
（2）然后根据（W-1）的数值即可确定递延期m的数值；
A[（P/A,i,8）-(P/A,i,3)＝A（P/A,i,8-3）×(P/F,i,3) ＝A（P/A,i,5） ×(P/F,i,3)

递延年金推导公式递延年金推导公式1. 基本概念•递延年金：指在一定时间内，每期固定金额的年金推迟支付，从推迟时间后开始支付的金融产品。

•推导公式：用于计算递延年金的特定数学公式。

2. 列举递延年金推导公式•递延年金终值公式：–FV=P×(1+i)n•递延年金现值公式：–PV=P(1+i)n•递延年金常规支付公式：–PMT=P×i1−(1+i)−n•递延年金提前支付公式：–PMT=P×i1−(1+i)−(n+1)3. 解释和举例递延年金终值公式递延年金终值公式用于计算在一定时间内，每期固定金额的递延年金的未来价值。

其中，FV代表递延年金的终值，P代表每期支付金额，i代表每期利率，n代表支付期数。

举例：假设某人从30岁开始，每月向银行存入1000元，年利率为5%，并希望在退休时享受递延年金。

如果他计划到退休时的60岁，那么使用递延年金终值公式可计算出：$FV = 1000 (1 + )^{30} = 1000 = $元因此，到退休时，他的递延年金终值将达到元。

递延年金现值公式递延年金现值公式用于计算在一定时间内，每期固定金额的递延年金的现值。

其中，PV代表递延年金的现值，P代表每期支付金额，i 代表每期利率，n代表支付期数。

举例：假设某人计划从40岁开始，每月向保险公司交付500元，保险公司保证退休时从60岁起每月支付递延年金。

如果退休时的利率为4%，那么使用递延年金现值公式可计算出：$PV = = = $元因此，他每月交付给保险公司的现值为元。

递延年金常规支付公式递延年金常规支付公式用于计算在一定时间内，每期金额相同的递延年金的每期支付金额。

其中，PMT代表递延年金的每期支付金额，P代表每期支付金额，i代表每期利率，n代表支付期数。

举例：假设某人计划从50岁开始，每年向银行存入5000元，存款利率为6%，并希望从65岁开始每年提取递延年金。

使用递延年金常规支付公式可计算出：$PMT = 5000 = 5000 = $元因此，他每年从65岁开始可获得元的递延年金。