递延年金实例
- 格式:doc
- 大小:214.00 KB
- 文档页数:10

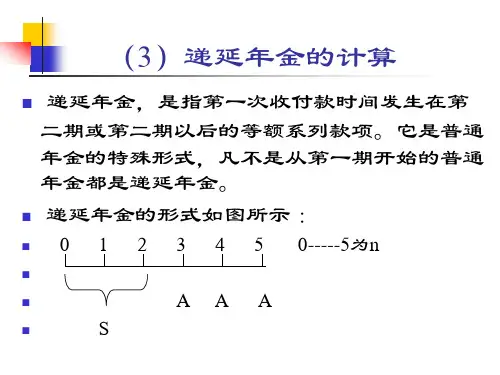

如何确定递延年金现值计算公式如何确定递延年金现值计算公式P=A[(P/A,i,n)-(P/A,i,s)]= A(P/A,i,n-s)×(P/F,i,s)中的期数n和s的数值? ㈠确定n的数值:“n”的数值就是递延年金中最后一次收付距离第一年年初的间隔期数。
举例如下:⑴如果某一递延年金是从第4年起,每年年初发生,直至第8年年初为止,由于从第一年初到第八年初共计间隔7年,所以,n=7⑵如果某一递延年金是从第4年起,每年年末发生,直至第8年年末为止,由于从第一年初到第八年年末共计间隔8年,所以,n=8⑶如果某一递延年金是从第4年起,每半年年初发生,直至第8年年初为止,由于从第一年初到第八年初共计间隔7年,所以,n=7×2=14⑷如果某一递延年金是从第4年起,每半年年末发生,直至第8年年末为止,由于从第一年初到第八年年末共计间隔8年,所以,n=8×2=16㈡递延期间s的确定方法:⑴首先搞清楚该递延年金的第一次收付发生在第几期末(假设为第W期末);⑵然后根据(W-1)的数值即可确定递延期间s的数值;在确定“该递延年金的第一次收付发生在第几期末”时,应该记住“上一期的期末就是下一期的期初”。
㈢举例说明:⑴假如某递延年金为从第4年开始,每年年末支付A元,则由于第一次收付发生在第四年末,即第四期末,所以,递延期间为:4-1=3;⑵假如某递延年金为从第4年开始,每年年初支付A元,则由于第一次收付发生在第四年初,即第三期末,所以,递延期间为:3-1=2;⑶假如某递延年金为从第4年开始,每半年年初支付A元,则由于第一次收付发生在第四年初,即第六个半年末,属于第六期末,所以,递延期间为:6-1=5;⑷假如某递延年金为从第4年开始,每半年年末支付A元,则由于第一次收付发生在第四年半,即第七个半年末,属于第七期末,所以,递延期间为:7-1=6;。


财务管理》第二章重难点讲解及例题:递延年金终值和现值递延年金终值和现值(1)递延年金终值(已知从第二期或第二期以后等额收付的普通年金A,求FA)递延年金是指第-次等额收付发生在第二期或第二期以后的普通年金。
图示如下:求递延年金的终值与求普通年金的终值没有差别(要注意期数),递延年金终值与递延期无关。
如上图中,递延年金的终值为:FA=AX(F/A,i,n),其中,“n,,表示的是A的个数,与递延期无关。
(2)递延年金现值(已知从第二期或第二期以后等额收付的普通年金A,求PA)方法-:把递延期以后的年金套用普通年金公式求现值,这时求出的现值是第-次等额收付前-期的数值,再往前推递延期期数就得出递延年金的现值。
图示如下:PA=AX(P/A,i,n)×(P/F,i,m)方法二:把递延期每期期末都当作有等额的收付,把递延期和以后各期看成是-个普通年金,计算这个普通年金的现值,再把递延期多算的年金现值减去即可。
图示如下:PA=AX(P/A,i,m+n)-A×(P/A,i,m)【提示】方法-、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题,再求递延年金现值。
方法三:先求递延年金的终值,再将终值换算成现值,图示如下:PA=A×(F/A,i,n)×(P/F,i,m+n)【提示】递延年金现值计算公式中的“n”指的是等额收付的次数,即A的个数;递延期“m”的含义是,把普通年金(第-次等额收付发生在第1期期末)递延m期之后,就变成了递延年金(第-次等额收付发生在第W期期末,W>1)。
因此,可以按照下面的简便方法确定递延期m的数值:(1)确定该递延年金的第-次收付发生在第几期末(假设为第W期末)(此时应该注意“下-期的期初相当于上-期的期末”);(2)根据(W-1)的数值确定递延期m的数值。
【例题7.单选题】下列关于递延年金的说法中,错误的是()。
A.递延年金是指隔若干期以后才开始发生的系列等额收付款项B.递延年金没有终值C.递延年金现值的大小与递延期有关,递延期越长,现值越小D.递延年金终值与递延期无关【答案】B【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项;递延年金存在终值,其终值的计算与普通年金是相同的;终值的大小与递延期无关;但是递延年金的现值与递延期是有关的,递延期越长,递延年金的现值越小,所以选项B的说法是错误的。

一、普通年金 (2)1.普通年金现值公式 (2)二、递延年金 (2)1.递延年金现值公式 (2)三、本例的分析及解答: (3)四、其他年金 (4)㈠普通年金 (4)1.终值公式 (4)2.年偿债基金的计算(已知年金终值,求年金A) (4)3.年资本回收额的计算(已知年金现值P,求年金A) (4)㈡即付年金 (5)㈢永续年金 (6)五、名义利率与实际利率的换算 (6)六、项目投资决策评价指标 (6)1.投资利润率 (6)2.静态投资回收期 (7)注:静态与动态投资回收期的区别: (7)3.净现值 (8)4.净现值率 (8)5.获利指数 (9)6.内部收益率 (9)某投资项目预测的净现金流量见下表(万元),设资金基本贴现率为10%,则该项目的净现金值为()万元解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式ii A i A i A i A i A P nnn ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21式中的分式ii n-+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。

递延年金是指在间隔若干期后才开始发生的系列等额收付款项。
以下是一个递延年金的例题及其解答:
例题:假设某公司正在考虑一项将每年支出6000 元的年金,预计未来十年都会支付。
那么此项年金的现值是多少?假设市场的年利率为10%。
解答:
首先,我们需要了解递延年金现值(PA)的计算公式:
PA=A×[(1-(1+i)^(-n))/i]
其中,A 表示年金支出,i 表示折现率,n 表示期数。
根据题目,年金支出 A = 6000 元,折现率i = 10%,期数n = 10 年。
将这些数据代入公式中,我们可以得到:
PA=6000×[(1-(1+0.1)^(-10))/0.1] = 34360.18 元
因此,该递延年金的现值为34360.18 元。


第四节递延年金终值与现值的计算第四节递延年金终值与现值的计算钭志斌丽水职业技术学院一、递延年金递延年金(Deferred Annuity)是指第一次年金收付形式发生在第二期或第二期以后的年金。
递延年金的支付形式如图2-8所示。
12 …mm+1m+2 …m+n递延期递延年金发生的期数二、递延年金终值计算由于递延期m与终值无关只需考虑递延年金发生的期数n。
计算公式如下:12 …mm+1m+2 …m+n递延期递延年金发生的期数【例2-11】农庄的累计净收益为多少?假设江南公司拟一次性投资开发某农庄,预计该农庄能存续15年,但是前5年不会产生净收益,从第6年开始,每年的年末产生净收益5万元。
在考虑资金时间价值的因素下,若农庄的投资报酬率为10%,该农庄给企业带来累计收益为多少?12 …55+15+2 …5+10递延期5递延年金发生的期数10求该农庄给企业带来的累计收益,实际上就是求递延年金终值。
根据=50000×(F/A,10%,10)=50000×153>.937=796850(元)12 …55+15+2 …5+10递延期5递延年金发生的期数10三、递延年金现值的计算递延年金的现值与递延期数相关,递延的期数越长,其现值越低。
递延年金的现值计算有三种方法:方法1:把递延期以后的年金套用普通年金公式求现值,然后再向前折现。
即:12 …mm+1m+2 …m+n递延期递延年金发生的期数方法2:把递延期每期期末都当作有等额的年金收付A,把递延期和以后各期看成是一个普通年金,计算出这个普通年金的现值再把递延期虚增的年金现值减掉即可。
即:12 …mm+1m+2 …m+n假设递延期内每期都有A收付方法3:先求递延年金终值,再折现为现值即12 …mm+1m+2 …m+n【例2-12】农庄的累计投资限额为多少?接例2-11,假设江南公司决定投资开发该农庄,根据其收益情况,该农庄的累计投资限额为多少?实质上,求现值12 …55+15+2 …5+10递延期5递延年金发生的期数10按第一种方法计算:P=50000×(P/A,10%,10)×(P/F,10%,5)=50000×6.1446×0.6209=190759.11(元)按第二种方法计算:P=50000×(P/A,10%,15)-50000×(P/A,10%,5)=50000×7.6061-50000×3.7908=190765.00(元)按第三种方法计算:P=50000×(F/A,10%,10)×(P/F,10%,15)=50000×15.9370×0.2394=190765.89(元)计算结果表明,该农庄的累计投资限额为190759.11元。

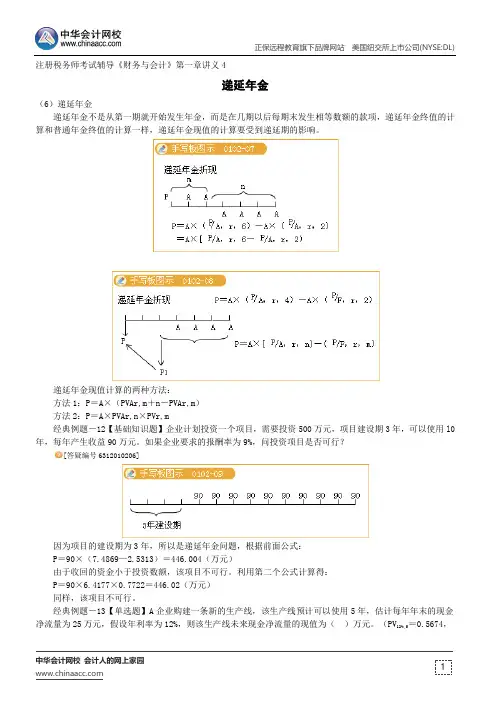
注册税务师考试辅导《财务与会计》第一章讲义4递延年金(6)递延年金递延年金不是从第一期就开始发生年金,而是在几期以后每期末发生相等数额的款项,递延年金终值的计算和普通年金终值的计算一样,递延年金现值的计算要受到递延期的影响。
递延年金现值计算的两种方法:方法1:P=A×(PVAr,m+n-PVAr,m)方法2:P=A×PVAr,n×PVr,m经典例题-12【基础知识题】企业计划投资一个项目,需要投资500万元,项目建设期3年,可以使用l0年,每年产生收益90万元。
如果企业要求的报酬率为9%,问投资项目是否可行?[答疑编号6312010206]因为项目的建设期为3年,所以是递延年金问题,根据前面公式:P=90×(7.4869—2.5313)=446.004(万元)由于收回的资金小于投资数额,该项目不可行。
利用第二个公式计算得:P=90×6.4177×0.7722=446.02(万元)同样,该项目不可行。
经典例题-13【单选题】A企业购建一条新的生产线,该生产线预计可以使用5年,估计每年年末的现金净流量为25万元,假设年利率为12%,则该生产线未来现金净流量的现值为()万元。
(PV12%,5=0.5674,PVA12%,5=3.6048)A.14.185B.90.12C.92D.100[答疑编号6312010207]『正确答案』B『答案解析』未来现金净流量现值=25×PVA 12%,5=25×3.6048=90.12(万元)经典例题-14【单选题】某公司决定分别在2002年、2003年、2004年和2005年的1月1日各存入5 000元,按10%利率,每年复利一次,则2005年1月1日的本利和为()。
(FVA10%,4=4.6410)A.10 000B.15 000C.23 205D.25 205[答疑编号6312010208]『正确答案』C『答案解析』由于下一年初就是上一年末,所以,本题可以理解为从2001年开始,每年年末存入5000元,计算到2004年末的本利和,因此,这道题是期数为4期的普通年金终值的计算问题。
关于递延年⾦在年末付,最终折现的时点是不是第⼀年年末?如果是年初付的形式呢?有什么规律吗?
折现的时点,当然都是现在即时点为0了。
你可以采⽤画数轴的⽅法。
⽐如说,前三年没有现⾦流⼊,后四年:
(1)每年末流⼊1000元,那么画在数轴上就是前三年是空的,后四年每年末流⼊1000元,第⼀步折现1000(P/A,i,4)时点为第四年初即第三年末,再折现到现在是三期折现即1000(P/A,i,4)(P/F,i.3)
(2)每年初流⼊1000元,那么画在数轴上就是前⼆年是空的,从第三年末即第四年初每年末流⼊1000元,第⼀步折现1000(P/A,i,4)时点为第三年初即第⼆年末,再折现到现在是⼆期折现即1000(P/A,i,4)(P/F,i.2)。
你可以按我的讲解在纸上画⼀下。
画完以后你就会明⽩,这样的题画数轴可以“⼀⽬了然”,不易出错。
画数轴是解这类题的⽅法。
递延年金的含义
递延年金是指在最初若干
期没有收付款项的情况下,
后面若干期由等额系列收
付款项的年金形式。
或FV=
【例11】
大宇公司现在从银行借入一笔款项,银行贷款的年利率为7%,借款的偿还方式为从第4年至第10年每年年末偿还本息25万元。
要求:计算这笔借款的数额。
•方法一:
【例11】
大宇公司现在从银行借入一笔款项,银行贷款的年利率为7%,借款的偿还方式为从第4年至第10年每年年末偿还本息25万元。
要求:计算这笔借款的数额。
•方法一:
【例11】
大宇公司现在从银行借入一笔款项,银行贷款的年利率为7%,借款的偿还方式为从第4年至第10年每年年末偿还本息25万元。
要求:计算这笔借款的数额。
•方法二:
【例11】
大宇公司现在从银行借入一笔款项,银行贷款的年利率为7%,借款的偿还方式为从第4年至第10年每年年末偿还本息25万元。
要求:计算这笔借款的数额。
•方法二:
【例11】
大宇公司现在从银行借入一笔款项,银行贷款的年利率为7%,借款的偿还方式为从第4年至第10年每年年末偿还本息25万元。
要求:计算这笔借款的数额。
•方法三:
永续年金是指无限期等额收付的年金,可视为普通年金的特殊形式,即期限
趋于无穷大的普通年金。
永续年金无终值,有现值
递延年金现值的计算
【例12】
如果1股优先股,每年分得股息3元,而年利率是6%。
对于一个准备投资这种股票的人来说,他愿意出多少钱来购买这种优先股?。
一、普通年金 (2)1.普通年金现值公式 (2)二、递延年金 (2)1.递延年金现值公式 (2)三、本例的分析及解答: (3)四、其他年金 (4)㈠普通年金 (4)1.终值公式 (4)2.年偿债基金的计算(已知年金终值,求年金A) (4)3.年资本回收额的计算(已知年金现值P,求年金A) (4)㈡即付年金 (5)㈢永续年金 (6)五、名义利率与实际利率的换算 (6)六、项目投资决策评价指标 (6)1.投资利润率 (6)2.静态投资回收期 (7)注:静态与动态投资回收期的区别: (7)3.净现值 (8)4.净现值率 (8)5.获利指数 (9)6.内部收益率 (9)某投资项目预测的净现金流量见下表(万元),设资金基本贴现率为10%,则该项目的净现金值为()万元解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式ii A i A i A i A i A P nnn ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21式中的分式ii n-+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1)或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式是先计算出n 期的普通年金现值,然后减去前s 期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。
2.例子:某人在年初存入一笔资金,存满5年后每年年末取出1000元,至第10年末取完,银行存款利率为10%。
则此人应在最初一次存入银行的钱数为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=--[])5%,10,/()10%,10,/(1000%10%)101(1%10%)101(11000510A P A P -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=--=1000×(6.1446-3.7908)≈2354(元)或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- )5%,10,/()510%,10,/(10%)101(%)101(110005)510(F P A P i⨯-⨯=+⨯+-⨯=--- =1000×3.7908×0.6209≈2354(元)三、本例的分析及解答:从表中可以看出,现金流量是每年年末的净现金流量,从第2年开始到第10年,每年年末的净现金流量相等,这符合递延年金的定义,那么从第2年到第10年的每年年末的净现金流量的现值要按递延年金来计算。
第0年的年末净现金流量为-500,说明是第1年年初一次性投入500万元,第1年年末的净现金流量为60万元,按复利现值的公式来计算。
从本例中,建设期为0年,经营期为10年,年利率为10%,那么本例的投资的净现值计算为:∑∑=-=++-+=nt t tmt n t t R P R N NPV 111)1()1( 500%)101(%)101(1100%)101(601)110(1-+⨯+-⨯++⨯=----i500)1%,10,/()110%,10,/(100)1%,10,/(60-⨯-⨯+⨯=F P A P F P =60×0.9091+100×5.7590×0.9091-500= 578.09669-500≈78.09669(万元)四、其他年金㈠普通年金 1.终值公式ii A F n 1)1(-+⋅=式中的分式ii n 1)1(-+称作“年金终值系数”,记作为(F/A ,i ,n ),可通过直接查阅“1元年金终值表”求得有关的数值,上式也可写作:F=A (F/A ,i ,n )例:假设某项目在5年建设期内每年年末从银行垡100万元,借款年利率为10%,则该项目竣工时就付本息的总额为:%101%)101(1005-+⨯=F =100×(F/A ,10%,5)=100×6.1051=610.51(万元)2.年偿债基金的计算(已知年金终值,求年金A )偿债基金是指为了在约定的未来某一时点清偿某笔债务或者积聚一定数额的资金而必须分次等额形成的存款准备金。
它的计算实际上是年金终值的逆运算。
1)1(-+⋅=n i iF A式中的分式1)1(-+n i i称作“偿债基金系数”,记为(A/F ,i ,n ),可通过直接查阅“偿债基金系统表”或通过年金终值系数的倒数推算出来,上式也可写作:A=F (A/F ,i ,n )或者A=F[1/(F/A ,i ,n )]例:假设某企业有一笔4年后到期的借款,到期值为1000万元。
若存款年复利率为10%,则为偿还该借款应建立的偿债基金应为:1%)101(%1010004-+⨯=A =1000×0.2154=215.4(万元) 或A=1000×[1/(F/A ,10%,4)]=1000×(1/4.6410)=215.4(万元)3.年资本回收额的计算(已知年金现值P ,求年金A )ni iP A -+-⨯=)1(1式中的分式ni i-+-)1(1称作“资本回收系数”记为记为(A/P ,i ,n ),可通过直接查阅“资本回收系统表”或通过年金现值系数的倒数推算出来,上式也可写作:A=P (A/P ,i ,n )或者A=P[1/(P/A ,i ,n )]例:某企业现在借得1000万元的贷款,在10年内以年利率12%等额偿还,则每年应付的金额为:10%)121(1%121000-+-⨯=A =1000×0.1770=177(万元) 或 A=1000×[1/(P/A ,12%,10)]=1000×(1/5.6502)=177(万元)㈡即付年金即付年金,是指从第一期起,在一定时期内每期期初等额收付的系列款项,又称先付年金,它与普通年金的区别仅在于付款时间的不同。
1.由于付款时间的不同,n 期即付年金终值比n 期普通年金的终值多计算一期利息。
因此,在n 期普通年金终值的基础上乘上(1+i)就是n 期即付年金的终值。
⎥⎦⎤⎢⎣⎡--+⨯=+-+⨯=+11)1()1(1)1(1i i A i i i A F n n式中11)1(1--++ii n 称作“即付年金终值系数”,它是在普通年金终值系数的基础上,期数加1,系数值减1所得的结果。
通常记为[(F/A ,i ,n+1)-1],这样,通过查阅“一元年金终值表”得到n+1期的值,然后减去1便可得对应的即付年金终值系数的值。
上式也可写作:F=A[(F/A ,i ,n+1)-1]例:某公司决定连续5年于每年年初存入100万元作为住房基金,银行存款利率为10%。
则该公司在第5年末能一次取出本利和为:F= A[(F/A ,i ,n+1)-1]=100×[(F/A ,10%,5+1)-1] =100×(7.7156-1)=672(万元)2.由于付款时间的不同,n 期即付年金现值比n 期普通年金的现值少折现一期。
因此,在n 期普通年金现值的基础上乘上(1+i)就是n 期即付年金的现值。
⎥⎦⎤⎢⎣⎡++-⨯=+⨯+-⨯=---1)1(1)1()1(1)1(i i A i i i A P n n式中⎥⎦⎤⎢⎣⎡++---1)1(1)1(i i n 称作“即付年金现值系数”,它是在普通年金现值系数的基础上,期数减1,系数值加1所得的结果。
通常记为[(P/A ,i ,n-1)+1],这样,通过查阅“一元年金现值表”得到n-1期的值,然后加上1便可得对应的即付年金现值系数的值。
上式也可写作:P=A[(P/A ,i ,n-1)+1]㈢永续年金永续年金,是指无限期等额收付的特种年金,可视为普通年金的特殊形式,即期限趋于无穷的普通年金。
存本取息可视为永续年金的例子。
也可将利率较高、持续期限较长的年金视同永续年金。
由于永续年金持续期无限,没有终止时间,因此没有终值,只有现值。
公式为:i Ai A P t t=+⨯=∑∞=1)1(1 例:某人持有的某公司优先股,每年每股股利为2元,若此人想长期持有,在利率为10%的情况下,请对该股票投资进行估价。
这是一个求永续年金现值的问题,即假设该优先股每年股利固定且持续较长时期,计算出这些股利的现值之和,即为该股票的估价。
P=A/i=2/10%=20(元)五、名义利率与实际利率的换算当每年复利次数超过一次时,这样的年利率叫做名义利率,而每年只复利一次的利率才是实际利率。
公式:i=(1+r/m)m -1式中:i 为实际利率,r 为名义利率,m 为每年复利次数。
例:某企业于年初存入10万元,在年利率为10%,半年复利一次的情况下,到第10年末,该企业能得到多少本利和?依题意,P=10,r=10%,m=2,n=10则:i=(1+r/m)m -1= i=(1+10%/2)2-1=10.25% F=P(1+i)n =10×(1+10.25%)10=26.53(万元)这种方法的缺点是调整后的实际利率往往带有小数点,不便于查表。
可以把利率变为r/m ,期数相应变为m ×n ,则有:F=P(1+r/m) m ×n =10×(1+10%/2)20=10×(F/P,5%,20)=26.53(万元)六、项目投资决策评价指标1.投资利润率投资利润率又称投资报酬率(记作ROI),是指达产期正常年度利润或年均利润占投资总额的百分比。