递延年金及插值法练习题
- 格式:doc
- 大小:21.50 KB
- 文档页数:1

财务管理年金类混合型练习题篇一:财务管理预付年金练习题财务管理预付年金练习题普通年金1元、利率为i,经过n期的年金现值,记作,可查年金现值系数表. 推导出普通年金终值、现值的一般计算公式普通年金终值指一定时期内,每期期末等额收入或支出的本利和,也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值.例如:每年存款1元,年利率为10%,经过5年,逐年的终值和年金终值,可计算如下:1元1年的终值=1.000元1元2年的终值=1=1.1001元3年的终值=2=1.2101元4年的终值=3=1.3311元5年的终值=4=1.4641元年金5年的终值=6.105如果年金的期数很多,用上述方法计算终值显然相当繁琐.由于每年支付额相等,折算终值的系数又是有规律的,所以,可找出简便的计算方法.设每年的支付金额为A,利率为i,期数为n,则按复利计算的年金终值S为:S=A+A×+?+A×n-1,等式两边同乘以:S=A+A2+?+An,(n等均为次方)(2)上式两边相减可得:S-S=An-A,S=A[(1+i)n-1]/i式中[(1+i)n-1]/i的为普通年金、利率为i,经过n期的年金终值记作,可查普通年金终值系数表.年金现值通常为每年投资收益的现值总和,它是一定时间内每期期末收付款项的复利现值之和.每年取得收益1元,年利率为10%,为期5年,上例逐年的现值和年金现值,可计算如下:1年1元的现值==0.9092年1元的现值==0.8263年1元的现值==0.7514年1元的现值==0.6835年1元的现值==0.6211元年金5年的现值=3.790预付年金现值公式:预付年金现值计算是在普通年金现值计算的基础上,期数减1,系数加1 。
计算公式为:P=A×{【 [1-(1+i)-(n-1)]/i +1】},可以简化记为{(P/A,i,n-1)+1}预付年金也称先付年金、即付年金,它是在每期期初等额的系列收款、付款的年金。

财务管理插值法例题插值法在财务管理中有着广泛的应用,它可以帮助我们估计在某个特定区间内的未知数值。
插值法基于一个简单的理念:如果已知一个函数在几个点上的值,那么我们可以通过这些点之间的插值来估算该函数在其他点的值。
一、常见的插值方法1.线性插值:它是插值方法中最简单的一种,假设两个已知点之间的函数为直线,根据这个直线方程来估算未知点的值。
2.多项式插值:它假设函数在已知点之间存在一个多项式,通过这个多项式来估算未知点的值。
二、插值法在财务管理中的应用插值法在财务管理中有着广泛的应用,例如:1.估算违约风险:在债券或贷款的违约风险分析中,我们可以通过插值法来估算违约发生概率。
2.预测利率:在债券定价或货币时间价值计算中,我们可以通过插值法来预测未来的利率。
3.估算收益率:在投资项目的评估中,我们可以通过插值法来估算未来的收益率。
三、30道财务管理插值法例题与答案例题1:某公司发行了一笔面值为1000元的债券,票面利率为5%,债券期限为10年。
假设市场利率为4%,请问该债券的发行价格应该是多少?答案:首先,我们可以使用插值法来计算债券的发行价格。
假设债券的发行价格为P,根据债券定价公式:PV=C/(1+r)^t,其中C为每年的利息支付,r为市场利率,t为债券期限。
已知C=50(因为票面利率为5%),r=4%(即0.04),t=10年,代入公式可得:PV=50/(1+0.04)^10≈737.94元。
因此,该债券的发行价格应该是737.94元。
例题2:某公司预计未来三年的现金流分别为100万元、150万元和200万元,假设年利率为10%,请问未来三年的现金流现值分别是多少?答案:使用插值法计算现金流的现值。
已知现金流和利率,我们可以使用公式PV=C/(1+r)^t来计算每个现金流的现值。
对于第一年的现金流,我们有C=100万元,r=10%(即0.1),t=1年,代入公式可得:PV=100/(1+0.1)^1≈90.91万元;对于第二年的现金流,我们有C=150万元,r=10%,t=2年,代入公式可得:PV=150/(1+0.1)^2≈138.63万元;对于第三年的现金流,我们有C=200万元,r=10%,t=3年,代入公式可得:PV=200/(1+0.1)^3≈223.6万元。

一、普通年金 (2)1.普通年金现值公式 (2)二、递延年金 (2)1.递延年金现值公式 (2)三、本例的分析及解答: (3)四、其他年金 (4)㈠普通年金 (4)1.终值公式 (4)2.年偿债基金的计算(已知年金终值,求年金A) (4)3.年资本回收额的计算(已知年金现值P,求年金A) (4)㈡即付年金 (5)㈢永续年金 (6)五、名义利率与实际利率的换算 (6)六、项目投资决策评价指标 (6)1.投资利润率 (6)2.静态投资回收期 (7)注:静态与动态投资回收期的区别: (7)3.净现值 (8)4.净现值率 (8)5.获利指数 (9)6.内部收益率 (9)某投资项目预测的净现金流量见下表(万元),设资金基本贴现率为10%,则该项目的净现金值为()万元解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
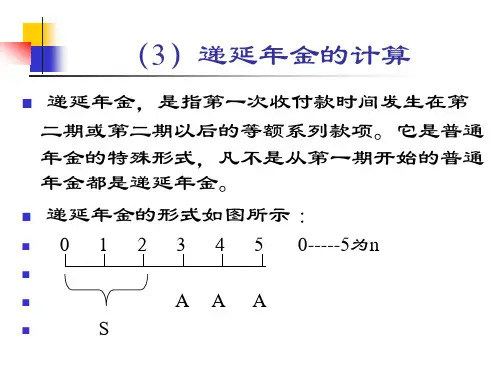
1.普通年金现值公式ii A i A i A i A i A P nnn ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21式中的分式ii n-+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。

年金确定练习题一、单利年金问题1. 假设你存入一笔本金为P的金额,年利率为r,存期为n年。
计算单利年金A的公式是:A = P(1 + rn)2. 问题1:假如你存入10000元,年利率为5%,存期为10年,计算这笔单利年金的总额。
解:代入公式计算,A = 10000(1 + 0.05 * 10) = 15000元3. 问题2:现在你每年存入5000元,年利率为8%,存期为5年。
计算这笔单利年金的总额。
解:考虑每年存入的金额,我们可以将问题分解为5个单利年金之和。
首先,计算第1年存入的5000元在第5年的总额: A1 = 5000 * (1 + 0.08 * 5) = 7000元同理,计算第2年存入的5000元在第5年的总额:A2 = 5000 * (1 + 0.08 * 4) = 5800元...最后计算总金额为:A = A1 + A2 + A3 + A4 + A5 = 7000 + 5800 + 4600 + 3400 + 2200 = 23000元1. 复利年金是指在每个计息周期结束时,将利息累积到本金中,下一个计息周期将基于新的本利和进行计算。
2. 复利年金的计算公式是:A = P(1 + r)^n3. 问题3:假设你存入10000元,年利率为5%,存期为10年,计算这笔复利年金的总额。
解:代入公式计算,A = 10000(1 + 0.05)^10 = 16288.95元4. 问题4:现在你每年存入5000元,年利率为8%,存期为5年。
计算这笔复利年金的总额。
解:同样,我们可以将问题分解为5个复利年金之和。
首先,计算第1年存入的金额在第5年的总额:A1 = 5000 * (1 + 0.08)^5 = 7346.85元计算第2年存入的金额在第5年的总额:A2 = 5000 * (1 + 0.08)^4 = 6771.36元...最后计算总金额为:A = A1 + A2 + A3 + A4 + A5 = 7346.85 + 6771.36 + 6235.85 + 5731.16 + 5263.47 = 31348.69元1. 递延年金是指在一定条件下,年金的支付或支出推迟到未来的某一时点开始。


【例1·单选题】已知(F/A,10%,9)=13.579,(F/A,10%,11)=18.531。
则10年,利率10%的预付年金终值系数为( A )。
A.17.531B.15.937C.14.579D.12.579【解析】预付年金终值系数与普通年金终值系数相比期数加1,系数减1,所以10年,10%的预付年金终值系数=18.531-1=17.531【例2·计算题】某人拟购房,开发商提出两种方案,一是5年后一次性付120万元,另一方案是从现在起每年年初付20万元,连续5年,若目前的银行存款利率是7%,应如何付款?【答案】方案1终值:F1=120万元方案2的终值:F2=20×(F/A,7%,5)×(1+7%)=123.065(万元)或 F2=20×(F/A,7%,6)-20=123.066(万元)所以应选择5年后一次性付120万元。
【例3·计算题】某人拟购房,开发商提出两种方案,一是现在一次性付80万元,另一方案是从现在起每年年初付20万元,连续支付5年,若目前的银行贷款利率是7%,应如何付款?【答案】方案1现值:P1=80万元方案2的现值:P2=20×(P/A,7%,5)×(1+7%)=87.744(万元)或 P2=20+20×(P/A,7%,4)=87.744(万元)应选择现在一次性付80万元。
【例4·单选题】有一项年金,前3年无流入,后5年每年年初流入500万元,假设年利率为10%,其现值为(B)万元。
A.1994.59B.1565.68C.1813.48D.1423.21【解析】本题是递延年金现值计算的问题,对于递延年金现值计算关键是确定正确的递延期。
本题总的期限为8年,由于后5年每年年初有流量,即在第4~8年的每年年初也就是第3~7年的每年年末有流量,从图中可以看出与普通年金相比,少了第1年末和第2年末的两期A,所以递延期为2,因此现值=500×(P/A,10%,5)×(P/F,10%,2)=500×3.791×0.826=1565.68(万元)。

第四章资金时间价值练习题一、填空1、年金的特点是()和()。
2、利息的种类有()和()两种。
3、请用式子来描述名义利率与实际利率之间的关系()4、某人最近在保险公司申请到某特种保险,保险单上规定,该投保人从第11年开始至第20年止,每年年初可收到保险公司的保险金1000元。
假定在这20年内,利率均为10%,问此人此次投保可获保险金的总现值为( )5、影响资金等值的三因素:()()()。
6、(F/P,6%,9)=1.689,(F/P,7%,9)=1.838,当(F/P,I,9)=1.750 则I为()二、判断题1、在利率和计息期数相同的条件下,复利现值系数与复利终值系数互为倒数;年金现值系数与年金终值系数互为倒数。
()2、在本金和利率相同的情况下,若只有一个计息期,单利终值与复利终值是相同的。
()3、复利现值就是为在未来一定时期获得一定的本利和而现在所需的年金。
()4、终值就是本金和利息之和()5、凡一定时期内,每期均有付款的现金流量都属于年金()6、在现值和利率一定的情况下,计息期数越多,则复利终值越小()7、现在1000元与将来1000元数值相等,其内在经济价值也相等。
()8、永续年金无终值()9、递延年金的终值大小与递延期无关()10、不同时间点上的货币收支可直接进行比较()11、单利和复利是两种不同的计息方法,因此单利终值和复利终值在任何情况下都不可能相同。
()三、单选题1.6年分期付款购物,每年年初付款500元,设银行利率为10%,该项分期付款相当于现在一次现金支付的购价是()。
A.2395.50元B.1895.50元C.1934.50元D.2177.50元2.有一项年金,前3年年初无流入,后5年每年年初流入500万元,假设年利率为10%,其现值为( )。
A.1994.59B.1565.68C.1813.48D.1423.213、甲某拟存入一笔资金以备三年后使用。
假定银行三年期存款年利率为5%,甲某三年后需用的资金总额为34 500元,则在单利计息情况下,目前需存人的资金为()元。

递延年金终值计算例题
递延年金是一种金融工具,它可帮助人们获得收益,将资金保值和增值,它结合了投资和保险功能。
有时,它也可以被称为增值保障金或增值保险。
在具体的案例中,假设有一位客户手头有一笔5000元的资金,此人希望将此款项存入递延年金,款项受到保护,以便在未来十年内取回,以便获得收益。
在存入资金之前,有必要首先确定递延年金的最终价值。
“最终价值”指的是在到期日期之后取回资金后,资金金额较原先增长了多少。
为了计算最终价值,需要使用下面的公式:
最终价值=原始金额×1+票息率×期数
例如,假设本次客户存入的是5000元,存期是十年,年票息率是5%,则此次客户存款最终价值将为:
最终价值=5000元×1+5%×10=7500元
因此,十年后,本次客户取回的资金将为7500元。
递延年金是一种很好的投资工具,它可以提供安全的环境,让本金和收益受到保护。
但是,在投资递延年金之前,投资者应密切关注投资项目的收益率、期限和费用,以便确定收益是否达到期望水平,避免最终造成损失。
总的来说,递延年金是一种可以获得收益,并保护本金的投资工具。
它有助于投资者理解投资项目,让他们能够准确估算他们最终收益。
但是,一定要认真研究项目的细节,以确保收益的安全性和可靠
性。

1、已知 f (x )=ln x 的数值表如下,分别用线性及二次 Lagrange 插值法计算f (0.54) 的近似值,并估计误差。
解:(1)线性插值法:因为()ln f x x = 时递增函数,所以取0.5和0.6为插值节点。
则线性插值多项式为:0011()()()()f x F x f l x f l x ==+0.540.60.540.5(0.54)(0.54)(0.5)(0.6)0.50.60.60.50.6930.6(0.510)0.40.6198f F f f --≈=+-- =-⨯+-⨯=-截断误差:101011()''()()(),(,)2R x f x x x x x x ξξ=--∈ 121(0.54)0.0012R ξ=11(0.5,0.6)110.0012(0.54)0.00120.360.25,0.0032(0.54)0.0048R R ξ∈∴⨯<<⨯<<即 (2)二次lagrange 插值法:A :若取0.4,0.5和0.6为插值点,0120.916,0.693,0.510f f f =-=-=-012(0.540.5)(0.540.6)0.12(0.40.5)(0.40.6)(0.540.4)(0.540.6)0.84(0.50.4)(0.50.6)(0.540.4)(0.540.5)0.28(0.60.4)(0.60.5)l l l --==-----==----==--001122(0.54)(0.54)(0.54)(0.54)(0.54)0.615f F f l f l f l ≈=++=-截断误差:20121()'''()()()()3!R x f x x x x x x ξ=---则231(0.54)0.000112R ξ=333233[0.4,0.6],()111,0.60.4110.000112(0.54)0.0001120.40.6f x R ξξ∈∴<<-⨯<<-⨯递增;即20.00175(0.54)0.000519R -<<-B :若取0.5,0.6和0.7为插值点,0120.693,0.510,0.357f f f =-=-=-012(0.540.6)(0.540.7)0.48(0.50.6)(0.50.7)(0.540.5)(0.540.7)0.64(0.60.5)(0.60.7)(0.540.5)(0.540.6)0.12(0.70.5)(0.70.6)l l l --==----==----==---001122(0.54)(0.54)(0.54)(0.54)(0.54)0.6162f F f l f l f l ≈=++=-截断误差:20121()'''()()()()3!R x f x x x x x x ξ=--- 则231(0.54)0.000128R ξ=333233[0.5,0.7],()111,0.70.5110.000128(0.54)0.0001280.70.5f x R ξξ∈∴<<⨯<<⨯递增;即20.000373(0.54)0.001024R <<2、已知f(x)=e -x 的一组数据见下表,用抛物插值法计算e -2.1的近似值。

财务管理年金类混合型练习题篇一:财务管理预付年金练习题财务管理预付年金练习题普通年金1元、利率为i,经过n期的年金现值,记作,可查年金现值系数表. 推导出普通年金终值、现值的一般计算公式普通年金终值指一定时期内,每期期末等额收入或支出的本利和,也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值.例如:每年存款1元,年利率为10%,经过5年,逐年的终值和年金终值,可计算如下:1元1年的终值=1.000元1元2年的终值=1=1.1001元3年的终值=2=1.2101元4年的终值=3=1.3311元5年的终值=4=1.4641元年金5年的终值=6.105如果年金的期数很多,用上述方法计算终值显然相当繁琐.由于每年支付额相等,折算终值的系数又是有规律的,所以,可找出简便的计算方法.设每年的支付金额为A,利率为i,期数为n,则按复利计算的年金终值S为:S=A+A×+?+A×n-1,等式两边同乘以:S=A+A2+?+An,(n等均为次方)(2)上式两边相减可得:S-S=An-A,S=A[(1+i)n-1]/i式中[(1+i)n-1]/i的为普通年金、利率为i,经过n期的年金终值记作,可查普通年金终值系数表.年金现值通常为每年投资收益的现值总和,它是一定时间内每期期末收付款项的复利现值之和.每年取得收益1元,年利率为10%,为期5年,上例逐年的现值和年金现值,可计算如下:1年1元的现值==0.9092年1元的现值==0.8263年1元的现值==0.7514年1元的现值==0.6835年1元的现值==0.6211元年金5年的现值=3.790预付年金现值公式:预付年金现值计算是在普通年金现值计算的基础上,期数减1,系数加1 。
计算公式为:P=A×{【 [1-(1+i)-(n-1)]/i +1】},可以简化记为{(P/A,i,n-1)+1}预付年金也称先付年金、即付年金,它是在每期期初等额的系列收款、付款的年金。
第二章时间价值、风险与报酬、估价一、单项选择题1、某公司拟于5年后一次还清所欠债务100000元,假定银行利息率为10%,5年10%的年金终值系数为6.1051,5年10%的年金现值系数为3.7908,则应从现在起每年末等额存入银行的偿债基金为(A )。
A.16379.75B.26379.66C.379080D.610510[解析]本题属于已知终值求年金,故答案为:A=S/(S/A,10%,5)=100000/6.1051=16379.75(元)2、某公司向银行借入23000元,借款期为9年,每年的还本付息额为4600元,则借款利率为(B )A.16.53%B.13.72%C.17.68%D.18.25%[解析]本题的考点是利用插补法求利息率。
3、一项1000万元的借款,借款期3年,年利率为5%,若每年半年复利一次,年有效年利率会高出名义利率(C )。
A.0.16%B.0.25% C. 0.06% D. 0.05%[解析]已知:M = 2,r = 5%根据有效年利率和名义利率之间关系式:=(1+5%/2)2-1= 5.06 %有效年利率高出名义利率0.06%(5.06%-5%)。
4、某企业于年初存入银行10000元,假定年利息率为12%,每年复利两次.已知(F/P,6%,5)=1.3382,(F/P,6%,10)=1.7908,(F/P,12%,5)=1.7623,(F/P,12%,10)=3.1058,则第5年末的本利和为(C )元。
A. 13382B. 17623C. 17908D. 31058[解析]第5年末的本利和=10000×(S/P,6%,10)=17908(元)。
5、下列因素引起的风险中,投资者可以通过证券投资组合予以消减的是(D)。
A.宏观经济状况变化B.世界能源状况变化C.发生经济危机D.被投资企业出现经营失误6、下列各项中,不能通过证券组合分散的风险是(D )。
A.非系统性风险B.公司特别风险C.可分散风险D.市场风险7、假定某企业的权益资金与负债资金的比例为60:40,据此可断定该企业(D )A.只存在经营风险B.经营风险大于财务风险C.经营风险小于财务风险D.同时存在经营风险和财务风险8、在没有通货膨胀的条件下,纯利率是指(T )。
1.永续年金:假如有一笔永续年金,每年要付给投资者100美元,如果贴现率为8%,该永续年金的现值为多少?PV=Cr=1000.08=1,250美元解答:2.永续增长年金:假如有一个房屋建筑在扣除各项费用后,明年房东会有100,000美元的房租现金收入。
这笔现金流预计会以每年5%的速度增长。
如果能肯定这种增长趋势会永远持续下去,这种现金流序列就称作永续增长年金。
贴现率为11%,这笔现金流的现值为多少?解答:PV=Cr-g=100,0000.11-0.05=1,666,667美元3.普通年金:某人赢得了博彩大奖,在以后的20年中每年将得到50000美元的奖金,一年以后开始领取奖金。
博采公司的广告称这是一个百万美元的大奖,因为1,000,000美元=50,000美元x 20,若年利率为8%,这项奖项的真实价值是多少?解答:PV=C1r-1r(1+r)Téëêùûú=C·A r T=50,000´A0.0820=50,000´9.8181=490,9054.递延年金:某人在六年后开始的四年之内,每年会收到500美元。
如果利率为10%,那么他的年金现值为多少?解答:分析过程包括两步:(1)0 1 2 3 4 5 6 7 8 9500 500 500 500 在第5期的年金的现值为:PV=C1r-1r(1+r)Téëêùûú=C·A r T=500´A0.104=500´3.1699=1,584.95美元经常会有学生认为1,584.95美元是在第6期的现值,因为年金是在第6期开始的。
但是,我们的计算公式求出的是年金在开始付出现金流之前一期的现值。
在普通年金的案例中,年金的第一次支付是发生在第一期的,而递延年金的第一次支付是发生在后面的某一期,因此在考虑的时候可以将第5期看作0时点,然后可将递延年金看作一个普通年金,但是算出第5期年金现值之后,必须要贴现。
资金时间价值练习题及答案一、单项选择题1.资金时间价值与利率之间的关系是(A)。
A.交叉关系B.被包含与包含关系C.主次关系D.没有任何关系2.6年分期付款购物,每年初付200元,设银行利率为10%,该项分期付款相当于一次现金支付的购价是(A)。
A.958.20元B.758.20元C.1200元D.354.32元3.关于递延年金,下列说法中不正确的是(A)。
A.递延年金无终值,只有现值B.递延年金终值计算方法与普通年金终值计算方法相同C.递延年金终值大小与递延期无关D.递延年金的第一次支付是发生在若干期以后的4.已知(F/A,10%,5)=6.1051,那么,i=10%,n=5时的偿债基金系数为(D)。
A.1.6106B.0.6209C.0.2638D.0.16385.某一投资项目,投资5年,每年复利四次,其实际年利率为8.24%,则其名义利率为(A)。
A.8%B.8.16%C.8.04%D.8.06%6.在期望收益不相同的情况下,标准差越大的项目,其风险(A)。
A.越大B.越小C.不变D.不确定7.如果(P/A,5%,5)=4.3297,则(A/P,5%,5)的值为(A)投资收回。
A.0.2310B.0.7835C.1.2763D.4.32978.普通年金现值系数的倒数称为(D)。
A.普通年金终值系数B.复利终值系数C.偿债基金系数D.投资回收系数9.关于标准离差和标准离差率,下列描述正确的是:()A.标准离差是各种可能报酬率偏离期望报酬率的平均值B.如果选择投资方案,应以标准离差为评价指标,标准离差最小的方案为最优方案C.标准离差率即风险报酬率D.对比期望报酬率不同的各项投资的风险程序,应用标准离差同期望报酬率的比值,即标准离差率10.11.有一项年金,前3年无流入,后5年每年年初流入500元,年利率为10%则其现值为(B)元。
A.1994.59B.1565.68C.1813.48D.1423.2112.甲方案的标准离差是2.11,乙方案的标准离差是2.14,如甲、乙两方案的期望值相同,则甲方案的风险()乙方案的风险。