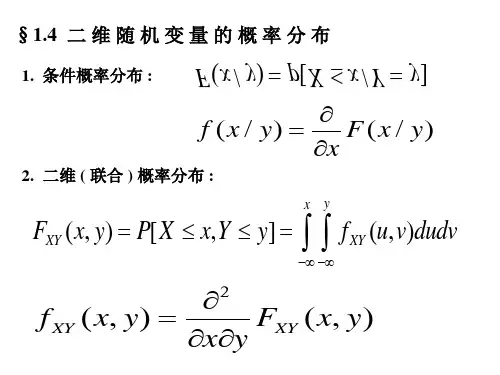- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阅读课文(自学例1然后思考1)
思考一: 一个袋中装有 2 个黑球和 3 个白球,如果不放 回地抽取两个黑球, 记事件 “第一次抽到黑球” 为 A; 事件“第二次抽到黑球”为 B. ⑴分别求事件 A、B、AB 发生的概率; ⑵求 P ( B | A) 练习1. 掷两颗均匀骰子,已知第一颗掷出6点,问“掷 出点数之和不小于10”的概率是多少?
难题签而乙抽到难题签,4)甲,乙,丙都抽到难题签
的概率。 解 设A,B,C分别表示“甲、乙、丙抽到难签”
4 则 P (1) P ( A) 10 6 4 P (3) P ( AB ) 10 9
4 3 P (2) P ( AB ) 10 9 4 3 2 P (4) P( ABC ) 10 9 8
即平均1000个具有阳性反应的人中大约只有87人患有癌症.
2.某种动物出生之后活到20岁的概率为0.7,活到25岁的 概率为0.56,求现年为20岁的这种动物活到25岁的概率.
解 设A表示“活到20岁”(即≥20),B表示 “活到25岁” (即≥25) 则 P( A) 0.7, P( B) 0.56 所求概率为
1.条件概率 P ( B A) P ( AB ) P ( A)
2.概率 P(B|A)与P(AB)的区别与联系
P( AB) 表示在样本空间 中, 计算 AB发生
的概率, 而 P(B A ) 表示在缩小的样本空间 A 中, 计算 B 发生的概率.用古典概率公式, 则 AB 中样本点数 P( B A ) , A 中样本点数 作业: AB 中样本点数 P( AB) 课本 中样本点数 一般来说, P(B A ) 比 P( AB) 大.
P ( AB ) 在刚才问题中, 我们发现 P ( B | A) . P ( A) 一般化: 定义:一般地 , 设 A,B 为两个事件 , 且 P( A) 0 , 称
P ( AB ) 为在事件 A 发生的条件下, 事件 B P ( B | A) P ( A) 发生的条件概率 .
注:⑴ 0 ≤ P ( B | A) ≤1 ; A AB B ⑵几何解释 : ⑶可加性: 如果 B和C 互斥, 那么 P ( B C ) | A P( B | A) P(C | A)
解:∵事件 A 发生的条件下,事件 B 的概 率即P(B|A)
A B 都发生,但样本空 间缩小到只包含A的样本点 n( AB) 2 P( B | A) n( A) 3
5
B
1 3 4,6
A
2
练习5.考虑恰有两个小孩的家庭.若已知某一家有男孩, 求这家有两个男孩的概率;若已知某家第一个是男孩, 求这家有两个男孩(相当于第二个也是男孩)的概率. (假定生男生女为等可能)
条件概率
引入
引入问题
条件概率 及思考一 本课小结
思考二
作业:课本 P A 组第 2 题 68
条件概率
我们知道求事件的概率有加法公式: 若事件 A 与 B 互斥,则 P( A B) P( A) P( B) . 那么怎么求 A 与 B 的积事件 AB 呢?
注: 1.事件 A 与 B 至少有一个发生的事件叫做 A 与 B 的和事件,记为 A B ( 或 A B ); 2.事件 A 与 B 都发生的事件叫做 A 与 B 的积事件, 记为 A B (或 AB ); 3.若 AB 为不可能事件,则说事件 A 与 B 互斥.
P( A | B) 45%
于是 所以
P( B ) 4%
P( B) 1 P( B ) 96%
P( A) P( AB) P( B) P( A | B)
96% 45% 43.2%
练习4 练习5
练习4:抛掷一颗骰子,观察出现的点数
B={出现的点数是奇数}={1,3,5} A={出现的点数不超过3}={1,2,3} 若已知出现的点数不超过3,求出现的点数是奇数的概率
2.某种动物出生之后活到20岁的概率为0.7,活到25岁的
概率为0.56,求现年为20岁的这种动物活到25岁的概率.
作业:课本 P A 组第 2 题 68
,某 种 诊 断 癌 症 的 试 1. 根 据 以 往 的 临 床 记 录 验具有如下的效果 :若以A 表示事件 "试 验 反 应 为阳性 " ,以 C 表 示 事 件 "被 诊 断 者 患 有 癌 症 ",则 有 P ( A C ) 0.95, P ( A C ) 0.95.现 在 对 自 然 人 群 进行普查 ,设 被 试 验 的 人 患 有 癌的 症概 率 为 0.005, 即 P (C ) 0.005, 试 求 P (C A).
解: 设A={掷出点数之和不小于10},B={第 一颗掷出6点} 3 n( AB ) 1 36 P( A | B) n( B ) 6 2
36
练习2
练习2. 一盒子装有4 只产品,其中有3 只一等品,1只二 等品.从中取产品两次,每次任取一只,作不放回抽样.设 事件A为“第一次取到的是一等品” ,事件B 为“第二 次取到的是一等品”,试求条件概率P(B|A). 解 将产品编号, 1, 2, 3 为一等品; 4 号为二等品. 以 ( i , j ) 表示第一次、 第二次分别取到第i 号、 第
P( AB) P( B) P( B A) 0.8 P( A) P( A)
B
5
0.560.7Fra bibliotekA3.甲,乙,丙3人参加面试抽签,每人的试题通过不放 回抽签的方式确定。假设被抽的10个试题签中有4个是 难题签,按甲先,乙次,丙最后的次序抽签。试求1)
甲抽到难题签,2)甲和乙都抽到难题签,3)甲没抽到
解 P ( A C ) 0.95, P ( A C ) 1 P ( AC ) 0.05,
P (C ) P ( A C ) P ( C ) P ( A C ) P (C ) P ( A C )
P(C ) 0.005, P(C ) 0.995,
P ( C A) 0.087.
j 号产品, 则试验的样本空间为 {(1,2), (1,3), (1,4), (2,1),(2,3),(2,4) ,,(4,1),(4,2),(4,3)},
A {(1, 2),(1, 3),(1,4),(2,1),(2, 3),(2,4),(3,1),(3, 2),(3,4)}, AB {(1,2), (1,3), ( 2,1), ( 2,3), ( 3,1), ( 3,2)}, 由条件概率的公式得 P ( B A) n( AB ) 6 12 2 . 9 12 3 n( A)
首先看一个抓阄的问题: 三个阄, 其中一个阄内写着“奖”字, 两个阄 内不写字 , 三人依次抓取,问各人抓到“奖”字阄的 概率是否相同?
解:记 Ai 表示:“第一人抓到有奖字” 的事件,i 1, 2, 3 1 21 1 2 1 1 1 , P ( A3 ) 则有 P ( A1 ) , P ( A2 ) 3 3 2 3 3 21 3 三人抓到“奖”字阄的概率是相同的. 思考:(接上题 )如果已经知道第一个人没有抓到“奖” 字,那么最后一名同学抓到“奖”字的概率又是多少? 不妨记所求概率为 P ( B | A) .由古典概型的知识, n( AB ) 1 不难求得概率为 P ( B | A) n( A) 2
4.全年级100名学生中,有男生(以事件A表示)80人, 女生20人; 来自北京的(以事件B表示)有20人,其中 男生12人,女生8人;免修英语的(以事件C表示)40 人中,有32名男生,8名女生。求
P( A), P( B), P( A B), P( B A), P ( AB ),
80 100 20 100 12 20 12 80 12 100
练习3
练习3 .一个盒子中有6只白球、4只黑球,从中不放 回地每次任取1只,连取2次,求 (1) 第一次取得白 球的概率; (2) 第一、第二次都取得白球的概率; (3) 第一次取得黑球而第二次取得白球的概率.
解
设A表示第一次取得白球, B表示第二次取得白球, 则 6 (1) P ( A) 0.6 10
解
Ω={ (男, 男) , (男 , 女) , (女 , 男) , (女 , 女) } A={(男, 男) },
设 B= “有男孩” , 则 B={(男, 男) , (男 , 女) , (女 , 男) } A= “有两个男孩” ,
3 于是得 P B 4
P B1 1 2
B1 =“第一个是男孩”
P BA 1 1 P BA P A P A | B P ( B) 3 4
1 4
B1 ={(男, 男) , (男 , 女) }
P B1 A 1 P A | B1 P( B1 ) 2
P B1 A P A
学习小结:
P(C ), P(C A), P( A B ), P( AC )
40 100 32 80 12 80 32 100
6 5 (2)P ( AB ) P( A) P( B A) 0.33 10 9 4 6 (3)P ( AB ) P ( A) P ( B A) 0.27 10 9
思考二.一批产品中有 4% 的次品,而合格品中一等品 占 45% .从这批产品中任取一件,求该产品是一等品的 概率. 解:设A表示取到的产品是一等品,B表示取出 的产品是合格品, 则
P68 A 组第 2 题
选做作业: 根据以往的临床记录 ,某 种 诊 断 癌 症 的 试 1.
验具有如下的效果 :若以A 表示事件 "试 验 反 应 为阳性 " ,以 C 表 示 事 件 "被 诊 断 者 患 有 癌 症 ",则 有 P ( A C ) 0.95, P ( A C ) 0.95.现 在 对 自 然 人 群 进行普查 ,设 被 试 验 的 人 患 有 癌的 症概 率 为 0.005, 即 P (C ) 0.005, 试 求 P (C A).