人教版中职数学-概率初步

10.1计数原理【教学目标】1．理解分类计数原理与分步计数原理，会利用两个原理解决实际问题.2．培养学生利用数学思想方法分析、解决实际问题的能力．3．通过教学，让学生感受生活中的数学思想，提高数学的应用意识.【教学重点】两个计数原理的理解与应用．【教学难点】分类计数原理与分步计数原理的区别．【教学方法】本节课主要采用问题教学法．教师创设问题情景，引导学生观察发现分类计数原理与分步计数原理．并通过例题讲解，使学生进一步深化对定理的理解．最后通过对比实例，明确两个定理的联系和区别.10.2概率初步【教学目标】1．正确理解古典概型的两个特点，掌握古典概率计算公式．2．通过教学，发展学生类比、归纳、猜想等推理能力．3．通过古典概率解决游戏问题，培养学生的数学应用能力以及科学的价值观与世界观．【教学重点】古典概型特点，古典概率的计算公式以及简单应用．【教学难点】试验的基本事件个数n和随机事件包含基本事件的个数m．【教学方法】通过三个简单的例题让学生初步理解古典概型的特征，并由此引出样本空间和基本事件等诸多概念，教师紧扣这三个例题讲解各个概念，并由学生总结古典概率的计算公式．然后通过后面的例题巩固古典概率的求法．【教学过程】10.3.1总体、样本和抽样方法（一）【教学目标】1．理解总体、样本和随机抽样的概念，掌握简单随机抽样的两种方法．2．通过实例，体验简单随机抽样的科学性及可靠性，培养学生分析问题、解决问题的能力．3．通过对现实生活和其他学科中统计问题的提出，体会数学知识在实际生活中的重要应用．【教学重点】正确理解简单随机抽样的概念，掌握抽签法及随机数表法的步骤．【教学难点】能灵活应用抽签法或随机数表法从总体中抽取样本．【教学方法】这节课主要采取启发引导和讲练结合的教学方法．引导学生根据现实生活的经历和体验及收集到的信息来理解理论知识，同时通过例题、练习和课后作业，启发学生从书本知识回到社会实践，学以致用．10.3.1 总体、样本和抽样方法（二）【教学目标】1．理解系统抽样的概念，掌握系统抽样的一般步骤．2．通过实例的分析、解决，培养学生分析问题、解决问题的能力．3．通过数学活动，感受数学在实际生活中的应用，体会现实世界和数学知识的联系．【教学重点】掌握系统抽样的步骤．【教学难点】能够灵活应用系统抽样的方法解决统计问题．【教学方法】本节课采用启发引导和讲练结合的教学方法.教学中教师带领学生从系统抽样的定义分析得出系统抽样的方法和步骤，然后结合例题及其变式练习巩固系统抽样的步骤．10.3.1 总体、样本和抽样方法（三）【教学目标】1．正确理解分层抽样的概念，掌握分层抽样的一般步骤．2．区分简单随机抽样、系统抽样和分层抽样，能灵活选择适当的方法进行抽样．3．通过数学活动，感受数学在实际生活中的应用，体会现实世界和数学知识的联系．【教学重点】分层抽样的定义和步骤．【教学难点】利用分层抽样的方法解决现实问题．【教学方法】这节课主要采取启发引导和讲练结合的教学方法．教学中教师带领学生从分层抽样的定义分析得出分层抽样的方法和步骤，然后结合例题及课后练习巩固分层抽样的步骤．【教学过程】10.3.2频率分布直方图【教学目标】1．掌握列频率分布表、画频率分布直方图的步骤，会用样本频率分布直方图估计总体分布．2．培养学生利用数学方法分析数据、解决实际问题的能力．3．通过画频率分布直方图的过程，培养学生耐心细致，严谨认真的科学态度.【教学重点】绘制频率直方图.【教学难点】列出频率分布表．【教学方法】本节主要采用例题教学法．通过一个具体的题目，讲解极差、频率等概念，教师带领学生一步步列出例题的频率分布表，画出频率分布直方图．随着教师的讲解，学生分步练习，真正掌握画频率分布直方图的各个步骤.【教学过程】10.3.3 用样本估计总体【教学目标】1．理解样本平均数和总体平均数，会用样本平均数估计总体平均数．2．理解样本标准差的意义和作用，学会计算样本标准差，并能用样本标准差估计总体标准差．3．通过实例，让学生体会从特殊到一般的数学思想方法，通过感性认识帮助学生理解统计在社会生活中的重要作用．【教学重点】理解样本平均数，样本标准差的意义和作用，学会计算样本平均数和样本标准差．【教学难点】理解样本平均数及样本标准差的意义和作用．【教学方法】采用支架式教学方法．教师提供研究的材料和问题，即向上攀登的支架，从学生的认知规律出发，通过大量实例，引导学生自主探索解决问题的方法，通过合作讨论互相学习，取长补短，并归纳总结成一般规律，使得原有的认知结构得到进一步补充和完善．10.3.4 一元线性回归【教学目标】1. 了解相关关系、回归分析、散点图、回归直线方程的概念．2. 掌握散点图的画法，掌握回归直线方程的求解方法，会求回归直线方程．3. 让学生参与回归直线的探求，结合身边的实例，发现散点图的线性特征，主动构建线性回归直线方程的模型．【教学重点】散点图的画法，回归直线方程的求解方法．【教学难点】回归直线方程的求解方法．【教学方法】这节课主要采取启发引导和讲练结合的教学方法．通过创设情境、设置问题等手段对学生进行了启发、诱导，结合讨论法、讲授法组织学生自主探究．然后结合例题及课后练习巩固求回归直线方程的步骤．【教学过程】。

人教版中职数学(基础模块)下册10.2《概率初步》一、概率的基本概念概率是数学中一门与事件发生的可能性有关的学科，概率论的研究对象是随机现象及其规律性。

其中，事件是指试验中可能发生的某种结果，试验是具有随机性质的科学实验或实际现象。

概率是研究随机现象发生情况的一种科学方法。

概率有几种常见的表示方法：1、极限频率表示法：将事件A发生的次数除以试验总次数，当试验次数足够多时，就会趋近于一个固定值，称为事件A的极限频率，即为概率。

2、古典概型：将所有可能的基本事件的概率加起来，即可得到事件A的概率。

3、几何概型：将求概率问题转换为求几何面积或长度等问题，然后计算出几何面积或长度之比，即为概率。

二、概率的性质概率有以下几个性质：1、非负性：对于任意事件A，P(A) >= 0。

2、规范性：对于样本空间S中任意事件A，有P(S) = 1。

3、可列可加性：对于样本空间S中任意两个互不相容的事件A和B，有P(A或B) = P(A) + P(B) 。

三、概率计算概率计算主要分为以下三类：1、基本概率计算：根据随机现象的特征确定基本事件及其概率，并求出所需事件的概率。

2、条件概率计算：在已知某一事件发生的条件下，求另一事件发生的概率，表示为P(B|A)。

3、全概率计算：当样本空间S中有多个事件时，利用各个事件发生的概率及其对应的条件概率，求出任一事件的概率。

四、概率的应用概率在各个领域都有着广泛的应用。

以下是其中的几个例子：1、风险管理：概率被广泛应用于金融和风险管理领域，可用于评估不同资产的风险，决定投资组合和风险控制方案。

2、医学：概率可被用来评估疾病的风险和患病率，以及各种诊断测试的可靠性和准确性。

3、科学研究：概率被广泛应用于各种科学实验中，如物理学、化学、生物学等，可用于研究受试者的特征以及实验结果的可信度和可靠性等。

4、决策和规划：概率可应用于各个方面，如企业管理、市场预测、人力资源管理等领域，用于决策和规划。

人教版中职数学基础模块下册《概率初步》教学设计 (一)人教版中职数学基础模块下册《概率初步》是一本中职学生理解概率和统计学的重要教材。

在教学时，老师应该注重帮助学生理解概率和统计学的真正含义，以及如何应用这些概念到实际生活中。

下面是一份关于人教版中职数学基础模块下册《概率初步》教学设计的详细方案。

一、教学目标1. 让学生了解概率与统计学的基本概念和定义，包括概率、事件、随机试验、样本空间等；2. 让学生掌握常见的概率计算方法，包括加法原理、乘法原理、逆概率、条件概率等；3. 帮助学生理解概率的应用，如概率分布、期望、方差、标准差等；4. 促进学生分析和解决实际生活中的问题，如数字游戏、信用卡应用等。

二、教学内容1. 概率基本概念（1）概率的定义（2）事件与样本空间（3）随机试验2. 概率计算方法（1）加法原理（2）乘法原理（3）逆概率（4）条件概率3. 概率的应用（1）概率分布（2）期望（3）方差和标准差（4）数字游戏（5）信用卡应用三、教学方法1. 讲解教师可以借助ppt、黑板等多媒体来讲解概率的基本概念、方法和应用，使学生更加易于理解和记忆。

2. 实验在教学中，可以给学生准备一些随机试验的实验器材，如抛硬币、掷骰子等，让学生自己进行观察、实验和记录，从而更加深入地了解随机试验和概率的计算方法。

3. 活动在教学中，可以设置类似数字游戏的活动，让学生通过实践来探索概率的规律和计算方法，并从中感受到概率的应用。

四、教学步骤1. 导入通过简单的例子引入概率和统计学的概念，让学生了解概率和统计学是如何与我们的日常生活相联系的。

2. 讲解教师讲解概率的基本概念和计算方法，详细阐述各种情况下的计算方法。

3. 实验通过实验器材让学生进行随机试验和概率的计算，理解概率的含义和计算方法，提高学生的实践能力。

4. 活动设置数字游戏的活动，让学生通过实践来探索概率的规律和计算方法，并从中感受到概率的应用。

5. 练习通过大量的例题和习题让学生进行练习，让学生对所学到的概念和方法得到深刻的理解和掌握。

10.2 概率初步
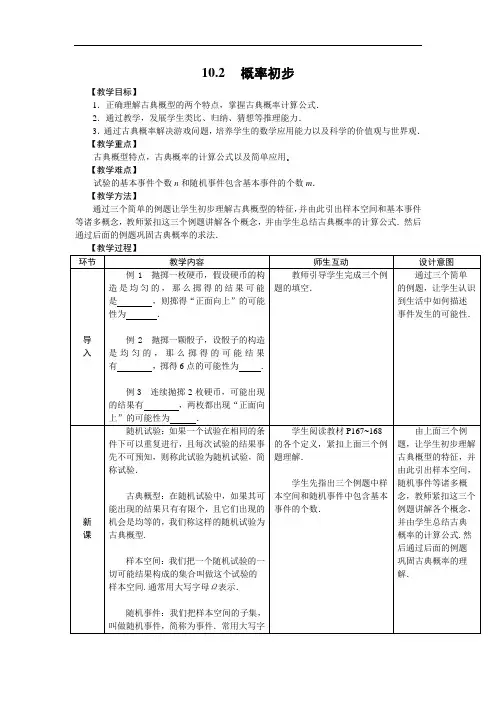
【教学目标】
1．正确理解古典概型的两个特点，掌握古典概率计算公式．
2．通过教学，发展学生类比、归纳、猜想等推理能力．
3．通过古典概率解决游戏问题，培养学生的数学应用能力以及科学的价值观与世界观．【教学重点】
古典概型特点，古典概率的计算公式以及简单应用．
【教学难点】
试验的基本事件个数n和随机事件包含基本事件的个数m．
【教学方法】
通过三个简单的例题让学生初步理解古典概型的特征，并由此引出样本空间和基本事件等诸多概念，教师紧扣这三个例题讲解各个概念，并由学生总结古典概率的计算公式．然后通过后面的例题巩固古典概率的求法．。

10.2 概率初步
【教学目标】
1．正确理解古典概型的两个特点，掌握古典概率计算公式．
2．通过教学，发展学生类比、归纳、猜想等推理能力．
3．通过古典概率解决游戏问题，培养学生的数学应用能力以及科学的价值观与世界观．【教学重点】
古典概型特点，古典概率的计算公式以及简单应用．
【教学难点】
试验的基本事件个数n和随机事件包含基本事件的个数m．
【教学方法】
通过三个简单的例题让学生初步理解古典概型的特征，并由此引出样本空间和基本事件等诸多概念，教师紧扣这三个例题讲解各个概念，并由学生总结古典概率的计算公式．然后通过后面的例题巩固古典概率的求法．。