单电子辐射跃迁选择定则的讨论
- 格式:doc
- 大小:633.08 KB
- 文档页数:16

第四章:碱金属原子和电子自旋锂、钠、钾、铷、铯、钫化学性质相仿、都是一价、电离电势都比较小,容易被电离,具有金属的一般性质。
一、碱金属原子的光谱1、四个线系(锂为例):其他碱金属光谱系相仿,只是波长不同主线系:波长范围最广,第一条线是红色的,其余在紫外,系限2299.7埃;第一辅线系(漫线系):在可见部分;第二辅线系(锐线系):第一条线在红外,其余在可见部分;伯格漫线系(基线系):全在红外。
2、巴尔末氢原子光谱规律: ,5,4,3),1-21(1~22===n nR v H λ 碱金属原子光谱:2*∞-~~nR v v n = R 为里德伯常数,当,所以∞v ~是线系限的波数,且有效量子数*n 不是整数,Δ==-*n TR n 3、碱金属原子的光谱项:22*Δ)-(n R n R T == 4、同一线系的有效量子数与主量子数差别不大;与某一量子数对应不同线系的有效量子数差别明显,引进角量子数加以区分:5、每一线系线系限波数恰好是另一线系第二谱项值中最大的那个。
共振线:主线系第一条。
6、碱金属原子氢原子能级的比较n 很大时,碱金属原子能级 很接近氢原子能级;n 较小时,碱金属原子能级 与氢原子能级相差大; 且n 相同,l 不同的能级高低差别很大。
二、原子实极化和轨道贯穿:原子=原子实+价电子1、原子实:碱金属原子中的电子具有规则组合,共同点是在一个完整的结构之外,多余一个电子,这个完整而稳固的结构称为原子实。
由于原子实的存在,发生原子实的极化和轨道在原子实中的贯穿。
2、价电子:原子实外的那个电子称作价电子。
价电子在较大的轨道上运动,与原子实结合不是很强,容易脱离。
它决定元素的化学性质,在较大的轨道上运动。
3、原子实的极化:由于价电子的电场的作用,原子实中带正电的原子核和带负电的电子的中心发生微小相对位移,于是负电的中心不再在原子核上,形成一个电偶极子。
① 角量子数l 小:轨道偏心率大(椭圆),极化强,能量影响大;② 角量子数l 大:轨道偏心率小(接近圆),极化弱,能量影响小。
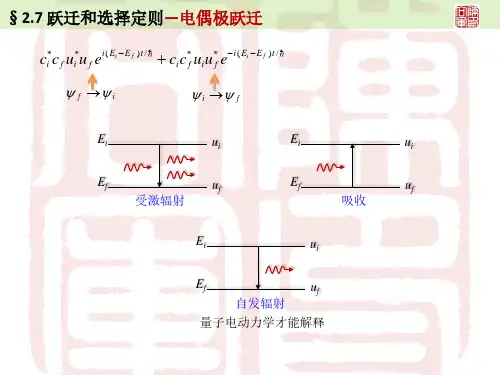







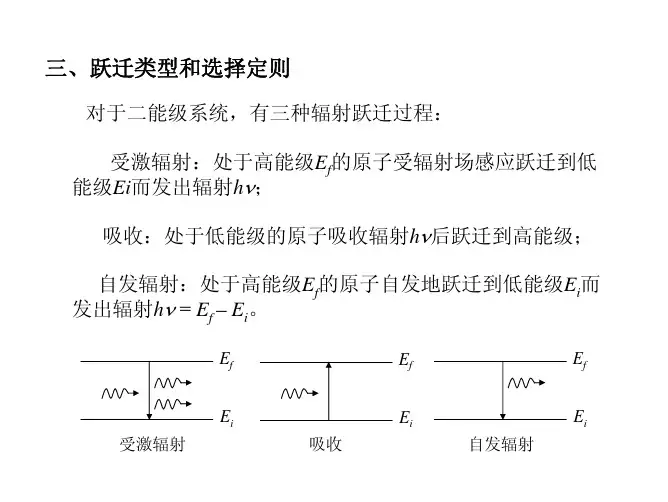

量子跃迁中的选择定则张扬威(华中师范大学物理学院2008级基地班,武汉,430079)摘 要 本文根据量子跃迁过程中遵从的角动量守恒和宇称守恒运用量子化概念,推导出电偶极近似条件下,在不同的外场中单电子原子以及多电子原子 辐射跃迁时的选择定则,并结合具体实例,说明这些规律的实质。
关键词 辐射跃迁 选择定则 角动量守恒 宇称守恒 原子态 电偶极近似 1 、 引言推微观粒子在不同的量子化状态间变化,称为跃迁。
跃迁有很多种,不同跃迁遵从不同的跃迁选择定则。
原子辐射跃迁的选择定则是原子能级之间发生跃迁所满足的条件,它对于研究光的吸收和发射具有很重要的意义。
由于电偶极矩跃迁强度比其它形式的跃迁强度大很多(倍),原子的辐射跃迁选择定则是指电偶极辐射跃迁选择定则。
它是从大量光谱的观察分析和研究中总结出来的,本文则运用量子力学的理论对它进行推导研究。
510~1082、 入射光为单色偏振光引入周期性微扰下的跃迁概率的基本知识:设微扰Hamilton 算符为(式中为与无关的厄米算符)'0(0)A cos ()(0)i t i t H t t F e e t ωωω∧∧∧−=<=+≥或 (1)体系在处于'0t =(0)n ϕ态, 跃迁到态的概率为't =t (0)m ϕ22(0)(0)2()()n m m mn m n W a t F E E πδω→==−±h h(2) 若该单色偏振光是沿x 轴 方向传播,偏振方向沿z 轴,在电偶极近似条件下,它的电场为0cos z t εεω= 0x ε= 0y ε= (3)电子的电偶极矩为 D er ex =−=−r(4)微扰作用势为 '00cos ()2i t i tz ez H D ez ez t e e ωωεεεεω∧−=−===+r uv (5) 对比(1)式可得 02ez F ε∧=(6) 带入(2)式可得 222(0)(0)0()2n m mn m n e W z E E πεδω→=−h h±(7)由(7)式可以得出,原子能否由n 态跃迁到m 态,决定于电子位矢的z 分量在这两个态之间的矩阵元mn z 是否为零。
2.5.5 跃迁选律内容更新如下:原子光谱是原子能级之间的跃迁产生的。
但在原子世界中, 这种跃迁也必须遵从某些规则, 并不是任何两个能级之间都可以随便跃迁。
这些规则就是所谓的“跃迁选律”。
允许的电偶极跃迁选律如下:ΔS = 0ΔL = 0,±1(但从L=0到L=0禁阻。
单电子原子基态为s态,L=0,对于它们来说,如果跃迁是ΔL = 0, 就只能从L=0到L=0, 而这是禁阻的。
因此,只有ΔL=±1)ΔJ = 0,±1(但从J=0到J=0禁阻)ΔMJ = 0,±1(但ΔJ = 0时, 从MJ= 0到MJ= 0禁阻)这些选律在轨道-自旋耦合作用变强时会逐渐失效, 而在j-j耦合方案中会变得完全不起作用。
因为在这种情况下,就连量子数L和S本身都已经越来越没有确定值,用量子力学的语言说,它们不再是好量子数。
所以, ΔS≠0的跃迁在轻原子中非常弱, 而在重原子中可能相当强,因为轨道-自旋耦合随原子序数的4次方增长。
此外, 原子都是中心对称的, 所以, 跃迁还要受到Laporte选律的限制。
为了搞清什么是Laporte选律, 首先需要知道谱项的宇称。
我们还记得, 原子轨道都有确定的宇称。
电子排布在轨道上形成组态, 进而确定了谱项, 所以, 谱项也有确定的宇称。
用下列两种方法的任意一种,很容易求出谱项的宇称:(1) 对于组态中各个电子的轨道角量子数l 求和,总和的奇偶性就等于该组态产生的所有谱项的奇偶性。
即: 总和若为偶数, 谱项的宇称为g; 总和若为奇数, 谱项的宇称为u 。
(2) 将组态中各个电子按所在轨道的宇称相乘(同样是,每个电子一项, 而不是每个轨道一项),这种乘积叫做“直积”,所以使用特殊的乘号⊗。
乘法规则是:g ⊗g=u ⊗u=g , g ⊗u=u ⊗g=u 。
谱项的宇称为u 时,以O 作为右上标。
电偶极跃迁的Laporte 选律: 电偶极跃迁只能发生在宇称不同的态之间。
单电子辐射跃迁选择定则的讨论(理学院物理系物理学)摘要原子辐射跃迁选择定则是原子物理学中的一个重要原则。
本文主要采用两种方法对单电子辐射跃迁选择定则进行讨论。
第一种方法,利用量子方法讨论;第二种方法,利用半经典方法讨论;两种方法分别对电子的轨道和自旋有无耦合的情况下进行了推导。
用两种不同的方法,得到了一致的结果。
关键词:电偶极辐射;跃迁几率;角动量守恒;量子数;选择定则Discussion of Single Elect ron’s transition Selection Rule(Department of Physics, College of science, Physics )AbstractSelection rule of atom transition is one of the important principles in the atom physics. This paper adopts two methods to discuss the selection rule of the single electron transition.In the first method, quantum method is used to analyze the problem.In the second method, semiclassical method is used to discuss the thesis. Two cases that the electric orbit and spin have coupling and no coupling are respectively discussed in both methods. By two different methods, the same result is conclued.Keywords:Electric dipole radiation;Transition probability;Conservation of angular momentum;Quantum number;Selection rule目录1 引言 (1)2 量子方法讨论选择定则 (1)2.1 电子的轨道和自旋无耦合的情况 (1)2.2 电子的轨道和自旋有耦合的情况 (3)3 半经典方法讨论选择定则 (7)3.1 角动量的矢量合成法则 (7)3.2 电子组态变动定则 (7)3.3 L S-无耦合的跃迁选择定则 (9)3.4 L S-有耦合的跃迁选择定则 (10)4 结论 (11)参考文献 (12)致谢 (13)1引言微观粒子(分子、原子、原子核、基本粒子等)的运动规律,是本世纪二十年代在总结大量实验事实和旧量子论的基础上建立起来的。
跃迁选择定则
跃迁选择定则是指在原子或分子中,电子从一个能级跃迁到另一个能
级时,必须满足一定的选择定则。
这些选择定则是由量子力学的原理所决
定的,它们描述了跃迁的可能性和概率。
其中最基本的选择定则是电偶极
辐射选择定则,它规定了只有在电偶极矩发生变化的跃迁才会发生辐射。
这意味着只有在两个能级之间的电偶极矩不为零时,才会发生跃迁。
另一
个重要的选择定则是自旋选择定则,它规定了只有在自旋量子数不变的情
况下,才会发生跃迁。
这意味着只有在两个能级之间的自旋量子数相同时,才会发生跃迁。
除了这些基本的选择定则外,还有一些其他的选择定则,
如角动量选择定则、偶极矩选择定则等。
这些选择定则在量子力学中起着
非常重要的作用,它们帮助我们理解原子和分子的光谱学行为,以及它们
在化学反应中的作用。
单电子辐射跃迁选择定则的讨论(理学院物理系物理学)摘要原子辐射跃迁选择定则是原子物理学中的一个重要原则。
本文主要采用两种方法对单电子辐射跃迁选择定则进行讨论。
第一种方法,利用量子方法讨论;第二种方法,利用半经典方法讨论;两种方法分别对电子的轨道和自旋有无耦合的情况下进行了推导。
用两种不同的方法,得到了一致的结果。
关键词:电偶极辐射;跃迁几率;角动量守恒;量子数;选择定则Discussion of Single Elect ron’s transition Selection Rule(Department of Physics, College of science, Physics )AbstractSelection rule of atom transition is one of the important principles in the atom physics. This paper adopts two methods to discuss the selection rule of the single electron transition.In the first method, quantum method is used to analyze the problem.In the second method, semiclassical method is used to discuss the thesis. Two cases that the electric orbit and spin have coupling and no coupling are respectively discussed in both methods. By two different methods, the same result is conclued.Keywords:Electric dipole radiation;Transition probability;Conservation of angular momentum;Quantum number;Selection rule目录1 引言 (1)2 量子方法讨论选择定则 (1)2.1 电子的轨道和自旋无耦合的情况 (1)2.2 电子的轨道和自旋有耦合的情况 (3)3 半经典方法讨论选择定则 (7)3.1 角动量的矢量合成法则 (7)3.2 电子组态变动定则 (7)3.3 L S-无耦合的跃迁选择定则 (9)3.4 L S-有耦合的跃迁选择定则 (10)4 结论 (11)参考文献 (12)致谢 (13)1引言微观粒子(分子、原子、原子核、基本粒子等)的运动规律,是本世纪二十年代在总结大量实验事实和旧量子论的基础上建立起来的。
随着它的出现,人类对于物质微观结构的认识日益深入,从而能较深刻地掌握物质的微观理论,为用于生产开辟了广阔的途径。
电子跃迁就是微观状态发生跳跃式变化的过程。
由于微观粒子的状态常常是分立的,所以从一个状态到另一个状态的变化常常是跳跃式的。
跃迁选择定则有很多种,不同跃迁遵从不同的跃迁选择定则。
从跃迁的性质来分,主要分为电性和磁性两种。
在原子物理中涉及的L-S 耦合跃迁选择定则指的是电偶极矩跃迁,原因是电偶极矩跃迁强度比磁极跃迁和多极矩跃迁强度大得多(5810~10倍)。
原子的辐射跃迁选择定则也是指电偶极辐射跃迁选择定则。
本文采用量子和半经典两种方法,分别从电子的轨道和自旋(L-S )有无耦合的情况下对电偶极辐射跃迁选择定则加以讨论。
使人们对单电子辐射跃迁选择定则有更加深入的理解。
2量子方法讨论选择定则下面分别从电子的轨道和自旋有无耦合的情况下对单电子辐射跃迁选择定则进行讨论。
2.1电子的轨道和自旋无耦合的情况原子对光的发射和吸收是原子体系与光相互作用所产生的现象。
当光照射到原子上时,光波中的电场ε和磁场B 都对原子中的电子有作用,但和电场的作用相比较,磁场对电子的作用可以忽略,所以只考虑光波中的电场对电子的作用。
对于入射光为各向同性,且偏振是无规则的,则原子体系在单位时间内由k Φ态跃迁到m Φ态的几率为:()222243s k mmk mk e w I r πω→= (1)由此可知,当且仅当mk m k r r φφ= 不为零,即其三个直角坐标系分量,mk mk z x 和mk y 不全为零时,原子光吸收的跃迁几率方不为零。
再由:22243s km mkmk e B B r π== (2)222mkkm km A B cωπ= (3)两式可知原子受激发射和自发发射的跃迁几率也不为零。
其中 km B 表示吸收系数,mk B 表示受激发射系数,km A 表示自发发射系数。
这称原子在0m E 和0k E 两能级之间的跃迁是允许的。
否则,辐射跃迁是禁戒的。
因此0mk r ≠这个条件,可以得出产生原子跃迁选择定则。
我们具体讨论氢原子、类氢离子及碱金属原子。
其哈密顿算符写成为()2ˆˆ2p H V r μ=+ 其本征矢量若用电子自旋——轨道角动量无耦合的态矢量,,,l s n l m m ,在ˆr和ˆz s 共 同表象写为:()()()(),,l slsnlm mz nl lm m z r s R r Y X s ψθϕ= (4)则mk z 的具体形式是:ˆ,,,,,,l s l s n l m m z n l m m ''''()()*cos s s n l m l lm m nlm r r r d δψθψτ''''=⎰()()()()2*3*0,cos ,s s n l l l m m nl l m lm R r R r r dr Y Y d ππδθϕθθϕ''∞'''=Ω⎰⎰⎰(5)利用球谐函数的一个递推公式:1,1,cos l ll lm l ml m Y θ+-=+ (6)及球谐函数的正交归一化表示式,可知若满足:100l l l s s s l l l m m m m m m '''∆=-=±∆=-=∆=-= (7)时,则矩阵元ˆ,,,,,,0l s l s n l m m z n l m m ''''≠ 同样,mk x 和mk y 的具体形式分别为:ˆ,,,,,,l s l s n l m m x n l m m '''' ()()*sin cos s s n l m l lm m nlm r r r d δψθϕψτ''''=⎰()()()()2*3*0,sin ,2s s n l l l i i m m nl l m lm e e R r R r r dr YY d ϕϕππδθϕθθϕ''-∞'''+=Ω⎰⎰⎰(8) ˆ,,,,,,l s l s n l m m y n l m m '''' ()()*sin sin s s n l m l lm m nlm r r r d δψθϕψτ''''=⎰()()()()2*3*,sin ,2s s n l l l i i m m nl l m lm e e R r R r r dr YY d ϕϕππδθϕθθϕ''-∞'''-=Ω⎰⎰⎰(9) 利用球谐函数的另一个递推公式:1,11,1()(1)sin (2(21)(21)l l l i l l l lm l m l m l m l m l m e Y Y l l l ϕθ±+±-±±+-=±+-+ (10)及球谐函数的正交归一化表示式可知,若110l l l s s s l l l m m m m m m '''∆=-=±∆=-=±∆=-= (11)时,则矩阵元ˆ,,,,,,0l s l s n l m m x n l m m ''''≠ ˆ,,,,,,0l s l s n l m m y n l m m ''''≠ 综合(7)(11)两式可知:100l s l m m ∆=±∆=∆=为跃迁的电偶极辐射选择定则。
原子的两个定态,,,l s n l m m ''''和,,,l s n l m m 之间如果满足上式,则在电偶极近似下光吸收和发射的跃迁几率不等于零,会有光谱线产生。
2.2电子的轨道和自旋有耦合的情况原子由一种态跃迁到另一种态有一定的几率,设电子的自旋和轨道有耦合作用下电子的本征态为j nljm ψ。
则电子由态j nljm ψ跃迁到jn l j m ψ''''电偶极自发跃迁几率为:222343n n n n e A r cω''→= (12) 其中,n n '各代表4个量子数,()nl n l E E ω''=-。
上式中2222n n n n n n n n r x y z ''''=++ (13)三个矩阵元中至少有一个不等于零,跃迁才是允许的。
j nljm ψ可以表示为:()(),,jj nljmnl ljm z R r s ψφθϕ= (14)其中()nl R r 为径向波函数,j ljm φ为()22,,z l j j 的共同本征函数,可以分成两类:,111,,22jlm A jm j l m j l m m φ+⎫⎪==+=+⎪⎭(15),111,,22jl m Bjm j l m j l m m φ''+⎛⎫'⎪==-=+⎪⎭(16) 利用式(14),矩阵元n n r '可以分离变量地表示成:3jj n n l j m ljm n l nl rr R R r dr rφφ∞''''''︒=⎰(17)其中径向积分通常与选择定则无关。
利用公式2rr rr γγγσσσσσσ⎛⎫=+=⋅ ⎪⎝⎭ (18)jjjjA B B Ajm jmjm jmγγσφφσφφ=-=-(19)即得jj j j j j B B A A A A j m jm j m jm j m jm r r r r r rγγφφφσσφφφ''''''==,()21γσ= (20) 类似地,可得jj j j B A A Bj m jm j m jm r r r rφφφφ''''=(21)再利用(18)式,可得2jj j j j j A A A B B Aj m jm j m jm j m jm r rφφφσφφσφ''''''-=+(22)'2j j j j j jB A A A B B jm j m jm j m jm j m r rφφφσφφσφ'''''-=+ (23) 利用Pauli 矩阵σ的具体形式为:0110x σ⎛⎫= ⎪⎝⎭ ,00y i iσ-⎛⎫= ⎪-⎝⎭ ,1001z σ⎛⎫= ⎪-⎝⎭以及lm Y 的正交归一性和式(15)(16)(17)三式就可算出这些矩阵元。