当前位置：文档之家 › 多电子原子光谱-- 电偶极跃迁的选择定则

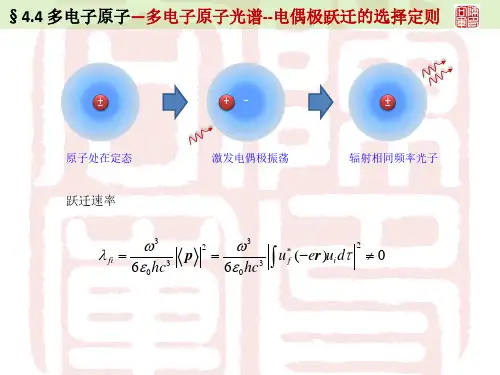
多电子原子光谱-- 电偶极跃迁的选择定则

  • 格式：pdf
  • 大小：866.25 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

跃迁类型和选择定则

跃迁类型和选择定则

同样，氦的21S0到基态11S0也不能进行电和磁的单光子跃迁， 它们之间主要的是双光子跃迁过程。 在激光的强相干场中，双光子过程才变得重要。 现在经常利用功率较大的可调频率激光器来研究双光子和多 光子跃迁等极小概率过程。
2(1)
591.4
3888.6 7065.2 169082.185 169081.189 169081.111 10830
2(2,1,0)
2(1)
159850.318
1(0)
(cm–1)
图 2.1.1 HeI 的衰变图和能级图
磁偶极辐射和电四极辐射的选择定则
定则 1 2 3 4 电偶极跃迁E1
ΔJ = 0, ±1,
辐射跃迁矩阵元：
ˆ M ba = ψ b e−ik ⋅r ε ⋅∇ ψ a
kr的数量级为10-3，是一个小量。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
如果忽略一次以上项，即取 则有
E1 ba
e
− ik ⋅r
≈1
( Dba = −erba )
M
mωba ˆ = ε ⋅ Dba e
2
电偶极矩-er在空间反演下变号，宇称为奇，P = -1。由于 宇称守恒，初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献，要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的，P = 1， 由于宇称守恒，初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称，以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系：

laporte定则

laporte定则

Laporte定则
Laporte定则是一种描述分子中电子的能级跃迁的规则。

它指出，在一个多电子原子或分子中，当电子从一个能量较低的轨道跃迁到另一个能量较高的轨道时，会释放出一定数量的能量。

这个能量可以通过发射光子的方式释放出来，也可以通过吸收光子的方式吸收能量。

Laporte定则的基本思想是，在一个多电子原子或分子中，电子的能量是由其轨道的量子数和角动量量子数决定的。

根据Laporte定则，当一个电子从一个能量较低的轨道跃迁到另一个能量较高的轨道时，必须满足以下三个条件：
1. 电子跃迁前后的总角动量量子数必须相等。

2. 电子跃迁前后的总自旋角动量量子数必须相等。

3. 电子跃迁前后的总轨道角动量量子数必须相等。

如果这三个条件都得到满足，那么电子跃迁就可以发生，并且会释放出能量。

Laporte定则是描述分子光谱的重要工具之一，可以用来解释分子光谱中的各种现象，如吸收光谱和发射光谱等。

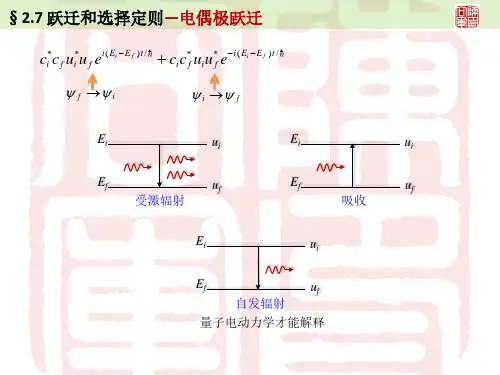
7跃迁和选择定则电偶极跃迁

7跃迁和选择定则电偶极跃迁

F
=
−∇U
=
−
i
∂U ∂x
+
j ∂U ∂y
+ k ∂U ∂z
其直角坐标分量
Fx
= − ∂U ∂x
= µx ∂∂Bxx
+ µy
∂By ∂x
+ µz
∂Bz ∂x
Fy
= − ∂U ∂y
= µx ∂∂Byx
+ µy
∂By ∂y
+ µz
∂Bz ∂y
Fz
= − ∂U ∂z
= µx ∂∂Bzx
+ µy
f
= exp −
ω kBT
exp
−
ω kBT
= Bif I (ω) Afi + Bfi I (ω)
I (ω) = Afi
1
Bif
ω
exp
kBT
−
B fi Bif
§2.7 跃迁和选择定则—Einstein辐射唯象理论
Planck黑体辐射公式
I (ω)
=
ω3 π 2c3
exp
∂By ∂z
+ µz
∂Bz ∂z
如果磁场是均匀的，梯度为零，则磁矩所受力为零。
§3.1 轨道磁矩和Stern-Gerlach实验—磁矩与磁场相互作用
磁矩受到的力矩： τ= µ × B
B
力矩的作用将引起角动量的变化
τ= dL= µ × B
dt
在均匀磁场中磁矩虽然不受净平移力的作用，但仍要受 到一个力矩作用
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s，相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态，τ＝∞，相应的 Γ = 0。

多电子原子光谱--电偶极跃迁的选择定则-USTC

多电子原子光谱--电偶极跃迁的选择定则-USTC

P. V. Auger (1899-1993)
K壳层出现一个空位后，一个L壳层s支壳层上的电 子(2s电子)跃迁到K壳层填充这个空位，释放出的 能量传递给L壳层p支壳层上的一个电子(2p电子)并 使之电离，这一过程称为KLILII,III俄歇跃迁。
俄歇电子的动能
EA = EK − ELI − ELII ,III
轫致辐射(bremsstrahlung，刹车辐射)
hν= T − T ′
hν max=
hc =
λmin
T=
eU
杜安(W. Duane)和亨特(P. Hunt)于1915年实验测定了h 值，与利用光电效应 实验测定的h值十分接近。
§4.5原子的内层能级和特征X射线—X射线的能谱 X射线特征谱
当加速电压大于一定值时，在连续谱 上出现了分立的线谱：
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
+-
+-
+-
原子处在定态
激发电偶极振荡
辐射相同频率光子
跃迁速率
∫ λ=fi
ω3 6ε 0 hc3
2
p=
ห้องสมุดไป่ตู้
ω3 6ε 0 hc3
2
u
* f
(−er
)ui
dτ
≠0
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
电偶极辐射的选择定则 (多电子原子情形) 拉波特定则：跃迁只允许在宇称相反的态之间发生。
W. L. Bragg (1890-1971)
布拉格条件(相干加强) 2= d sinθ n= λ, n 1, 2,3
大布拉格的X射线分光仪
W. H. Bragg (1862 -1942)

跃迁类型和选择定则

跃迁类型和选择定则

将原子和电偶极辐射场作为一个整体系统处理，用k表示 辐射的波矢，ε表示偏振态，-er是电偶极矩。 如果系统处在有nk,ε个量子的初始态（用i标记）中，则单 位时间内系统跃迁到有nk,ε+1个量子的终态（用f标记）的跃迁 速率为
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
M ˆ M ba1E2 = ψ b (ik ⋅ r )(ε ⋅∇) ψ a M E = M ba1 + M ba2
其中
M
M1 ba
=−
ωba
2 c
ψ b ly ψ a
E M ba2
2 imωba =− ψ b xi zi ψ a 2 c
原子序数为Z的类氢离子的磁偶极跃迁的跃迁速率与电 偶极跃迁速率之比为：
三、跃迁类型和选择定则
对于二能级系统，有三种辐射跃迁过程： 受激辐射：处于高能级Ef的原子受辐射场感应跃迁到低 能级Ei而发出辐射hν； 吸收：处于低能级的原子吸收辐射hν后跃迁到高能级； 自发辐射：处于高能级Ef的原子自发地跃迁到低能级Ei而 发出辐射hν = Ef – Ei。
Ef Ei 受激辐射 吸收 Ef Ei 自发辐射 Ef Ei
2
电偶极矩-er在空间反演下变号，宇称为奇，P = -1。由于 宇称守恒，初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献，要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的，P = 1， 由于宇称守恒，初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称，以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系：

多原子分子的电子光谱

多原子分子的电子光谱
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)0
3. 有两个单占据轨道(都是非简并轨道)的组态 谱项的对称性由这两个单占据轨道的直积给出, S = 0 或 1, 多重度为 1 或 3。 如乙烯的激发态 (D2h) 有以下组态: ···(b3u)1(b2g)1 b3ub2g = B1u，其谱项为：1B1u，3B1u。
当Qi为非全对称的一维不可约表示，则：
Vi Vi' Vi'' 0, 2, 4,
当Qi为二重简并态，并受到多重激发，则： li 0
Vi Vi' Vi'' 0, 2, 4,
若电子和振动的相互作用很大，则由下式确定：
R e'V 'e''V '' 'eV 'e' V
电子振动态的选择定则比纯电子态的选择定则
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)0
2. 只有一个单占据轨道的电子组态 谱项由该轨道的对称性决定， 多重度为 2S + 1 = 2。 例如若组态为：
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)1 则其谱项为：2B1。
CO2电子组态: (1g)2(1u)2(2g)2(3g)2(2u)2(4g)2(3u)2 (1u)4(1g)4。 H2O (C2V) 的电子组态:
若 e 是简并态，则对操作 R 有：
Rˆl Djl (R) j
j
简并态的波函数构成一个多 维不可约表示的基函数。
§9.2 分子轨道与电子组态
一、电子组态
电子组态：将电子波函数看成单电子波函数的乘
积，考虑到自旋，每个轨道放两个电子，按分子

第五章多电子原子

第五章多电子原子

❖
17、儿童是中心，教育的措施便围绕 他们而 组织起 来。上 午11时15分58秒上午11时15分11:15:5821.7.23
❖ 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒，而是机会之杯。二〇二一年六月十七日2021年6月17日星期四
28
（5）洪特定则
每个原子态对应一定的能级。由多电子组态形成的原子态 对应的能级结构顺序有两条规律可循：
洪特定则： 从同一电子组态形成的诸能级中， （1）那重数最高的，亦即S值最大的能级位置最低； （2）从同一电子组态形成的，具有相同S值的能级中 那些具有最大L值的位置最低。
*对于同一L不同J的能级次序: 当最小J值（|L－S|）的能级
15
一、电子组态:
电子组态: 处于一定状态的若干个（价）电 子的组合（n1l1 n2l2 n3l3…) 。
例：氦原子基态: 1s1s
镁原子基态: 3s3s
第一激发态: 1s2s
第一激发态: 3s3p
两个电子之间的相互作用:
1# n1l1s1=1/2
l1
G3 l1, s1
s1
Gl1,l2
G5l1,s2
PS S(S 1)
其量子数S取值限定为
s1 s2; s1 s2 1 s1 s2
当ss11
s2取2s2 s2取2s1
1个值 1个值
PSz mS
mS取从 S到S共2S 1个值
21
当s1=s2=1/2时:
S=0, ms=0

电偶极跃迁的选择定则

电偶极跃迁的选择定则

电偶极跃迁的选择定则电偶极跃迁的选择定则，听起来像个科学家开的玩笑，其实它可真是个有趣的课题。

想象一下，原子就像个跳舞的舞者，而电偶极跃迁就是它在舞台上的表演。

这个舞者可以在不同的能量状态之间切换，但并不是随便怎么跳舞都行哦。

它有一套自己的规则，就像跳舞的时候不能乱扭，得跟着节拍走。

让我们聊聊什么是电偶极跃迁。

简单来说，这就是原子或分子吸收或发射光子的时候发生的一种能量变化。

想象一下，原子像个孩子，光子就像一颗糖果。

孩子看到糖果，就会兴奋地跳起来，直接把手伸向那颗糖。

这个过程其实是能量的转移，能量高的时候就是个兴奋的小家伙，能量低的时候就是乖乖待在原地的老实人。

说到这里，有趣的事情来了。

不是所有的糖果都能吸引每个孩子，这就是选择定则的魅力所在。

电偶极跃迁的选择定则告诉我们，只有特定的能量状态才能进行跃迁。

换句话说，有些能量状态就像是孩子的“心头好”，而有些则是“看不上”的。

就像你去吃自助餐，看到那道你最爱吃的菜，立马就扑过去了，别的菜根本没在你的考虑范围内。

再来谈谈这个选择定则的具体条件。

一般来说，跃迁的起始和结束状态之间的量子数差必须符合特定的条件。

比如，主量子数、角动量量子数等的变化都有讲究。

简单点说，有点像打麻将，不能随便碰牌，要符合规则才能成牌。

如果不符合这些条件，跃迁就像是碰上了阻碍，想跳也跳不起来。

咱们再来细聊聊偶极矩的概念。

这个偶极矩就像是舞者的舞姿，能量的高低、位置的变化都会影响它的表现。

强的偶极矩意味着跃迁更容易发生，就像一位舞者跳得越好，观众自然就越喜欢。

反之，偶极矩弱，那就很可能在舞台上显得有些尴尬。

哦，大家都知道，尴尬的舞者很容易就会被观众遗忘。

有趣的是，选择定则也让我们对光谱的理解更加深入。

不同的原子和分子有不同的跃迁方式，发出的光谱线就像他们的名片，清晰地显示出它们的特性。

比如说，氢原子和氦原子虽然都是气体，但它们的光谱完全不同。

就好比两个不同风格的明星，虽然都在演戏，但一开口就能让你认出来。

电偶极辐射跃迁选择定则与守恒定律

电偶极辐射跃迁选择定则与守恒定律

电偶极辐射跃迁选择定则与守恒定律
金蓉
【期刊名称】《山西师范大学学报（自然科学版）》
【年(卷),期】1999(013)003
【摘要】本文从角动量守恒定律和宇称守恒定律出发，运用量子化角动量的矢量
合成法则以及关于波函数的初步知识，给出了电偶极辐射跃迁选择定则的简单推导，力求在原子物理范围说明跃迁选择定则是跃迁中角动量守恒和宇称守恒的表面。

【总页数】4页(P49-52)
【作者】金蓉
【作者单位】四川成都师范专科学校
【正文语种】中文
【中图分类】O562.2
【相关文献】
1.稀土离子激活发光材料中能级跃迁的选择定则 [J], 尹民;闻军;段昌奎
2.单电子辐射跃迁选择定则的讨论 [J], 牛振风
3.轨道自旋耦合电偶极辐射跃迁选择定则探讨 [J], 李艳华
4.电偶极辐射跃迁中选择定则的理论研究 [J], 刘慧英;孙玉兰
5.MCDF程序包和电偶极辐射跃迁几率的相对论计算程序 [J], 朱颀人;潘守甫
因版权原因，仅展示原文概要，查看原文内容请购买。

多电子原子的光谱项

多电子原子的光谱项

这些实验技术能够精确地测量超精细结构能级分裂的大小和形
03
状，从而揭示原子核和电子之间的相互作用机制。
06
总结与展望
本文主要内容和创新点回顾
介绍了多电子原子的基本概念 和理论框架，包括原子结构、
电子组态、光谱项等。
详细阐述了多电子原子光谱项 的计算方法和实验技术，包括 变分法、微扰法、组态相互作
光谱支项确定及标记规则
光谱支项确定
根据泡利原理，同一电子组态可以形成的光谱项数目由电子数n和轨道数l决定。对于给定的电子组态，可以形成 的光谱项数目为(2l+1)。
标记规则
光谱项用大写英文字母S、P、D、F等表示，分别对应于L=0、1、2、3等。对于多重态，用数字2S+1表示，其 中S为总自旋量子数。例如，对于钠原子的3s^1电子组态，可以形成的光谱项为^2S_(1/2)。
电子自旋与轨道运动耦合
多电子原子中，电子自旋与轨道运动之间存在相互作用，导致能级发生分裂， 形成精细结构。
自旋-轨道耦合强度
自旋-轨道耦合强度与原子序数的平方成正比，因此重元素中精细结构现象更为 显著。
相对论效应对精细结构影响
质量速度关系
相对论效应导致电子质量随速度增加而增大，进而影响电子 在原子中的运动状态。
谱线强度与选择定则
谱线强度
表示原子光谱中某条谱线的发光 强度或吸收强度，与跃迁几率和
原子浓度等因素有关。
选择定则
决定原子能级间跃迁是否发生的规 则，如电偶极辐射的选择定则要求 Δl=±1。
影响因素
谱线强度受温度、压力、磁场等外 部条件的影响，同时也与原子本身 的性质有关。
02
多电子原子结构特点
电子云分布与形状

宇称—原子状态的奇偶性态

宇称—原子状态的奇偶性态

• j-j 耦合 J J P je
sP (sP 1) s(s 1)
J LS
对三个或三个以上价电子的原子，洪特定则，朗德间隔特定则仍
有效。对同科电子仍需考虑泡利原理。
同一次壳层由同科电子构成。同科 s 电子最多只能有2个，同科 p 电子最多6 个，同科 d 电子最多10个，…
➢ 多个电子同时激发到高能级 双里德伯态原子：现在应用激光技术，将两个电子同时激发到高
➢ 多价电子的原子态
任何原子的状态，都可以看作它的一次电离的离子加一个电子形成 的。而它的一次电离离子的状态同按周期表顺序前一个元素的状态 相似，所以有前一个元素的状态可推知后继元素的状态。
• L-S耦合
LP e
L LP Le S S p Se
n2 n3 n3 n4
三层能级之间的跃迁产生一组复杂结构的谱线
主线系：
~ 23S1 n3P0,1,2 , n 2
第二辅线系： 第一辅线系：
~ ~ ~
2233PP00,1,2n3Dn31S1 23P1 n3D1,2
, ,
n
3 n3
基线系：
~ ~ ~ ~
23P2
n3D1,2,3
33D1 n3F2 32D2 n3F2,3
❖ 电离电势和激 发电势较低
3P2
•存在两个亚稳态
3P1
3P0
6s6p的3P2和3P0
汞原子能级图
四. 复杂原子光谱的一般规律
➢ 位移定律
具有原子序数Z的中性原子的光谱和能级，同具有原子序数Z+1的 原子一次电离后的光谱和能级很相似 — 光谱和能级的位移定律。
➢ 多重性的交替律
元素周期表中相邻元素原子的能级多重数呈奇偶交替变化 — 原子 能级多重性的交替律。

宇称—原子状态的奇偶性态

宇称—原子状态的奇偶性态

➢ 多价电子的原子态
任何原子的状态，都可以看作它的一次电离的离子加一个电子形成 的。而它的一次电离离子的状态同按周期表顺序前一个元素的状态 相似，所以有前一个元素的状态可推知后继元素的状态。
• L-S耦合
LP lP (lP 1) Le l(l 1)
SP Se
L LP Le S S p Se
• j-j 耦合 J J P je
sP (sP 1) s(s 1)
J LS
对三个或三个以上价电子的原子，洪特定则，朗德间隔特定则仍
有效。对同科电子仍需考虑泡利原理。
同一次壳层由同科电子构成。同科 s 电子最多只能有2个，同科 p 电子最多6 个，同科 d 电子最多10个，…
➢ 多个电子同时激发到高能级 双里德伯态原子：现在应用激光技术，将两个电子同时激发到高
忽略
介质
热平衡 状态
粒子数 反转态
N2
E2 E1
e kT
1
N1
光强 I 的变化
N1 N2 I 0
N2 N1 I 0
说明
若介质处于粒子数反转态，光在其中传播时得以放大。 采用光泵浦方法。
例 He-Ne（5:1或10:1）激光器中Ne气粒子数反转态的实现
• 激活介质中光强随传播距离的变换关系 激活介质：处于粒子数反转态的介质。光传播时被放大。
末 系
的 2发
射
与
吸
收 1
• 热激发原子的能量分布
达到热平衡状态时( T ) ，各状态的原子数
E3
E2
N i e Ei / kT
若能级是 gi 重简并的
E1
Ni
g e Ei / kT i
N g e i
i ( Ei E1 ) / kT

利用d3群导出电子的电偶极跃迁的选择定则

利用d3群导出电子的电偶极跃迁的选择定则

利用d3群导出电子的电偶极跃迁的
选择定则
驱动器是电子工程中至关重要的一环，其中一类就是电偶极跃迁，根据电偶极
跃迁的不同功能，有着不同的选择定则。

首先，要根据系统的需求选择电极跃迁的应用类型。

如果需要大范围的快速跃
迁电偶，则可以选择三端式电极跃迁。

相比起单端式电极跃迁，它更为稳定而且更加有力，适用于大范围的快速跃迁。

其次，根据输出信号的要求，选择跃迁电偶的品种。

一般情况下，若需要得到
清晰的输出信号，则可以采用晶体管和功率放大器搭配使用。

如果需要稳定的运行，可以采用高压金属氧化物半导体反激控制电偶跃迁。

再次，要根据电偶跃迁应用领域的不同，选择适合的跃迁电偶。

对于电子时钟
输出信号，尽量使用大电流、低阻抗的电偶跃迁驱动；对于刻度显示器，则可以使用大输出电压、高显示精度的电偶跃迁驱动；此外，在电机控制方面，可以根据电机的不同转速来选择不同的电偶跃迁驱动，如低、中、高速等。

此外，根据电偶跃迁驱动的类型，还可以再选择特定的电子器件，比如根据达
林顿调节的要求，可以使用电位器来调整跃迁速率；根据可控硅的需求，可以使用双极性稳压器等。

总之，选择电偶跃迁驱动时，要根据其应用领域和要求不同而选择适当的电偶
跃迁驱动，还要根据需要使用特定的电子器件，以满足科学技术的需求。

跃迁选择定则

跃迁选择定则

Ji = Jf + j, Jf + j -1, …, ⏐Jf - j⏐
对一定的多极辐射场j，原子分子初态和末态之间可能 取的角动量差为 ΔJ = ±j, ±(j-1), …, 0
由于跃迁速率随跃迁多极次 j 增加而迅速减少，一般情 况下只有最小极次j =∣Ji - Jf∣的辐射才能出现。如果它被 禁戒，则可出现下一极次的辐射。 光谱实验上能够观测到辐射除了电偶极辐射E1之外， 只有M1+E2和M2+E3的混合辐射。 由于j ≥ 1, 所以 0→0的跃迁是禁戒的。
2
式中Ei – Ef = hν，上式已对k和ε的各个方向取了平均，相当 于原子与各向同性的非偏振辐射的相互作用。
跃迁速率包括两项： 第一项对应于受激辐射，在通常光源作用下可以忽略，只有 在较强光场中才明显出现。 第二项对应于自发辐射，即外界不存在辐射 (nk,ε= 0)时的辐 射速率。 如果存在简并态，自发辐射的速率变为
. ..
5(1) 4(1) 3(1)
537.0 6675.2
. ..
5(2) 4(2) 3(2)
. ..
5(1) 4(1) 3(1)
. ..
5(2,1,0)
. ..
5(3,2,1) 4(3,2,1) 4(2,1,0) 3(3,2,1) 3(2,1,0)
5875.6
3(0)
538.9
2(0) 171129.148
λm1 1 μ ⎛ Z μ B ⎞ ⎛ Zα ⎞ −5 ≈ 2 ≈⎜ = ≈ 10 ⎟ ⎟ ⎜ λE1 c er ⎝ ea0 c ⎠ ⎝ 2 ⎠
2 2 2
电四极跃迁的跃迁速率与电偶极跃迁速率之比为
λE2 3 ⎛ ω r ⎞ 3 ⎛ Zα ⎞ −6 10 ≈ ⎜ = ≈ ⎜ ⎟ λE1 40 ⎝ c ⎟ 40 ⎝ 2 ⎠ ⎠

量子跃迁中的选择定则

量子跃迁中的选择定则

量子跃迁中的选择定则张扬威（华中师范大学物理学院2008级基地班，武汉，430079）摘 要 本文根据量子跃迁过程中遵从的角动量守恒和宇称守恒运用量子化概念，推导出电偶极近似条件下，在不同的外场中单电子原子以及多电子原子 辐射跃迁时的选择定则，并结合具体实例，说明这些规律的实质。

关键词 辐射跃迁 选择定则 角动量守恒 宇称守恒 原子态 电偶极近似 1 、 引言推微观粒子在不同的量子化状态间变化，称为跃迁。

跃迁有很多种，不同跃迁遵从不同的跃迁选择定则。

原子辐射跃迁的选择定则是原子能级之间发生跃迁所满足的条件，它对于研究光的吸收和发射具有很重要的意义。

由于电偶极矩跃迁强度比其它形式的跃迁强度大很多（倍），原子的辐射跃迁选择定则是指电偶极辐射跃迁选择定则。

它是从大量光谱的观察分析和研究中总结出来的，本文则运用量子力学的理论对它进行推导研究。

510~1082、 入射光为单色偏振光引入周期性微扰下的跃迁概率的基本知识：设微扰Hamilton 算符为（式中为与无关的厄米算符）'0(0)A cos ()(0)i t i t H t t F e e t ωωω∧∧∧−=<=+≥或 （1）体系在处于'0t =(0)n ϕ态， 跃迁到态的概率为't =t (0)m ϕ22(0)(0)2()()n m m mn m n W a t F E E πδω→==−±h h（2） 若该单色偏振光是沿x 轴 方向传播，偏振方向沿z 轴，在电偶极近似条件下，它的电场为0cos z t εεω= 0x ε= 0y ε= （3）电子的电偶极矩为 D er ex =−=−r（4）微扰作用势为 '00cos ()2i t i tz ez H D ez ez t e e ωωεεεεω∧−=−===+r uv （5） 对比（1）式可得 02ez F ε∧=（6） 带入（2）式可得 222(0)(0)0()2n m mn m n e W z E E πεδω→=−h h±（7）由（7）式可以得出，原子能否由n 态跃迁到m 态，决定于电子位矢的z 分量在这两个态之间的矩阵元mn z 是否为零。

跃迁规律

跃迁规律

2.5.5 跃迁选律内容更新如下：原子光谱是原子能级之间的跃迁产生的。

但在原子世界中, 这种跃迁也必须遵从某些规则, 并不是任何两个能级之间都可以随便跃迁。

这些规则就是所谓的“跃迁选律”。

允许的电偶极跃迁选律如下:ΔS = 0ΔL = 0，±1（但从L=0到L=0禁阻。

单电子原子基态为s态，L=0，对于它们来说，如果跃迁是ΔL = 0, 就只能从L=0到L=0, 而这是禁阻的。

因此，只有ΔL=±1）ΔJ = 0，±1（但从J=0到J=0禁阻）ΔMJ = 0，±1(但ΔJ = 0时, 从MJ= 0到MJ= 0禁阻)这些选律在轨道-自旋耦合作用变强时会逐渐失效, 而在j-j耦合方案中会变得完全不起作用。

因为在这种情况下，就连量子数L和S本身都已经越来越没有确定值，用量子力学的语言说，它们不再是好量子数。

所以, ΔS≠0的跃迁在轻原子中非常弱, 而在重原子中可能相当强，因为轨道-自旋耦合随原子序数的4次方增长。

此外, 原子都是中心对称的, 所以, 跃迁还要受到Laporte选律的限制。

为了搞清什么是Laporte选律, 首先需要知道谱项的宇称。

我们还记得, 原子轨道都有确定的宇称。

电子排布在轨道上形成组态, 进而确定了谱项, 所以, 谱项也有确定的宇称。

用下列两种方法的任意一种，很容易求出谱项的宇称:(1) 对于组态中各个电子的轨道角量子数l 求和，总和的奇偶性就等于该组态产生的所有谱项的奇偶性。

即: 总和若为偶数, 谱项的宇称为g; 总和若为奇数, 谱项的宇称为u 。

(2) 将组态中各个电子按所在轨道的宇称相乘(同样是，每个电子一项, 而不是每个轨道一项)，这种乘积叫做“直积”，所以使用特殊的乘号⊗。

乘法规则是：g ⊗g=u ⊗u=g , g ⊗u=u ⊗g=u 。

谱项的宇称为u 时，以O 作为右上标。

电偶极跃迁的Laporte 选律: 电偶极跃迁只能发生在宇称不同的态之间。

原子辐射跃迁的选择定则

原子辐射跃迁的选择定则

原子辐射跃迁的选择定则
原子辐射跃迁选择定则：
一、相对能量原则
1、“最小相对能量原则”
︰对对原子来说，跃迁发生时，原子总体上应处于原子态，其总能量也处于极小值。

2、“最大相对能量原则”：当一个原子发生跃迁时，它的总能量应达到最大值。

二、电子能量极值原则
1、“电子最小有效能原则”：在原子的转移过程中，释放的电子能量最小。

2、“电子最大有效能原则”：在原子的转移过程中，释放的电子能量最大。

三、电子数变化原则
1、“最小电子数多样性原则”：发生转移时，电子应达到最小多样性。

2、“最大电子数多样性原则”：发生转移时，电子应达到最大多样性。

四、电子的运动原则
1、“电子的最小运动原则”：发生跃迁时，电子的总运动量最小。

2、“电子的最大运动原则”：发生跃迁时，电子的总运动量最大。

五、保山詹原则
“保山詹原则”又称“纳米-山詹原则”，它声称：在原子发生跃迁时，电子应具有“最低穷到功率”，这表明，当跃迁发生时，电子应该具有最小的（穷到）动能。

综上所述，原子辐射跃迁的选择定则主要有：相对能量原则、电子能量极值原则、电子数变化原则、电子的运动原则和保山詹原则等。

这些定则共同控制电子跃迁的发生，体现出自然界量子物理学最基本的原理。

浅谈原子偶极跃迁选择定则

浅谈原子偶极跃迁选择定则

浅谈原子偶极跃迁选择定则原子偶极跃迁(APT)是一种量子效应，它是由Swedish Nobel Laureate Kai Siegbahn首先提出的，这种现象发生在激发态原子，也就是说，原子会在受到激光辐射时发生频率变换。

APT的特点是，当外加电场的强度变化时，原子的状态会发生变化，得到一系列特定频率的辐射。

而且，原子吸收的辐射能量只有在特定的频率时才能获得最大吸收力，这个特性使得APT有重要的应用价值。

原子偶极跃迁（APT）选择定则是指当原子在受到外加电场时，原子状态会发生变化，而变化后原子只能在特定的频率上吸收辐射。

这些特定的频率被称为APT选择定则。

APT选择定则可以用于控制原子辐射的吸收，从而实现微观的控制。

APT选择定则的物理本质是由发生结构性变化的原子长度、电场强度和温度三个要素决定的。

在非激发态下，原子是稳定的，只有在电场强度或温度发生变化时，原子才会发生改变，进入激发态。

而在激发态下，原子会在特定的频率上吸收辐射，从而实现微观的控制。

APT选择定则也可以用在X射线的应用中，由于X射线的能量更强，因此其产生的APT效应也更加明显。

X射线谱图可以显示吸收辐射的频率，从而进一步证明存在APT选择定则的存在。

比如，通过利用X射线谱图可以检测出特定元素的含量，进而用于病理学、化学等学科的研究。

此外，APT选择定则也可以用于原子分子发射谱（EM spectrum）的研究，通过研究不同原子及分子的发射谱，可以进一步探究激发态原子发射谱的APT选择定则，从而更深入地了解激发态原子及分子的特性。

既然原子偶极跃迁（APT）有着如此多的应用，我们就更应该去重视原子偶极跃迁（APT）的研究，也应该更加系统地去研究APT选择定则的影响因素，以证实未来可以更好地利用APT选择定则来优化实验结果。

综上所述，原子偶极跃迁（APT）选择定则是由原子状态改变、外加电场强度变化以及温度变化三个要素决定的，具有重要的应用价值，是控制原子辐射吸收的重要手段。

量子力学原子物理学选择定则光谱理论实验观察本质解释现象

量子力学原子物理学选择定则光谱理论实验观察本质解释现象

1
cosθYlm(θ,ϕ)
=
(l
+m+1)(l −m+1) (2l +3)(2l +1)

2
Yl+1,m
1
+
(l +m)(l −m) (2l −1)(2l +1)
2
Yl−1,m
1
sinθe±iϕYlm(θ,ϕ)
=
m
(l
±m (2l
+ +
2)(l ±m+1) 3)(2l +1)
(l +1): l
注 : 该分支比与初态磁量子数无关.跃迁到
l ' = l +1或l −1态的概率(对m'求和)也与m无关.
由选择定则知∆ l = l '−l = ±1,于是有
∑
l 'm' n lm
2
=1
m'
这个结果也可以利用Ylm的正交归一完备性导出:
∑
l 'm' n lm
2
=பைடு நூலகம்
∑
lm n l 'm'
l −1,m±1n lm 2 = (l m m)(l m m−1) 2(2l −1)(2l +1)
∑ l −1,m' n lm 2 = l
m'
2l +1
所以跃迁到终态m' = m+1,m,m−1的分支比:
(l −m)(l +m1): 2(l +m)(l −m):(l −m+2)(l −m+1)
11.用沿正z方向传播的右旋圆偏振光照射原 子,造成原子中电子的受激跃迁,求选择定则. 解: 对于右旋偏振光(振幅为2ε0)有
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
LS耦合：
0 ∆S = ∆L = 0, ±1 ∆J = 0, ±1 ( J = 0 → J = 0除外） ∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
jj耦合
∆j = 0, ±1 (跃迁电子） ∆J = 0, ±1 ( J = 0 → J = 0除外） ∆M = 0, ±1 (当∆J = 0时，M = 0 → M = 0除外) J J J
X射线不带电、很强的穿透性、直 线传播、使照相底片感光、使气 体电离奇特性质等。
The Nobel Prize in Physics 1901
§4.5原子的内层能级和特征X射线—X射线的波性 X射线是电磁波
晶体衍射 1912年，劳厄建议，鉴于晶体内部原子间距与X射 线的波长数量级相同，同时规则排列，可以当作 三维光栅，做晶体衍射实验。
(波长10-3 nm~1nm)
Max von Laue (1879 -1960)
实验：W. Friedrich, P. Knipping
劳厄斑
The Nobel Prize in Physics 1914
§4.5原子的内层能级和特征X射线—X射线的能谱
晶体衍射 1912年，小布拉格提出一种更简便的晶体衍射方法。 规则排列的原子形成布拉格平面，X射线从相邻平面 散射，形成干涉。
1 1 − 2 2 2 3
0.9
0.8
Lα线
L = ν R ( Z − 7.4) 2
Kα
0.7
Lα
0.6
Cr FeCu
0.5 20
Mo
40
W
Z
60
80
K线和L线的莫塞莱图
根据实验测量的特征线波数，从莫塞莱图上就可以标识元素的种类， 所以特征谱又称为标识谱。
§4.5原子的内层能级和特征X射线—X射线的能谱
K = ν R ( Z − 1) 2 1 1 − 2 2 1 2
1 1 − 2 2 2 3
L = ν R ( Z − 7.4) 2
特征X射线产生机制
§4.5原子的内层能级和特征X射线—X射线的能谱
选择定则：
跃迁电子要满足
∆l =±1
∆j = 0, ±1
§4.5原子的内层能级和特征X射线—俄歇电子能谱
轫致辐射(bremsstrahlung，刹车辐射)
hν= T − T ′
hν max=
hc
λmin
= T= eU
杜安(W. Duane)和亨特(P. Hunt)于1915年实验测定了h 值，与利用光电效应 实验测定的h值十分接近。
§4.5原子的内层能级和特征X射线—X射线的能谱 X射线特征谱
当加速电压大于一定值时，在连续谱 上出现了分立的线谱： (1) 其波长与加速电压无关，只与靶 材料有关，因此称为特征谱。
W. L. Bragg (1890-1971)
布拉格条件(相干加强)
2 = d sin θ n= λ , n 1, 2,3
W. H. Bragg (1862 -1942) 大布拉格的X射线分光仪 The Nobel Prize in Physics 1915
§4.5原子的内层能级和特征X射线—X射线的能谱 X光管发射的能谱
H. Moseley (1887-1915)
§4.5原子的内层能级和特征X射线—X射线的能谱
各元素的特征线波数的平方根与原子序数(原子核电荷数)成线性关系 莫塞莱经验公式 Kα线 (莫塞莱定律)
1.0
(1/λ)1/2 (m-1/2)
1 1 K = ν R ( Z − 1) 2 2 − 2 1 2
电偶极辐射的选择定则 (多电子原子情形) 拉波特定则：跃迁只允许在宇称相反的态之间发生。
在中心力场下，单电子的波函数为
unl ml (r ) = Rnl (r )Ylml (θ ,φ )
空间反演 r → -r
Otto Laporte
在球坐标下，这种反演变换为：
r→r θ → π −θ φ →π +φ
P. V. Auger (1899-1993)
K壳层出现一个空位后，一个L壳层s支壳层上的电 子 (2s 电子 )跃迁到 K 壳层填充这个空位，释放出的 能量传递给L壳层p支壳层上的一个电子(2p电子)并 使之电离，这一过程称为KLILII,III俄歇跃迁。 俄歇电子的动能
E A = EK − ELI − ELII ,III
§4.5原子的内层能级和特征X射线—俄歇电子能谱
电子碰撞产生的Ar原子LMM俄歇谱
§4.5原子的内层能级和特征X射线—荧光产额
1.0 0.8
K壳层
0.6
ω
0.4 0.2
L壳层 M壳层
0.0
0
20
40
60
80
100
原子序数
K壳层的荧光产额
KX 光子数 ωK = 有K 层空位的原子数
ωK ~ (1+bKZ-4)-1
(2) 不同的靶材料，除了波长不同外， X射线的特征谱具有相似的结构。
§4.5原子的内层能级和特征X射线—X射线的能谱
1913年，莫塞莱(H. G. J. Moseley)系统地测量了从铝到 金总共38种元素的特征谱。 发现特征谱包含两组谱线，按波长的次序称为： K线系：Kα、Kβ、Kγ 等谱线； L线系：Lα、Lβ、Lγ 等谱线。 原子序数大的元素会出现更多的谱系，分别称为M系，N系。
§4.4 多电子原子—多电子原子光谱—He原子光谱
基态：1s2 1S 单电子激发态：
1sns 1S 1snp 1P 1snd 1D 1snf
1F 3S 3P 3D 3F
氦原子的能级和相关的光谱跃迁
§4.5原子的内层能级和特征X射线—X射线的发现
1895年，伦琴发现了X射线
Wilhelm Röntgen (1845-1923)
bK ~7.5×105
§4.5原子的内层能级和特征X射线—荧光产额特征X射线—荧光产额 质子X荧光分析
径向函数不变，而角向的球谐函数有
Ylml (π − θ ,π + φ ) =− ( 1)l Ylml (θ ,φ )
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
单电子状态的宇称为
(-1)l
若 l 为偶数，则波函数在反演变换下不变，称该状态具有偶宇称。 若 l 为奇数，则波函数在反演变换下变号，称该状态具有奇宇称。 对于多电子原子，在中心力场近似下，原子的状态由电子组态描述，宇 称为：
li ∑ (−1)
在电偶极辐射中，光子带走的角动量为 ，由于宇称守恒，要求电偶极 跃迁的选择定则是
∆ ∑ li = ±1
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
一般情况下，原子光谱只涉及到单电子的跃迁 选择定则简化为
∆l =±1
氦原子的能级和相关的光谱跃迁
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
-
+
+
-
-
+
原子处在定态
激发电偶极振荡
辐射相同频率光子
跃迁速率
2 2 ω3 ω3 * λ= p= u (−er )ui dτ ≠ 0 fi 3 3 ∫ f 6ε 0 hc 6ε 0 hc
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则