跃迁类型和选择定则

原子发射光谱法是一种用于确定物质中元素组成的分析方法。

在这个过程中，原子从高能级跃迁到低能级时会发射出特定波长的光。

这些光的波长与元素的类型和浓度有关。

原子发射光谱法中的能级跃迁类型主要有以下几种：
1. 电子跃迁：这是最常见的能级跃迁类型。

当原子中的电子从一个能级跃迁到另一个能级时，会吸收或发射能量。

这种能量的吸收或释放通常以光子的形式发生，因此可以通过测量光的波长来确定元素的存在。

2. 核自旋跃迁：在某些情况下，原子核的自旋状态也会发生变化。

这种变化也会导致能量的吸收或释放，从而影响原子发射光谱。

3. 核外电子轨道跃迁：除了电子跃迁之外，原子核外的电子轨道也可能会发生跃迁。

这种跃迁通常发生在具有多个电子轨道的元素中，如过渡金属元素。

4. 离子化和去离子化：在某些情况下，原子可能会失去一个或多个电子，形成离子。

离子的形成和消失也会导致能量的吸收或释放，从而影响原子发射光谱。

5. 核反应：在某些极端条件下，原子核可能发生裂变或聚变反应，导致能量的释放。

这种能量的释放也会影响原子发射光谱。

跃迁矩阵元和选择定则跃迁矩阵元和选择定则是量子力学中重要的概念，可以用于描述原子或分子中电子能级之间的跃迁过程。

通过研究跃迁矩阵元和选择定则，我们可以深入理解量子系统的行为以及光谱的特性。

本文将介绍跃迁矩阵元和选择定则的概念和应用。

一、跃迁矩阵元的定义和性质在量子力学中，电子从一个能级跃迁到另一个能级需要通过一个跃迁矩阵元。

跃迁矩阵元描述了跃迁过程中的激发或退激发的强度，并对跃迁的速率和强度产生影响。

跃迁矩阵元的数值大小决定了跃迁的概率。

跃迁矩阵元可以表示为以下形式：M = ⟨f|V|i⟩其中|i⟩和|f⟩分别表示初态和末态，V表示相互作用势能。

跃迁矩阵元的计算通常需要涉及到波函数的积分运算，在具体计算中可以采用不同的近似方法，如非简并微扰理论或量子力学中的选择定则来简化计算过程。

跃迁矩阵元具有以下性质：1. 跃迁矩阵元是厄米矩阵，即M = M*，其中*表示共轭转置。

2. 跃迁矩阵元可能为零，这意味着某些跃迁是禁止的，即在特定条件下无法发生。

3. 跃迁矩阵元与波函数的对称性密切相关。

对称性分析可以帮助确定跃迁的强弱以及选择定则。

二、选择定则的概念和应用选择定则是用来判断某些跃迁是否允许的条件，即在特定的对称性或空间约束下，跃迁是否发生。

选择定则可以帮助我们理解光谱的特性，以及探索量子系统的性质。

1. 电偶极近似和选择定则在电偶极近似下，我们可以忽略其他高阶矩阵元的贡献，只考虑电偶极矩阵元的作用。

此时，选择定则可以简化为以下形式：Δl = ±1, Δm = 0, ±1其中Δl表示轨道量子数的变化，Δm表示磁量子数的变化。

根据这些选择定则，我们可以判断某些跃迁是否是禁止的，从而解释实验中观察到的光谱现象。

2. 选择定则的对称性分析除了电偶极近似外，我们还可以通过对称性分析来推导选择定则。

对称性分析可以基于空间取向、轴对称性或其他对称性进行处理。

通过对系统的对称性进行分析，我们可以判断某些跃迁是否被禁止。

1.自发跃迁（1）定义：处于较高能级的粒子自发地跃迁到较低能级上去的过程.（2）自发跃迁放出光子的能量等于高能级与低能级之间的能量差，即E=Em-En（m＞n）.放出光子的频率满足hν＝Em一En(多也不行，少也不行)，可以看出，原子发射光子的频率是分立的，不连续的原子只能发射一些特定频率的光子，能级差越大，放出光子的频率就越高。

由于不同的原子具有不同的结构，能级各不相同，因此辐射（或吸收）光子的频率也不相同，这就是不同元素的原子具有不同的特征谱线的原因.（3）氢原子能级跃迁的种类①大量的氢原子处在量子数为”的能级，向各低能级跃迁时，可能辐射光子的频率有N＝Cₙ²＝n(n-1)/2种.②一个处于激发态的氢原子向基态跃迁时，最多可以辐射n-1种频率的光子.2.受激跃迁受激跃迁是原子吸收能量从低能级向高能级的跃迁.使原子能级跃迁的粒子有两种：光子和实物粒子（1）原子吸收光子的受激跃迁原子若是吸收光子的能量而被激发，吸收光子的能量必须恰好等于两能级间的能量差，否则不被吸收，即原子只能吸收一些特定频率的光子，不存在激发到＝2能级时的能量有余，而激发到＝3能级时能量不足的问题，这也是为什么原子吸收光谱的频率与发射光谱的频率相同的原因.（2）原子吸收外来实物粒子的能量的受激跃迁原子还可以由于实物粒子的撞击而被激发.由于实物粒子的动能在碰撞时可以全部或部分被原子吸收，所以只要人射粒子的能量大于或等于两能级的能量差值（E≥E一E），原子只吸收恰为两能级间能量差的部分，从而可使原子发生能级跃迁.3.原子的电离若入射光子的能量或者与原子碰撞的实物粒子在碰撞过程中损失的能量大于或等于原子从低能级到n→∞的激发态所需的能量，也可以被原子吸收，使原子电离，大于电离能的那部分能量成为自由电子的动能.☞跃迁与电离1.hν＝Em-En，只适用于光子和原子作用，使原子在各定态之间跃迁的情况，对于光子和实物粒子撞击使原子电离的情况，则不受此条件的限制。

d-d跃迁选择规则
d-d跃迁是指在过渡金属化合物中，由于电子在d轨道之间的跃迁而引起的吸收或发射光谱。

对于d-d跃迁，存在一些选择规则，它们决定了哪些跃迁是可能的，而哪些是被禁止的。

这些选择规则包括：
1.洪特规则（Hund's Rule）：洪特规则指的是在d轨道中的电子
首先填充未成对的轨道，然后再填充成对的轨道。

在d-d跃迁
中，通常只有那些未成对的电子可以参与跃迁。

2.电子转移的选择规则：d-d跃迁通常涉及到电子从一个d轨道
跃迁到另一个d轨道。

在这个过程中，电子的自旋必须保持不
变。

这意味着电子不能发生自旋反转。

3.轨道重叠：轨道之间的重叠也是选择规则的一个重要方面。

如
果两个轨道之间的重叠很小，那么相关的d-d跃迁可能是禁止
的。

4.对称性规则：对称性也是影响d-d跃迁的选择规则之一。

如果
跃迁引起的分子轨道对称性的改变，可能导致跃迁的禁止。

需要注意的是，这些选择规则并非绝对的，一些跃迁可能在特定条件下仍然发生，但这些规则提供了一些有用的指导原则，帮助解释和预测d-d跃迁的性质。

物理跃迁知识点总结一、原子能级能级的理论是量子力学的基础之一。

在原子系统中，能级是指原子处于不同能量状态下的可能性。

原子的能级是通过求解薛定谔方程得到的。

在原子内，能级通常用量子数来标识，每个能级有自己的能量和波函数。

电子在原子中的能级结构决定了原子的光谱和其他性质。

在原子的能级结构中，跃迁是电子从一个能级跳跃到另一个能级的过程。

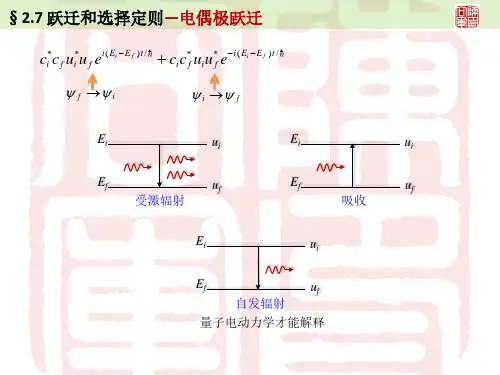
二、原子跃迁的分类在原子的能级结构中，跃迁可以分为受激辐射跃迁、自发辐射跃迁和受激吸收跃迁三种类型。

1. 自发辐射跃迁自发辐射跃迁是指原子由高能级向低能级跃迁并释放出光子的过程。

这种跃迁是由于原子内部的不稳定性而导致的，它是一种自发性的现象。

自发辐射跃迁是产生光谱辐射的主要机制之一。

2. 受激辐射跃迁受激辐射跃迁是指原子在外界光子的作用下，由低能级向高能级跃迁并且吸收入射光子能量的过程。

这种跃迁需要外界的激发光子来提供能量，因此称为受激辐射。

受激辐射跃迁是激光原理的基础之一。

3. 受激吸收跃迁受激吸收跃迁是指原子处于高能级时，由外界光子的作用下，向更高的能级跃迁并吸收入射光子能量的过程。

这种跃迁需要外界光子提供能量，并且会增强入射光子的强度。

三、原子跃迁的选择定则原子跃迁的选择定则是描述原子在跃迁过程中遵循的守恒规律，它是由旋转和电荷守恒、动量守恒和角动量守恒等物理原理决定的。

1. 电偶极辐射选择定则电偶极辐射选择定则是对原子在跃迁时电偶极辐射的强度和方向的规定。

根据电偶极辐射选择定则，两个能级间的跃迁只在它们的角动量量子数或自旋量子数相差一个单位时才会发生电偶极辐射。

2. 磁偶极辐射选择定则磁偶极辐射选择定则是对原子在跃迁时磁偶极辐射的强度和方向的规定。

磁偶极辐射只在原子的轨道角动量量子数改变一个单位时才会发生。

四、光谱光谱是原子和分子在受到外界激发时辐射出的光线。

根据辐射光的特点，光谱可以分为连续光谱和线状光谱。

连续光谱是指在原子或分子受激发时产生的由连续波长的光线组成的谱线。

原子结构知识原子能级跃迁的角动量选择定则原子能级跃迁的角动量选择定则是量子力学中描述原子中电子从一个能级跃迁到另一个能级时，其角动量的限制条件。

这个选择定则是由斯腾格尔定则和禁戒规则共同决定的。

首先，让我们来了解一下斯腾格尔定则（Stemler rule）。

斯腾格尔定则是根据经典物理学中的角动量守恒定律得出的。

它表明电子跃迁前后的总角动量守恒，即电子跃迁前后的总角动量矢量的大小和方向不变。

根据斯腾格尔定则，如果电子在一些能级跃迁时，它的总角动量发生变化，那么该能级的两个子能级的总角动量矢量之和应该等于电子跃迁前的总角动量矢量。

接下来，让我们来了解一下禁戒规则。

禁戒规则是指一些特定的跃迁过程在光谱中表现为禁止的现象。

其中最著名的禁戒规则是电偶极辐射选择定则。

这个选择定则是指电子跃迁时，只有在电偶极矩变化的过程中，能级之间的跃迁才可能发生。

根据电偶极辐射选择定则，电子从一个能级跃迁到另一个能级时，二者之间的跃迁必须满足△l=±1，△m=0,±1、其中，l是轨道角动量量子数，m是角动量的磁量子数。

综合斯腾格尔定则和禁戒规则，我们可以得出原子能级跃迁的角动量选择定则。

根据角动量守恒定律，电子跃迁前后的总角动量矢量之和应该守恒。

根据禁戒规则，这个总角动量矢量之和应该满足△l=±1，△m=0,±1、这意味着电子跃迁必须满足这些限制条件。

举个例子来说明角动量选择定则。

考虑一种跃迁过程，电子从一个s 轨道上的n=1能级跃迁到p轨道上的n=2能级。

根据斯腾格尔定则，总角动量矢量的大小和方向在跃迁前后是守恒的。

在这个过程中，n=1能级只有一个s轨道，它的轨道角动量量子数l=0，磁量子数m=0。

而n=2能级有三个p轨道，其轨道角动量量子数l=1，磁量子数m可以取-1，0，1三个值。

根据禁戒规则，△l=±1，△m=0,±1、因此，电子跃迁时，只有可能从n=1的s轨道跃迁到n=2的三个p轨道中的一个，且总角动量守恒。

第三章 理想晶体带间光跃迁总体系：光子+电子+声子()()()(),(),n X n λλψΘ=Ξ=ΞψR R R r r3.1 直接跃迁--速率和选择定则电子-声子相互作用可忽略的情形：单由光子-电子相互作用引起的没有声子参与的光跃迁跃迁初末态就不必标记其 声子状态 ()q X n =R初态 ,iiiii i n n κκψ≡Θ==ψ 跃迁到末态 ,f ffff f n n κκψ≡Θ==ψ跃迁速率：归结为计算相互作用哈密顿量在跃迁初末态之间的矩阵元。

费米黄金规则：()22fi If i fiW H E E πδ=- （3.1-1）在一级近似下（单光子跃迁），弱辐射场与原子体系（其中的电子体系）相互作用哈密顿量I H 近似为：()()()()()1=I I i i i iie i iiH H e m A r p e m A r p ≈=-⋅⋅∑∑其中()i A r 为相关的光场(模式κ)的矢势如（1.2-7），（1.2-9），（1.2-10）所示跃迁速率：(一阶微扰)正比于初末电子态 iψ和fψ间(1)I H 的矩阵元的平方，即()2exp fifii i i ee W i r p m κκψπψ±⋅⋅∑k(3.1-2)初末电子态 i ψ和f ψ：相应电子组态的行列式波函数绝热近似，单电子近似和能带近似→ 理想晶体电子态的能带图像理想晶体的带间（直接）光跃迁是光与电子体系相互作用导致的，在两个电子组态（相应的波函数为行列式波函数）间的跃迁上述矩阵元的性质：注意：微扰哈密顿算符()()()1=II e i i iH H e m A r p ≈⋅∑是单电子算符之和，它具有如下的一般形式：ˆˆ()NiG gi =∑ （3.1-3）其中右边求和式中的每一项ˆ()gi 都只与某一个电子i 的坐标有关，其形式不随i 而变 -→算符ˆG对电子的交换是对称的下面我们先讨论算符G 的矩阵元的性质，然后由此推断出几个跃迁选择定则。

氢原子光谱的实验规律氢原子光谱的实验规律是原子光谱学中的重要内容，通过对这些规律的研究，我们可以深入了解氢原子的结构和性质。

以下是氢原子光谱的实验规律：1.光谱线系的规律性：氢原子光谱是由一系列具有特定波长的线组成的线系。

这些线按照波长的顺序排列，形成光谱的各个部分，如赖曼系、巴尔末系等。

这些线系的分布和排列都遵循着一定的规律，反映了氢原子能级的变化规律。

2.波长与能级的关系：氢原子光谱的波长与氢原子的能级有关。

根据玻尔的原子模型，当氢原子从较高能级跃迁到较低能级时，会释放出一定频率的光子，其波长与能级差有关。

因此，通过对光谱线的波长进行测量和分析，可以推导出氢原子的能级结构。

3.谱线强度与能级能量差的关系：氢原子光谱的强度与氢原子的激发态和基态之间的能量差有关。

能量差越大，从激发态跃迁到基态时释放的光子能量越高,谱线的强度越强。

因此,通过对光谱线强度的测量和分析，可以了解氢原子不同能级之间的能量差。

4.跃迁选择定则：根据量子力学原理，氢原子在发生能级跃迁时，只能选择满足选择定则的跃迁方式。

这些选择定则规定了不同能级之间跃迁的条件，包括允许和禁戒跃迁。

通过对谱线的观察和分析，可以了解这些选择定则的具体表现。

5.光谱精细结构：氢原子光谱除了具有主线系外，还有许多细分的结构，称为光谱的精细结构。

这些精细结构是由量子力学中的自旋-轨道耦合作用引起的，它们的观察和分析可以帮助我们深入了解氢原子的内部结构和性质。

6.实验手段的多样性：为了获得更准确和详细的光谱数据，实验上采用了多种手段和技术，如光谱仪的改进、高精度测量技术的运用、激光光谱等。

这些技术和手段的应用，使得我们可以更深入地研究和了解氢原子光谱的规律和机制。

综上所述，氢原子光谱的实验规律是研究原子结构和性质的重要手段之一。

通过对这些规律的研究和分析，我们可以深入了解原子能级结构、能级跃迁类型、跃迁选择定则等方面的问题，为量子力学和原子物理学的发展提供重要的实验依据。

量子跃迁中的选择定则张扬威（华中师范大学物理学院2008级基地班，武汉，430079）摘 要 本文根据量子跃迁过程中遵从的角动量守恒和宇称守恒运用量子化概念，推导出电偶极近似条件下，在不同的外场中单电子原子以及多电子原子 辐射跃迁时的选择定则，并结合具体实例，说明这些规律的实质。

关键词 辐射跃迁 选择定则 角动量守恒 宇称守恒 原子态 电偶极近似 1 、 引言推微观粒子在不同的量子化状态间变化，称为跃迁。

跃迁有很多种，不同跃迁遵从不同的跃迁选择定则。

原子辐射跃迁的选择定则是原子能级之间发生跃迁所满足的条件，它对于研究光的吸收和发射具有很重要的意义。

由于电偶极矩跃迁强度比其它形式的跃迁强度大很多（倍），原子的辐射跃迁选择定则是指电偶极辐射跃迁选择定则。

它是从大量光谱的观察分析和研究中总结出来的，本文则运用量子力学的理论对它进行推导研究。

510~1082、 入射光为单色偏振光引入周期性微扰下的跃迁概率的基本知识：设微扰Hamilton 算符为（式中为与无关的厄米算符）'0(0)A cos ()(0)i t i t H t t F e e t ωωω∧∧∧−=<=+≥或 （1）体系在处于'0t =(0)n ϕ态， 跃迁到态的概率为't =t (0)m ϕ22(0)(0)2()()n m m mn m n W a t F E E πδω→==−±h h（2） 若该单色偏振光是沿x 轴 方向传播，偏振方向沿z 轴，在电偶极近似条件下，它的电场为0cos z t εεω= 0x ε= 0y ε= （3）电子的电偶极矩为 D er ex =−=−r（4）微扰作用势为 '00cos ()2i t i tz ez H D ez ez t e e ωωεεεεω∧−=−===+r uv （5） 对比（1）式可得 02ez F ε∧=（6） 带入（2）式可得 222(0)(0)0()2n m mn m n e W z E E πεδω→=−h h±（7）由（7）式可以得出，原子能否由n 态跃迁到m 态，决定于电子位矢的z 分量在这两个态之间的矩阵元mn z 是否为零。

原子辐射跃迁的选择定则
原子辐射跃迁选择定则：
一、相对能量原则
1、“最小相对能量原则”
︰对对原子来说，跃迁发生时，原子总体上应处于原子态，其总能量也处于极小值。

2、“最大相对能量原则”：当一个原子发生跃迁时，它的总能量应达到最大值。

二、电子能量极值原则
1、“电子最小有效能原则”：在原子的转移过程中，释放的电子能量最小。

2、“电子最大有效能原则”：在原子的转移过程中，释放的电子能量最大。

三、电子数变化原则
1、“最小电子数多样性原则”：发生转移时，电子应达到最小多样性。

2、“最大电子数多样性原则”：发生转移时，电子应达到最大多样性。

四、电子的运动原则
1、“电子的最小运动原则”：发生跃迁时，电子的总运动量最小。

2、“电子的最大运动原则”：发生跃迁时，电子的总运动量最大。

五、保山詹原则
“保山詹原则”又称“纳米-山詹原则”，它声称：在原子发生跃迁时，电子应具有“最低穷到功率”，这表明，当跃迁发生时，电子应该具有最小的（穷到）动能。

综上所述，原子辐射跃迁的选择定则主要有：相对能量原则、电子能量极值原则、电子数变化原则、电子的运动原则和保山詹原则等。

这些定则共同控制电子跃迁的发生，体现出自然界量子物理学最基本的原理。

5.33讲稿: 电子光谱法电子光谱法: 利用光吸收来改变分子中电子的电荷分布（大量的能量：通常可使键断开）平衡时，分子处于电子基态→最低电子能态，即v=0。

通过v，J的改变跃迁到高的电子能态 选择定则 — 即使对于双原子, 它也会很复杂→ 核/自旋/总角动量守恒(对更大的分子：很难预测)。

再吸收要求 0q μ∂≠∂ → 奇偶改变：u ↔ g , 轨道反对称性的改变。

电子跃迁类型有机物: 包括π， σ， n 电子饱和化合物σ→σ* , n →σ* : 远紫外 (<250 nm)双键/不饱和系统—到π*轨道的跃迁所需能量相对较低π→π*, n →π* 跃迁 ：紫外和可见(200-700 nm)无机: 另外,d 轨道在配位体存在下的发生分裂，分裂轨道间的跃迁。

d-d 跃迁电荷转移：在配体和金属之间的电子转移。

一个授电子而另一个受电子－MnO4双原子体系的电子光谱• 振动和转动结构也有电子吸收。

• 较为典型的是v=0基态电子, 跃迁到不同v值的激发态。

• 激发伴随着振动激发，激发态的回复力。

电子跃迁: 弗兰克康登原理 (垂直跃迁):电子比核运动得快得多，因此激发过程不会引起核的几何变化。

激发态表面:游离或排斥态(反键作用) →离解成原子(H2 的A状态)2）束缚态—成键轨道—束缚态是稳定的能量最小值点(通常导致较大的核位移)(H2 的B状态)(对双原子体系: 基态 =X; 激发态= A, B, C . . .)激发态是非谐性的—表面必须允许原子离解，对于高的激发态振动距离⊿v将减小。

‘从0－0的跃迁和收敛极限→得到Do因为T+ D o‘= D o+⊿E atomicE如果知道⊿E atomic，你能得出D o强度： 跃迁几率由弗兰克康登原理决定最可能的激发是经典旋转。

“选择定则”是弗兰克康登重叠积分→ '''*()()v v R R dR ΨΨ∫ …此强度可以给出r比r e ‘: 位移。