两平面的平行的判定和性质
- 格式:docx
- 大小:271.61 KB
- 文档页数:19



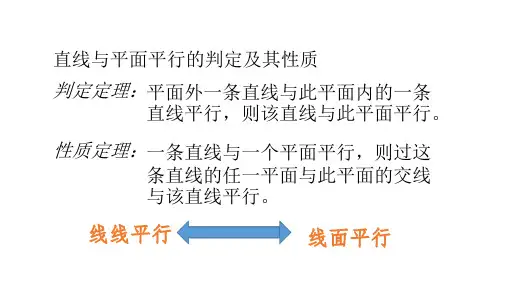
平行1.直线与平面平行的判定(1)直线与平面平行的定义:如果一条直线与一个平面没有公共点,我们就说这条直线与这个平面平行.(2)直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.符号表示为:.注意:这个定理是证明直线与平面平行最常用的一个定理,也就是说欲证明一条直线与一个平面平行,一是说明这条直线不在这个平面内,二是要证明已知平面内有一条直线与已知直线平行.2.两个平面平行的判定(1)两个平面平行的定义:两个平面没有公共点,则两个平面平行.(2)平面与平面的平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.符号表示为:.注意:这个定理的另外一种表达方式为“如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行,那么这两个平面平行”.(3)平行于同一平面的两个平面互相平行.即.3.直线与平面平行的性质(1) 直线与平面平行的性质定理:一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.符号表示为:.注意:如果一条直线和一个平面平行,那么这条直线和平面内的无数条直线平行,但不能误解为“如果一条直线与一个平面平行,那么这条直线就和平面内的任意一条直线平行”.(2)直线与平面平行的性质:过平面内一点的直线与该平面平行的一条直线平行,则这条直线在这个平面内.符号表示为:若,点,且,则.4.平面与平面平行的性质(1)如果两个平面平行,那么其中一个平面内的任意直线均平行与另一个平面.此结论可以作为定理用,可用来判定线面平行.(2)两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.(3)夹在两个平行平面间的平行线段相等.垂直1.直线与平面垂直的判定(1)直线与平面垂直的定义如果一条直线和一个平面内的任意一条直线都垂直,我们就说这条直线和这个平面垂直,其中直线叫作平面的垂线,平面叫作直线的垂面.注意:①定义中的“任意一条直线”和“所有直线”是同义语,不能改成“无穷多条直线”.②如果或,那么直线l不可能与平面内的任意一条直线都垂直.由此可知,当时,直线l和一定相交,它们唯一的交点叫做垂足.(2)直线和平面垂直的判定定理如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直与这个平面.(3)关于垂直的存在唯一性命题1:过一点有且只有一条直线和已知平面垂直.命题2:过一点有且只有一个平面和已知直线垂直.2.平面与平面垂直的判定(1)平面与平面垂直的定义:两个平面相交,如果所成的二面角是直二面角,则称这两个平面互相垂直.(2)两个平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直. 符号表示为:.3.直线与平面垂直的性质如果两条直线同垂直于一个平面,那么这两条直线平行. 符号表示:. 作用:可作线线平行的判定定理. 4.平面与平面垂直的性质(1)两个平面垂直的性质定理如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面. 符号表示为:.(2)如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面. (3)三个两两垂直的平面的交线两两垂直.(4)如果两个平面垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内.空间几何定理公理总结:1.平面的基本性质公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点,有且只有一个平面. 推论1 经过一条直线和这条直线外一点,有且只有一个平面. 推论2 经过两条相交直线,有且只有一个平面. 推论3 经过两条平行直线,有且只有一个平面. 公理4 同平行于一条直线的两条直线互相平行。



两平面平行的判定方法平面几何中,两平面平行是重要的概念,因为它涉及到许多实际问题,例如建筑、地图制作和制造业。
在本文中,我们将讨论10种不同的方法来判断两个平面是否平行,并提供详细说明。
1. 平行线性质法确定两个平面是否平行的最简单方法之一是检查它们所包含的直线。
如果两个平面包含两组平行直线,则这两个平面平行。
这被称为平行线性质。
平面上的平行线永远不会相交,而它们的距离始终相等。
2. 夹角相等法两个平面平行的另一种方法是它们的夹角相等。
当两个平面之间的夹角相等时,它们被认为是平行的。
这里需要注意的是,夹角是指两个平面的法线之间的角度。
3. 垂线判定法如果一条直线是第一个平面上的一条直线,并且以该直线垂直于第二个平面,则第一个平面和第二个平面是平行的。
垂线判定法基于这个原理。
这可通过将两个平面移到同一位置并在它们之间引入垂线来证明。
4. 辅助平面法辅助平面法是一种使用第三平面来判断两个平面平行的方法。
如果两个平面与第三个平面平行,则它们彼此平行。
该方法特别适用于设计要求多个平面平行的情况,例如构建多层建筑物。
5. 截线判定法如果一条直线是第一个平面和第二个平面上的两条直线的截线,则这两个平面平行。
截线判定法基于这个概念。
如果相交的两条线都是平面上的同一直线的截线,则这两个平面平行。
6. 倾斜角相等法倾斜角相等法是一种快速确定两个平面是否平行的方法。
如果两个平面的倾斜角相等,则这两个平面是平行的。
这种方法只能用于倾斜角相等的情况。
7. 向量法向量法是另一种判断两个平面是否平行的方法。
如果两个平面的法线向量相同,则它们是平行的。
将两个平面的向量相减,如果它们的值为零,则它们平行。
8. 距离法距离法是判断两个平面平行的一个简单方法,它基于平面之间的平行线性质。
如果两个平面的法线距离相等,则这两个平面平行。
用法线测量两个平面之间的距离,以确定它们是否平行。
9. 投影法投影法可以通过平面上点的投影来确定两个平面是否平行。

平面与平面平行的判定和性质第一章:教案简介本章将介绍教案平面与平面平行的判定和性质。
通过本章的学习,学生将能够理解并应用平面与平面平行的判定条件,掌握平面与平面平行的性质,并能够运用这些知识解决实际问题。
第二章:平面与平面平行的判定1. 判定条件一:如果两个平面的法向量互相平行,则这两个平面平行。
2. 判定条件二:如果一个平面经过另一个平面的法向量,则这两个平面平行。
3. 判定条件三:如果两个平面相交于一条直线,且这条直线垂直于两个平面的法向量,则这两个平面平行。
第三章:平面与平面平行的性质1. 性质一:平面与平面平行时,它们的法向量互相平行。
2. 性质二:平面与平面平行时,它们的法向量垂直于它们的交线。
3. 性质三:平面与平面平行时,它们的交线平行于它们的法向量。
第四章:应用举例1. 例一:给定两个平面,如何判断它们是否平行?2. 例二:给定一个平面和一条直线,如何判断这条直线是否与平面平行?3. 例三:给定两个平面和它们的交线,如何判断这两个平面是否平行?第五章:练习题1. 判断题:如果两个平面的法向量互相垂直,则这两个平面平行。
(对/错)2. 判断题:如果一个平面经过另一个平面的法向量,则这两个平面平行。
(对/错)3. 判断题:如果两个平面相交于一条直线,且这条直线垂直于两个平面的法向量,则这两个平面平行。
(对/错)4. 应用题:给定两个平面,它们的法向量分别为向量A和向量B。
判断这两个平面是否平行,并说明理由。
5. 应用题:给定一个平面P和一条直线L。
已知平面P的法向量为向量A,直线L的方向向量为向量B。
判断直线L是否与平面P平行,并说明理由。
第六章:教案平面与平面平行的判定和性质的综合应用1. 综合应用一:如何判断一个平面是否平行于另一个平面的交线?2. 综合应用二:如何判断一条直线是否与另一个平面平行?3. 综合应用三:如何判断两个平面是否平行,并确定它们的交线?第七章:教案平面与平面平行的判定和性质的证明题1. 证明题一:已知平面P和Q,证明平面P与平面Q平行的条件是它们的法向量互相平行。

空间几何中的平面平行在空间几何中,平行是一个重要的概念。
平行线在平面几何中常常被提及,但在空间几何中,平行的概念同样适用于平面。
本文将讨论空间几何中的平面平行的性质、判定方法以及应用。
一、平面平行的性质在空间几何中,两个平面可以相交,也可以平行。
如果两个平面相交于一条直线,则我们称这两个平面为相交平面;如果两个平面之间没有任何交点,我们称这两个平面为平行平面。
平面平行具有以下性质:1. 平行平面永远不会相交。
即使延长两个平面,它们也不会相交。
2. 平行平面中的任意一条直线都与两个平面平行,且平行于这两个平面的所有直线都互相平行。
3. 平行平面之间的距离在整个平面中都是相等的。
二、平面平行的判定方法在空间几何中,如何判定两个平面是否平行?下面介绍两种常见的判定方法。
1. 根据平面的法向量:平行的两个平面的法向量相等或相反。
对于一个平面,它有无穷多个垂直于其的向量,其中一个被称为法向量。
两个平面平行的充分必要条件是它们的法向量相等或相反。
通过计算平面的法向量,可以判断两个平面是否平行。
2. 根据两个平面上的直线关系:两个平面平行,其中一个平面上的一条直线与另一个平面上的一条直线平行。
在一个平面上取一条直线L,如果这条直线与另一个平面中的任意一条直线既不相交,也不平行,那么这两个平面就是平行的。
这个方法可以通过判断直线和平面的交点或者直线和平面的夹角来进行判定。
三、平面平行的应用平行平面在日常生活和工程应用中具有广泛的应用。
以下是一些实际应用的例子:1. 建筑设计在建筑设计中,平行平面的概念被广泛应用于各种结构,比如墙面、地面、天花板等。
平行平面的合理运用可以使建筑结构更加稳定,提高施工效率。
2. 制造业在制造业中,平行平面的测量和判定被广泛应用于加工、装配和检测等环节。
通过确保平行平面的准确度,可以实现零件的互换性和装配精度。
3. 交通工程在交通工程中,平行平面的概念用于道路设计和车辆行驶。
例如,在高速公路设计中,平行平面的正确运用可以提高道路车辆的安全性和舒适度。

两个平面平行的性质定理与结论:(面面平行→线线平行)②如果两个平面平行,那么某一个平面内的直线与另一个平面平行。
(面面平行→线面平行)面面平行的判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行(线面平行⇒面面平行)面面平行的判定方法:①面面平行的定义:两个平面无公共点。
②判定定理:////a b a b a b Pββαα⊂⊂⋂= ⇒ //αβ平面与平面平行的判定练习一、选择题;1.设直线l,m,平面α,β,下列条件能得出α∥β的有 ( )①l ⊂α,m ⊂α,且l ∥β,m ∥β;②l ⊂α,m ⊂α,且l ∥m ;③l ∥α,m ∥β,且l ∥mA 1个B 2个C 3个D 0个2. 已知:命题:P :α内存在着不共线的三点到平面β的距离均相等;命题:Q :α∥β,则下面成立的是( )A P ⇒Q ,P ⇐QB P ⇐Q ,P ⇒QC P ⇔Q ,D P ⇒Q , P ⇐Q3.下列命题中,可以判断平面α∥β的是( )①α,β分别过两条平行直线;②a ,b 为异面直线,α过a 平行b ,β过b 平行a ;A ①B ②C ①②D 无4.下列命题中为真命题的是( )A 平行于同一条直线的两个平面平行B 垂直于同一条直线的两个平面平行C 若—个平面内至少有三个不共线的点到另—个平面的距离相等,则这两个平面平行.D若三条直线a、b、c两两平行,则过直线a的平面中,有且只有—个平面与b,c都平行.5.下列命题中正确的是( )①平行于同一直线的两个平面平行;②平行于同一平面的两个平面平行;③垂直于同一直线的两个平面平行;④与同一直线成等角的两个平面平行A ①②B ②③C ③④D ②③④二、填空题;6.下列命题中正确的是(填序号);①一个平面内两条直线都平行于另一个平面,那么这两个平面平行;②如果一个平面内任何一条直线都平行于另一个平面,那么这两个平面平行;③平行于同一直线的两个平面一定相互平行;④如果一个平面内的无数多条直线都平行于另一个平面,那么这两个平面平行;7.若夹在两个平面间的三条平行线段相等,那么这两个平面的位置关系是;8.如右图,点P是光源,将投影片放在平面α内,问投影幕所在平面β与平面α______时,投影图象的形状不发生变化.三、解答题;9.平面α∥平面β,AB,CD是异面直线,M,N分别是AB,CD的中点,且A1∈α,BD∈β,求证:MN∥α.10.已知四面体ABCD中,M,N分别是△ABC和△ACD的重心,P为AC上一点,且AP:PC=2:1,求证:(1)BD∥面CMN;(2)平面MNP//平面BCD.11.在棱长为a的正方体ABCD—A1B1C1D1中,求证:平面A1BD∥平面CB1D1;。

空间几何中的平面平行关系在空间几何学中,平面平行关系是一个重要的概念。
当两个平面永远不相交,无论它们延伸到无穷远,都不会相交,我们就可以说这两个平面是平行的。
平面平行关系有一些性质和判定方法,本文将对这些内容进行详细讨论。
一、定义和性质1. 定义:如果两个平面不相交,则它们是平行的。
2. 性质:a. 平行的平面在任意方向上的截线是平行线。
b. 平面平行关系是对称关系,即如果平面A与平面B平行,则平面B与平面A也平行。
c. 平面平行关系是传递关系,即如果平面A与平面B平行,平面B与平面C平行,则平面A与平面C也平行。
二、平面平行的判定方法1. 通过两个平面的法向量判定:如果两个平面的法向量是平行的,则这两个平面平行。
2. 通过平面上的一组向量判定:如果两个平面上的相同向量比值相等,则这两个平面平行。
3. 通过平面上的直线与另一平面的交点判定:如果一条直线与一个平面平行于另一个平面,则这两个平面平行。
三、平行平面的性质和相关定理1. 平行平面的截距:平行平面的任意两个截距之比相等。
2. 平行平面的夹角:平行平面之间的夹角等于它们的法向量夹角的余角。
3. 平行线与平面的垂直关系:如果一条直线平行于一个平面,那么该直线上的任意一条直线都与该平面垂直。
4. 平行平面的平行线:平行平面上的平行线在空间中保持平行关系。
根据上述性质和判定方法,我们可以在空间几何中确定两个平面之间的平行关系。
在实际生活中,平面平行关系有广泛的应用,比如建筑设计、地理测量等领域都需要考虑平面平行关系。
理解和掌握平行关系的概念和判定方法对于解决实际问题非常重要。
总结:空间几何中的平面平行关系是一种重要的关系概念,具有一定的性质和判定方法。
理解和应用平面平行关系对于解决各种实际问题以及在相关领域中的应用具有重要意义。
通过本文的介绍,希望读者能够对平面平行关系有更深入的理解,并能够灵活应用于实际问题中。
典型例题一例1:已知正方体ABCD - A1B1C1D1. 求证:平面AB1D111平面C1BD . 证明:T ABCD - A1B1C1D1为正方体,••• D1A//C1B ,又C1B 平面C1BD , 故D1A// 平面C1BD .同理D1B1 //平面C1BD .又D1A D1B1 D1 ,•••平面AB1D1// 平面C1BD .说明:上述证明是根据判定定理1实现的.本题也可根据判定定理2证明,只需连接AC 即可,此法还可以求出这两个平行平面的距离.典型例题二例2:如图,已知// , A a, A求证:a .证明:过直线a作一平面,设b .•/ //••• a1 // b又a//• a//b在同一个平面内过同一点A有两条直线a,a1与直线b平行• a与a1重合,即a说明:本题也可以用反证法进行证明.典型例题三例3:如果一条直线与两个平行平面中的一个相交,那么它和另一个也相交.已知:如图,// ,1 A.求证:I与相交.证明:在上取一点B,过I和B作平面,由于与a有公共点A , 与有公共点B .•••与、都相交.设a, b .•/ //• a//b又I、a、b都在平面内,且I和a交于A .T I与b相交.所以I与相交.典型例题四例4:已知平面// , AB , CD 为夹在a ,间的异面线段,E、F分别为AB、CD的中点.求证:EF〃, EF // .证明:连接AF并延长交于G .••• AG CD F• AG , CD确定平面,且DG .•/// ,所以AC//DG ,ACF GDF ,又AFC DFG , CF DF ,••• △ ACF ◎△ DFG •••• AF FG •又AE BE ,• EF//BG, BG •故EF // •同理EF //说明:本题还有其它证法,要点是对异面直线的处理.典型例题六例6如图,已知矩形ABCD的四个顶点在平面上的射影分别为A1、B1、G、D1,且A、B i、C i、D i互不重合,也无三点共线. 求证:四边形A i B i C i D i是平行四边形.证明:T AA , DD i•- AA // DD i不妨设AA和DD i确定平面 . 同理BB i和CC i确定平面又AA i // BB i,且BB i• AA //同理AD //又AA i AD A//A D i,B iC i同理 AB 〃C i D i ••••四边形 ABQ i D i 是平行四边形.典型例题七m//1,所以m ,又T m , • // •选项D 也是错误的,满足条件的可能与 相交.答案:C说明:此题极易选A ,原因是对平面平行的判定定理掌握不准确所致.本例这样的选择题是常见题目, 要正确得出选择,需要有较好的作图能力和对定理、 公理的准确掌握、深刻理解,同时要考虑到各种情况.典型例题八例8 设平面 平面,平面 平面,且、 分别与 相交于a 、b , a//b .求 证:平面 //平面 . 分析:要证明两平面平行,只要设法在平面 上找到两条相交直线,或作出相交直线,它们分别与平行(如图)•例7设直线I 、m ,平面F 列条件能得出〃的是( )•A •I,m ,且 I //, m//C . I ,m,且 1 // m分析: 选项A 是错误的,因为当 I //m时,B • I , m ,且 I // m D • I // , m// ,且 I // m与可能相交•选项 B 是错误的,理由同A .选项C 是正确的,因为|证明:在平面内作直线PQ 直线a,在平面内作直线MN 直线b ••••平面平面,••• PQ 平面,MN 平面,••• PQ//MN •又•/ a// p, PQ a Q , MN b N ,•平面//平面•说明:如果在、内分别作PQ , MN ,这样就走了弯路,还需证明PQ、MN在、内,如果直接在、内作a、b的垂线,就可推出PQ// MN •由面面垂直的性质推出“线面垂直”,进而推出“线线平行”、“线面平行”,最后得到“面面平行”,最后得到“面面平行” •其核心是要形成应用性质定理的意识,在立体几何证明中非常重要.典型例题九⑴求证:MN //⑵求MN的长.,取AD的中点P ,只要证明MN所在的平面PMN //此证明PM // , PN //即可.(2)要求MN之长,在CMA中,CM、CN的长度易知,关键在于证明MN CD,从而由勾股定理可以求解.证明:(1)连结AD,设P是AD的中点,分别连结PM、PN • •/ M 是AB 的中点,• PM //BD •PM //例9如图所示,平面//平面,点A、C,点B、D ,AB a 是的公垂线,CD是斜线•若AC BD b, CD c, M、N分别是AB和CD的中点, 分析:(1)要证MN //又BD同理••• N是CD的中点,••• PN//AC ••/ AC ,• PN // ••/// , PN PM P,•平面PMN //••• MN 平面PMN , • MN //(2)分别连结MC、MD •1••• AC BD b, AM BM a , 2又••• AB是、的公垂线,• CAMDBM 90 ,• Rt ACM 也Rt BDM , • CM DM ,•- DMC是等腰三角形.又N是CD的中点,• MN CD •____________ 1 _______________在Rt CMN 中,MN CM2CN24b2a2c2•2说明:(1)证“线面平行”也可以先证“面面平行”,然后利用面面平行的性质,推证“线面平行”,这是一种以退为进的解题策略.(2)空间线段的长度,一般通过构造三角形、然后利用余弦定理或勾股定理来求解.⑶面面平行的性质:①面面平行,则线面平行;②面面平行,则被第三个平面所截得的交线平行.线线平行胡』线面平行面面平行典型例题十例10如果平面内的两条相交直线与平面所成的角相等,那么这两个平面的位置关系是___________ •分析:按直线和平面的三种位置关系分类予以研究. 解:设a、b是平面内两条相交直线.(1)若a、b都在平面内,a、b与平面所成的角都为0,这时与重合,根据教材中规定,此种情况不予考虑.⑵若a、b都与平面相交成等角,且所成角在(0 ,90)内;••• a、b与有公共点,这时与相交.若a、b都与平面成90角,贝U a//b,与已知矛盾.此种情况不可能.(3)若a、b都与平面平行,则a、b与平面所成的角都为0 , 内有两条直线与平面平行,这时〃综上,平面、的位置关系是相交或平行.典型例题十一例11 试证经过平面外一点有且只有一个平面和已知平面平行.已知:A 平面,求证:过A有且只有一个平面/ .分析:“有且只有”要准确理解,要先证这样的平面是存在的,再证它是惟一的,缺一不可.证明:在平面内任作两条相交直线a和b,则由A 知,A a, A b.点A和直线a可确定一个平面M,点A和直线b可确定一个平面N .在平面M、N内过A分别作直线a'// a、b'//b ,故a '、b'是两条相交直线,可确定一个平面.T a , a , a //a,二a //同理b ' // .又a , b , a b A,二// .所以过点A有一个平面// .假设过A点还有一个平面// ,则在平面内取一直线c , A c,点A、直线c确定一个平面,由公理2知:m ,n,••• m//c, n//c ,又A m,A n,这与过一点有且只有一条直线与已知直线平行相矛盾,因此假设不成立,所以平面只有一个.所以过平面外一点有且只有一个平面与已知平面平行.典型例题十二例12已知点S是正三角形ABC所在平面外的一点,且SA SB SC, SG为SAB 上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF内的位置关系,并给予证明分析1:如图,观察图形,即可判定SG//平面DEF,要证明结论成立,只需证明SG 与平面DEF内的一条直线平行.观察图形可以看出:连结CG与DE相交于H ,连结FH , FH就是适合题意的直线. 怎样证明SG// FH ?只需证明H是CG的中点.证法1:连结CG交DE于点H ,•/ DE是ABC的中位线,••• DE//AB .在ACG中,D是AC的中点,且DH // AG ,•H为CG的中点.•/ FH 是SCG的中位线,• FH //SG .又SG 平面DEF , FH 平面DEF ,•SG// 平面DEF .分析2:要证明SG//平面DEF,只需证明平面SAB //平面DEF,要证明平面DEF //平面SAB,只需证明SA//DF , SB// EF而SA// DF , SB// EF可由题设直接推出.证法2:•/ EF为SBC的中位线,•EF //SB.••• EF 平面SAB, SB 平面SAB,•EF // 平面SAB.同理:DF //平面SAB, EF DF F ,•平面SAB//平面DEF,又••• SG 平面SAB,•SG//平面DEF .典型例题十三例13如图,线段PQ分别交两个平行平面、于A、B两点,线段PD分别交、于C、D两点,线段QF分别交、于F、E两点,若PA 9, AB 12 , BQ 12 ,ACF的面积为72,求BDE的面积.分析:求BDE的面积,看起来似乎与本节内容无关,事实上,已知ACF的面积,若BDE与ACF的对应边有联系的话,可以利用ACF的面积求出BDE的面积.解: •••平面QAF AF,平面QAF BE ,又•••// ,二AF // BE •同理可证:AC//BD ,••• FAC与EBD相等或互补,即sin FAC sin EBD .由FA//BE,得BE : AF QB : QA 12: 24 1:2 ,1•BE - AF2由BD // AC,得:AC: BD PA: PB 9: 21 3: 7 ,• BD -AC .31又••• ACF 的面积为72,即一AF AC sin FAC 72 .21…S DBE BE BD sin EBD21 1 7AF — AC sin FAC2 2 37 1AF AC sin FAC6 2-72 84.6•BDE的面积为84平方单位.说明:应用两个平行的性质一是可以证明直线与直线的平行,二是可以解决线面平行的问题.注意使用性质定理证明线线平行时,一定第三个平面与两个平行平面相交,其交线互相平行.典型例题十四例14在棱长为a的正方体中,求异面直线BD和B1C之间的距离.分析:通过前面的学习,我们解决了如下的问题:若a和b是两条异面直线,则过a且平行于b的平面必平行于过b且平行于a的平面.我们知道,空间两条异面直线,总分别存在于两个平行平面内.因此,求两条异面直线的距离,有时可以通过求这两个平行平面之间的距离来解决.具体解法可按如下几步来求:①分别经过BD和B1C找到两个互相平等的平面;②作出两个平行平面的公垂线;③计算公垂线夹在两个平等平面间的长度. 解:如图,根据正方体的性质,易证:连结AC1,分别交平面ABD和平面CB1D1于M和N因为CC1和AC1分别是平面ABCD的垂线和斜线,AC在平面ABCD内,AC BD由三垂线定理:AC1 BD,同理:AC1 A.D--AC i 平面A i BD,冋理可证:AC i 平面CB1D1•••平面A,BD和平面CB1D1间的距离为线段MN长度.如图所示:在对角面AC i中,O i为AQ i的中点,0为AC的中点•AM MN NC i -AC i3 a3 3- V3 •BD和B i C的距离等于两平行平面A i BD和CB i D i的距离为 a .3说明:关于异面直线之间的距离的计算,有两种基本的转移方法:①转化为线面距.设a、b是两条异面直线,作出经过b而和a平行的平面,通过计算a和的距离,得出a 和b距离,这样又回到点面距离的计算;②转化为面面距,设a、b是两条异面直线,作出经过b而和a平行的平面,再作出经过a和b平行的平面,通过计算离得出a和b之间的距离.BD//BQAB//DQ平面A,BD〃平面CB1D1之间的距典型例题十五例15正方体ABCD ABCQ !棱长为a ,求异面直线 AC 与BG 的距离. 解法1:(直接法)如图:小结:这种解法是将线线距离转化为线面距离.取BC 的中点P ,连结PD 、PB_!分别交AC 、BC 1于M 、N 两点, 易证:DB 1 // MN , DB 1 AC , DB 1 BG .1 / 3 ••• MN 为异面直线 AC 与BC 1的公垂线段,易证: MNDB 1 a .33 小结:此法也称定义法, 这种解法是作出异面直线的公垂线段来解. 但通常寻找公垂线段时,难度较大.解法2:(转化法)如图:••• AC//平面 AGB ,•- AC 与BC 1的距离等于 AC 与平面AG B 的距离, 在Rt OBO 1中,作斜边上的高0E ,贝U OE 长为所求距离,•/ OB △ , OO 1• O 1BOQ OB O 1B.3 a .3AtB LA 4解法3:(转化法)如图:•••平面 ACD i //平面 AiGB ,二AC 与BC 1的距离等于平面 ACD 1与平面A 1C 1B 的距离. -DB i 平面ACD i ,且被平面 ACD i 和平面A 1C 1B 二等分;1•••所求距离为-B 1D3小结:这种解法是线线距离转化为面面距离. 解法4:(构造函数法)如图:任取点Q BC 1 ,作QRBC 于R 点,作 P K AC 于K 点,设RC x ,则 BR QR a x , CKKR ,且 KR 2 CK 2 CR 2• KR 2^CR 21 2 x .2 2则QK 2 1 2 x(a x)2故QK 的最小值,即AC 与BC i 的距离等于小结:这种解法是恰当的选择未知量, 构造一个目标函数, 通过求这个函数的最小值来得到二异面直线之间的距离.解法5:(体积桥法)如图:3(x 2 a ) 2 31 239,DAB 2,直线AB 与平面解法1:如图所示:所成的角为30,求线段AC 长的取值范围.当求AC 与BC 1的距离转化为求 AC 与平面AC j B 的距离后,设C 点到平面A 1C 1B 的 距离为h ,••• h —2 a •即AC 与BCi 的距离等于 —a •3 3小结:本解法是将线线距离转化为线面距离,再将线面距离转化为锥体化为锥体的高, 然后用体积公式求之•这种方法在后面将要学到.说明:求异面直线距离的方法有:(1) (直接法)当公垂线段能直接作出时,直接求•此时,作出并证明异面直线的公垂 线段,是求异面直线距离的关键.(2)(转化法)把线线距离转化为线面距离,如求异面直线a 、b 距离,先作出过a 且平行于b 的平面 ,则b 与 距离就是a 、b 距离.(线面转化法)•也可以转化为过a 平行b 的平面和过b 平行于a 的平面,两平行平面的距离就是两条异 面直线距离.(面面转化法).(3) (体积桥法)利用线面距再转化为锥体的高用何种公式来求.(4) (构造函数法)常常利用距离最短原理构造二次函数,利用求二次函数最值来解. 两条异面直线间距离问题,教科书要求不高(要求会计算已给出公垂线时的距离) ,这方面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.典型例题十六例16如果 // , AB 和AC 是夹在平面 与 之间的两条线段, AB AC ,且则 V c A1C 1BV A i BCC 1•3• AC 必在过点 A 且与直线 AB 垂直的平面 内设丨,则在 内,当AC l 时,AC 的长最短,且此时 AC AB tan ABCAB tan 30而在 内,C 点在丨上移动,远离垂足时,AC 的长将变大,从而AC :3即AC 长的取值范围是••• AB BD , AC DC , AB 2 AC 2 BC 2, •••在BDC 中,由余弦定理,得:cos BDCBD 2 CD 2 BC 2 AB 2 AC 2 BC 22BD CD2BD CD•/ AD• ABD 是AB 与所在的角.又•••// ,作AD于 D ,连结 BD 、CD 、BC.ABDABD 也就等于AB 与 所成的角,即 2, •/ AB ••• AD 1,BD 3,DC .. AC 2BC..4 AC 2, • AC解法2: •/ AB 2 23 AC 14 AC o ,即:2 “3 .AC 2 12 3T ,即AC 长的取值范围为如图:AC说明:(1)本题考查直线和直线、直线和平面、平面和平面的位置关系,对于运算能力和空间想象能力有较高的要求,供学有余力的同学学习.(2)解法1利用余弦定理,采用放缩的方法构造出关于AC长的不等式,再通过解不等式得到AC长的范围,此方法以运算为主.⑶解法2从几何性质角度加以解释说明,避免了繁杂的运算推导,但对空间想象能力要求很高,根据此解法可知线段AC是连结异面直线AB和I上两点间的线段,所以AC是AB与I的公垂线段时,其长最短.典型例题十七例17如果两个平面分别平行于第三个平面,那么这两个平面互相平行.已知:// , // ,求证:// •分析:本题考查面面平行的判定和性质定理以及逻辑推理能力. 由于两个平面没有公共点称两平面平行,带有否定性结论的命题常用反证法来证明,因此本题可用反证法证明. 另外也可以利用平行平面的性质定理分别在三个平面内构造平行且相交的两条直线,利用线线平行来推理证明面面平行,或者也可以证明这两个平面同时垂直于某一直线.证明一:如图,假设、不平行,则和相交.•••和至少有一个公共点A,即A , A .•- // , // ,•A .于是,过平面外一点A有两个平面、都和平面平行,这和“经过平面外一点有且只有一个平面与已知平面平行”相矛盾,假设不成立。