2019届中考数学总复习 第四章 图形的初步认识与三角形 方法技巧(一)几何中与角平分线有关的计算与

方法技巧训练(一) 与角平分线有关的基本模型方法指导1三角形中角平分线的夹角的计算 类型1 两个内角平分线的夹角如图1，在△ABC 中，∠ABC ，∠ACB 的平分线BE ，CF 相交于点G ，则∠BGC ＝90°＋12∠A.图1 图2图3解题通法：三角形两内角的平分线的夹角等于90°与第三个内角的一半的和． 类型2 一个内角平分线和一个外角平分线的夹角如图2，在△ABC 中，BP 平分∠ABC ，CP 平分∠ACB 的外角，BP 与CP 相交于点P ，则∠P ＝12∠A.解题通法：三角形一内角与另一外角的平分线的夹角等于第三个内角的一半． 类型3 两外角平分线的夹角如图3，在△ABC 中，BO ，CO 是△ABC 的外角平分线，则∠O ＝90°－12∠A.解题通法：三角形两外角的平分线的夹角等于90°与第三个内角的一半的差．Ｋ1．如图，在△ABC 中，∠A ＝40°，点D 是∠ABC 和∠ACB 的平分线的交点，则∠BDC ＝110°．【变式1】如图，若点D 是∠ABC 的平分线与∠ACB 外角平分线的交点，则∠D ＝20°．【变式2】如图，若点D 是∠ABC 外角平分线与∠ACB 外角平分线的交点，则∠D ＝70°．【变式3】如图，BA 1和CA 1分别是△ABC 的内角平分线和外角平分线，BA 2是∠A 1BD 的平分线，CA 2是∠A 1CD 的平分线，BA 3是∠A 2BD 的平分线，CA 3是∠A 2CD 的平分线．若∠A 1＝α，则∠A 2 019＝α22 018．方法指导2与角平分线有关的图形与辅助线1．角平分线＋平行线→等腰三角形如图4，BD是∠ABC的平分线，点O是BD上一点，OE∥BC交AB于点E，则△BOE是等腰三角形．解题通法：遇到角平分线及平行线，除了可以得到角度的关系，还可以得到一个等腰三角形．图4 图5 图6 图72．与角平分线有关的辅助线①过角平分线上的点作角两边的垂线如图5，BO是∠ABC的平分线，过点O作OE⊥AB于点E，过点O作OF⊥BC于点F，则OE＝OF，△BEO≌△BFO.②角平分线的两端过角的顶点取相等的两条线段构造全等三角形如图6，BO是∠ABC的平分线，在BA，BC上取线段BE＝BF，则△BEO≌△BFO.解题通法：遇到角平分线时，我们通常过角平分线上的一点向两边作垂线或在角平分线的两端取相等的线段构造全等三角形．③过角平分线上一点作角平分线的垂线，从而得到等腰三角形．如图7，BD是∠ABC的平分线，点E是BD上一点，过点E作BD的垂线，则△BGH是等腰三角形且BD垂直平分GH.2.如图，在△ABC中，AB＝10 cm，AC＝8 cm，∠ABC和∠ACB的平分线交于点O，过点O作BC的平行线MN交AB于点M，交AC于点N，则△AMN的周长为(D)A．10 cm B．28 cm C．20 cm D．18 cm3.如图，矩形ABCD中，AB＝4 cm，BC＝8 cm，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积(B)A．8 cm2B．10 cm2C．15 cm2D．20 cm24．(2018·大庆)如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC，且∠ADC＝110°，则∠MAB＝(B) A．30°B．35°C．45°D．60°5．如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB＝10，BC＝15，MN＝3，则AC的长是16．提示：延长BN交AC于点E.因为AN平分∠BAC，BN⊥AN，可证△ABN≌△AEN，则AN是△ABE的中线，即点N 平分BE，所以MN是△BEC的中位线．6．如图，在△ABC中，∠A＝60°，BD，CE分别平分∠ABC和∠ACB，BD，CE相交于点O，试说明BE，CD，BC的数量关系，并加以说明．解：BC ＝BE ＋CD.理由如下：在BC 上取点G ，使得CG ＝CD ，连接OG.∵∠BOC ＝180°－12(∠ABC ＋∠ACB)＝180°－12×(180°－60°)＝120°，∴∠BOE ＝∠COD ＝60°.∵BD ，CE 分别平分∠ABC 和∠ACB ， ∴∠EBO ＝∠GBO ，∠OCG ＝∠OCD. 在△COD 和△COG 中，⎩⎪⎨⎪⎧CO ＝CO ，∠DCO ＝∠GCO ，CD ＝CG ，∴△COD ≌△COG(SAS)．∴∠COG ＝∠COD ＝60°.∴∠BOG ＝120°－60°＝60°＝∠BOE. 在△BOE 和△BOG 中，⎩⎪⎨⎪⎧∠BOE ＝∠BOG ，BO ＝BO ，∠EBO ＝∠GBO ，∴△BOE ≌△BOG(ASA)．∴BE ＝BG.∴BE ＋CD ＝BG ＋CG ＝BC.7．感知：如图1，AD 平分∠BAC.∠B ＋∠C ＝180°，∠B ＝90°，易知：DB ＝DC.探究：如图2，AD 平分∠BAC ，∠ABD ＋∠ACD ＝180°，∠ABD ＜90°，求证：DB ＝DC.应用：如图3，在四边形ABCD 中，∠B ＝45°，∠C ＝135°，DB ＝DC ＝a ，则AB －AC 用含a 的代数式表示)．图1 图2图3证明：过点D 作DE ⊥AB 于点E ，DF ⊥AC 交AC 的延长线于点F. ∵AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF.∵∠B ＋∠ACD ＝180°，∠ACD ＋∠FCD ＝180°，∴∠B ＝∠FCD. 在△DFC 和△DEB 中，⎩⎪⎨⎪⎧∠F ＝∠DEB ，∠FCD ＝∠B ，DF ＝DE ，∴△DFC ≌△DEB(AAS)．∴DC ＝DB.。

第二节三角形的根本概念及全等三角形,怀化七年中考命题规律)年份题型题号考察点考察内容分值总分2021解答17全等三角形全等三角形的判定及其性质882021 解答17三角形中位线利用三角形的中位线的性质得条件，证三角形全等882021选择5全等三角形以等腰梯形为背景，判断三角形全等3填空15三角形内外角关系利用三角形的内外角关系求角362021选择5三角形中位线以测量池塘为背景，利用三角形中位线的性质得33到两点间的距离2021解答19全等三角形以等腰梯形为背景证三角形全等10填空11三角形中位线以平行四边形为背景，利用三角形中位线的性质求线段的长度3132021选择2三角形内外角的关系利用三角形的外角及内角的关系比拟大小33命题规律纵观怀化七年中考，“三角形的根本概念及全等三角形〞这一考点其余各年都有考察，根本概念考察层次偏低，全等三角形考察中等，其中，三角形内外角关系考察2次，三角形中位线考察3次，全等三角形考察3次．命题预测预计2021年怀化中考会以三角形中的重要线段，三主要考察对象，全等三角形的判定与性质也会在解答题中考察.,怀化七年中考真题及模拟)三角形的内外角关系(2次)1．(2021怀化中考)如下图，∠A，∠1，∠2的大小关系是( B)A．∠A>∠1>∠2 B．∠2>∠1>∠AC．∠A>∠2>∠1 D．∠2>∠A>∠1(第1题图)(第2题图)2．(2021怀化中考)如图，在△ABC中，∠A＝30°，∠B＝50°，延长BC 到D，那么∠ACD＝__80°__．三角形的中位线(3次)3．(2021怀化中考)如图，为测量池塘边A，B两点的距离，小明在池塘的一侧选取一点O，测得OA，OB的中点分别是点D，E，且DE＝14 m，那么A，B间的距离是( C)A．18 m B．24 m C．28 m D．30 m(第3题图)(第4题图)4．(2021怀化中考)如图，在▱ABCD中，AD＝8，点E，F分别是BD，CD 的中点，那么EF＝__4__．全等三角形(3次)5．(2021怀化中考)如图，等腰梯形ABCD中，AD∥BC，AB＝DC，AC及BD相交于点O，那么以下判断不正确的选项是( B)A．△ABC≌△DCB B．△AOD≌△COBC ．△ABO ≌△DCOD ．△ADB ≌△DAC(第5题图)(第6题图)6．(2021怀化二模)如图，OP 是∠AOB 的平分线，点C ，D 分别在角的两边OA ，OB 上．添加以下条件，不能判定△POC≌△POD 的选项是( D )A ．PC ⊥OA ，PD ⊥OB B ．OC ＝OD C ．∠OPC ＝∠OPD D ．PC ＝PD7．(2021怀化学业考试指导)一个等腰三角形的两边长分别为2与5，那么它的周长为( C )A ．7B ．9C ．12D ．9或128．(2021鹤城模拟)三角形的两边长分别为3与6，第三边的长是方程x 2－6x ＋8＝0的一个根，那么这个三角形的周长是( D )A ．2或4B ．11或13C ．11D ．139．(2021芷江模拟)在△ABC 中，∠ABC ＝30°，AB 边长为10，AC 边的长度可以在3、5、7、9、11中取值，满足这些条件的互不全等的三角形的个数是( D )A ．3个B ．4个C ．5个D ．6个10．(2021怀化考试说明)如图，D 为△ABC 内一点，CD 平分∠ACB，BE ⊥CD ，垂足为D ，交AC 于点E ，∠A ＝∠ABE，假设AC ＝5，BC ＝3，那么BD 的长为( D )A ．2.5B ．1.5C ．2D ．111．(2021怀化中考)如图，在等腰梯形ABCD 中，点E 为底边BC 的中点，连接AE ，DE.求证：AE ＝DE.证明：∵四边形ABCD 为等腰梯形，∴AB ＝DC ，∠B ＝∠C，∵E 为BC 的中点，∴BE ＝CE ，∴△ABE ≌△DCE(SAS )，∴AE ＝DE.12．(2021怀化中考)如图，AD ＝BC ，AC ＝BD. (1)求证：△ADB≌△BCA；(2)OA 及OB 相等吗？假设相等，请说明理由．证明：(1)在△ADB 与△BCA 中，⎩⎪⎨⎪⎧AD ＝BC ，AC ＝BD ，AB ＝BA ，∴△ADB ≌△BCA(SSS )；(2)OA ＝OB.理由如下：∵△ADB≌△BCA，∴∠DBA ＝∠CAB，即∠OAB＝∠OBA，∴OA ＝OB.13．(2021怀化一模)如图，点E ，F 在BC 上，BE ＝CF ，∠A ＝∠D，∠B ＝∠C，求证：AB ＝DC.证明：∵BE＝CF ，∴BF ＝CE ，又∵∠A＝∠D，∠B ＝∠C，∴△ABF ≌△DCE ，∴AB ＝DC.14．(2021洪江模拟)△ABN 与△ACM 的位置如下图，AB ＝AC ，AD ＝AE ，∠1＝∠2.求证：(1)BD ＝CE ；(2)∠M＝∠N.证明：(1)∵在△ABD 与△ACE中，⎩⎪⎨⎪⎧AB ＝AC ，∠1＝∠2，AD ＝AE ，∴△ABD ≌△ACE ，∴BD ＝CE ；(2)∵△ABD≌△ACE，∴∠ADB ＝∠AEC.又∵∠MDO＝∠ADB，∠NEO ＝∠AEC，∴∠MDO ＝∠NEO.∵∠MOD＝∠NOE，∴180°－∠MDO－∠MOD＝180°－∠NEO－∠NOE，∴∠M ＝∠N.考点清单)三角形分类及三边关系1．三角形分类 (1)按角分类锐角三角形直角三角形钝角三角形(2)按边分类两条边相等的三角形 三边相等的三角形 三边互不相等的三角形 __等腰__三角形__等边__三角形不等边三角形2．三边关系：三角形任意两边之与__大于__第三边，任意两边之差小于第三边，如图，__a ＋b__>c ，|a －b|<__c__．3．判断几条线段能否构成三角形：运用三角形三边关系判定三条线段能否构成三角形，并不一定要列出三个不等式，只要两条较短的线段长度之与大于第三条线段的长度即可判断这三条线段能构成一个三角形．三角形内角与定理及内外角关系4．内角与定理：三角形的内角与等于__180°__．5．内外角关系：三角形的一个外角__等于__及它不相邻的两个内角之与．三角形的一个外角大于任何一个与它不相邻的内角．三角形中的四条重要线段四线定义性质 图形中线连接一个顶点及它对边中点的线段BD ＝DC高线从三角形一个顶点到它对边所在直线的垂线段AD⊥BC，即∠ADB＝∠ADC＝90°续表角平分线一个内角的平分线及这个角的对边相交，顶点及交点之间的线段∠1＝∠2中位线连接三角形两边中点的线段DE∥BC且DE＝12BC全等三角形及其性质6．定义：能完全重合的两个三角形叫做全等三角形．7．性质：(1)全等三角形的对应边__相等__，对应角__相等__．(2)全等三角形的对应线段(角平分线、中线、高线、中位线)相等，对应__周长__相等，对应面积__相等__．全等三角形的判定8．三角形全等的判定类型图形条件是否全等形成结论一般三角形的判定A1B1＝A2B2，B1C1＝B2C2，A1C1＝A2C2是__SSS__∠B1＝∠B2，B1C1＝B2C2，∠C1＝∠C2是ASA ∠B1＝是AAS∠B 2， ∠C 1＝∠C 2， A 1C 1＝A 2C 2 A 1B 1＝A 2B 2， ∠B 1＝∠B 2， B 1C 1＝B 2C 2 是 __SAS __续表直角 三角 形的 判定A 1B 1＝A 2B 2，A 1C 1＝A 2C 2，是__HL __【方法技巧】证明三角形全等的思路判定三角形全等⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧两边⎩⎪⎨⎪⎧找夹角→SAS 找直角→HL 或SAS找另一边→SSS 一边和一角⎩⎪⎨⎪⎧边为角的对边→找任一角→AAS 边为角的邻边⎩⎪⎨⎪⎧找夹角的另一边→SAS 找夹边的另一角→ASA 找边的对角→AAS两角⎩⎪⎨⎪⎧找夹边→ASA找任一边→AAS,中考重难点突破)三角形三边关系【例1】(2021 洪江模拟)如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2、3、4、6，且相邻两木条的夹角均可调整．假设调整木条的夹角时不破坏此木框，那么任意两个螺丝间距离的最大值为( )A ．5B ．6C ．7D ．10【解析】4条木棍的四边长为2、3、4、6；①选2＋3、4、6作为三角形，那么三边长为5、4、6；5－4<6<5＋4，能构成三角形，此时两个螺丝间的最大距离为6；②选3＋4、6、2作为三角形，那么三边长为2、7、6；6－2<7<6＋2，能构成三角形，此时两个螺丝间的最大距离为7；③选4＋6、2、3作为三角形，那么三边长为10、2、3；2＋3<10，不能构成三角形，此种情况不成立；④选6＋2、3、4作为三角形，那么三边长为8、3、4；而3＋4<8，不能构成三角形，此种情况不成立．综上所述，任意两个螺丝间距离的最大值为7. 【学生解答】C1．(2021岳阳中考)以下长度的三根小木棒能构成三角形的是( D ) A ．2 cm ，3 cm ，5 cm B ．7 cm ，4 cm ，2 cm C ．3 cm ，4 cm ，8 cm D ．3 cm ，3 cm ，4 cm三角形的内角与外角关系【例2】(2021原创)如图，CD 是△ABC 外角∠ACE 的平分线，AB ∥CD ，∠A ＝50°，那么∠B 的大小是( )A ．50°B ．60°C ．40°D ．30°【解析】∵AB∥CD，∴∠A ＝∠ACD＝50°，又∵CD 是△ABC 外角∠ACE 的平分线，∴∠ACD ＝∠DCE＝50°，∴∠ACE ＝2∠ACD＝100°，由三角形内外角关系可得∠B ＋∠A＝∠ACE，∴∠B ＝∠ACE －∠A ＝100°－50°＝50°.【学生解答】A2．(2021乐山中考)如图，CE 是△ABC 的外角∠ACD 的平分线，假设∠B＝35°，∠ACE ＝60°，那么∠A＝( C )A ．35°B ．95°C ．85°D ．75°三角形中重要线段的应用【例3】在△ABC 中，D 为AB 的中点，E 为AC 上一点，CE ＝13AC ，BE ，CD 交于点O ，BE ＝5 cm ，那么OE ＝________cm .(例3题图)(例3题解图)【解析】如解图，过D 作DF∥BE，那么DF 就是三角形ABE 的中位线，∴DF ＝12BE ，AF ＝EF ，又∵CE ＝13AC ，∴CE ＝EF ，∴OE 就是三角形CDF 的中位线，∴OE ＝12DF ＝14BE ＝1.25 cm .【学生解答】1.253．(2021枣庄中考)如图，△ABC 的面积为6，AC ＝3，现将△ABC 沿AB 所在直线翻折，使点C 落在直线AD 上的C′处，P 为直线AD 上的一点，那么线段BP 的长不可能是( A )A ．3B ．4C ．5.5D ．10全等三角形的证明及性质【例4】如图，点D 为等腰Rt △ABC 内一点，∠CAD ＝∠CBD＝15°，E 为AD 延长线上的一点，，且DC ＝DM ，试探究线段ME 及BD 的数量关系，并说明理由．【解析】连接MC ，先证△BDC≌△ADC，再证△ADC≌△EMC.【学生解答】解：如图，连接MC ，在等腰Rt △ABC 中，∵∠CAD ＝∠CBD＝15°，∴∠BAD ＝∠ABD＝45°－15°＝30°，∴BD ＝AD ，又AC ＝BC ，∴△BDC ≌△ADC(SSS )，∴∠DCA ＝∠DCB＝45°，∠EDC ＝∠DAC＋∠DCA＝15°＋45°＝60°.∵DC ＝DM ，∴△MDC 是等边三角形，即CM ＝CD ，又∵∠EMC＝180°－∠DMC＝180°－60°＝120°，∠ADC ＝180°－∠MDC ＝180°－60°＝120°，∴∠EMC ＝∠ADC.又∵CE＝CA ，∴∠DAC ＝∠CEM ＝15°，∴△ADC ≌△EMC(AAS )，∴ME ＝AD ＝DB ，∴ME ＝BD.4．(2021南京中考)如图，四边形ABCD 的对角线AC 、BD 相交于点O ，△ABO ≌△ADO ，以下结论：①AC⊥BD；②CB＝CD ；③△ABC≌△ADC；④DA ＝DC ，其中正确结论的序号是__①②③__．图形旋转中全等三角形的判定及性质【例5】(2021 苏州中考)如图，在Rt △ABC 中，∠ACB ＝90°，点D ，F 分别在AB ，AC 上，CF ＝CB ，连接CD ，将线段CD 绕点C 按顺时针方向旋转90°后得CE ，连接EF.(1)求证：△BCD≌△FCE；(2)假设EF∥CD，求∠BDC 的度数．【解析】(1)由旋转的性质可得：CD ＝CE ，再根据同角的余角相等可证明∠BCD＝∠FCE，再根据全等三角形的判定方法即可证明△BCD≌△FCE.(2)由(1)可知△BCD≌△FCE，所以∠BDC＝∠E，易求∠E＝90°，进而可求出∠BDC 的度数．【学生解答】解：(1)∵将线段CD 绕点C 按顺时针方向旋转90°后得CE ，∴CD ＝CE ，∠DCE ＝90°，又∵∠ACB ＝90°，∴∠BCD ＝90°－∠ACD＝∠FCE，在△BCD 与△FCE中，⎩⎪⎨⎪⎧CB ＝CF ，∠BCD ＝∠FCE，CD ＝CE ，∴△BCD ≌△FCE(SAS )；(2)第 11 页 由(1)可知△BCD≌△FCE ，∴∠BDC ＝∠E ，∵EF ∥CD ，∴∠E ＝180°－∠DCE＝90°，∴∠BDC ＝90°.5．(2021怀化三模)如图，在Rt △ABC 中，∠ABC ＝90°，点D 在边AB 上，使DB ＝BC ，过点D 作EF⊥AC，分别交AC 于点E ，交CB 的延长线于点F.求证：AB ＝BF.提示：证Rt △ABC ≌Rt △FBD 即可．6．(2021淄博中考)如图，△ABC，AD 平分∠BAC 交BC 于点D ，BC 的中点为M ，ME ∥AD ，交BA 的延长线于点E ，交AC 于点F.求证：(1)AE ＝AF ；(2)BE ＝12(AB ＋AC)． 证明：(1)∵AD 平分∠BAC，∴∠BAD ＝∠CAD.∵AD∥EM，∴∠BAD ＝∠AEF ，∠CAD ＝∠AFE ，∴∠AEF ＝∠AFE ，∴AE ＝AF ；(2)过点C 作CG∥EM，交BA 的延长线于点G ，∴∠AGC ＝∠AEF，∠ACG ＝∠AFE.∵∠AEF ＝∠AFE，∴∠AGC ＝∠ACG，∴AG ＝AC.∵BM＝CM ，EM ∥CG ，∴BE ＝EG ，∴BE ＝12BG ＝12(BA ＋AG)＝12(AB ＋AC)．。

第四章图形的认识与三角形第十五讲图形初步及相交线、平行线【基础知识回顾】一、直线、射线、线段线段公理：直线公理：【名师提醒：一条直线上有n个点，则这条直线上存在条线段】二、角1、定义：有公共端点的两条组成的图形叫做角，角也可以看做是一条绕它的从一个位置旋转到另一个位置所形成的图形【名师提醒：角的表示方法：可以用三个大写字母表示，如：∠AOB，也可用一个大写字母，如∠A表示，或用一个数字或希腊字母表示，如∠1、∠α等，注意善于选择合适、简洁的方法表示角】2、角的分类：角按照大小可分为：周角、、锐角等。

其中1周角= 度= 平角直角1度= 分1分= 秒【名师提醒：钟表转动过程中常见时针，分针的夹角问题，要牢记一个前提：即时针每分转动度，分针每分转动度】3、角的平分线一条射线把一个角分成的角，这条叫做这个角的平分线【名师提醒：有公共顶点的n条射线，一共可形成个小于平角的角】1、互为余角互为补角①互为余角：若∠1+∠2=则称∠1与∠2互为余角②互为补角：若∠1+∠2=则称∠1与∠2互为补角3性质：同角或等角的余角，同角或等角的补角【名师提醒：1、互补和互余是指两个角的关系2、一个锐角的补角比它的余角大度】三、相交线1、对顶角及其性质：对顶角和邻补角：两条直线相交所成的四个角中如图：对顶角有邻补角有对顶角性质：2、垂线及其性质互相垂直：两条直线相交所构成的四个角中有一个角是，则这两条直线互相垂直，其中一条直线叫另一条直线的。

性质：1、过一点与已知直线垂直2、直线外一点与直线上各点连接的所有线段中，最短，（简称：）【名师提醒：注意三个距离的区别1、两点间的距离是指：2、点到直线的距离是指3、两平行线间的距离是指】四、平行线：1、三线八角：如图：两条直线AB与CD被第三条直线EF所截，构成八个角其中同位角有 对，分别是 ，内错角有 对，分别是 同旁内角有 对，分别是2、平行线的定义：在同一平面内 的两条直线叫平行线3、平行公理：经过已知直线外一点 条直线与已知直线平行4、平行线的性质和判定两直线平行 ————→【名师提醒：平行线的常用判定方法还有两条：1、平行于同一直线的两条直线互相 2、 同一直线的两条直线互相平行】 五、 命题、公理、定理和证明1、命题： 的语句叫命题，一个命题由 和 两部分构成，可分为 和 两类【名师提醒：1、判断一个命题是真命题要能给出 判断一个命题是假命题可以举出2、任何一个命题一定有它的逆命题：对于任意一个定理 有它的逆定理】 【重点考点例析】1.如果一个角的补角是150○，那么这个角的余角是____________2.如图，直线AB 、CD 相交于点O ，若∠BOD=40°，OA 平分∠COE ，则∠AOE= ．3.下列命题是真命题的有（ ）①对顶角相等；②两直线平行，内错角相等；③两个锐角对应相等的两个直角三角形全等； ④有三个角是直角的四边形是矩形；⑤平分弦的直径垂直于弦，并且平分弦所对的弧． A ．1个 B ．2个 C ．3个 D ．4个 4.如图，直线l 1∥l 2，若∠1=140°，∠2=70°，则∠3的度数是（ ） A ．70° B ．80° C ．65° D ．60° 5.把15°30′化成度的形式，则15°30′= 度．6.如图，一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上，若∠1=25°，则∠2= ．7.如图，直线l 1∥l 2∥l 3，点A 、B 、C 分别在直线l 1、l 2、l 3上．若∠1=70°，∠2=50°，相等 同旁内角 性质 判定相等则∠ABC= 度．8.如图，若∠1=40°，∠2=40°，∠3=116°30′，则∠4= ．9.如图，直线AD与AB、CD相交于 A、D两点，EC、BF与AB、CD交于点E、C、B、F，且∠l=∠2，∠B=∠C，求证：∠A=∠D．10.如图所示，在△ABC中，∠A＝50°，BO、CO分别平分∠ABC和∠ACB．求∠BOC的度数．11.已知：如图，CD⊥AB于D，E是BC上一点，EF⊥AB于F．∠l=∠2．求证：∠AGD=∠ACB．第十六讲三角形与全等三角形一：【知识梳理】1.三角形中的主要线段（1）三角形的角平分线：（2）三角形的中线：（3）三角形的高： (4) 三角形的中位线：2.三角形的边角关系（1）三角形边与边的关系：（2）三角形中角与角的关系：三角形三个内角之和等于180o．一个外角等于3.三角形的分类（1）按边分：⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形底和腰不等的等腰三角形等腰三角形等边三角形（2）按角分：⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形锐角三角形斜三角形钝角三角形4.中位线性质定理：三角形中位线：12 AD BD DE BC AE BEDE BC⎧==⎫⎪⇒⎬⎨=⎭⎪⎩∥5.全等三角形的性质：全等三角形的判定：【重点考点例析】1.如果一个三角形的两边长分别为2和4，则第三边长可能是（）A．2 B．4 C．6 D．82.如图：已知D、E分别在AB、AC上，AB=AC，∠B=∠C，求证：BE=CD．E DA3.如图，AF=DC，BC∥EF，只需补充一个条件，就得△ABC≌△DEF．4.如图，∠1=100°，∠C=70°，则∠A的大小是（）A．10°B．20°C．30°D．80°5.如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．6.如图，已知AB、CD相交于点O，AC∥BD，OC=OD，E、F为AB上两点，且AE=BF，试说明CE＝DF．第十七讲等腰三角形与直角三角形【基础知识回顾】一、等腰三角形1、等腰三角形的性质：⑴等腰三角形的两腰等腰三角形的两个底角简称为⑵等腰三角形的顶角平分线、互相重合，简称为⑶等腰三角形是轴对称图形，它有条对称轴，是2、等腰三角形的判定：⑴定义法：有两边相等的三角形是等腰三角形⑵有两相等的三角形是等腰三角形，简称【名师提醒：1、等腰三角形的性质还有：等腰三角形两腰上的相等，两腰上的相等，两底角的平分线也相等。

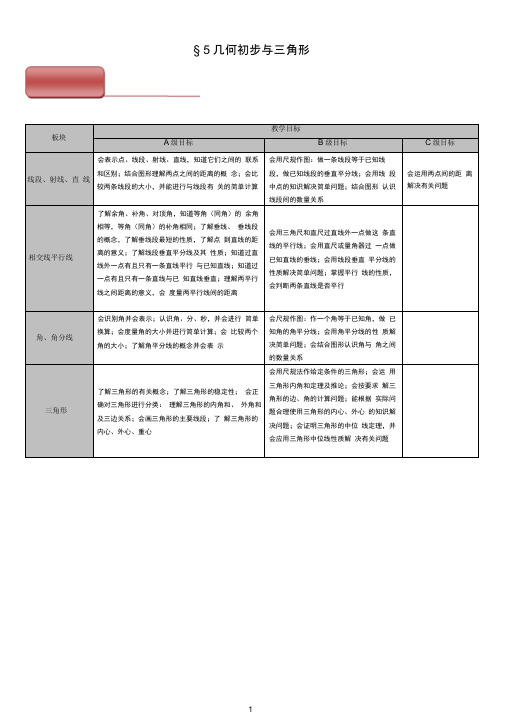
§ 5几何初步与三角形■7知识梳理、点、线、面和角 1、线段、射线、直线 直线、射线、线段的概念： ① 在直线的基础上定义射线、线段： 直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点. 直线上两点和中间的部分叫线段，这两个点叫线段的端点.② 在线段的基础上定义直线、射线： 把线段向一方无限延伸所形成的图形叫射线， 把线段向两方无限延伸所形成的图形是直线. 点与直线的关系： 点在直线上；点在直线外. 两个重要公理： ① 经过两点有且只有一条直线，也称为 两点确定一条直线”. ② 两点之间的连线中，线段最短，简称 两点之间，线段最短”. 两点之间的距离： 两点确定的线段的长度. ⑴点的表示方法： 我们经常用一个大写的英文字母表示点： A , B , C , D ,…… ⑵直线的表示方法： ①用两个大写字母来表示，这两个大写字母表示直线上的点，不分先后顺序，如直线 AB,如下图⑴也可以写作直线 BA . A BI• • --------------------------------------------------------------------------------------------------------------------------(1) ⑵②用一个小写字母来表示，如直线 I ，如上图⑵. 注意：在直线的表示前面必须加上 直线”二字；用两个大写字母表示时字母不分先后顺序. ⑶射线的表示方法： ① 用两个大写字母来表示. 第一个大写字母表示射线的端点,⑶，但不能写作射线 A0. ② 用一个小写字母来表示，如射线 I ，如图⑷. 第二个大写字母表示射线上的点. 如射线0A ,如图 O A I♦ . • ---------------------------------------------- 注意：在射线的表示前面必须加上 射线”二字.用两个大写字母表示射线时字母有先后顺序，射线的端点在前. ⑷线段的表示方法:① 用两个大写字母来表示，这两个大写字母表示线段的两个端点，无先后顺序之分，如线段 写作线段BA . ② 也可以用一个小写字母来表示：如线段 I ，如图⑹. AB ,如图⑸，也可以 A B• ------------------ ■ (5)I(6)注意：在线段的表示前面必须加上 线段”二字.用两个大写字母表示线段时字母不分先后顺序. 直线、射线、线段的主要区别：线段2个两者都有无顺序2、角板块一基本概念知识点角的定义定义1 ：有公共端点的两条射线组成的图形叫角，这个公共端点是角的顶点，这两条射线是角的两条边.角的大小只与开口的大小有关，而与角的边画出部分的长短无关•这是因为角的边是射线而不是线段定义2 :角由一条射线绕着它的端点旋转到另一个位置所成的图形，处于初始位置的那条射线叫做角的始边, 的那条射线叫做角的终边•(1) 如果角的终边是由角的始边旋转半周而得到，这样的角叫平角(2) 如果角的终边是由角的始边旋转一周而得到，这样的角叫周角注意：由角的定义可知：(1)角的组成部分为：两条边和一个顶点；(2)顶点是这两条边的交点；(3)角的两条边是射线，是无限延伸的(4)射线旋转时经过的平面部分称为角的内部，平面的其余部分称为角的外部知识点角的表示方法①利用三个大写字母来表示，如图 1.1.注意顶点一定要写在中间.也可记为.BOA，但不能写成.BAO或.ABO等.②利用一个大写字母来表示，如图 1.2.注意用一个大写字母来表示角的时候，这个大写字母一定要表示角的顶点，而且以它为顶点的角有且只有一个.③用数字来表示角，如图2.1 .④用希腊字母来表示角，如图2.2.知识点单位换算1 度=60 分⑴=60 ） 1 分=60 秒（1=60 ）终止位置./AOB图1.2板块二角度求解知识点角的度量(1)度量角的工具常用量角器用量角器注意：对中(顶点对中心)、重合(角的一边与量角器上的零刻度重合)、读数(读出角的另一边所在线的度数)(2)角的度量单位及其换算角的度量单位是度、分、秒.把平角分成180等份，每一份就是一度的角，记做 1 .把一度的角60等分，每一份叫做1分的角，记做1 •把一分的角60等分，每一份叫做1秒的角，记做1 .角度之间的关系1周角=360 1平角=180 1直角=901周角=2平角1平角=2直角角的分类：锐角a ( 0 £0( <90。