下载文档原格式
5.5 稳定裕度5.5.1 稳定裕度的定义控制系统稳定与否是绝对稳定性的概念。
而对一个稳定的系统而言，还有一个稳定的程度，即相对稳定性的概念。
相对稳定性与系统的动态性能指标有着密切的关系。
在设计一个控制系统时，不仅要求它必须是绝对稳定的，而且还应保证系统具有一定的稳定程度。
只有这样，才能不致因系统参数的小范围漂移而导致系统性能变差甚至不稳定。
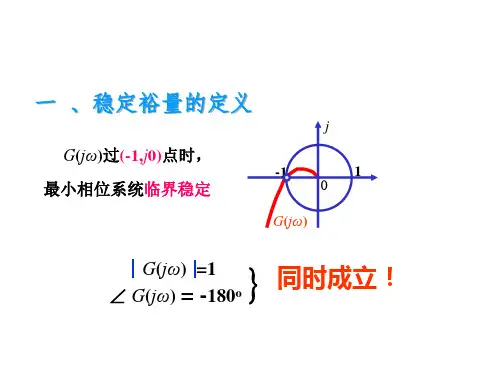
对于一个最小相角系统而言，)(ωj G 曲线越靠近点（0,1j −），系统阶跃响应的振荡就越强烈，系统的相对稳定性就越差。
因此，可用)(ωj G 曲线对点（）的接近程度来表示系统的相对稳定性。
通常，这种接近程度是以相角裕度和幅值裕度来表的。
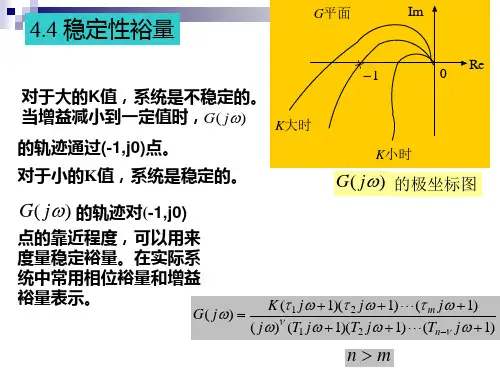
0,1j −相角裕度和幅值裕度是系统开环频率指标，它们与闭环系统的动态性能密切相关。
1．相角裕度相角裕度是指开环幅相频率特性)(ωj G 的幅值1)()(==ωωj G A 时的向量与负实轴的夹角，常用希腊字母γ表示。
图5-47 相角裕度和幅值裕度的定义 图 5-48 稳定裕度在Bode 图上的表示在G 平面上画出以原点为圆心的单位圆，见图5-47。
)(ωj G 曲线与单位圆相交，交点处的频率c ω称为截止频率，此时有1)(=c A ω。
按相角裕度的定义180()c γϕω=+o （5-69）由于01lg 20)(lg 20)(===c c A L ωω，故在伯德图中，相角裕度表现为dB L 0)(=ω处的相角)(c ωϕ与水平线之间的角度差，如图5-48所示。
上述两图中的o 180−γ均为正值。
2．幅值裕度)(ωj G 曲线与负实轴交点处的频率g ω称为相角交界频率，此时幅相特性曲线的幅值为)(g A ω，如图5-47所示。
幅值裕度是)(ωj G 与负实轴交点至虚轴距离的倒数，即1()g A ω，常用h 表示，即)(1g A h ω=（5-70）在对数坐标图上20lg 20lg ()()g g h A L =−ω=−ω （5-71）即的分贝值等于h )(g L ω与之间的距离（下为正）。
相位裕度增益裕度
相位裕度和增益裕度是电路稳定性分析中非常重要的指标。
它们分别
表示了电路输出信号的相位和增益与输入信号之间的差异，也就是说，它们衡量了电路对输入信号变化的响应能力。
一、相位裕度
相位裕度是指系统在增益等于1时，输出信号的相位与输入信号之间
的差异。
在Bode图中，相位裕度可以通过从幅频曲线上找到交点并
测量其左侧位置来计算。
具体来说，如果系统的幅频曲线在增益等于1时与负实轴之间有90度的距离，则该系统具有45度的相位裕度。
相位裕度越大，系统越稳定。
这是因为当系统受到外部扰动时，它需
要能够快速响应并保持输出信号与输入信号之间的相对位置。
如果相
位裕度不足，则可能会发生震荡或不稳定现象。
二、增益裕度
增益裕度是指系统在输出信号达到最大值前可承受多少衰减。
在Bode 图中，增益裕度可以通过从幅频曲线上找到交点并测量其右侧位置来
计算。
具体来说，如果系统的幅频曲线在相位裕度为45度时与-20dB
的水平线相交，则该系统具有20dB的增益裕度。
增益裕度越大，系统越稳定。
这是因为当系统受到外部扰动时，它需要能够快速响应并保持输出信号与输入信号之间的比例关系。
如果增益裕度不足，则可能会发生失真或不稳定现象。
综上所述，相位裕度和增益裕度都是电路稳定性分析中非常重要的指标。
它们可以用来衡量电路对输入信号变化的响应能力，并帮助工程师设计更加稳定和可靠的电路。
在实际应用中，工程师可以通过调整电路参数或使用反馈控制等技术来改善相位裕度和增益裕度，从而提高电路的性能和可靠性。
