柱锥台球的表面积

柱体、锥体、台体的表面积和体积【知识梳理】1．几种几何体的表面积公式图形表面积公式多面体多面体的表面积就是各个面的面积的和，也就是展开图的面积旋转体圆柱底面积：S底＝πr2侧面积：S侧＝2πrl表面积：S＝2πrl＋2πr2圆锥底面积：S底＝πr2侧面积：S侧＝πrl表面积：S＝πrl＋πr2圆台上底面面积：S上底＝πr′2下底面面积：S下底＝πr2侧面积：S侧＝πl(r＋r′)表面积：S＝π(r′2＋r2＋r′l＋rl)2．柱体的体积公式V＝Sh(S为底面面积，h为高)锥体的体积公式V＝13Sh(S为底面面积，h为高)台体的体积公式V＝13(S′＋S′S＋S)h【常考题型】题型一、柱、锥、台的表面积【例1】某几何体的三视图如图所示，该几何体的表面积是________．[解析]由三视图，画出几何体的直观图易求得基本量，如图所示，其表面积S＝2＋5×42×2＋4×(2＋4＋5＋5)＝28＋64＝92.[答案]92【类题通法】1．求几何体的表面积问题，通常将所给几何体分成基本几何体，再通过这些基本几何体的表面积进行求和或作差，从而获得几何体的表面积，另外有时也会用到将几何体展开求其展开图的面积进而得表面积．2．结合三视图考查几何体的表面积是高考的热点，解决此类问题的关键是正确地观察三视图，把它还原为直观图，特别要注意从三视图中得到几何体的相关量，再结合表面积公式求解．【对点训练】1．圆台的上、下底面半径分别是10 cm和20 cm，它的侧面展开图的扇环的圆心角是180°，求圆台的表面积．解：如图所示，设圆台的上底面周长为c cm，由于扇环的圆心角是180°，则c＝π·S A＝2π×10，解得SA＝20(cm)．同理可得SB＝40(cm)，所以AB＝SB－SA＝20(cm)．所以S表＝S侧＋S上＋S下＝π×(10＋20)×20＋π×102＋π×202＝1 100π(cm2).题型二、柱、锥、台的体积【例2】已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形，侧面是全等的等腰梯形，且侧面面积等于上、下底面面积之和，求棱台的高和体积．[解]如图所示，在三棱台ABC-A′B′C′中，O′、O分别为上、下底面的中心，D、D′分别是BC、B′C′的中心，则DD′是等腰梯形BCC′B′的高，所以，S侧＝3×12×(20＋30)×DD′＝75DD′.又A′B′＝20 cm，AB＝30 cm，则上、下底面面积之和为S上＋S下＝34×(202＋302)＝3253(cm2)．由S侧＝S上＋S下，得75DD′＝3253，所以，DD′＝1333(cm)．又∵O′D′＝36×20＝1033(cm)，OD＝36×30＝53(cm)，∴棱台的高h＝O′O＝D′D2－OD－O′D′2＝13332－53－10332＝43(cm)，由棱台的体积公式，可得棱台的体积为V＝h3(S上＋S下＋S上S下)＝433×(3253＋34×20×30)＝1 900(cm3)．【类题通法】求几何体的体积时，要注意利用好几何体的轴截面(尤其为圆柱、圆锥时)，准确求出几何体的高和底面积；同时，对不规则的几何体可利用分割几何体或补全几何体的方法转化为柱、锥、台体的体积计算问题．【对点训练】2．已知圆台的高为3，在轴截面中，母线AA1与底面圆直径AB的夹角为60°，轴截面中的一条对角线垂直于腰，求圆台的体积．解：如图所示，作轴截面A1ABB1，设圆台的上、下底面半径和母线长分别为r、R，l，高为h.作A1D⊥AB于点D，则A1D＝3.又∵∠A1AB＝60°，∴AD＝A1Dtan 60°，即R－r＝3×33，∴R－r＝ 3.又∵∠BA1A＝90°，∴∠BA1D＝60°.∴BD＝A1D·tan 60°，即R＋r＝3×3，∴R＋r＝33，∴R＝23，r＝3，而h＝3，∴V圆台＝13πh(R2＋Rr＋r2)＝13π×3×[(23)2＋23×3＋(3)2]＝21 π．所以圆台的体积为21 π．题型三、简单组合体的表面积和体积【例3】已知△ABC的三边长分别是AC＝3，BC＝4，AB＝5，以AB所在直线为轴，将此三角形旋转一周，求所得旋转体的表面积和体积．[解]如图，在△ABC中，过C作CD⊥AB，垂足为 D.由AC＝3，BC＝4，AB＝5，知AC2＋BC2＝AB2，则AC⊥BC.∵BC·AC＝AB·CD，∴CD＝125，记为r＝125，那么△ABC以AB所在直线为轴旋转所得旋转体是两个同底的圆锥，且底半径r＝12 5，母线长分别是AC＝3，BC＝4，所以S表面积＝πr·(AC＋BC)＝π×125×(3＋4)＝845π，V＝13πr2(AD＋BD)＝13πr2·AB＝13π×1252×5＝485π．所以，所求旋转体的表面积是845π，体积是485π．【类题通法】求组合体的表面积与体积的关键是弄清组合体中各简单几何体的结构特征及组合形式，对于与旋转体有关的组合体问题，要根据条件分清各个简单几何体的底面半径及母线长，再分别代入公式求解．【对点训练】3．某几何体的三视图如图所示，它的体积为()A．12πB．45πC．57πD．81π解析：选C由三视图可知，该几何体是由底面直径为6，高为5的圆柱与底面直径为6，母线长为5的圆锥组成的组合体，因此，体积为V＝π×32×5＋13×π×32×52－32＝57π．【练习反馈】1．若圆锥的高等于底面直径，则它的底面积与侧面积之比为() A．1∶2B．1∶ 3C．1∶ 5 D.3∶2解析：选C设圆锥底面半径为r，则高h＝2r，∴其母线长l＝5r.∴S侧＝πrl＝5πr2，S底＝πr2.2．若长方体的长、宽、高分别为 3 cm、4 cm、5 cm，则长方体的体积为() A．27 cm3B．60 cm3C．64 cm3D．125 cm3解析：选B长方体即为四棱柱，其体积为底面积×高，即为3×4×5＝60 cm3. 3．若圆锥的侧面展开图为一个半径为2的半圆，则圆锥的体积是________．解析：易知圆锥的母线长为2，设圆锥的半径为r，则2πr＝12×2π·２，∴r＝1，则高h＝l2－r2＝ 3.∴V圆锥＝13πr2·h＝13π×3＝33π．答案：3 3π4．圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，则圆台的侧面积为________．解析：已知圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，设圆台上底面的半径为r，则下底面半径和高分别为4r和4r，由100＝(4r)2＋(4r－r)2，得r＝2，故圆台的侧面积等于π(r＋4r)l＝π(2＋8)×10＝100π．答案：100π5．一个正三棱柱的三视图如图所示(单位：cm)，求这个正三棱柱的表面积与体积．解：由三视图知直观图如图所示，则高AA′＝2 cm，底面高B′D′＝2 3 cm，所以底面边长A′B′＝23×23＝4 cm.一个底面的面积为12×23×4＝4 3 cm2.所以S表面积＝2×43＋4×2×3＝(24＋83) cm2，V＝43×2＝8 3 cm3.所以表面积为(24＋83) cm2，体积为8 3 cm3.你曾落过的泪，最终都会变成阳光，照亮脚下的路。

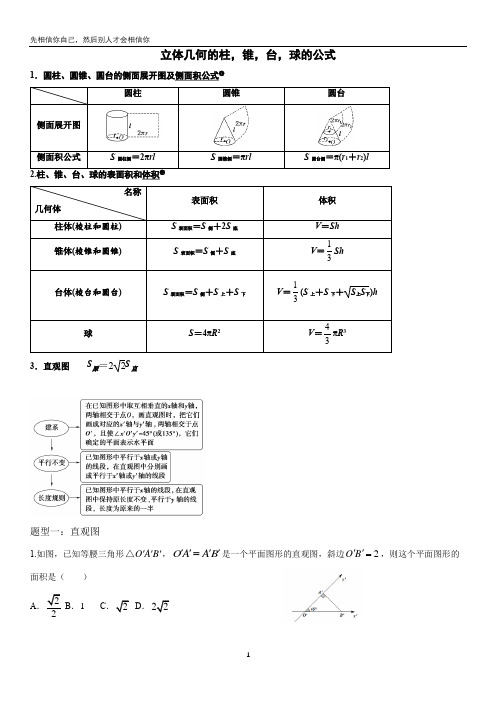
立体几何的柱，锥，台，球的公式1．圆柱、圆锥、圆台的侧面展开图及侧面积公式❶圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r 1＋r 2)l2.柱、锥、台、球的表面积和体积❷名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥)S 表面积＝S 侧＋S 底V ＝13Sh 台体(棱台和圆台) S 表面积＝S 侧＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h 球S ＝4πR 2V ＝43πR 3 3．直观图 S 原＝22S 直题型一：直观图1.如图，已知等腰三角形O A B '''△，OA AB ''''=是一个平面图形的直观图，斜边2O B ''=，则这个平面图形的面积是（ ） A ．22B ．1C ．2D ．222.一个梯形的直观图是一个如图所示的等腰梯形，且1A B ''=，3O C ''=，2O A ''=，则原梯形的面积为( )A ．22B ．42C ．8D ．43．如图所示为水平放置的正方形ABCO ，在平面直角坐标系xOy 中点B 的坐标为(2,2)，用斜二测画法画出它的直观图A ′B ′C ′O ′，则四边形A ′B ′C ′O ′的面积为___________.4．如图所示，是三角形ABC 的直观图，则三角形ABC 的面积S △ABC =_______；（请用数字填写）5．如图，正方形O ′A ′B ′C ′的边长为1，它是一个水平放置的平面图形的直观图，则原图形的周长为（ ） A ．4 B ．6C ．8D ．222+6.正三角形ABC 的边长为2 cm ，如图，△A’B’C’为其水平放置的直观图，则△A’B’C’的周长为（ ） A .8 cmB .6 cmC .（2 +√6）cmD .（2 + 2√3）cm7.用斜二测画法画出水平放置的△ABC 的直观图如图所示，已知A’C’ = 3，B’C’ = 2，则△ABC 中AB 边上的中线长为_________.8.(多空题)在如图所示的直观图中，四边形O ′A ′B ′C ′为菱形且边长为2 cm ，则在平面直角坐标系中原四边形OABC 为________(填具体形状)，其面积为________ cm 2.9．已知用斜二测画法得到的某水平放置的平面图形的直观图是如图所示的等腰直角△O B C '''，其中1O B ''=，则原平面图形中最大边长为( ) A ．2B ．22C ．3D ．2310.如图，△A ′B ′C ′表示水平放置的△ABC 根据斜二测画法得到的直观图，A B ''在x '轴上，B ′C ′与x '轴垂直，且2B C ''=，则△ABC 的边AB 上的高为（ ）A ．2B ．22C ．4D ．4211.如图所示，△A ′B ′C ′表示水平放置的△ABC 在斜二测画法下的直观图，A ′B ′在x ′轴上，B ′C ′与x ′轴垂直，且B ′C ′＝3，则△ABC 的边AB 上的高为（ ） A ．6√2 B ．3√3 C ．3√2 D ．3题型二棱柱、棱锥、棱台的表面积和体积1.正三棱锥的所有棱长均为a ，则该三棱锥的表面积为（ ） A .33a 2B .23a 2C .3a 2D .4a 22.已知正四棱锥的底面边长是2，侧棱长是5，则该正四棱锥的表面积为（ ） A .3B .12C .8D .433.已知高为3的棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形，如图，则三棱锥B -AB 1C 的体积为（ ） A .41 B .21 C .63 D .43 4.将一个棱长为a 的正方体，切成27个全等的小正方体，则表面积增加了（ ） A .26aB .212aC .218aD.224a5.将一个正方体截去四个角后得到一个正四面体，这个正四面体的体积是正方体体积的（ ）A .21 B .31 C .61 D .41 6.如图所示，在三棱台ABC - A 1B 1C 1中，A 1B 1：AB = 1：2，则三棱锥B - A 1B 1C 1与三棱锥A 1 - ABC 的体积比为（ ） A .1：2 B .1：3 C .1：2D .1：47.在底面半径为1的圆锥中，若该圆锥侧面展开图的面积是2π，则该圆锥的体积为（ ）A ．B ．C ．D ．8.已知球A 与球B 的体积之比为8：27，则球A 与球B 的半径之比为（ ） A ．：B ．4：9C ．2：3D ．3：29.球的一个截面面积为49πcm 2，球心到球截面距离为24cm ，则球的表面积是 ． 10.用一个平面截半径为25cm 的球，截面面积是49πcm 2，则球心到截面的距离是 ． 11.已知一个长方体的三个面的面积分别是2，3，6，则这个长方体的体积为_________。

课题：柱、锥、台、球的面积与体积一、知识点梳理1、多面体的表面积多面体的表面积是各个侧面的面积和底面面积的总和. 2、旋转体的表面积（1）圆柱的表面积公式S = （其中r 为底面半径，l 为母线长）. （2）圆锥的表面积公式S = （其中r 为底面半径，l 为母线长）.（3）圆台的表面积公式S = （其中/,r r 为上、下底面半径，l 为母线长）. （4）球的表面积公式S = （其中R 为球半径）. 3、几何体的体积公式（1）柱体的体积公式V = （其中S 为底面面积，h 为高）. （2）锥体的体积公式V = （其中S 为底面面积，h 为高）.（3）台体的体积公式V = （其中/S S 、为上、下底面面积，h 为高）. （4）球的体积公式V = （其中R 为球的半径）.二、基础巩固练习1、一个正三棱柱的三视图如右图所示，则这个正三棱柱的表面积 为 .2、棱长为1的正三棱锥的全面积是 .3、一张长、宽分别为8cm 和4cm 的矩形硬纸板，将这硬纸板折 成正四棱柱的侧面，则此四棱柱的对角线长为 .4、圆锥母线长6cm ，底面直径为3cm ，在母线SA 上有一点B ，AB =2cm ，那么由A 点绕圆锥侧面一周到B 点的最短距离为 .5、已知正四棱柱的底面面积为4，过相对侧棱的截面面积为8，则该正四棱柱的体积为 .6、一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1，2，3，则此球的表面积为 .7、将半径为R 的圆分割成面积之比为1：2：3的三个扇形作为三个圆锥的侧面，设这三个圆锥的底面半径依次为123,,r r r ，则123r r r ++的值为 .8、若正四棱锥的底面积是Q ，侧面积是S ，则它的体积为 .三、例题精选例1、一个正三棱锥的高和底面边长都为a ，求它的侧面积以及侧棱与底面所成的角.例2、将一个底面圆的直径为2，高为1的圆柱截成横截面为长方形的棱柱，设这个长方形截面的一条边长为x ，对角线长为2，截面的面积为A . （1）求面积A 的以x 为自变量的函数式；（2）求出截得棱柱的体积的最大值.例3、如图，一个倒圆锥形容器，它的轴截面是正三角形，在容器内放一个半径为r 的铁球，并向容器内注水，使水面恰好与铁球面相切.将球取出后，容器内的水深是多少？左视图 主视图俯视图 单位：mmA M CO 1 B O r例4、如图，在三棱柱111ABC A B C -中，底面是边长为a 的正三角形，且1AA 与,AC AB 所成角均为60︒，且1A A AB =，求该三棱柱的侧面积和体积例5、如图所示，等腰ABC ∆的底边AB =3CD =，点E 是线段BD 上异于点,B D 的动点，点F 在BC 边上，且EF AB ⊥.现沿EF 将BEF ∆折起到PEF ∆的位置，使.PE AE ⊥记,()BE x V x =表示四棱锥P ACFE -的体积.（1）求()V x 的表达式； （2）当x 为何值时，()V x 取得最大值.四、反馈练习1、正四棱台的上下底面边长分别为方程29180x x -+=的两根，其侧面积等于两底面积之和，则其高与斜高分别为 .2、正方体的全面积为2a ，它的顶点都在一个球面上，则这个球的表面积为 .3、体积为352cm 的圆台，一个底面面积是另一个底面面积的9倍，那么截得这个圆台的圆锥的体积为 .4、已知圆1O 是半径为R 的球O 的一个小圆，且圆1O 的面积与球O 的表面积的比值为29，则线段1OO 与R 的比值为 .5、已知正三棱锥P ABC -的外接球O 的半径为1，且满足0OA OB OC ++=，则正三棱锥P ABC -的体积为 .6、如图，已知正方体1111ABCD A B C D -的棱长为2，长为2的线段MN 的一个端点M 在楞1DD 上运动，点N 在正方形ABCD 内运动，则MN 中点P 的轨迹的面积是 .7、正三棱锥S ABC -中，M N 、分别是棱SC BC 、中点，MN AM ⊥，若SA =，则此三棱锥S ABC -外接球的表面积是 .8、已知直平行六面体1111ABCD A B C D -的各棱长均为3，60BAD ∠=︒，长为2的线段MN 的一个端点M 在1DD 上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点P 的轨迹（曲面）与其一顶点D 的三个面所围成的几何体的体积为 . 9、如图，线段AB α⊂平面，线段CD ⊂平面β，且平面//α平面,,,,AB CD AB CD a βαβ⊥==的距离为h ，求四面体ABCD 的体积.10 、已知正三棱柱的底面边长为1，侧棱长为2，这样的三棱柱能否放进一个体积为16π的小球？ ABC DOA 1B 1C 1A BC FE D PA 1ABCDB 1C 1D 1 M N AB CD βα。

柱,锥,台,球的表面积与体积【知识概述】空间几何体的表面积、体积是高考的必考知识点之一．题型既有选择题、填空题，又有解答题，难度为中、低档．客观题主要考查由三视图得出几何体的直观图，求其表面积、体积或由几何体的表面积、体积得出某些量；主观题考查比较全面，其中一步往往设置为表面积、体积问题，无论是何种题型都考查学生的空间想象能力．本节课通过知识的梳理和典型例题的讲解，使同学们理解和掌握空间几何体的表面积、体积的相关知识，并提高学生的空间想象能力、抽象概括能力、几何直观能力以及计算能力.1．柱、锥、台和球的侧面积和体积(1)棱柱、棱锥、棱台的表面积就是各面面积之和．(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形；它们的表面积等于侧面积与底面面积之和．【学前诊断】1. [难度]易已知圆锥的底面半径为2cm，高为，则该圆锥的体积为 .2．[难度] 中若某空间几何体的三视图如图所示，则该几何体的体积是（）A.2B.1C.2 3D.1 33．[难度]中若一个底面是正三角形的三棱柱的正视图如图所示,则其侧．面积．．等于( )AB．2C．D．6【经典例题】例1．将圆心角为2π3，面积为3π的扇形，作为圆锥的侧面，则圆锥的表面积等于______.例2．若某几何体的三视图（单位：cm）如下图所示，则此几何体的侧面积等于（）A. 212πcmB．215πcmC．224πcmD．230πcm例3．若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为________.例4．一个棱锥的三视图如图，则该棱锥的全面积(单位：cm2)为( )A. 48+B．48+C．36+D．36+例5．已知一个几何体的三视图如图所示，则此几何体的体积是________.例6．一个几何体的三视图如图所示，则这个几何体的体积等于（）A. 4BC．6D ．2例 7．如图是一个几何体的三视图，若它的体积是a =___________.例 8．将边长为a 的正方形ABCD 沿对角线AC 折起，使BD =a ，则三棱锥D-ABC 的体积为（ ）A.36aB.312aC.312a D.312a 例 9．有一根长为3π cm 、底面半径为1 cm 的圆柱形铁管，用一段铁丝在铁管上缠绕2圈，并使铁丝的两个端点落在圆柱的同一母线的两端，则铁丝的最短长度为多少？ 【本课总结】1．面积、体积的计算中应注意的问题(1)柱、锥、台体的侧面积分别是某侧面展开图的面积，因此，弄清侧面展开图的形状及各线段的位置关系，是求侧面积及解决有关问题的关键．(2)计算柱、锥、台体的体积关键是找到相应的底面积和高．充分运用多面体的截面及旋转体的轴截面，将空间问题转化成平面问题．(3)球的有关问题，注意球半径与截面圆半径，球心到截面距离构成直角三角形． (4)有关几何体展开图与平面图形折成几何体问题，在解决的过程中注意按什么线作轴来展或折，还要坚持被展或被折的平面，变换前、后在该面内的大小关系与位置关系不变．在完成展或折后，要注意条件的转化对解题也很重要． 2．与球有关的组合体问题与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径．球与旋转体的组合，通常作它们的轴截面进行解题，球与多面体的组合，通过多面体的一条侧棱和球心，或“切点”、“接点”作出截面图． 【活学活用】 1．[难度] 中若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（ ）1A CBA.3523cm 3B. 3203cm 3C. 2243cm 3D. 1603cm 32. [难度] 难如图，正方体1111ABCD-A B C D 的棱长为2，动点E 、F 在棱11A B 上.点Q 是CD 的中点动点P 在棱AD 上，若EF =1，DP=x ，1A E=y (x,y 大于零)，则三棱锥P-EFQ 的体积： A. 与x ，y 都有关； B. 与x ，y 都无关；C.与x 有关，与y 无关；D. 与y 有关，与x 无关； 3. [难度] 中一个几何体的三视图如图，该几何体的表面积为( ).A.280B. 292C. 360D. 372。

1.1.6 柱、锥、台、球的表面积【学习目标】理解公式的推导并会求柱、锥、台、球的表面积。

【重点】柱、锥、台、球的表面积 【难点】计算侧面积【自主学习】1.直棱柱和正棱锥的侧面展开图各是什么？球能展成平面图吗？2.利用直棱柱的侧面展开图,可以得到直棱柱的侧面积公式是什么？全面积呢？=直棱柱侧面积S3.同理 正棱锥和正棱台的侧面积及全面积公式各是什么？=正棱锥侧面积S =正棱台侧S4．球的表面积公式是什么？=球S5.利用直棱柱、正棱锥、正棱台的侧面积的求法,你能否说出圆柱、圆锥、圆台的 侧面积的求法,及侧面积和全面积公式是什么?=圆柱S ；=圆锥S【典例解析】例1、已知正四棱锥底面正方形的边长为4cm ，高与斜高的夹角为045，求正四棱锥的侧面积及全面积（单位：2cm ）变式1.一个正三棱锥的侧面都是正三角形,侧棱长为4,求它的侧面积和全面积。

变式2.若一个正三棱台的两个底面边长分别等于4cm 和8cm, 侧棱长为8cm, 求它的全面积例2. (1)若正三棱锥的斜高是棱锥高的332倍，则正棱锥的侧面积是底面积的（ ） A32 倍 B 2 倍 C 38 倍 D 3 倍(2)已知正三棱台的上底面边长为2，下底面边长为4，高为315，则正三棱台的侧面积S 1与两底面面积之和S 2的大小关系为（ ） A S 1 〉 S 2 B S 1〈 S 2 C S 1 = S 2 D 以上都不对【达标检测】1．已知正方体的对角线为a ，则正方体的全面积是（ ）A 222aB 22aC 232aD 223a2．若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积为（ ）A 3πB 33πC 6 πD 9π3．长方体一个顶点上三条棱长分别为3、 4 、5 ,且它的八个顶点都在同一球面上,则这个球的表面积是( )Ａ 20π2 Ｂ25π2 Ｃ50π Ｄ 200π4.已知火星的半径是地球的一半,则地球表面积是火星表面积的 倍.5. 某地球仪上北纬30︒纬线的长度为12πcm ，该地球仪的半径是 cm ，表面积是 cm 2。