下载文档原格式
5.5 稳定裕度5.5.1 稳定裕度的定义控制系统稳定与否是绝对稳定性的概念。
而对一个稳定的系统而言，还有一个稳定的程度，即相对稳定性的概念。
相对稳定性与系统的动态性能指标有着密切的关系。
在设计一个控制系统时，不仅要求它必须是绝对稳定的，而且还应保证系统具有一定的稳定程度。
只有这样，才能不致因系统参数的小范围漂移而导致系统性能变差甚至不稳定。
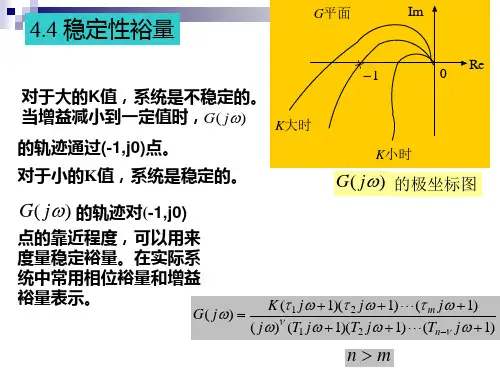
对于一个最小相角系统而言，)(ωj G 曲线越靠近点（0,1j −），系统阶跃响应的振荡就越强烈，系统的相对稳定性就越差。
因此，可用)(ωj G 曲线对点（）的接近程度来表示系统的相对稳定性。
通常，这种接近程度是以相角裕度和幅值裕度来表的。
0,1j −相角裕度和幅值裕度是系统开环频率指标，它们与闭环系统的动态性能密切相关。
1．相角裕度相角裕度是指开环幅相频率特性)(ωj G 的幅值1)()(==ωωj G A 时的向量与负实轴的夹角，常用希腊字母γ表示。
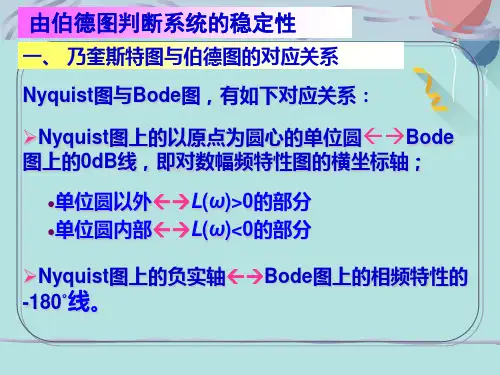
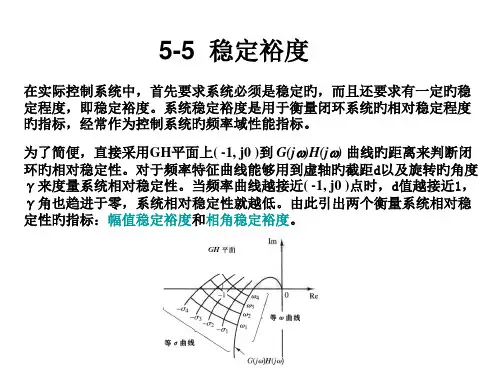
图5-47 相角裕度和幅值裕度的定义 图 5-48 稳定裕度在Bode 图上的表示在G 平面上画出以原点为圆心的单位圆，见图5-47。
)(ωj G 曲线与单位圆相交，交点处的频率c ω称为截止频率，此时有1)(=c A ω。
按相角裕度的定义180()c γϕω=+o （5-69）由于01lg 20)(lg 20)(===c c A L ωω，故在伯德图中，相角裕度表现为dB L 0)(=ω处的相角)(c ωϕ与水平线之间的角度差，如图5-48所示。
上述两图中的o 180−γ均为正值。
2．幅值裕度)(ωj G 曲线与负实轴交点处的频率g ω称为相角交界频率，此时幅相特性曲线的幅值为)(g A ω，如图5-47所示。
幅值裕度是)(ωj G 与负实轴交点至虚轴距离的倒数，即1()g A ω，常用h 表示，即)(1g A h ω=（5-70）在对数坐标图上20lg 20lg ()()g g h A L =−ω=−ω （5-71）即的分贝值等于h )(g L ω与之间的距离（下为正）。
相角裕度大于0系统稳定吗
常用波特图来描述频率响应，对于稳定性的判定会有两个参数，那就是幅值裕度和相角裕度，通常情况下，利用后者进行判定，但是对于幅值裕度，指的是相角为-180度时对应的幅值（这里是dB）。
扩展资料
波德图是闭环动态控制系统稳定性的量度。
相位裕度能够表现相对稳定性（其对于阶跃函数等输入变化的阻尼响应振荡的倾向）。
增益裕度能够表现绝对稳定性和给定任意干扰，不加限制，系统会振荡的程度。
波德图是由贝尔实验室的荷兰裔科学家亨德里克·韦德·波德在1930年发明。
波德用简单但准确的方法绘制增益及相位的图，因此他发明的图也就称为波德图。
波德图幅频图的频率用对数尺度表示，增益部分一般都用功率的分贝值来表示，也就是将增益取对数后再乘以20。
由于增益用对数来表示，因此一传递函数乘以一常数，在波德增益图只需将图形的纵向移动即可，二传递函数的相乘，在波德幅频图就变成图形的相加。
幅频图纵轴0分贝以下具有正增益裕度、属稳定区，反之属不稳定区。
