截面法求内力解析
- 格式:ppt
- 大小:1.71 MB
- 文档页数:20

浅探内力分析之截面法摘要: 材料力学离不开内力分析,截面法更是求内力的一般方法,在展开工程设计时,如果建筑的受力分析准确性得不到保障,那么建筑的安全性和耐久性等就会出现问题。
本文从截面法对不同种内力的具体应用进行初步研究寻找其计算方法。
关键词: 材料力学;内力;截面法引言在工程设计过程中会运用许多的理论力学知识,截面法便是其中至关重要的一种,且短时间内难以被取代,因此截面法受到广泛运用。
本文即从截面法对不同种内力的具体应用题展开计算分析。
1 截面法1.1 截面法的定义截面法:用截面假想地把构件分成两部分,以此来分析明确内力大小,并以平衡条件确定其合力的方法。
1.2 截面法的研究对象内力:物体在受到外力作用而变形时,其内部各质点间的相对位置将发生变化。
相应地,各质点间的相互作用力也将发生改变。
这种由外力作用而引起的质点间相互作用力的改变量,即为材料力学中所研究的内力。
1.3 截面法的步骤主要分以下三个步骤:1、截开:在需要求内力的截面处,假想地将杆分为两部分;2、代替:将两部分中的任意一部分留下,把弃去部分对留下部分的作用,以作用在截面上的内力(力或力偶)代替;3、平衡:对留下部分建立平衡方程,根据上面的已知外力来计算杆件在截开面上的未知内力。
注意,截开面上的内力对留下部分而言已属外力。
图 12 轴力与杆件轴线相重合的内力,称为轴力,用符号FN表示。
轴力的正负规定: 当轴力的指向离开截面时,杆受拉,规定轴力为正;反之,当轴力指向截面时,杆受压,规定轴力为负。
即拉为正,压为负。
2.1 轴力分析计算已知F1=4OKN,F2=-30KN,求AB杆的内力。
应用截面法求杆件横截面上的内力,如图2所示。
截开:用假想平面m-m将构件切开分为两部分。
代替:取出其中任一部分如I部分为研究对象,画出I部分的受力图平衡:列出Ⅰ部分的平衡方程式:由∑Fx=0,得Fx-F=0,得FN=F1=4OKN(背离横截面,拉力为正)求BC杆的内力。

试述求杆件横截面上内力的截面法步骤和方法1. 了解截面法哎,说到工程力学里的截面法,别让这些名字吓坏了,其实就是一种找出杆件内部力量的简单方法。
咱们平常接触的建筑物、桥梁,或者一些机械构件,都是通过这种方法来确保它们的稳固和安全的。
这个方法简单来说就是用“剪刀”切一刀,把杆件“分尸”,然后分析切面上受力的情况。
好比是咱们剥苹果皮,剥开之后看里面的果肉,这样能更清楚地了解苹果的质量。
2. 截面法的步骤2.1 选取截面首先,挑选一个合适的截面,瞅准了方向之后,就下手了。
这个步骤就像在你脑子里画出一条切割线。
你得选择一个合适的位置,把杆件从中间“切开”。
这里要注意,选取的位置一定要使得切面上的力易于计算。
如果这个位置选错了,结果就像你在黑暗中找钥匙一样,费劲不讨好。
2.2 画出受力图接下来,别忘了给这片“切面”画上图。
要把杆件切开后,分离出的部分的受力情况画出来。
图上得标明各种内力,比如剪力、轴力和弯矩等等。
这些力就像是在打游戏时,你需要记录你的角色的状态和装备一样,你要准确记录这些力的情况,这样才能确保你计算的准确。
2.3 列出平衡方程然后,你就要写平衡方程了。
平衡方程是用来保证杆件在切开时的受力状态是平衡的,不会乱七八糟。
这些方程包括了力的平衡、力矩的平衡等。
就像你玩积木,如果要保持积木塔不倒,就得仔细计算每一块积木的放置位置。
2.4 解方程找内力最后,你要解这些方程,找出杆件内部的力量。
就像做数学题一样,把方程算出来,你就能得到具体的内力数值。
这个步骤可不能马虎,不然得到的结果就像是空话,没有实际意义。
3. 截面法的应用3.1 结构分析截面法在结构分析中的应用非常广泛。
无论是大桥、小楼,还是家里的门框,都是用这个方法来确保结构的安全性。
就像是大厨做菜,得先知道每种材料的用量和比例,才能做出美味的菜肴。
工程师用截面法就像是这个大厨,通过计算内力,确保建筑的稳定性和安全性。
3.2 机械设计在机械设计中,截面法也是必不可少的。


一、概述截面法是工程力学中用于求解杆件内力的基本方法之一。
在工程结构分析和设计中,了解截面法的原理和应用是至关重要的。
本文将深入探讨截面法的基本概念、原理和应用,以帮助读者更好地理解和应用这一方法。
二、截面法的基本概念1.1 概念简介截面法是工程力学中用于分析杆件内力的一种方法,它基于杆件内力平衡的原理,通过考察杆件的截面上的内力分布情况来求解杆件的内力。
1.2 截面法的基本原理截面法基于力的平衡原理,即在杆件的截面上,杆件的内力必须满足横向平衡和转矩平衡的条件。
通过分析截面上的内力分布情况,可以确定杆件内的弯矩、剪力和轴力。
1.3 截面法的应用范围截面法适用于各种杆件的内力分析,包括梁、柱、桁架等结构中的杆件。
在工程实践中,截面法常常用于分析结构内部的受力情况,为结构设计和分析提供重要依据。
三、截面法的具体步骤2.1 确定截面在应用截面法时,首先需要确定分析的截面位置。
通常情况下,选择距离受力部位较近的位置作为截面。
2.2 绘制内力图在截面上绘制出杆件内的剪力图和弯矩图,根据平衡条件和力学原理,确定内力的方向和大小。
2.3 计算内力根据绘制的剪力图和弯矩图,可以直接求解出截面上的剪力、弯矩和轴力大小。
这些内力是杆件在该截面上的受力情况的表示。
2.4 检验平衡通过检验内力图的平衡条件,验证所得的内力是否符合力学平衡定律。
如果内力满足平衡条件,则认为截面法计算是正确的。
四、截面法的应用举例3.1 梁的截面力分析以简支梁为例,说明如何利用截面法分析梁的内力情况。
根据距离支座较近的位置选择截面,绘制剪力图和弯矩图,并计算出截面上的内力情况。
3.2 柱的截面力分析以等截面柱为例,说明如何利用截面法分析柱的内力情况。
通过选择适当位置的截面,绘制出内力图,计算出截面上的轴力和弯矩。
五、截面法的优缺点4.1 优点截面法简单直观,易于理解和应用。
通过截面法可以直接得到截面上的内力分布情况,为结构的受力分析提供了重要依据。
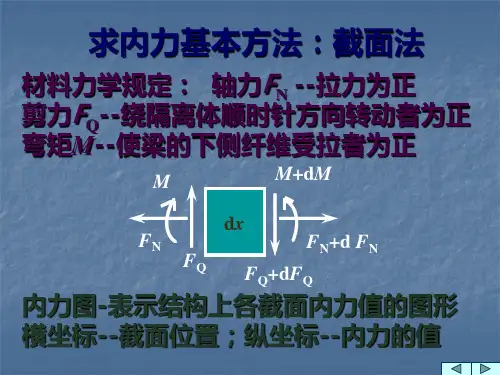

截面法求内力的步骤简介截面法是一种用于计算结构内力的方法,广泛应用于工程领域。
它通过将结构切割成若干个截面,分析每个截面上的受力情况,从而确定结构中各个部分的内力分布。
本文将详细介绍截面法求内力的步骤,包括确定切割截面、计算受力平衡、绘制剪力图和弯矩图等内容。
步骤一:确定切割截面在进行截面法计算之前,首先需要确定切割截面的位置。
通常情况下,选择合适的切割截面位置可以简化计算,并且使得结果更加准确。
切割截面的位置应该选择在结构受力变化较大或者存在集中荷载作用的地方。
步骤二:计算受力平衡在确定了切割截面之后,需要对每个切割截面进行受力平衡计算。
根据静力平衡原理,对于一个处于静止状态的结构,在任意一个切割截面上受到的外部作用力和内部反作用力之和应该为零。
可以利用受力平衡方程来计算切割截面上的内力。
步骤三:绘制剪力图剪力是指结构中某一截面上的内力,它与截面上的受力平衡有关。
在截面法求解内力时,常常需要绘制剪力图。
剪力图是以结构轴线为横坐标,剪力值为纵坐标的图形表示。
绘制剪力图的步骤如下:1.选择合适的坐标系,通常选取结构轴线作为横坐标。
2.根据受力平衡计算出每个切割截面上的剪力值。
3.将计算得到的剪力值绘制在相应位置上。
4.连接各个点,即可得到完整的剪力图。
步骤四:绘制弯矩图弯矩是指结构中某一截面上的内力,它与截面上的受力平衡和几何形状有关。
在截面法求解内力时,常常需要绘制弯矩图。
弯矩图是以结构轴线为横坐标,弯矩值为纵坐标的图形表示。
绘制弯矩图的步骤如下:1.选择合适的坐标系,通常选取结构轴线作为横坐标。
2.根据受力平衡和几何形状计算出每个切割截面上的弯矩值。
3.将计算得到的弯矩值绘制在相应位置上。
4.连接各个点,即可得到完整的弯矩图。
步骤五:计算其他内力除了剪力和弯矩之外,还有其他一些常见的内力需要计算,如轴力、扭矩等。
根据受力平衡和结构几何形状,可以通过类似的方法计算出这些内力,并绘制相应的图形。
步骤六:分析结果在完成内力计算之后,需要对结果进行分析。



构件内力的求解用截面法。
构件内力的求解是工程力学中的一个重要问题。
截面法是一种常见的求解构件内力的方法之一。
本文将详细介绍截面法的基本原理和具体应用。
截面法的基本原理是基于静力学平衡条件,即在任何一个截面上,作用在该截面上的剪力、弯矩和轴力之和等于零。
因此,对于任意一个构件,只要确定其受力状态,就可以通过截面法求解出其各个截面上的内力。
截面法的求解过程通常分为以下几步:1. 确定截面:根据受力情况,选择需要求解的截面。
2. 切割构件:将构件沿着所选截面切割成两个或多个部分,形成一个自由体和一个受力体。
3. 建立平衡方程:对自由体和受力体分别建立平衡方程,其中包括剪力平衡、弯矩平衡和轴力平衡等。
4. 求解内力:通过求解平衡方程,计算出所选截面上的剪力、弯矩和轴力等内力。
5. 绘制内力图:根据所求得的内力,绘制出相应的内力图,以便于分析和设计。
截面法的具体应用广泛,常见的应用包括:1. 梁的内力求解:对于梁受到的外力和支反力情况,可以通过截面法求解出其各个截面上的剪力、弯矩和轴力等内力,从而进行梁的设计和分析。
2. 框架结构的内力求解:对于框架结构,可以通过截面法求解出每个构件的内力,从而得到结构的整体受力情况,进行结构的设计和分析。
3. 桥梁结构的内力求解:对于桥梁结构,可以通过截面法求解出桥梁各个截面的内力,从而进行桥梁的设计和分析。
例如,可以确定桥梁的最大荷载能力和最大跨度等参数。
截面法是一种常见的求解构件内力的方法,其基本原理是基于静力学平衡条件,通过建立平衡方程,计算出所选截面上的剪力、弯矩和轴力等内力。
在工程实践中,截面法被广泛应用于梁、框架结构和桥梁等工程领域。
简述截面法计算内力的步骤
截面法是一种结构力学分析的方法,用于计算结构中截面处的内力。
以下是使用截面法计算内力的步骤:
1. 确定截面:根据结构的几何形状和所需计算的截面位置,确定需要计算的截面。
2. 建立截面坐标系:在确定的截面处,建立适当的坐标系,通常使用弯矩轴线和剪力轴线作为坐标轴。
3. 计算剪力:在截面上计算受力情况,包括剪力和轴向力。
剪力可以通过受力平衡或应力分布方法进行计算。
4. 计算弯矩:在截面上计算受力情况,包括弯矩和轴向力。
弯矩可以通过弯曲公式和应力分布方法进行计算。
5. 绘制剪力图和弯矩图:根据计算得到的剪力和弯矩在截面上的分布情况,绘制剪力图和弯矩图。
6. 分析内力:根据截面上的剪力和弯矩分布,分析各个部分的内力情况,包括剪力内力和弯矩内力。
7. 分析截面的承载力:根据截面的几何特性和材料的强度,分析截面的承载力情况,包括抗弯承载力和抗剪承载力。
通过以上步骤,可以得到截面处的剪力和弯矩分布情况,以及
各个部分的内力情况。
这些结果可以用于结构设计和分析中的其他计算和决策。
截面法1截面法可以快速求出某一内力,通常取结构 的一部分为隔离体,其上力系为平面一般力系。
每个隔离体上有3个独立平衡方程。
一般表示 为: ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点: 尽量使一个方程解一个未知数,避免求解 联立方程。
一. 力矩法例:求图示桁架1、2、3杆的轴力。
2VAVB解:由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。
Ⅰ3Ⅰ(1)求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。
N1 对K1点取矩,由 ∑MK1 = 0 从而求出所求未知 力N1。
VA(2)求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。
2杆轴力N2(3)求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。
3杆轴力N3力矩法要点:7欲求某指定杆内力,则作一截面,截开待求 杆; 隔离体上除所求未知力外,其余未知力的延 长线均交于某一点K。
对K点取矩,从而求出所求未知力 。
(1)选择其余未知力延长线的交点K作为取矩 点,从而用∑MK=0,求出指定杆内力。
(2)将斜杆的内力放在某一个合适的点上分 解,使其一个分力通过取矩点K。
例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时,对另 外两个未知力的 交点C取矩,10C由 ΣMc=0,得 Na×4+30×8=030kN解得: Na =- 60kN求NbD Xb E Yb Nb30kN11求Nb时,对点D取矩。
将Nb 其在E点处分解 为水平和竖向分量。
由ΣMD=0,得 Yb×12+40×4 - 30×12=0 解得 Yb=16.67 kN由比例关系得到:N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时,对点E取矩。