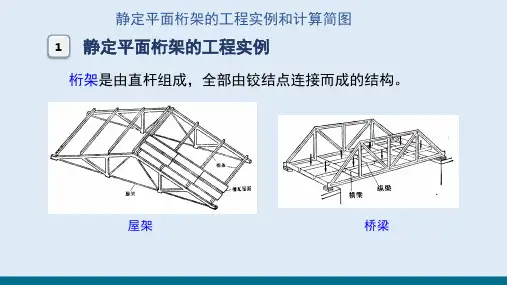
例题-桁架-截面法

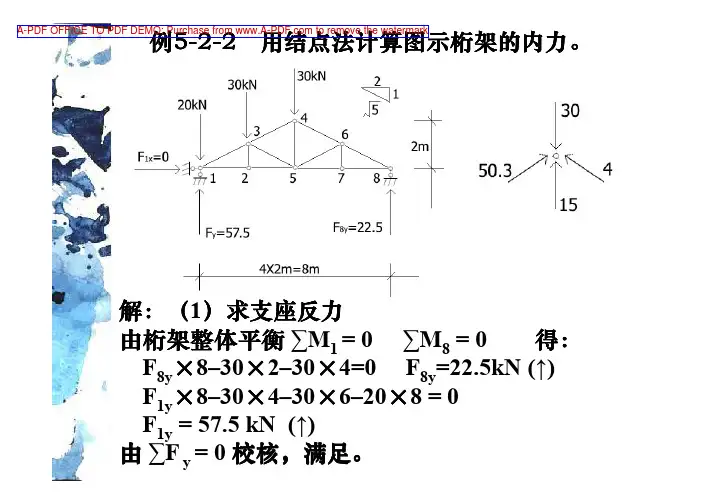
例5-2-2用结点法计算图示桁架的内力用结点法计算图示桁架的内力。

解：（1）求支座反力由桁架整体平衡∑M 1 = 0 ∑M 8= 0 得：F 8y ×8–30×2–30×4=0 F 8y =22.5kN (↑)F 1y ×8–30×4–30×6–20×8 = 0F 1y = 57.5 kN (↑)由∑F y = 0 校核校核，，满足满足。

A-PDF OFFICE TO PDF DEMO: Purchase from to remove the watermark(2) 求各杆轴力由结点法的特殊情况判断出零杆为由结点法的特殊情况判断出零杆为：：杆23, 杆67, 杆57。

其它杆力计算如下其它杆力计算如下：：结点8: ∑F y =0 F 86y = –22.5 kNF N86=(F 86y /l 86y )×l 86= –50.3 kNF 86x =(F 86y /l 86y )×l 86x = –45 kN∑F x =0F N87=45kN F N46=F N86= –50.3kNFN57=F N87=45kN结点结点１１: ∑F y =0 F 13y =20–57.5= –37.5kNF N13=(F 13y /l13y )×l 13= –83.9 kNF 13x =(F 13y /l 13y )×l 13x = –75 kN∑F x =0FN1 =75 kNF N25=F N12=75kN结点3: ∑M = 04F 35x ×2+30×2–37.5×4+75×2=0 F 35x = –30kN F N35=(F 35x /l 35x )×l 35= –33.5 kNF 35y =(F 35x /l 35x )×l 35y = –15 kN∑M 5 = 0 F 34x ×2–30×2+37.5×4 =0F 34x = –45kNF N34=(F 34x /l 34x )×l 34= –50.3 kNF 34y =(F 34x /l 34x )×l 34y = –22.5 kN结点结点５５: ∑F y =0F N54=15kN 由结点由结点４４∑F = 0校核校核，，满足满足。

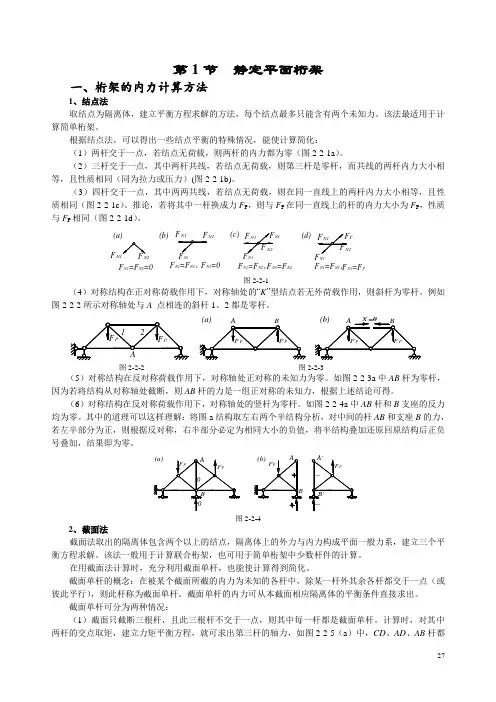
第1节 静定平面桁架一、桁架的内力计算方法1、结点法取结点为隔离体，建立平衡方程求解的方法，每个结点最多只能含有两个未知力。

该法最适用于计算简单桁架。

根据结点法，可以得出一些结点平衡的特殊情况，能使计算简化：（1）两杆交于一点，若结点无荷载，则两杆的内力都为零（图2-2-1a ）。

（2）三杆交于一点，其中两杆共线，若结点无荷载，则第三杆是零杆，而共线的两杆内力大小相等，且性质相同（同为拉力或压力）(图2-2-1b)。

（3）四杆交于一点，其中两两共线，若结点无荷载，则在同一直线上的两杆内力大小相等，且性质相同（图2-2-1c ）。

推论，若将其中一杆换成力F P ，则与F P 在同一直线上的杆的内力大小为F P ，性质与F P 相同（图2-2-1d ）。

F N3F N3=0F N1=F N2=0F N3=F N4(a)(b)(c)F N4(d)F N3=F PF PN1F F N2F N1F N2F N1F N2F N1F N2F N3F N3F N1=F N2，F N1=F N2，F N1=F N2，图2-2-1（4）对称结构在正对称荷载作用下，对称轴处的“K ”型结点若无外荷载作用，则斜杆为零杆。

例如图2-2-2所示对称轴处与A 点相连的斜杆1、2都是零杆。

1A2F PF PAF PF PBF PF PBA(b)(a)X =0图2-2-2 图2-2-3（5）对称结构在反对称荷载作用下，对称轴处正对称的未知力为零。

如图2-2-3a 中AB 杆为零杆，因为若将结构从对称轴处截断，则AB 杆的力是一组正对称的未知力，根据上述结论可得。

（6）对称结构在反对称荷载作用下，对称轴处的竖杆为零杆。

如图2-2-4a 中AB 杆和B 支座的反力均为零。

其中的道理可以这样理解：将图a 结构取左右两个半结构分析，对中间的杆AB 和支座B 的力，若左半部分为正，则根据反对称，右半部分必定为相同大小的负值，将半结构叠加还原回原结构后正负号叠加，结果即为零。

截面法‹1截面法可以快速求出某一内力，通常取结构 的一部分为隔离体，其上力系为平面一般力系。

每个隔离体上有3个独立平衡方程。

一般表示 为： ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点： 尽量使一个方程解一个未知数，避免求解 联立方程。

一. 力矩法例：求图示桁架1、2、3杆的轴力。

2VAVB解：由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。

Ⅰ3Ⅰ（1）求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。

N1 对K1点取矩，由 ∑MK1 = 0 从而求出所求未知 力N1。

VA（2）求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。

2杆轴力N2（3）求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。

3杆轴力N3力矩法要点：„7„„欲求某指定杆内力，则作一截面，截开待求 杆； 隔离体上除所求未知力外，其余未知力的延 长线均交于某一点K。

对K点取矩，从而求出所求未知力 。

（1）选择其余未知力延长线的交点K作为取矩 点，从而用∑MK=0，求出指定杆内力。

（2）将斜杆的内力放在某一个合适的点上分 解，使其一个分力通过取矩点K。

例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时，对另 外两个未知力的 交点C取矩，10C由 ΣMc＝0，得 Na×4＋30×8＝030kN解得： Na =－ 60kN求NbD Xb E Yb Nb30kN11求Nb时，对点D取矩。

将Nb 其在E点处分解 为水平和竖向分量。

由ΣMD＝0，得 Yb×12＋40×4 － 30×12＝0 解得 Yb＝16.67 kN由比例关系得到：N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时，对点E取矩。

结构力学桁架截面法例题
结构力学桁架截面法例题
一、题目：
一根钢桁架有两种不同截面，桁架长度为3m，端部修里夹具为α=60°，桁架的两个截面信息如下：
截面1：
a1=20mm，b1=10mm，I1=40×104mm4
截面2：
a2=50mm，b2=20mm，I2=500×104mm4
请用桁架截面法计算其承载力。

二、解答：
1、计算桁架的顶点角度θ和抗弯矩Mx：
利用转矩定理，可以得到桁架承载力P的表达式：
P=Mx/l*cosθ
用已知量计算得θ=30°，Mx=12.33×104N·m
2、求解桁架的承载力P：
将计算得的θ和Mx代入表达式：
P=12.33×104N·m/3m*cos30° = 4.11×104N
3、计算桁架的屈曲应力σbb：
利用屈曲应力的表达式：
σbb=Mx/S
用已知量计算得S=12.5×104mm2，σbb=0.99MPa。

以上便是本题的答案。

桁架承载力P=4.11×104N，屈曲应力σbb=0.99MPa。

简单平面桁架受力分析仪22 廖嵩松 020854内容摘要：桁架使工程中常用的一种结构，求解桁架受力有三种方法：虚位移法、节点法、截面法,他们个又有缺点，适用于不同情况，更多情况是将它们综和运用。

关键词：桁架——虚位移法——节点法——截面法—-载荷参考书目：李俊峰，张雄,任革学,高云峰编．理论力学．北京：清华大学出版社,2001西北工业大学理论力学教研室编．和兴锁主编．理论力学．西安：西北工业大学出版社,2001 牛学仁主编．理论力学．北京：机械工业出版社,2000一、 桁架简化模型桁架是工程中常用的一种结构，各构件在同一平面内的桁架称为平面桁架。

简单平面桁架是指在一个基本三角框架上每增家两各杆件的同时增加一个节点而形成的桁架.它始终保持其坚固性，且在这种桁架中除去任何一个杆件都会使桁架失去稳固性。

在简单平面桁架中，杆件的数目m 与节点数目n 之间有确定关系。

基本三角框家的杆件书和节点数都等于3。

此后增加的杆件数（m-3）节点数(n-3）之间的比例是2：1，故有 323-=-n m 即n m 23=+ 在计算载荷作用下平面桁架各杆件的所受力时,为简化计算，工程上一般作如下规定：（1） 各杆件都是直杆，并用光滑铰链连接；（2） 杆件所受的外载荷都作用在各节点上,各力作用线都在桁架平面内；（3） 各杆件的自重忽略不计;在以上假设下，每一杆件都是二力构件，故所受力都沿其轴线，或为拉力，或为压力。

为便于分析,在受力图中总是假设杆件承受拉力，若计算结果为负值，则表示杆件承受压力。

二、 计算桁架受力的三种方法1、 虚位移法接触所求杆的约束，用约束反力代替，系统仍处于平衡状态，但有一个自由度.假设系统沿此自由度的方向有一微小的运动，可得出各主动力作用点及所加约束力的一组虚位移，根据虚位移原理可列出一个方程，解出约束反力的大小。

例1．求解图1所示平面桁架中1杆的约束力.解：去掉1杆,用N1和N1’代替。

假设EFG 绕F 转一小角度δθ，则),cos (sin ,30tan ,0j i a r i a r r D E C•-•=•︒==θθδθδδθδδ 2、节点法桁架处于平衡状态，它的各个节点也一定是平衡的.可以通过研究各个节点的平衡求出相应杆的内力。