截面法求内力
- 格式:ppt
- 大小:1.71 MB
- 文档页数:20

截面法求杆件的内力教学目标:1、理解和掌握求杆件内力的方法——截面法;2、熟练运用截面法求不同杆件受到拉伸时的内力。
教学重点:截面法求杆件内力的步骤。
教学难点:如何运用截面法求内力的方法解决工程力学中求内力的实际问题。
教学方法:提出问题——实例演示——练习点拨——归纳总结教学过程:一、复习旧知1、杆件有哪几种基本变形?2、拉伸和压缩的受力特点是什么?3、拉伸和压缩的变形特点是什么?二、新课讲解思考:当杆件受到拉伸、压缩时,就会在杆件内部产生力的作用,怎样才能确定杆件的内部会产生多大的力?(引出课题)出示本节课的学习目标。
(一)、教学什么是杆件的内力?内力:杆件在外力作用下产生变形,其内部相互间的作用力称为内力。
一般情况下,内力将随外力增加而增大。
当内力增大到一定限度时,杆件就会发生破坏。
内力是与构件的强度密切相关的,拉压杆上的内力又称为轴力。
(二)、教学截面法求杆件的内力。
1、什么是截面法?截面法:将受外力作用的杆件假想地切开,用以显示内力的大小,并以平衡条件确定其合力的方法,称为截面法。
它是分析杆件内力的唯一方法。
2、实例演示:如图AB 杆受两个力,一个向左,一个向右,大小均为F 。
作用点分别为A 和B 。
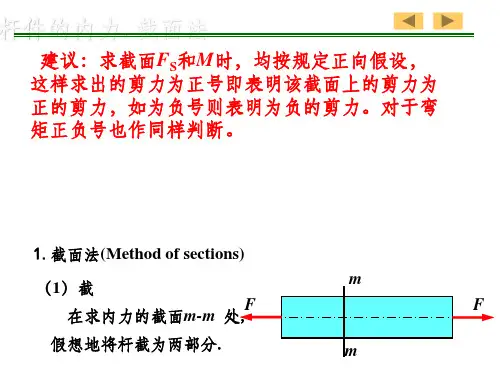
①、确定要截开的次数和位置(要根据杆件的受力情况而定) ②、选取一半截面为研究对象(一般选取受力较少的一段作为研究对象)③、假设出截面上的内力(取左段内力向右设,取右段内力向左设,方向跟坐标轴方向一致,左负右正、下负上正)④、用平衡方程求出截面上的内力(求出的内力为正值为拉力,负值为压力)取左段 ∑Fx=O -F +FN =0 取右段 ∑Fx=O F -FN =0FN =F FN =F 3、总结截面法求杆件内力的步骤:(1)截:在需求内力的截面处,沿该截面假想地把构件切开。
(2)取:选取其中一部分为研究对象。
(3)代:将截去部分对研究对象的作用,以截面上的未知内力F F N来代替。
(4)平:根据研究对象的平衡条件,建立平衡方程,以确定未知内力的大小和方向。
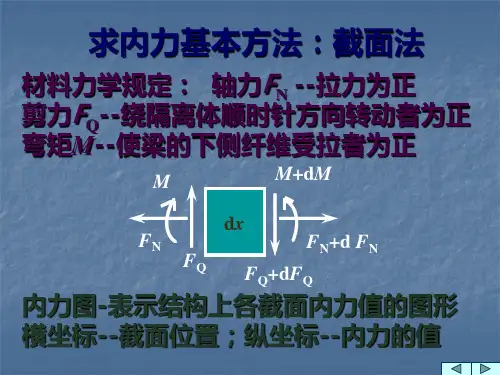

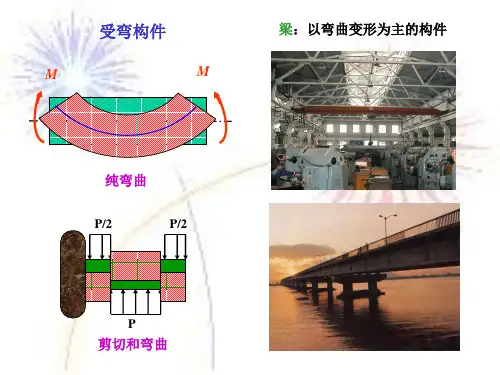


计算构件内力的基本方法一、构件内力的定义构件内力是指在构件内部产生的由外部作用力引起的内部力。
构件内力主要包括拉力、压力、剪力和弯矩等。
它们的作用是平衡外部作用力,使构件保持稳定。
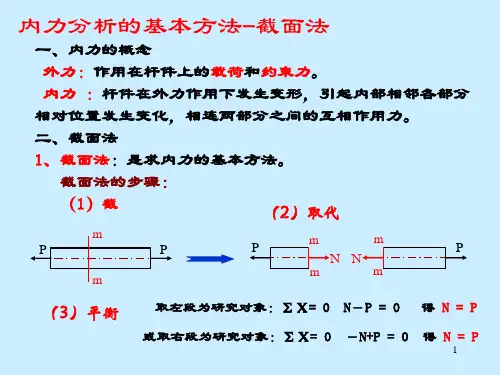
1. 自由体法:将构件从整体中分离出来,将其视为一个孤立的自由体,通过绘制受力图,可以得到构件上各点的受力情况。
利用平衡方程可以计算出构件内力的大小和方向。
2. 截面法:在构件的截面上选择一个点,通过分析该点的受力平衡条件,可以计算出该点的内力大小和方向。
截面法常用于计算梁、柱等构件的内力。
3. 变形法:根据构件的变形情况,通过应变与应力之间的关系,计算出构件内部的应力分布情况,从而计算出构件内力的大小和方向。
变形法常用于计算弹性构件的内力。
三、应用场景计算构件内力的基本方法适用于各种工程和力学问题。
例如,在建筑工程中,我们可以通过计算构件内力来确定柱子、梁、桁架等结构的强度和稳定性。
在机械工程中,我们可以通过计算构件内力来分析机械结构的受力情况,以确保其正常运行。
四、注意事项在计算构件内力时,需要注意以下几点:1. 确定坐标系:选择合适的坐标系可以简化计算过程,提高计算效率。
2. 合理假设:在实际计算中,为了简化问题,常常需要进行一些假设。
但是,假设应尽量符合实际情况,以保证计算结果的准确性。
3. 保持一致性:在计算过程中,应保持受力方向的一致性,以确保计算结果的正确性。
4. 考虑边界条件:边界条件对构件内力的计算有重要影响,需要在计算过程中充分考虑。
总结:计算构件内力是解决工程和力学问题的基础,掌握计算构件内力的基本方法对于工程师和研究人员来说至关重要。
通过自由体法、截面法和变形法等方法,可以准确计算出构件内力的大小和方向。
在应用过程中,需要注意选择合适的坐标系、合理假设、保持一致性和考虑边界条件,以确保计算结果的准确性。
希望本文对读者有所帮助,能够更好地理解和应用计算构件内力的基本方法。

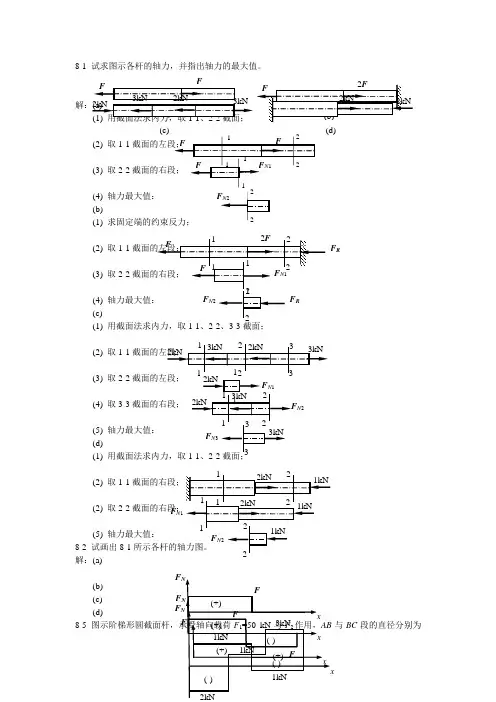
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。

8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2(4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5 图示阶梯形圆截面杆,段的直径分别为d 1=20(c) (d)F RN 2F N 3 F N 1 F NF N F Nmm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1)(2) 求1-1、2-28-6 题8-5d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1) 用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2)取[F ]= kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC的轴向变形△l 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
简述截面法求内力的过程
截面法是一种静力学方法,用于计算和分析结构中各个截面的内力。
其具体求解过程如下:
(1)根据结构的载荷情况和几何形状,选取一个截面。
(2)将该截面割开,同时保留截面两侧的支反力和弯矩。
(3)根据平衡条件和材料力学原理,分别求解在两侧支反力和弯矩的作用下,该截面两侧的内力分布。
(4)将所求的内力分布和所割开的截面形状结合起来,得到该截面中各点的内力大小和方向。
(5)重复上述过程,依次计算得到结构中各个截面的内力分布。
通过截面法求得的内力可以用于评估结构的受力性能、确定结构设计的可行性,以及优化结构的设计方案。