下载文档原格式
第2课时 平面直角坐标系中的位似变换1.理解位似图形的坐标变化规律；（难点）2.能熟练在坐标系中根据坐标的变化规律作出位似图形.（重点）一、情景导入观察如图所示的坐标系中的几个图形，它们之间有什么联系？二、合作探究 探究点：平面直角坐标系中的位似变换 【类型一】 求在坐标系中进行位似变化对应点的坐标在平面直角坐标系中，已知点A（6，4），B （4，－2），以原点O 为位似中心，相似比为12，把△ABO 缩小，则点A 的对应点A ′的坐标是（ ）A.（3，2）B.（12，8）C.（12，8）或（－12，－8）D.（3，2）或（－3，－2）解析：根据题意画出相应的图形，找出点A 的对应点A ′的坐标即可.如图，△A ′B ′O 与△A ″B ″O 即为所作的位似图形，可求得点A 的对应点的坐标为（3，2）或（－3，－2）.故选D. 方法总结：位似图形与位似中心有两种情况：（1）位似图形在位似中心两侧；（2）位似图形在位似中心同侧.若题中未指明位置关系，应该分两种情况讨论，防止漏解.【类型二】 在平面直角坐标系中画位似图形如图，在平面直角坐标系中，A （1，2），B （2，4），C （4，5），D （3，1）围成四边形ABCD ，作出一个四边形ABCD 的位似图形，使得新图形与原图形对应线段的比为2：1，位似中心是坐标原点.解析：以坐标原点O 为位似中心的两个位似图形，一种可能是位似图形在位似中心同侧，此时各顶点的坐标比为2；另一种可能是位似图形在位似中心的两侧，此时各顶点的坐标比为－2，此题作出一个即可.解：如图，利用位似变换中对应点的坐标的变化规律，分别取A′（2，4），B′（4，8），C′（8，10），D′（6，2），顺次连接A′B′，B′C′，C′D′，D′A′.则四边形A′B′C′D′就是四边形ABCD的一个位似图形.方法总结：画以原点为位似中心的位似图形的方法：将一个多边形各点的横坐标与纵坐标都乘±k（或除以±k），可得新多边形各顶点的坐标，描出这些点并顺次连接这些点即可.三、板书设计平面直角坐标系中的位似变换：在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k（k≠0），所对应的图形与原图形位似，位似中心是坐标原点，它们的相似比为|k|.位似变换是特殊的相似变换.以学生的自主探究为主线，培养学生的探索精神和合作意识.注重数形思想的渗透，通过坐标变换，在平面坐标系中，让学生画图、观察、归纳、交流，得出结论.在学习和探讨的过程中，体验特殊到一般的认知规律.通过交流合作，体验到成功的喜悦，树立学好数学的自信心.。
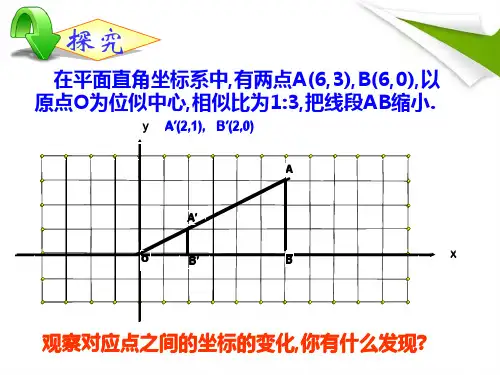
4.8.2 坐标中的位似关系学习目标：1. 知道位似图形在平面直角坐标系中的应用；2. 会根据相似比，求位似图形的顶点，以及根据位似图形对应点的坐标，求位似图形的相似比和在平面直角坐标系上作出位似图形．学习过程：预习导学阅读教材P115～117，自学“做一做”与“例2”，完成下列内容：(一)知识探究在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k ≠0)，所对应的图形与原图形________，位似中心是________，它们的相似比为________．(二)自学反馈(1)如图，在平面直角坐标系中，有两点A(6，3)、B(6，0)，以原点O 为位似中心，相似比为13，把线段AB 缩小，观察对应点之间坐标的变化，你有什么发现？(2)在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点坐标的比为________．(3)△ABC 和△A 1B 1C 1关于原点位似且点A(－3，4)，它的对应点A 1(6，－8)，则△ABC 和△A 1B 1C 1的相似比是________．(4)已知△ABC 三顶点的坐标分别为A(1，2)，B(1，0)，C(3，3)，以原点O 为位似中心，相似比为2，把△ABC 放大得到其位似图形△A 1B 1C 1，则△A 1B 1C 1各顶点的坐标分别为A 1______________，B 1______________，C 1______________.合作探究活动1 小组讨论例1.如图，在平面直角坐标系中，△OAB 三个顶点的坐标分别是O （0,0），A （3,0），B （2,3）.（1）将点O,A,B 的横坐标、纵坐标都乘2，得到三个点，以这三个点为顶点的三角形与△OAB 位似吗？如果位似，指出位似中心和相似比.（2）如果将点O,A,B 的横坐标、纵坐标都乘-2呢？例2.如图，在平面直角坐标系中，四边形ABCD 的顶点坐标分别是A （4, 2），B （8,6），C （6,10），D （-2,6）.（1）将点A,B,C,D 的横坐标、纵坐标都乘以12，得到四个点，以这四个点为顶点的四边形与四边形ABCD 位似吗？如果位似，指出位似中心和相似比.（2）如果将点A, B, C, D 的横坐标、纵坐标都乘12呢？例3.在平面直角坐标系中，四边形OABC 的顶点坐标分别是O （0，0），A （6,0），B （3,6），C （-3，3）.以原点为位似中心，画一个四边形，使它与四边形OABC 位似，且相似比是2:3.活动2 跟踪训练1．某个图形上各点的横、纵坐标都变成原来的12，连接各点所得的图形与原图形相比( ) A ．完全没有变化 B ．扩大成原来的2倍C ．面积缩小为原来的14D ．关于纵轴成轴对称 2．如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值( )A ．只有1个B ．可以有2个C ．有2个以上但有限D ．有无数个3．在平面直角坐标系中，将坐标为(0，0)、(2，4)、(2，0)、(4，4)、(6，0)的点用线段顺次连接起来形成一个图案．(1)将这五个点的纵坐标不变，横坐标变为原来的13，求上述点的坐标，将所得的五个点用线段顺次连接起来，所得图案与原图案相比有什么变化？(2)横坐标不变，纵坐标分别减去3呢？(3)横坐标都加上3，纵坐标不变呢？(4)横、纵坐标都乘以－1呢？(5)横、纵坐标分别变成原来的2倍呢？面积如何变化？活动3 课堂小结课后检测1.如图，在平面直角坐标系中，以原点O 为位似中心，用上一课的方法画出五边形OBCDE 的位似图形，使它与五边形OBCDE 的相似比为1:2，比较两个图形对应点的坐标，你能发现那么？。
第2课时 坐标系中的位似图形
要点感知 一个多边形的顶点坐标分别扩大或缩小相同的倍数，所得的图形与原图形是以
为位似中心的位似图形.在平面直角坐标系中，如果位似是以原点为位似中心，位似比为k ，那么位似图形对应点的坐标的比等于 或 .
预习练习1-1 (2019·孝感)在平面直角坐标系中，已知点E(-4，2)，F(-2，-2)，以原点O 为位似中心，相似比为12，把△EFO 缩小，则点E 的对应点E ′的坐标是( )
A.(-2，1)
B.(-8，4)
C.(-8，4)或(8，-4)
D.(-2，1)或(2，-1)
1-2 如图，已知O 是坐标原点，△OBC 与△ODE 是以O 点为位似中心的位似图形，且△OBC 与△ODE 的相似比为1∶2，如果△OBC 内部一点M 的坐标为(x ，y)，则M 在△ODE 中的对应点M ′的坐标为( )
A.(-x ，-y)
B.(-2x ，-2y)
C.(-2x ，2y)
D.(2x ，-2y)
1-3 △ABC 和△A ′B ′C ′关于原点位似，且点A(-3，4)，它的对应点A ′(6，-8)，则△ABC 与△A ′B ′C ′的相似比是 .
知识点 以坐标原点为位似中心的位似图形的坐标变化规律
1.(2019·青岛)如图，△ABO 缩小后变为△A ′B ′O ，其中A ，B 的对应点分别为A ′，B ′点A ，B ，A ′，B ′均在图中在格点上.若线段AB 上有一点P(m ，n)，则点P 在A ′B ′上的对应点P ′的坐标为( )
A.(2m ，n)
B.(m ，n)
C.(m ，2n )
D.(2m ，2
n )
2.如图，原点O 是△ABC 和△A ′B ′C ′的位似中心，点A(1，0)与点A ′(-2，0)是对应点，点B(2，2)，则B ′点的坐标 .
3.如图，在平面直角坐标系中，△ABC 和△A ′B ′C ′是以坐标原点O 为位似中心的位似图形，且点B(3，1)，B ′(6，
2).
(1)若点A(52
，3)，则A ′的坐标为 ；
(2)若△ABC的面积为m，则△A′B′C′的面积= .
4.如图，△OAB三个顶点的坐标分别为O(0，0)，A(1，2)，B(3，0).以O为位似中心，画出一个△OA′B′，使得△OA′B′与△OAB的相似比为2∶1，并写出点A′和点B′的坐标.
5.如图，已知O是坐标原点，B，C两点的坐标分别为(3，-1)，(2，1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2），画出图形；
(2)分别写出B，C两点的对应点B′，C′的坐标.
6.(2019·毕节)如图，在平面直角坐标系中，以原点O为位似中心，将△ABO扩大到原来的2倍，得到△A′B′O.若点A的坐标是(1，2)，则点A′的坐标是( )
A.(2，4)
B.(-1，-2)
C.(-2，-4)
D.(-2，-1)
7.如图，已知点E(-4，2)，点F(-1，-1)，以O为位似中心，把△EFO放大为原来的2倍，则E点的对应点坐标为( )
A.(2，-1)或(-2，1)
B.(8，-4)或(-8，4)
C.(2，-1)
D.(8，-4)
8.某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a，b)对应大鱼上的点( )
A.(-2a，-2b)
B.(-a，-2b)
C.(-2b，-2a)
D.(-2a，-b)
9.如图，△ABC缩小后得到△A′B′C′，则△ABC与△A′B′C′的位似比为.
10.已知△ABC位于平面直角坐标系内如图.
(1)将△ABC各顶点的坐标分别乘以-2，作为点A1，B1，C1的坐标，画出△A1B1C1；
(2)试说明△A 1B 1C 1与△ABC 有什么关系？
11.已知△ABC 的三个顶点坐标如下表：
(1)将下表补充完整，并在直角坐标系中，画出△A ′B ′C ′；
(2)观察△ABC 与△A ′B ′C ′，写出有关这两个三角形关系的一个正确结论.
挑战自我
12.已知，△DEF 是△ABC 的位似三角形(点D ，E ，F 分别对应点A ，B ，C)，原点O 为位似中心，△DEF 与△ABC 的位似比为k.
(1)若位似比k=12
，请你在平面直角坐标系的第四象限中画出△DEF ； (2)若位似比k=m ，△ABC 的周长为C ，则△DEF 的周长= ；
(3)若位似比k=n ，△ABC 的面积为S ，则△DEF 的面积= .
参考答案
课前预习
要点感知 坐标原点 k -k
预习练习1-1 D 1-2 B 1-3 1∶2
当堂训练
1.D
2.(-4，-4)
3.(1)(5，6)(2)4m
4.图略：A′(2，4)，B′(6，0).
5.(1)图略.
(2)B′的坐标是(-6，2)，C′的坐标是(-4，-2).
课后作业
6.C
7.B
8.A 9 .3∶1
10.(1)图略.
(2)△A1B1C1与△ABC以原点O为位似中心的位似图形，位似比为2.
11.(1) 8 6 10 2 ；
(2)△A′B′C′是△ABC放大2倍的位似图形.也可写出有关两三角形形状、大小、位置等关系，如△ABC∽△A′B′C′、周长比、相似比、位似比等.
12.(1)图略.
(2)∵位似比k=m，△ABC的周长为C，∴△DEF的周长=mC.
(3)∵位似比k=n，△ABC的面积为S，∴△DEF的面积=n2S.。
