平面直角坐标系中的位似.ppt

格式：ppt
大小：2.45 MB
文档页数：17

下载文档原格式

《位似》相似PPT课件3

y
A
D
A′
B
D′
B′
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他(qítā)办法吗?试试看.
第二十七页，共32页。
x
第二十七页，编辑(biānjí)于星期五：十五点十四分。
练一练:
1.如图表示△AOB和把它缩小(suōxiǎo)后得到的△COD,求它们的相似比
练一练:
3.如图,已知矩形(jǔxíng)wxyz各点的坐标,如果矩形( jǔxíng)STUV相似于wxyz 点S 的坐标为(2,2),按照下列相似比,分别写出T、U、V各点的坐标.
(1)相似比为 12;
y
z ( 1,4 )
y ( 5,4 )
S ( 2,2 )
W ( 1,1 )
x ( 5,1 )
第十五页，共32页。
第十五页，编辑(biānjí)于星期五：十五点十四分。
A
O
B C
第十六页，共32页。
第十六页，编辑(biānjí)于星期五：十五点十四分。
A
以0为中心把△ABC B
缩小为原来(yuánlái)的一半。
C
O C’
B’
A’
第十七页，共32页。
第十七页，编辑(biānjí)于星期五：十五点十四分。
为位似中心,相似比为2画它的位似图形.
放大后对应点的坐标(zuòbiāo)分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4
A
3
2
B'
1

九年级数学上册知识点---- 平面直角坐标系中的位似变换

归纳：
1. 在平面直角坐标系中，以原点为位似中心作一个图形的位似图形可以作两个．
2. 当位似图形在原点同侧时，其对应顶点的坐标的比为 k；当位似图形在原点两侧时，其对应顶点的坐标的比为－k．
3. 当 k＞1 时，图形扩大为原来的 k 倍；当 0＜k＜1 时，图形缩小为原来的 k 倍．
练一练
可以确定其他顶点的坐标.
自己试一试.
解：利用位似中对应点的坐标的变化规律，分别取点 A′ (－3，6)，B′ (－3，0)，O (0，0). 顺次连接点 A′ ，B′ ，O，所得的 △A′ B′ O 就是要画的一个图形.
练一练在平面直角坐标系中，四边形 OABC 的顶点坐标
分别为 O (0，0)，A (6，0)，B (3，6)，C (－3，3). 以原点 O 为位似中心，画出四边形 OABC 的位似图形，使它与四边形 OABC 的相似是 2 : 3.
标都乘 2 ；在平面 3
4 C
2
直角坐标系中描点
A″
A
O (0，0)，A″ (－4，－4 0)，B″ (－2，－4)， C″ (2，－2)，用线段顺次连接O，A″，
O －2
B″ －4
6x 4 C″
B″，C″.
平面直角坐标系中的图形变换
至此，我们已经学习了四种变换：平移、轴对称、旋转和位似，你能说出它们之间的异同吗？在右图所示的图案中，你能找到这些变换吗？
B" (－2 ，0 ).

2. △ABC 三个顶点坐标分别为 A (2，3)，B (2，1)，
C (5，2)，以点 O 为位似中心，相似比为 2，将
△ABC 放大，观察对应顶点坐标的变化.
y 6

《位似》相似(第2课时平面直角坐标系中的位似)

结合相似判断
在平面直角坐标系中，如果两个图形相似，则它们一定位似；反之，如果两个图形位似，不一定相似。
03
位似在实际生活中的应用
在艺术和设计中的应用
01
缩放和变形
在艺术和设计中，位似可以将图像进行缩放和变形，从而创造出不同
的视觉效果。例如，在制作电影特效或动画时，可以使用位似来改变
角色的形状或大小。
引入本课时的学习目标
总结词：介绍
详细描述：通过展示图片、实例和问题，引导学生了解本课时要学习的内容，明确学习目标和重点难点，激发学生的学习兴趣和积极性。
02
平面直角坐标系中的位似
定义位似中心和位似比
定义位似中心
在平面直角坐标系中，选择一个点作为位似中心，通常选择原点或对称中心。
定义位似比
位似比是位似图形与原图形之间的相似比，表示为k，其中 k>0。
利用位似知识解决实际问题
总结词
在实际问题中，经常会遇到与位似相关的应用，如利用位似设计图案、放大或缩小物体等。解决这类问题时，需要根据实际情况建立适当的数学模型，然后利用位似知识进行求解。
详细描述
在实际问题中，位似知识可以应用于许多方面，如建筑设计、图案设计、放大或缩小物体等。为了解决这些问题，我们需要根据实际情况建立适当的数学模型，将实际问题转化为数学问题。然后利用位似知识求解，得到我们需要的答案。在建立数学模型时，需要注意变量的选择和单位的统一，以确保计算结果的正确性和可比较性。
总结词
详细描述
理解位似概念
学生需要判断两个图形是否位似，并说明理由。这有助于巩固学生对位似概念的理解，
了解位似的定义和判断方法。
提高题：探究位似在解决实际问题中的应用

《平面直角坐标系中的位似变换》PPT课件

11．在平面直角坐标系中，将坐标是(0，4)，(1，0)，(2，4)， (3，0)，(4，4)的点用线段依次连接起来形成一个图案．
(1)在如图所示的坐标系中画出这个图案 (图案①)．解：图略．
(2)若将上述各点的横坐标保持不变，纵坐标分别乘－1，再将所得的各点用线段依次连接起来，画出所得的图案 (图案②)．解：将点(0，4)，(1，0)，(2，4)，(3，0)，(4，4)的横坐标保持不变，纵坐标分别乘－1，得(0，－4)，(1，0)， (2，－4)，(3，0)，(4，－4)，然后描点连线，图略．
教师课堂用语在学科专业方面重在进行“引”与“导”，通过点拨、搭桥等方式让学生豁然开朗，得出结论，而不是和盘托出，灌输告知。一般可分为：启发类、赏识类、表扬类、提醒类、劝诫类、鼓励类、反思类。
一、启发类
1. 集体力量是强大的，你们小组合作了吗?你能将这个原理应用于生活吗?你的探究目标制定好了吗? 2. 自学结束，请带着疑问与同伴交流。 3. 学习要善于观察，你从这道题中获取了哪些信息? 4. 请把你的想法与同伴交流一下，好吗? 5. 你说的办法很好，还有其他办法吗?看谁想出的解法多? 二、赏识类
后的图形△A2B2C；如图，△A2B2C就是所要画的三角形．
(3)在(2)的条件下求出点B经过的路径长．
解：CB＝ 12＋42＝ 17，
点 B 经过的路径长为14×2π×
17＝
17 2 π.
10．【中考·眉山】如图，已知△ABC的三个顶点的坐标分别为 A(0，－3)，B(3，－2)，C(2，－4)．(正方形网格中，每个小正方形的边长是1个单位长度)
答案显示
1．【中考·辽阳】如图，在由边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点(网格线的交点)上，则点P的坐标为( C )

时平面直角坐标系中的位似课件

关系
位似变换与坐标系之间存在密切关系。一方面，通过位似变换可以改变点的坐标，从而改变图形的大小、形状和位置；另一方面，坐标系本身也是一种特殊的位似变换，即平移和伸缩变换。因此，通过研究位似变换和坐标系之间的关系，可以更好地理解图形的性质和规律。
相似三角形与位似图形的联系
相似三角形
如果两个三角形对应角相等，对应边成比例，那么这两个三角形
时平面直角坐标系中的位似课件
• 位似在平面直角坐标系中的应用
定义与性质
位似定义位似性质
图形相似与位似
图形相似
位似与相似关系
位似变换是相似变换的一种特殊形式，即当相似比为1时，就得到了位似变换。
位似与距离关系
点与点之间的距离变化距离比例关系平行线之间的距离变化
平移、旋转及位似的变换关系
应用
图形位似变换被广泛应用于图形的测量、设计和分析中。例如，可以通过位似变换来缩放和翻转一个图形，以便进行测量和设计；也可以通过对图形进行位似变换来研究图形的性质和规律。
位似与坐标系的关系
定义
在平面直角坐标系中，位似变换可以用相似矩阵来表示。相似矩阵是保持点坐标的形状和大小关系的矩阵，其元素是实数。
平移变换
旋转变换
位似变换
位似与平移、旋转的综合应用
位似与平移的综合应用
位似与旋转的综合应用
位似在几何作图中的应用
利用位似进行几何作图
位似作图的实际应用
点的位似变换
01
定义
02
分类
03
性质
图形位似变换的应用
定义
图形位似变换是指将一个图形通过位似变换得到另一个图形，通过对另一个图形的操作来研究原图形的性质和规律。

平面直角坐标系中的位似变换课件

B′(4,3)
2 A′(2,1) A
-4 -2A′O′(-2,-1)2 4 6 8
x
-2
D′′(1,-3) B′′(-4,-3) -4
C′′(-3,-5)-6
例在平面直角坐标系中，四边形 OABC的顶点坐标分别是 O(0,0) ， A(6,0) ， B(3,6)，C(-3,3).以原点O为位似中心画一个四边形， -6 使它与四边形 OABC位似，且类似比是2∶3.
x 6 4 2
-6 -4
-2 O -2
-4
-6
B′ B
（1）将点O，A，B的横、纵坐标都
乘2，得到O′（ 0,0），A′（ 6,0）， B′（ 4,6）
A 24
（2） △OAB和△OA′B′是位似的，
A′ 6
y 位似中心是点O，类似比是2.
在直角坐标系中，△OAB三个顶点的坐标分别为O（0，0）， A（3，0），B（2，3）.
A′ -6 -4
2 -2 O
（2） △OAB和△OA′B′是位似的，
Байду номын сангаас
A 24
6
y 位似中心是点O，类似比是-2.
-2
-4
-6 B′
探究新知
y C
10
在直角坐标系中，四边形
8
OABC的顶点坐标分别为A(4,2)， D 6 C′(3,5)
B
B(8,6)，C(6,10)， D(-2,6).将点
O，A，B，C的横、纵坐标都
x 6 4 C 2
-4 -2 O -2 -4
-6
B
A 24 6y
四边形OABC的顶点坐标都乘 2 分别是O(0,0)，

《位似》相似PPT(第1课时位似图形的概念及画法)

似中心的位似图形，且

′
＝

＝
′
′
＝

′
；五边形ABCDE 与五

边形A′ B′ C′ D′ E′是以点O 为位似中心的位似图形，且′ ＝ ′ ＝

′

＝ ′ ＝ ′ .
例1 请指出下列图形那些是位似图形？并指出位似图形图的位似中心?
所示）.
课堂小结
两个相似多边形，如果它们对应顶点所在的直线相交于
定义
一点，并且这点与对应顶点所连线段成比例,我们就把这
样的两个图形叫做位似图形，这个交点叫做位似中心．
① 两个图形相似.
位似图形的概念
及画法
性质
②对应点的连线相交于一点，对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
英语课件：/keji an/ying yu/
科学课件：/keji an/kexue/
化学课件：/keji an/huaxue/
地理课件：/keji an/dili/
2
PPT素材：/s ucai/
其与△ABC位似，且位似比为2.
D
解：画射线OA、OB、OC；
在射线OA、OB、OC上分别取点D、E、F，
使OD = 2OA，OE = 2OB，OF = 2OC；
A
E
顺次连结D、E、F,使△DEF与△ABC位似，
B
相似比为2.
想一想：你还有其他的画法吗？
O
C
F
思考：上面点 O取在两个三角形的同侧，如果点 O在两
知识讲解
★
位似图形的概念
问题：下面两个多边形相似，将两个图形的顶点

位似(第2课时)平面直角坐标系中的位似-2021-2022学年九年级数学下册同步课件(人教版)

OABC 各顶点的坐标都乘 2 ；在平面直角坐标
3 系中描点O (0，0)，
A' (4，0)，B' (2，4)，
C′ (－2，2)，用线段顺
次连接O，A'，B'，C'.
y 6
4 C
C' 2
－4
O
－2
－4
B B'
A' A 6x
4
画法二：将四边形 OABC 各顶点的坐标都乘 Hale Waihona Puke ；3 在平面直角坐标系中描点
新知探究
一、平面直角坐标系中的位似变换
在平面直角坐标系中，有两点A(6，3)，B(6，0)，以原点O为位似中心，
相似比为 1，把线段AB缩小.
3
y
A
(2,1) A'
O B' (2,0)
B
x
观察对应点的坐标变化，发现横纵坐标均是原来的
1 3
.
在平面直角坐标系中，有两点A(6，3)，B(6，0)，以原点O为位似中心，
【解答】解：∵B（0，1），D（0，3）． ∴OB=1，OD=3． ∵△OAB以原点O为位似中心放大后得到△OCD． ∴△OAB与△OCD的相似比是OB：OD=1:3．故选：D．
感受中考
2.（4分）（2020•重庆A卷8/26）如图，在平面直角坐标系中，△ABC的顶点坐标
分别是A（1，2），B（1，1），C（3，1），以原点为位似中心，在原点的同侧
2
纵坐标： 4 3 6
2
A(3,6)
A′
y
6
A4
2
B′ B
B′′
－4 －2 O 2
x
同理可得Bꞌꞌ(3，0)，O(0，0)

位似--课件

-6
-8
B"
2. 如图，△ABC三个顶点坐标分别为A（2，－
2），B（4，－5），C C"
（5，－2），以原点O为
8 6
A" 4
2
位似中心，将这个三角形放大为原来的2倍．
-12 -10-9-8 -6 -4
-2 O 2 4 6
-2 A
C
-4 A'
-6
B
8 9 101112
C'
-8
解：
B'
A'（ 4 ，－ 4 ），B ' （ 8 ，－ 10 ），C ' （ 10 ，－4 ），
（1）从上面练习第 1(1)(4)题图中，我们可以看到，△OAB∽△O A′B′,
则 OA OA′
＝ OB OB′
＝ AB A′B′
.从第
2
题的图中同样可以看到AADF
＝AACP
＝AAEB ＝BECP ＝DFPC
一般地，位似图形有以下性质：位似图形上任意一对对应点到位似中心的距离之
比等于位似比.
是（2）在平行四边形ABCD中，△ABO与 △CDO
是
不是
练一练：判断下列各对图形哪些是位似图形，哪些不是. （3）正方形ABCD与正方形A′B′C′D′. （4）等边三角形ABC与等边三角形A′B′C′
是
是
练一练：判断下列各对图形哪些是位似图形，哪些不是.
（5）反比例函数 y＝6x （x>0）的图像与 y＝x6 （x<0）的图像（6）扇形ABC与扇形A′B′C′，
在日常生活中，我们经常见到这样一类相似的图形，例如，放映幻灯时，通过光源，把幻灯片上的图形放大到屏幕上（如图显示了它工作的原理）．在照相馆中，摄影师通过照相机，把人物的形象缩小在底片上．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例.如图，请以坐标原点O为位似中心，作平行四边形ABCD的位似图形，并把它的边长放大 2 倍 . Y 分析：根据位似图形上任意一对对应点到位似中心的距离之比等于位似比，我们只要连结位似 -12 -10 中心O和的各顶点，并把线段延长（或反向延长）到原来的2倍，就得到所求作图形的各个顶点
8 6 4 2
-10 -8 -6 -4 -2
A
D
X
0
-2 -4 -6 -8
B2 4 6C 8
10
-10
3．如图，在直角坐标系中，△ABC 的各个顶点的坐标为 A （－1，1），B（2，3），C（0，3）.现要以坐标原点 O 为位似 2 中心，位似比为，作△ABC 的位似图形△A′B′C′，则它 3 的顶点 A′、B′、C′的坐标各是多少？
若原图形上点的坐标为（x，y），像与原图形的位似比为k，则像上的对应点的坐
标为（kx，ky）或（―kx，―ky）.
练一练: 1.如图表示△ABC把它缩小后得到的
△COD,求它们的相似比
y
A
C
x o
D B
练一练: 2.如图△ABC的三个顶点坐标分别为
A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
A
A'
x o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1),B′(2,0)
A
A〞(-2,-1),B(-2,0)
A'
B〞
x o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
E B O D F E
C
A
F D O
C A B
位似中心对应点连线都交于____________ 平行或在一条直线上对应线段_______________________________
探索1:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小. y A′(2,1), B′(2,0)
y o
A C
x
B
练一练:
3.如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,7),按照下列相似比,分别写出T、U、V各点的坐标.
(1)相似比为4;
y z
1 (2)相似比为 2 ;
y
W
o
x
x
10 Y
如图,请以坐标原点O为位似中心，作平行四边形的位似图形，并把它的边长放大３倍．
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标
分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形. y
至此,我们己经学习了四种变换;平移轴、对称、旋转和位似,你能说出它们之间的异同吗?在图所示的图案中,你能找到这些变换吗?
• 不经历风雨，怎么见彩虹 • 没有人能随随便便成功!
12
10 8 6 4
G
F
A D B
C
4 6 8
E′
-8 -6
C′
-4 -2
2
0 -2 -4 2
E
10 12
X
-6
F′
-8
-10
-12
G′
想一想： 1．四边形GCEF与四边形G′C′E′F′具有怎样的对称性？ 2．怎样运用像与原像对应点的坐标关系，画出以原点为位似中心的位似图形？
以坐标原点为位似中心的位似变换有一下性质：
复习回顾
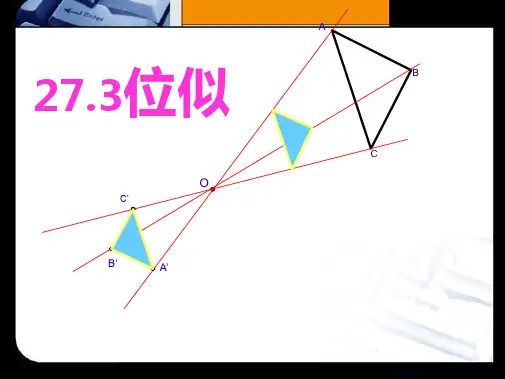
1.什么叫位似图形? 如果两个图形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形, 这个点叫做位似中心, 这时的相似比又称为位似比.
2.位似图形的性质
位似图形上的任意一对对应点到位似中心的距离之比等于位似比 3.利用位似可以把一个图形放大或缩小
复习回顾
如何把三角形ABC放大为原来的2倍?
A
D
A′
B
D′ B′
x
C′
C
o
A′( -3,3 -1,2 ) 你还有其他办法吗?试试看.
课堂小结一、定义及性质：二、位似图形的画法： 1、画出基本图形 2、选取位似中心 3、根据条件确定对应点，并描出对应点 4、顺次连结各对应点，所成的图形就是所求的图形三、位似变换与坐标的关系：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k