半导体物理第3次课

教科版高三物理选修3《半导体》教案及教学反思教学目标1.了解半导体元器件的种类、特性及应用；2.学习 pn 结的工作原理及特性；3.熟悉二极管、三极管的结构、特性及应用；4.掌握半导体场效应管和光电导的基本原理；5.了解半导体器件的发展现状。

教材分析本单元主要内容是半导体器件。

在教学中，我们主要采用教科版高中物理选修3中的相关章节进行讲解。

该章节主要包括以下内容：1.半导体器件的种类和特性；2.pn 结的工作原理和特性；3.二极管、三极管的结构、特性和应用；4.半导体场效应管的基本原理；5.光电导的基本原理；6.半导体器件的发展现状。

教学步骤第一步：半导体器件的种类和特性通过演示一些半导体元器件的实物及用途，让学生了解半导体器件的种类和特性，掌握半导体原理。

重点关注半导体器件在电子产品中的应用。

第二步：pn 结的工作原理和特性为了帮助学生更好地理解 pn 结的原理和特性，我们将设置和演示一些模拟实验，让学生亲自体验 pn 结的电性质并掌握其工作原理。

第三步：二极管、三极管的结构、特性和应用通过对不同类型二极管、三极管的演示及其内部结构的说明，让学生掌握二极管、三极管的原理，了解其特性及应用。

进一步，演示一些简单电路供学生模拟操作。

第四步：半导体场效应管的基本原理讲解半导体场效应管的原理及其内部结构，让学生了解其特性，以及场效应管的应用，引导学生对场效应管的性质及应用深入理解，并通过简单电路模拟进行实践操作。

第五步：光电导的基本原理通过简短的理论讲解和实验实际操作进行演示，让学生了解光电导的基本原理及其应用于光电传输、光电显示、光电控制等领域的重要性。

第六步：半导体器件的发展现状在本单元的最后一个阶段，我们将介绍当前半导体器件的发展现状，即对当前半导体器件发展趋势、发展瓶颈和发展前景进行详细描述，供学生进行思考和交流，进一步加深对半导体器件的认识和理解，促进学生的主动学习。

教学反思本单元的教学以理论课程、实验教学、模拟电路操作为主，采用讲解、演示、交流的多种方式。

2. 半导体-教科版选修3-3教案一、教育背景本教案适用于教育部教科版选修3-3中的半导体章节。

该章节主要介绍半导体物理学知识，包括半导体的基本概念、半导体材料的物理性质、半导体元器件的基本构造和工作原理等。

二、教学目标1.了解半导体基本概念。

2.知道半导体物理性质。

3.掌握半导体元器件基本构造和工作原理。

4.掌握符号表示和实际电路应用。

三、教学内容3.1 半导体的基本概念1.半导体的基本定义2.导体、半导体、绝缘体的区别3.拉曼散射和荧光光谱的测量结果4.半导体的主要应用3.2 半导体材料的物理性质1.半导体材料的物理性质2.材料的能带结构3.杂质掺杂4.pn结的形成及其特点3.3 半导体元器件的基本构造和工作原理1.半导体二极管的基本构造和工作原理2.它的符号表示和实际电路应用3.内置式二极管4.可变电容二极管3.4 半导体三极管和场效应管1.半导体三极管的基本构造和工作原理2.它的符号表示和实际电路应用3.常用的三极管型号及其参数4.场效应管的基本构造和工作原理5.它的符号表示和实际电路应用四、教学方法通过理论授课和实验操作相结合的方式，加深学生对半导体物理知识的理解。

在授课过程中可以带上相关实验，通过实验现象让学生更好地理解半导体元器件的基本构造和工作原理。

五、实验设计1.接线实验：让学生对半导体二极管进行基本接线实验，观察输出波形及稳压效果等。

2.排序实验：让学生对常用的三极管型号及其参数进行排序，了解不同型号三极管的特点。

3.可编程场效应管实验：让学生掌握场效应管的基本构造和工作原理。

六、教学成果评估通过期末考试、平时作业和实验表现来评估学生掌握半导体物理知识的程度。

七、教学注意事项1.教学过程中一定要注重学生的实际操作。

2.实验安全第一，学生必须遵守实验室安全规定。

3.实验装置要一一对照，仔细查验，发现缺陷要及时处理。

八、教学参考资料1.《半导体物理学》（叶生平、高书荣编著）2.《半导体器件基础》（洪承德等编著）3.《数字电路与半导体器件》（张丽娟主编）。

第三章习题和答案1. 计算能量在E=E c 到2*n2C L2m 100E E π+= 之间单位体积中的量子态数。

解：2. 试证明实际硅、锗中导带底附近状态密度公式为式（3-6）。

322233*28100E 21233*22100E 0021233*231000L8100)(3222)(22)(1Z VZ Z )(Z )(22)(2322C22CLE m hE E E m V dEE E m V dEE g Vd dE E g d E E m V E g cn c C n lm h E C nlm E C nn c n c πππππ=+-=-====-=*++⎰⎰**）（）（单位体积内的量子态数）（)(21)(,)"(2)()(,)(,)()(2~.2'213''''''2'21'21'21'2222222C a a l t tz y x ac c zla z y ta yx ta xztyx C C e E E m hk Vm m m m k g k k k k k m hE k E k m m k k m m kk m m kmlk m k k hE k E K IC E G si -=⎪⎪⎭⎫ ⎝⎛+∙=+++====+++=*****系中的态密度在等能面仍为球形等能面系中在则：令）（关系为）（半导体的、证明：3. 当E-E F 为1.5k 0T ，4k 0T, 10k 0T 时，分别用费米分布函数和玻耳兹曼分布函数计算电子占据各该能级的概率。

费米能级费米函数玻尔兹曼分布函数1.5k 0T 0.182 0.223 4k 0T 0.018 0.018310k 0T4. 画出-78o C 、室温（27 o C ）、500 o C 三个温度下的费米分布函数曲线，并进行比较。

5. 利用表3-2中的m *n ，m *p 数值，计算硅、锗、砷化镓在室温下的N C , N V 以及本征载[]3123221232'2123231'2'''')()2(4)()(111100)()(24)(4)()(~ltn c n c lt t z m msm VE E hm E sg E g si VE E h m m m dE dzE g dkk k g Vk k g d k dE E E =-==∴-⎥⎥⎦⎤⎢⎢⎣⎡+∙∙==∴∙=∇∙=+**πππ）方向有四个，锗在（旋转椭球，个方向，有六个对称的导带底在对于即状态数。

第三章习题讲解7.Ec − E F 解： Q n0 = N c exp(− ) k0T∴ ∴ Q ∴ EF Nc = E c − k 0 T ln = E c − 0 . 017 eV n0E F − E c = − 0 . 017 eV E c − E D = 0 . 01 eV E F − E D = − 0 . 007 eVND n0 = 1 + 2 exp[( E F − ED ) / k0T ] ⇒ N D = 1.7 ×1017 cm −3ND 9. E F = Ec + k 0T ln Nc N D1 E F 1 = Ec + k 0T ln = Ec − 0.206eV Nc EF 2 EF 3 N D2 = Ec + k 0T ln = Ec − 0.087eV Nc N D3 = Ec + k 0T ln = Ec − 0.027eV NcEc − E D = 0.05eVEF1远在ED之下，故此时全电离方法1 方法2(Ec-EF2) /k0T=1.4,故此时不能全电离 EF3在ED之上，故此时全电离+ nD 1 = N D 1 + 2 exp[−( ED − EF ) / k 0T ]1 = 是否大于90％ 1 + 2 exp[−( Ec − ΔED − EF ) / k 0T ]算出电离度分别为1，67％，55％。

所以第二、三种 不能认为全电离。

10. 解：Ge 在300K时的本征载流子浓度ni = 2.4 × 10 cm13−3要以杂质电离为主，其杂质浓度最低应 高于ni一个数量级，即：N D ,min = 1014 cm −3最高浓度为：⎛ ΔE D ⎞ ⎛D N ⎞ N D = ⎜ − C ⎟ exp⎜ − ⎜ k T ⎟= ⎟ ⎝ 2 ⎠ 0 ⎝ ⎠ ⎛ 0.1 × 1.05 × 1019 ⎞ 0.0127 ⎞ 17 −3 ⎜ ⎟ exp⎛ − ⎟ = 3.22 × 10 cm ⎜ ⎜ ⎟ 2 ⎝ 0.026 ⎠ ⎝ ⎠11. 根据未电离杂质占总掺杂比例的定义：ΔE D 2N D ⇒ D− = exp Nc k 0T ⎡⎛ D ΔE D 1 3 = ln T + ln ⎢⎜ − ⎜ k0 T 2 ⎢⎝ N D ⎣∗ 3/ 2 k 0 mn 3⎞ 2π ⎟ ⎟ h ⎠(∗ 3/ 2 k 0 mn 3)(2π 其中)⎤ ⎥ ⎥ ⎦h＝1015ΔE D ＝116 k0将上两个常数代入，得 ： ⎛ D− 116 3 = ln T + ln ⎜ ⎜N T 2 ⎝ D ⎞ ⎟＋15 ln 10 ⎟ ⎠(1) 将N D＝1014 cm −3D−＝1 ％代入116 3 ⎛ 0.01 ⎞ = ln T + ln⎜ 14 ⎟＋15 ln 10 T 2 ⎝ 10 ⎠ 3 ＝ ln T－2.3 2 ⇒ T = 37.1K 将N D＝1017 cm −3 D−＝1 ％代入 116 3 ⎛ 0.01 ⎞ = ln T + ln⎜ 17 ⎟＋15 ln 10 T 2 ⎝ 10 ⎠ 3 ln T－9.2 2 ⇒ 533K(1) 将N D＝1014 cm −3D−＝10％代入116 3 3 ⎛ 0.1 ⎞ = ln T + ln⎜ 14 ⎟＋15 ln 10＝ ln T T 2 2 ⎝ 10 ⎠ ⇒ T = 24.3 将N D＝1017 cm −3 D−＝10％代入 116 3 ⎛ 0.1 ⎞ = ln T + ln⎜ 17 ⎟＋15 ln 10 T 2 ⎝ 10 ⎠ 3 ln T－6.9 2 ⇒ T = 160.5 K50%电离时，不能再用上方法，须用：ND ⎛ ED − EF 1 1 + exp⎜ ⎜ kT 2 0 ⎝⎞ ⎟ ⎟ ⎠ND = ⎛ EF − ED ⎞ 1 + 2 exp⎜ ⎜ kT ⎟ ⎟ 0 ⎝ ⎠⎛ EF − ED ⎞ ⎛ ED − EF ⎞ ⎟ ⎟ = 4 exp⎜ ⇒ exp⎜ ⎜ kT ⎟ ⎜ kT ⎟ 0 0 ⎠ ⎝ ⎠ ⎝ ED − EF EF − ED ⇒ = ln 4 + k 0T k 0T ⇒ E F = E D − k 0T ln 2 (1)⎛ E F − Ec ⎞ ND n0 = = N c exp⎜ ⎟ ⎜ kT ⎟ 2 0 ⎠ ⎝ ⎛ ND ⎞ ⇒ E F = Ec + k 0T ln⎜ ⎟ ⎜ 2N ⎟ c ⎠ ⎝ ( 2)联立（1）、（2）两式可得：⎛ ND ⎞ ⎟ E D − k 0T ln 2 = Ec + k 0T ln⎜ ⎜ 2N ⎟ c ⎠ ⎝ ⎛ N c ⎞ 116 ⎛ Nc ⎞ ⎟⇒ ⎟ ⇒ ΔE D = k 0T ln⎜ = ln⎜ ⎜N ⎟ ⎜N ⎟ T ⎝ D⎠ ⎝ D⎠ 116 = ln 2 × 1015 × T 3 / 2 − ln N D T[()]分别将 N D＝1014 cm −3 ，N D＝1017 cm −3代入116 15 3/ 2 = ln 2 × 10 × T − ln N D T[()]可得其分别对应得温度为16K和55K。

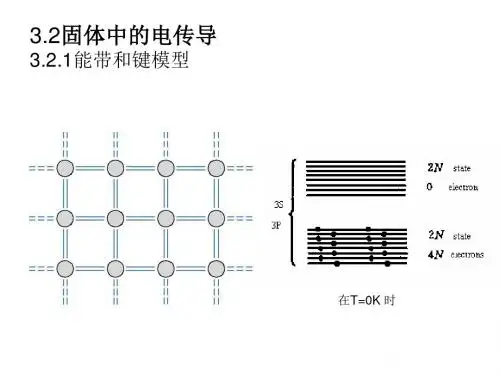
第二章半导体中的电子状态“If in discussing a semiconductor If in discussing a semiconductorp,y gy problem, you cannot draw an energy band diagram, then you don’t know what you are talking about.” Herbert KroemerHerbert Kroemer2.1 原子的结合和固体能带的形成2.2 半导体中的电子状态和能带2.3 半导体中的载流子运动及其有效质量2.3半导体中的载流子运动及其有效质量2.4回旋共振2.4 回旋共振2.5 Si和Ge的能带结构2.6 化合物半导体的能带结构2.7 杂质和缺陷能级2.7杂质和缺陷能级1.1 原子的结合和固体能带的形成(Bonds vs. Bands)(Bonds vs.Bands)2.2半导体中的电子状态和能带2.2 半导体中的电子状态和能带2.3 半导体中的载流子运动及其有效质量2.4 回旋共振2.4回旋共振2.5 Si和Ge的能带结构2.6 化合物半导体的能带结构2.7 杂质和缺陷能级2.7杂质和缺陷能级3s 2s1s氢原子结合成氢分子当两个氢原子非常接近时, 他们的电子波函数交叠，根据泡利不相容原理，两电子会相互作用，导致能级分裂成两个分立能级。

原子间的共价键相邻的两个原子各出一个电子在两个原子之间形成较大的电子云密度，通过它们对原子实的引力把两个原子结合在一起，形成共价键。

当价电子数目小于4时，形成的共价键数目就等于价电子数；当价电子数大于4时，形成的共价键数目等于8－N。

只能在电子云密度最大的方位形成非极性和极性共价键< 1化学键的离子性：0< fi非极性( f(=0)元素半导体：Si, Ge0 )i极性化合物半导体：III-V(GaAs),(),()II-V(CaTe), IV-IV(SiC)氢原子结合成氢分子ψσ＝ψ1s(r A)+ ψ1s(r B). 两个氢原子之间有较大的电子云密度。