电路串并联电路中电阻的关系

串、并联电路中的电阻关系（基础）责编：冯保国【学习目标】1.能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

2.理解欧姆定律，能运用欧姆定律进行简单的计算。

【要点梳理】要点一、等效电阻在电路中，如果一个电阻的效果和几个电阻在同一电路中的效果相同，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”对照理解。

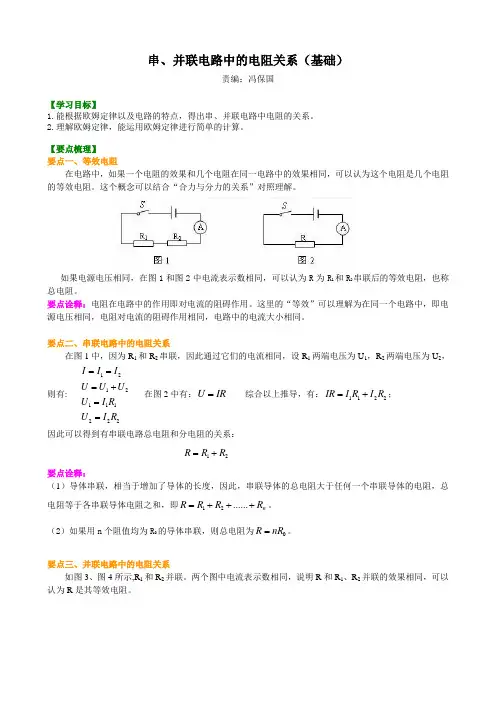
如果电源电压相同，在图1和图2中电流表示数相同，可以认为R 为R 1和R 2串联后的等效电阻，也称总电阻。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压相同，电阻对电流的阻碍作用相同，电路中的电流大小相同。

要点二、串联电路中的电阻关系在图1中，因为R 1和R 2串联，因此通过它们的电流相同，设R 1两端电压为U 1，R 2两端电压为U 2，则有:1212111222I I I U U U U I R U I R ===+== 在图2中有：U IR = 综合以上推导，有：1122IR I R I R =+；因此可以得到有串联电路总电阻和分电阻的关系：12R R R =+要点诠释：（1）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即12......n R R R R =+++。

（2）如果用n 个阻值均为R 0的导体串联，则总电阻为0R nR =。

要点三、并联电路中的电阻关系如图3、图4所示,R 1和R 2并联。

两个图中电流表示数相同，说明R 和R 1、R 2并联的效果相同，可以认为R 是其等效电阻。

在图3中，有 1212111222=I I I U U U U I R U I R =+===在图4中，有:UI R=综合以上推导，有1212U U U R R R =+;即：12111R R R =+ , 1212R R R R R =+要点诠释：（1）导体并联，相当于增大了导体的横截面积，因此，并联导体的总电阻小于任何一个并联导体的电阻，总电阻的倒数等于各并联导体电阻的倒数之和，即121111.....nR R R R =+++。

串、并联电路中的电阻关系一、等效电阻如图所示，U=3V，I=0.5A甲：电阻R1和R2的共同作用效果是使电路中的电流为0.5A。

乙：电阻R的作用效果也是使电路中的电流为0.5A。

在这种情况下，电阻R1和R2的共同作用效果和电阻R的作用效果是相同的，电阻R就是R1和的等效电阻。

R1、R2和R之间存在什么关系呢？二、串联电路中的电阻关系串联电路中，电流处处相等，总电压等于各部分电压之和。

甲：I = I1 = I2U=U1 + U2根据欧姆定律U1=I1R1U2=I2R2乙：U=IR两图中电源两端的电压相同，所以IR=IR1+IR2R=R1+R2串联电路中，等效电阻等于各串联电阻之和。

问题与思考甲：电阻R1和R2的共同作用效果是使电路中的电流为0.3A。

乙：电阻R的作用效果也是使电路中的电流为0.3A。

在这种情况下，电阻R1和R2的共同作用效果和电阻R的作用效果是相同的，所以，电阻R就是R1和R2的等效电阻。

如上图所示，把电阻并联起来，它们的等效电阻还等于各电阻之和吗？并联电路中，R=R1+R2 ???三、并联电路中的电阻关系并联电路中，总电流等于各支路中的电流之和，各支路两端的电压相等。

甲：I=I1+I2U=U1=U2根据欧姆定律I1=U1/R1I2=U2/R2乙：I=U/RU/R = U1/R1+ U2/R2= U/R1+ U/R21/R = 1/R1+ 1/R2并联电路中，等效电阻的倒数等于各并联电阻的倒数之和。

串联和并联是电路中常见的两种连接方式，它们在电流、电压和电阻之间有着不同的关系。

下面我们来详细了解一下串联和并联的电流、电压和电阻的关系。

一、串联电路的电流、电压和电阻关系1. 串联电路的电流：在串联电路中，电流只有一条路径可走，因此串联电路中的电流是相等的。

也就是说，串联电路中每个电阻上的电流都相同。

2. 串联电路的电压：在串联电路中，各个元件的电压之和等于总电压，即串联电路中的电压是相加的。

这是由基尔霍夫电压定律可得出的结论。

3. 串联电路的电阻：在串联电路中，各个电阻直接相加得到总电阻。

这也是由基尔霍夫电流定律可得出的结论。

二、并联电路的电流、电压和电阻关系1. 并联电路的电流：在并联电路中，电流可选择不同的路径进行流动，因此并联电路中的电流是分流的，即各个支路上的电流之和等于总电流。

2. 并联电路的电压：在并联电路中，各个支路上的电压相等，等于总电压。

也就是说，在并联电路中，各个支路上的电压相同。

3. 并联电路的电阻：在并联电路中，各个支路的电阻经过计算得到并联后的总电阻。

计算方式是利用电阻公式的倒数之和再取倒数。

三、串联和并联电路的不同之处1. 串联电路中的电流相等，电压相加，电阻直接相加；而并联电路中的电流分流，电压相等，电阻取倒数相加再取倒数。

2. 串联电路中的总电阻大于任意一个电阻的值，而并联电路中的总电阻小于任意一个电阻的值。

3. 串联电路中的总电压等于各个元件电压之和，而并联电路中的总电压等于各个支路的电压值。

串联和并联的电流、电压和电阻之间有着微妙的关系。

在实际应用中，根据不同的需求和情况，选择合适的串联或者并联连接方式来构建电路，是非常重要的。

对于电流、电压和电阻的关系要有清晰的理解，才能更好地分析和设计电路。

四、串并联混合电路的分析除了纯粹的串联电路和并联电路之外，还有一种常见的电路连接方式，即串并联混合电路。

在串并联混合电路中，电路中既有串联连接，又有并联连接。

这种情况下，需要对电流、电压和电阻进行更为复杂的分析。

串并联电路中电阻的关系如下：
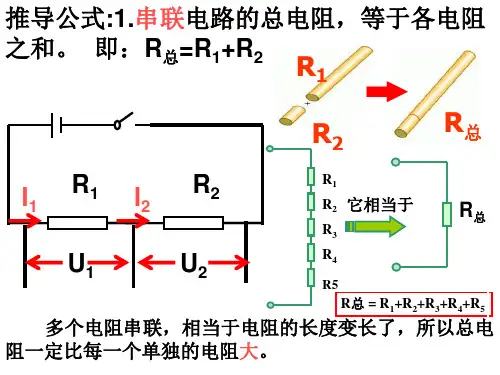
串联电路的总电阻等于各串联导体电阻之和，即R串＝R1+R2+-+Rn。

并联电路的总电阻的倒数等于各并联电阻的倒数和，即1／R并＝1／R1+1／R2+--+1／Rn。

串联电路的电阻和功率的关系
在串联电路中，由P=UI=I²R，I相同时，R越大，P越大。

即在串联电路中，电阻越大，实际电功率越大。

在并联电路中，P=UI=U²/R，U相同时，R越大，P越小。

所以在并联电路中，电阻越大，实际电功率越小。

电功率是作为表示电流做功快慢的物理量，一个用电器功率的大小数值上等于它在1秒内所消耗的电能。

如果在t（SI单位为J）这么长的时间内消耗的电能W（SI单位为J），那么这个用电器的电功率就是P=W/t。

电功率还等于导体两端电压与通过导体电流的乘积。

《聊聊串并联中电阻的关系》嘿，朋友！今天咱来唠唠串并联中电阻的关系。

这电阻啊，在电路里可重要了呢。

咱先说说串联吧。

啥是串联呢？就好比一群小伙伴手拉手排成一队。

在串联电路里，电阻们就像这些小伙伴一样，一个挨着一个。

那这时候电阻会有啥变化呢？嘿，你瞧，这时候总电阻就等于各个电阻之和。

比如说，有一个电阻是 3 欧姆，另一个是 5 欧姆，那它们串联起来，总电阻就是 3 加5，等于8 欧姆。

这就像小伙伴们一起使劲，力量就变大了一样。

再说说并联。

并联呢，就像是小伙伴们分成了几队，同时在干活。

在并联电路里，电阻们也有自己的特点。

总电阻的倒数等于各个电阻的倒数之和。

哎呀，听起来有点绕是不是？咱打个比方，有两个电阻，一个是 4 欧姆，一个是 6 欧姆。

咱先算出它们的倒数，4 欧姆的倒数是1/4，6 欧姆的倒数是1/6。

然后把这两个倒数加起来，得到的和再求倒数，就是并联后的总电阻啦。

算出来大概是2.4 欧姆。

这就像小伙伴们一起合作，效率就提高了呢。

那为啥会有这样的关系呢？咱可以这么想啊。

在串联的时候，电流只有一条路可走，就得挨个经过这些电阻，所以电阻就累加起来了。

而在并联的时候呢，电流可以分成好几路走，就像有好多小帮手一起帮忙，所以总电阻就变小了。

这串并联中电阻的关系可重要了呢。

在我们生活里也有很多地方能用到。

比如说家里的电器啊，有时候它们就是并联在电路里的，这样就算一个坏了，其他的还能正常工作。

要是不明白这电阻的关系，那电器出了问题可就不好修啦。

嘿嘿，现在你对串并联中电阻的关系有点了解了吧？下次看到电路的时候，你就可以想想这些电阻是怎么串并联的，它们的关系又是啥样的。

电路中的串并联与电阻的计算在电路中，串联和并联是两种常见的连接方式。

了解和掌握这两种连接方式以及电阻的计算方法对于电路设计和分析非常重要。

本文将详细介绍电路中的串并联以及电阻的计算方法。

一、串联电路串联电路是指将多个电器元件或电子元件按照顺序连接，其中每个元件都共享相同的电流。

在串联电路中，电流在所有电阻上都是相等的，而电压则会分配给每个电阻。

串联电路中的电阻值可以通过将各个电阻值相加来计算。

假设电路中有三个电阻，分别为 R1、R2 和 R3，则总电阻可以表示为 Rt = R1 + R2 + R3。

例如，如果电路中有三个电阻分别为10 Ω、20 Ω 和30 Ω，则总电阻为Rt = 10 Ω + 20 Ω + 30 Ω = 60 Ω。

二、并联电路并联电路是指将多个电器元件或电子元件同时连接到相同的两个节点上。

在并联电路中，电压在各个电阻上是相等的，而电流则会分配给每个电阻。

并联电路中的电阻值的倒数可以通过将各个电阻值的倒数相加再取倒数来计算。

假设电路中有三个电阻，分别为 R1、R2 和 R3，则总电阻可以表示为 Rt = 1 / (1/R1 + 1/R2 + 1/R3)。

例如，如果电路中有三个电阻分别为10 Ω、20 Ω 和30 Ω，则总电阻为Rt = 1 / (1/10 Ω + 1/20 Ω + 1/30 Ω)。

三、电阻的计算方法除了串并联电路中的电阻计算方法外，还有其他常见的电阻计算方法。

1. 如果电路中只有一个电阻，直接使用该电阻的阻值即可。

2. 如果电路中有多个相同的电阻，则可以使用简化公式来计算总电阻。

例如，如果电路中有 n 个相同的电阻，每个电阻的阻值为 R，则串联电路的总电阻为 Rt = nR，并联电路的总电阻为 Rt = R/n。

3. 如果电路中有多个电阻，但是它们之间没有串联或并联的关系，那么它们的总电阻就是各个电阻值之和。

总结：本文介绍了电路中的串并联以及电阻的计算方法。

串联电路中的电阻值可以通过将各个电阻值相加来计算，而并联电路中的电阻值的倒数可以通过将各个电阻值的倒数相加再取倒数来计算。

电路中的串联和并联关系在电路中，电器元件的连接方式有两种主要形式：串联和并联。

串联和并联是电路中基本的连接方式，它们的不同应用能够满足不同的电路需求。

一、串联连接串联连接是指将电器元件按照顺序依次连接在一起的方式。

在串联连接中，电流从一端进入第一个元件，经过每个元件，最后从另一端离开。

电流只能通过串联电路的每个元件，因此在串联连接中，电流保持不变。

1. 串联电阻的计算串联连接中的电阻可以通过简单相加来计算。

假设有三个串联电阻R1、R2和R3，它们的总电阻R总可以表示为R总 = R1 + R2 + R3。

2. 串联电压的分配在串联连接中，总电压会分配给每个电阻。

根据欧姆定律，电压与电阻成正比。

因此，如果有三个串联电阻R1、R2和R3，它们的电压分配比例可以表示为V1:V2:V3 = R1:R2:R3。

3. 串联电流的恒定在串联连接中，电流保持恒定。

这是因为电流只能通过每个元件，总电流等于各个电阻上的电流之和。

因此，如果有三个串联电阻R1、R2和R3，它们的电流相等。

二、并联连接并联连接是指将电器元件按照并列的方式连接在一起的方式。

在并联连接中，每个元件的一端连接在一起，另一端也连接在一起。

电流可以通过并联电路中的任何一个元件，因此在并联连接中，电流之和等于总电流。

1. 并联电阻的计算并联连接中的电阻可以通过简单求倒数再相加来计算。

假设有三个并联电阻R1、R2和R3，它们的总电阻R总可以表示为1/R总 = 1/R1 + 1/R2 + 1/R3。

2. 并联电压相同在并联连接中，各个元件上的电压相同。

这是因为多个元件连接在一起，它们的两个端点是连接的，因此它们的电势差相等。

3. 并联电流的计算在并联连接中，总电流等于各个元件上的电流之和。

如果有三个并联电阻R1、R2和R3，它们的电流分别为I1、I2和I3，则总电流I总= I1 + I2 + I3。

串联和并联连接在电路中应用广泛，可以根据实际需要选择合适的连接方式。

串联和并联电路是电路中常见的两种连接方式，它们在电流和电阻的关系上有着不同的特点。

在本文中，我将从深度和广度的角度探讨串联和并联电路中电流和电阻的关系，并共享我的个人观点和理解。

一、串联电路中电流和电阻的关系1. 串联电路的定义与特点在串联电路中，电气元件依次连接在电流的通路上，形成一个闭合回路。

电流只能顺序地通过每一个电气元件，因此串联电路中的电流是相同的，即I1=I2=I3。

在串联电路中，电阻则是依次相加的，即Rt=R1+R2+R3，这种关系在电路中非常常见。

2. 串联电路中电流和电阻的影响在串联电路中，电流和电阻之间存在着密切的关系。

根据欧姆定律，电流和电阻成正比，即I=V/R。

串联电路中的总电阻会影响电路中的总电流，而总电流又会影响电路中每个电气元件上的电压和功率。

在实际应用中，了解串联电路中电流和电阻的关系非常重要，可以帮助我们更好地设计和使用电路。

二、并联电路中电流和电阻的关系1. 并联电路的定义与特点在并联电路中，电气元件并排连接在电流的通路上，形成不同的并联支路。

由于并联支路的存在，电流可以同时通过不同的支路，因此并联电路中的电流是分流的，即I=I1+I2+I3。

而在并联电路中，各支路上的电压相同，这是并联电路的一大特点。

2. 并联电路中电流和电阻的影响在并联电路中，电流和电阻之间的关系与串联电路有所不同。

根据欧姆定律，电流和电阻成反比，即I=V/R。

在并联电路中，总电阻会影响电路中的总电流，而总电流又会影响电路中每个支路上的电压和功率。

了解并联电路中电流和电阻的关系，可以帮助我们更好地理解并应用电路中的电流分布和功率消耗。

三、个人观点和理解对于串联和并联电路中电流和电阻的关系，我认为它们既有相似之处，又有各自独特的特点。

在串联电路中，电阻是直接相加的，而在并联电路中，电阻是倒数相加再取倒数的。

这种不同的计算方式，导致了在串联和并联电路中电流和电阻的关系也存在着差异。

在实际应用中，我们需要根据具体的情况选择串联或并联连接方式，以实现所需的电流分布和功率消耗。

电阻的串并联与电路的等效电阻电路中的电阻是一种常见的元件，它用于控制电流的流动。

在电路设计和分析中，了解电阻的串并联以及电路的等效电阻是非常重要的。

本文将介绍电阻的串并联的概念，并探讨如何计算电路的等效电阻。

一、电阻的串联在电路中，当电阻按照一定的顺序连接在一起时，我们称之为电阻的串联。

串联的电阻会形成一个总电阻，总电阻等于各电阻之和。

例如，如果我们有三个电阻R1、R2和R3串联在一起，它们的阻值分别为R1，R2和R3。

那么总电阻RT可以通过下面的公式计算：RT = R1 + R2 + R3需要注意的是，电阻的串联不仅适用于三个电阻，也可以适用于任意数量的电阻。

总电阻等于每个电阻之间的阻值相加。

二、电阻的并联与电阻的串联相反，电阻的并联是指将多个电阻按照平行连接的方式连接在一起。

并联的电阻会形成一个总电阻，总电阻等于各电阻阻值的倒数之和的倒数。

假设我们有三个电阻R1、R2和R3并联在一起，它们的阻值分别为R1，R2和R3。

那么总电阻RT可以通过下面的公式计算：1/RT = 1/R1 + 1/R2 + 1/R3同样地，电阻的并联也适用于任意数量的电阻。

总电阻的倒数等于每个电阻的倒数之和的倒数。

三、电路的等效电阻在电路分析中，我们经常需要将一个复杂的电路简化为一个等效电阻。

等效电阻是一个能够代替原电路，使得原电路和等效电阻在外部电路中起到相同作用的电阻。

当电路中的电阻既有串联又有并联时，我们可以通过计算来求解电路的等效电阻。

首先，将电路中的电阻按照串联和并联的方式进行分组，然后计算每组的等效电阻。

最后，将这些等效电阻按照串联或并联的方式相连，就得到了整个电路的等效电阻。

举个例子，假设我们有一个电路，其中有两个电阻R1和R2串联在一起，再与一个电阻R3并联。

我们可以按照下面的步骤计算等效电阻：1. 先计算R1和R2的串联电阻，得到R12。

2. 再将R12与R3的并联电阻计算，得到整个电路的等效电阻RT。

串、并联电路中的电阻关系（基础）责编：冯保国【学习目标】1.能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

2.理解欧姆定律，能运用欧姆定律进行简单的计算。

【要点梳理】要点一、等效电阻在电路中，如果一个电阻的效果和几个电阻在同一电路中的效果相同，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”对照理解。

》如果电源电压相同，在图1和图2中电流表示数相同，可以认为R为R1和R2串联后的等效电阻，也称总电阻。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压相同，电阻对电流的阻碍作用相同，电路中的电流大小相同。

要点二、串联电路中的电阻关系在图1中，因为R1和R2串联，因此通过它们的电流相同，设R1两端电压为U1，R2两端电压为U2，则有:1212111222I I IU U UU I RU I R===+==在图2中有：U IR=综合以上推导，有：1122IR I R I R=+；因此可以得到有串联电路总电阻和分电阻的关系：12R R R=+要点诠释：（1）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即12......nR R R R=+++。

&（2）如果用n个阻值均为R0的导体串联，则总电阻为R nR=。

要点三、并联电路中的电阻关系如图3、图4所示,R1和R2并联。

两个图中电流表示数相同，说明R和R1、R2并联的效果相同，可以认为R是其等效电阻。

在图3中，有1212111222=I I IU U UUIRUIR=+===在图4中，有:UIR=综合以上推导，有1212U UUR R R=+;即：12111R R R=+, 1212R RRR R=+·要点诠释：（1）导体并联，相当于增大了导体的横截面积，因此，并联导体的总电阻小于任何一个并联导体的电阻，总电阻的倒数等于各并联导体电阻的倒数之和，即121111.....nR R R R=+++。

电阻并联与电阻串联的关系电阻是电学中常见的基本元件之一，它的特点是可以阻碍电流的流动。

在电路中，电阻并联与电阻串联是两种常见的连接方式。

本文将从理论和实际应用两方面来介绍电阻并联和电阻串联的关系。

一、电阻并联电阻并联是指将两个或多个电阻器的两端相连接，使它们的端点相同，从而形成一个新的电路。

电阻并联的电路图如图1所示。

在电阻并联中，每个电阻器的两端电压相同，而电流则分别流过每个电阻器。

因此，每个电阻器的电阻值越小，通过它的电流就越大。

整个电路的总电阻值等于各电阻器电阻值的倒数之和。

即：R总= 1/R1 + 1/R2 + … + 1/Rn其中，R1、R2、…、Rn为各电阻器的电阻值。

电阻并联的特点是总电阻值小于各电阻器中最小的电阻值，即电流可以更容易地通过整个电路。

因此，电阻并联常用于需要大电流通过的电路中，例如电子设备中的电源线路。

二、电阻串联电阻串联是指将两个或多个电阻器连接起来，形成一个新的电路，如图2所示。

在电阻串联中，电流从第一个电阻器流入，经过所有电阻器后再流出。

因此，每个电阻器的电流相同，而电压则分别降落在每个电阻器上。

整个电路的总电阻值等于各电阻器电阻值之和。

即：R总= R1 + R2 + … + Rn其中，R1、R2、…、Rn为各电阻器的电阻值。

电阻串联的特点是总电阻值大于各电阻器中最大的电阻值，即电流通过整个电路时会受到较大的阻碍。

因此，电阻串联常用于需要限制电流通过的电路中，例如LED灯的限流电路。

电阻并联与电阻串联是电路中常见的两种连接方式，它们的区别在于电阻器之间的连接方式不同。

在电阻并联中，电阻器的两端相连，电流分别流过每个电阻器；而在电阻串联中，电阻器依次连接，电流从第一个电阻器流入，经过所有电阻器后再流出。

电阻并联和电阻串联有一个重要的关系，即它们可以组合成更复杂的电路。

例如，在电子设备中，可以通过将多个电阻并联和电阻串联连接起来，形成各种不同的电路。

这些电路可以实现各种复杂的功能，例如滤波、放大、数字转换等。

电路中的串并联揭示电路中电阻的变化电路中的串并联：揭示电阻的变化电路是由电器元件组成的系统，利用电路可以实现电能的传输和转换。

在电路中，电阻是一种常见的电器元件，它具有阻碍电流流动的特性。

而串并联是电路中常见的两种连接方式，它们对电阻的变化产生了重要影响。

本文将揭示电路中串并联的工作原理，并探讨它们对电阻的影响。

一、串联电路在串联电路中，电器元件依次连接在同一路径上，电流从一个元件流过，再流入下一个元件。

串联电路中的电流是相同的，而电压则分摊在各个电阻上。

串联电路的总电阻等于各个电阻之和。

假设有三个串联的电阻R1、R2和R3，它们之间没有分支。

根据欧姆定律，串联电路中的总电阻可以表示为：R_total = R1 + R2 + R3因此，串联电路中的电阻随着元件数量的增加而增加，总电阻等于各个电阻的代数和。

二、并联电路在并联电路中，电器元件的两端连接在一起形成一个节点，电流分为不同路径通过这些元件。

并联电路中的电压相同，而电流则分摊在各个电阻上。

并联电路的总电阻可根据以下公式计算：1/R_total = 1/R1 + 1/R2 + 1/R3根据以上公式可知，并联电路中的总电阻小于各个电阻中最小的电阻。

并联电路中的电阻随着元件数量的增加而减小，总电阻小于各个电阻的倒数之和。

三、串并联的应用串联电路和并联电路都有各自的应用场景。

串联电路常用于需要控制电流的电路中，比如灯泡、加热器等。

由于串联电路中的总电流等于各个电阻上的电流之和，所以对于需要流过同样电流的元件，可以使用串联电路来控制。

而并联电路常用于需要控制电压的电路中，比如电子设备、计算机等。

由于并联电路中的总电压等于各个电阻上的电压，所以对于需要提供相同电压的元件，可以使用并联电路来控制。

此外，串并联电路也有应用。

例如，在电子电路中，常用串并联的方法来实现复杂的电路布局和功能。

通过合理组合串联电路和并联电路，可以实现电路中电阻的变化和调控，满足不同应用需求。