串联,并联电路中的电阻关系

串、并联电路中的电阻关系（基础）责编：冯保国【学习目标】1.能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

2.理解欧姆定律，能运用欧姆定律进行简单的计算。

【要点梳理】要点一、等效电阻在电路中，如果一个电阻的效果和几个电阻在同一电路中的效果相同，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”对照理解。

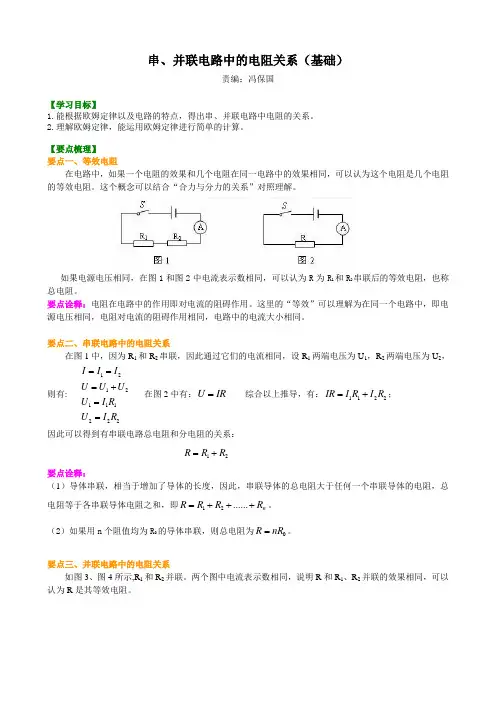
如果电源电压相同，在图1和图2中电流表示数相同，可以认为R 为R 1和R 2串联后的等效电阻，也称总电阻。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压相同，电阻对电流的阻碍作用相同，电路中的电流大小相同。

要点二、串联电路中的电阻关系在图1中，因为R 1和R 2串联，因此通过它们的电流相同，设R 1两端电压为U 1，R 2两端电压为U 2，则有:1212111222I I I U U U U I R U I R ===+== 在图2中有：U IR = 综合以上推导，有：1122IR I R I R =+；因此可以得到有串联电路总电阻和分电阻的关系：12R R R =+要点诠释：（1）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即12......n R R R R =+++。

（2）如果用n 个阻值均为R 0的导体串联，则总电阻为0R nR =。

要点三、并联电路中的电阻关系如图3、图4所示,R 1和R 2并联。

两个图中电流表示数相同，说明R 和R 1、R 2并联的效果相同，可以认为R 是其等效电阻。

在图3中，有 1212111222=I I I U U U U I R U I R =+===在图4中，有:UI R=综合以上推导，有1212U U U R R R =+;即：12111R R R =+ , 1212R R R R R =+要点诠释：（1）导体并联，相当于增大了导体的横截面积，因此，并联导体的总电阻小于任何一个并联导体的电阻，总电阻的倒数等于各并联导体电阻的倒数之和，即121111.....nR R R R =+++。

串、并联电路中的电阻关系一、等效电阻如图所示，U=3V，I=0.5A甲：电阻R1和R2的共同作用效果是使电路中的电流为0.5A。

乙：电阻R的作用效果也是使电路中的电流为0.5A。

在这种情况下，电阻R1和R2的共同作用效果和电阻R的作用效果是相同的，电阻R就是R1和的等效电阻。

R1、R2和R之间存在什么关系呢？二、串联电路中的电阻关系串联电路中，电流处处相等，总电压等于各部分电压之和。

甲：I = I1 = I2U=U1 + U2根据欧姆定律U1=I1R1U2=I2R2乙：U=IR两图中电源两端的电压相同，所以IR=IR1+IR2R=R1+R2串联电路中，等效电阻等于各串联电阻之和。

问题与思考甲：电阻R1和R2的共同作用效果是使电路中的电流为0.3A。

乙：电阻R的作用效果也是使电路中的电流为0.3A。

在这种情况下，电阻R1和R2的共同作用效果和电阻R的作用效果是相同的，所以，电阻R就是R1和R2的等效电阻。

如上图所示，把电阻并联起来，它们的等效电阻还等于各电阻之和吗？并联电路中，R=R1+R2 ???三、并联电路中的电阻关系并联电路中，总电流等于各支路中的电流之和，各支路两端的电压相等。

甲：I=I1+I2U=U1=U2根据欧姆定律I1=U1/R1I2=U2/R2乙：I=U/RU/R = U1/R1+ U2/R2= U/R1+ U/R21/R = 1/R1+ 1/R2并联电路中，等效电阻的倒数等于各并联电阻的倒数之和。

串并联电路中电阻的关系如下：
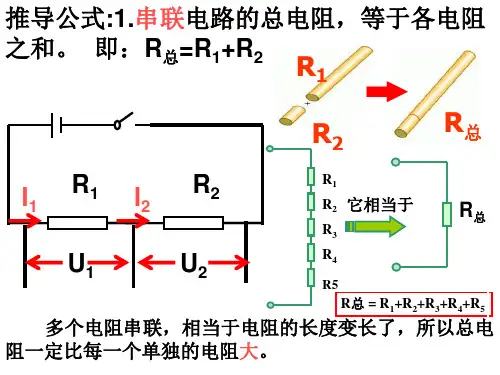
串联电路的总电阻等于各串联导体电阻之和，即R串＝R1+R2+-+Rn。

并联电路的总电阻的倒数等于各并联电阻的倒数和，即1／R并＝1／R1+1／R2+--+1／Rn。

串联电路的电阻和功率的关系
在串联电路中，由P=UI=I²R，I相同时，R越大，P越大。

即在串联电路中，电阻越大，实际电功率越大。

在并联电路中，P=UI=U²/R，U相同时，R越大，P越小。

所以在并联电路中，电阻越大，实际电功率越小。

电功率是作为表示电流做功快慢的物理量，一个用电器功率的大小数值上等于它在1秒内所消耗的电能。

如果在t（SI单位为J）这么长的时间内消耗的电能W（SI单位为J），那么这个用电器的电功率就是P=W/t。

电功率还等于导体两端电压与通过导体电流的乘积。

《聊聊串并联中电阻的关系》嘿，朋友！今天咱来唠唠串并联中电阻的关系。

这电阻啊，在电路里可重要了呢。

咱先说说串联吧。

啥是串联呢？就好比一群小伙伴手拉手排成一队。

在串联电路里，电阻们就像这些小伙伴一样，一个挨着一个。

那这时候电阻会有啥变化呢？嘿，你瞧，这时候总电阻就等于各个电阻之和。

比如说，有一个电阻是 3 欧姆，另一个是 5 欧姆，那它们串联起来，总电阻就是 3 加5，等于8 欧姆。

这就像小伙伴们一起使劲，力量就变大了一样。

再说说并联。

并联呢，就像是小伙伴们分成了几队，同时在干活。

在并联电路里，电阻们也有自己的特点。

总电阻的倒数等于各个电阻的倒数之和。

哎呀，听起来有点绕是不是？咱打个比方，有两个电阻，一个是 4 欧姆，一个是 6 欧姆。

咱先算出它们的倒数，4 欧姆的倒数是1/4，6 欧姆的倒数是1/6。

然后把这两个倒数加起来，得到的和再求倒数，就是并联后的总电阻啦。

算出来大概是2.4 欧姆。

这就像小伙伴们一起合作，效率就提高了呢。

那为啥会有这样的关系呢？咱可以这么想啊。

在串联的时候，电流只有一条路可走，就得挨个经过这些电阻，所以电阻就累加起来了。

而在并联的时候呢，电流可以分成好几路走，就像有好多小帮手一起帮忙，所以总电阻就变小了。

这串并联中电阻的关系可重要了呢。

在我们生活里也有很多地方能用到。

比如说家里的电器啊，有时候它们就是并联在电路里的，这样就算一个坏了，其他的还能正常工作。

要是不明白这电阻的关系，那电器出了问题可就不好修啦。

嘿嘿，现在你对串并联中电阻的关系有点了解了吧？下次看到电路的时候，你就可以想想这些电阻是怎么串并联的，它们的关系又是啥样的。

串、并联电路中的电阻关系（基础）责编：冯保国【学习目标】1.能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

*2.理解欧姆定律，能运用欧姆定律进行简单的计算。

【要点梳理】要点一、等效电阻在电路中，如果一个电阻的效果和几个电阻在同一电路中的效果相同，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”对照理解。

如果电源电压相同，在图1和图2中电流表示数相同，可以认为R为R1和R2串联后的等效电阻，也称总电阻。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压相同，电阻对电流的阻碍作用相同，电路中的电流大小相同。

]要点二、串联电路中的电阻关系在图1中，因为R1和R2串联，因此通过它们的电流相同，设R1两端电压为U1，R2两端电压为U2，则有:1212111222I I IU U UU I RU I R===+==在图2中有：U IR=综合以上推导，有：1122IR I R I R=+；因此可以得到有串联电路总电阻和分电阻的关系：12R R R=+要点诠释：（1）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即12......nR R R R=+++。

|（2）如果用n个阻值均为R0的导体串联，则总电阻为R nR=。

要点三、并联电路中的电阻关系如图3、图4所示,R1和R2并联。

两个图中电流表示数相同，说明R和R1、R2并联的效果相同，可以认为R是其等效电阻。

;在图3中，有12 12 111222=I I IU U UUIRUIR=+===在图4中，有:UIR=综合以上推导，有1212U UUR R R=+;即：12111R R R=+, 1212R RRR R=+要点诠释：（1）导体并联，相当于增大了导体的横截面积，因此，并联导体的总电阻小于任何一个并联导体的电阻，总电阻的倒数等于各并联导体电阻的倒数之和，即121111.....nR R R R=+++。

串联和并联电路是电路中常见的两种连接方式，它们在电流和电阻的关系上有着不同的特点。

在本文中，我将从深度和广度的角度探讨串联和并联电路中电流和电阻的关系，并共享我的个人观点和理解。

一、串联电路中电流和电阻的关系1. 串联电路的定义与特点在串联电路中，电气元件依次连接在电流的通路上，形成一个闭合回路。

电流只能顺序地通过每一个电气元件，因此串联电路中的电流是相同的，即I1=I2=I3。

在串联电路中，电阻则是依次相加的，即Rt=R1+R2+R3，这种关系在电路中非常常见。

2. 串联电路中电流和电阻的影响在串联电路中，电流和电阻之间存在着密切的关系。

根据欧姆定律，电流和电阻成正比，即I=V/R。

串联电路中的总电阻会影响电路中的总电流，而总电流又会影响电路中每个电气元件上的电压和功率。

在实际应用中，了解串联电路中电流和电阻的关系非常重要，可以帮助我们更好地设计和使用电路。

二、并联电路中电流和电阻的关系1. 并联电路的定义与特点在并联电路中，电气元件并排连接在电流的通路上，形成不同的并联支路。

由于并联支路的存在，电流可以同时通过不同的支路，因此并联电路中的电流是分流的，即I=I1+I2+I3。

而在并联电路中，各支路上的电压相同，这是并联电路的一大特点。

2. 并联电路中电流和电阻的影响在并联电路中，电流和电阻之间的关系与串联电路有所不同。

根据欧姆定律，电流和电阻成反比，即I=V/R。

在并联电路中，总电阻会影响电路中的总电流，而总电流又会影响电路中每个支路上的电压和功率。

了解并联电路中电流和电阻的关系，可以帮助我们更好地理解并应用电路中的电流分布和功率消耗。

三、个人观点和理解对于串联和并联电路中电流和电阻的关系，我认为它们既有相似之处，又有各自独特的特点。

在串联电路中，电阻是直接相加的，而在并联电路中，电阻是倒数相加再取倒数的。

这种不同的计算方式，导致了在串联和并联电路中电流和电阻的关系也存在着差异。

在实际应用中，我们需要根据具体的情况选择串联或并联连接方式，以实现所需的电流分布和功率消耗。

串联和并联电路中电流电压电阻的关系串联和并联电路是电路中常见的两种连接方式，它们在电流、电压和电阻上有着不同的关系。

我们来看串联电路。

串联电路是指将电器依次连接在一条路径上，电流经过电器时只有一条路径可以通过。

在串联电路中，电流是相同的，而电压则是根据各个电器的电阻来分配的。

假设有两个电器A和B，它们的电阻分别为R1和R2，电源的电压为V。

根据欧姆定律，我们可以得出串联电路中的电流和电压之间的关系。

根据欧姆定律，电流I等于电压V除以总电阻R，即I=V/R。

在串联电路中，总电阻R等于各个电器的电阻之和，即R=R1+R2。

所以电流I=V/(R1+R2)。

根据电压分配定律，在串联电路中，电压在各个电器上的分配与它们的电阻成正比。

假设电器A的电阻为R1，电器B的电阻为R2，电源的电压为V，那么电器A上的电压VA等于总电阻R1+R2与电源电压V的比例乘以V，即VA=(R1/(R1+R2))*V。

同理，电器B上的电压VB等于总电阻R1+R2与电源电压V的比例乘以V，即VB=(R2/(R1+R2))*V。

接下来，我们来看并联电路。

并联电路是指将电器同时连接在电源两端，电流可以分为多条路径通过。

在并联电路中，电流是根据各个电器的电阻来分配的，而电压则是相同的。

同样假设有两个电器A和B，它们的电阻分别为R1和R2，电源的电压为V。

根据欧姆定律，我们可以得出并联电路中的电流和电压之间的关系。

在并联电路中，各个电器的电压相同，等于电源的电压V。

所以电器A和电器B上的电压都等于V。

根据欧姆定律，电流I等于电压V除以电阻R，即I=V/R。

在并联电路中，总电流I等于各个电器上的电流之和，即I=IA+IB。

根据欧姆定律，电器A上的电流IA等于电压V除以电器A的电阻R1，即IA=V/R1；电器B上的电流IB等于电压V除以电器B的电阻R2，即IB=V/R2。

所以总电流I=V/R1+V/R2=V*(1/R1+1/R2)。

串联和并联电路中的电流、电压和电阻有着不同的关系。

串联电阻值和并联电阻值电阻是电路中常见的元件之一，可以用来限制电流的流动。

在电路中，电阻可以通过串联和并联的方式组合起来，以达到所需的电阻值。

串联电阻是指将多个电阻依次连接起来，电流从一个电阻流过后再流向下一个电阻。

这样，电流在各个电阻上产生的电压会依次累加，因此串联电阻的电阻值等于各个电阻值的和。

例如，如果有两个电阻R1和R2串联连接，它们的电阻值分别为R1和R2，则串联电阻的电阻值为R=R1+R2。

并联电阻是指将多个电阻同时连接在一起，它们的一端连接在一起，另一端连接在一起。

这样，电流在各个电阻上产生的电压相同，因此并联电阻的电阻值等于各个电阻值的倒数之和的倒数。

例如，如果有两个电阻R1和R2并联连接，它们的电阻值分别为R1和R2，则并联电阻的电阻值为R=1/(1/R1+1/R2)。

串联和并联电阻的组合可以帮助我们实现所需的电阻值。

对于串联电阻而言，当需要一个比较大的电阻值时，可以将多个较大的电阻串联连接起来；当需要一个比较小的电阻值时，可以将多个较小的电阻串联连接起来。

同理，对于并联电阻而言，当需要一个比较大的电阻值时，可以将多个较小的电阻并联连接起来；当需要一个比较小的电阻值时，可以将多个较大的电阻并联连接起来。

在实际应用中，串联电阻和并联电阻具有不同的特点和用途。

串联电阻常用于需要将电压分配到不同部分的电路中，例如使用电位器调节电路的电压；并联电阻常用于需要限制电流流动的电路中，例如使用限流电阻保护电路元件。

另外，串联电阻和并联电阻的计算方法也不同。

对于串联电阻，只需要将各个电阻的电阻值相加即可得到总电阻值；对于并联电阻，需要先将各个电阻的倒数相加，然后再将结果的倒数作为总电阻值。

这是因为电阻的计算是与电流、电压等物理量之间的关系有关的，而串联和并联电阻的连接方式导致了这种计算差异。

总的来说，串联和并联电阻的组合方式在电路设计和分析中起着重要的作用。

理解串联和并联电阻的原理和计算方法对于解决电路中的问题和优化电路设计都非常有帮助。

电路中的电阻和串并联关系电路中的电阻是指电流通过时产生的电阻力，用来限制电流的大小。

电阻是电路中常见的元件之一，可以通过串联和并联的方式连接在电路中。

本文将探讨电路中电阻的性质以及串并联关系。

一、电阻的基本性质电阻是通过电流通过时产生的电阻力，其大小由电阻值来表示，单位为欧姆（Ω）。

电阻值越大，表示电阻对电流的限制越强。

电阻的阻力大小与导线材料和结构有关。

常见的导线材料如铜、铝等，其电阻较小，适用于需要高导电性的场合。

而一些高电阻材料，如石墨、碳膜等，则适用于需要限制电流的场合。

电阻的结构也会影响其电阻值，如线圈状的电阻比直线状的电阻值大。

二、电阻的串联关系串联是指将多个电阻按照顺序连接在一起，电流依次通过每个电阻。

串联电阻的总电阻等于各个电阻之和。

假设有两个串联电阻R1和R2，电流从一端进入，然后经过R1和R2，最后从另一端流出。

根据欧姆定律，串联电阻的总电阻计算公式为：R总 = R1 + R2三、电阻的并联关系并联是指将多个电阻的一端连接在一起，另一端连接在一起，电流同时通过每个电阻。

并联电阻的总电阻等于各个电阻的倒数之和的倒数。

假设有两个并联电阻R1和R2，电流分为两路，经过R1和经过R2，然后再汇聚到一起。

根据欧姆定律，并联电阻的总电阻计算公式为：1/R总 = 1/R1 + 1/R2四、串并联的应用案例串并联电阻在电路中有着广泛的应用。

以下是一些常见的案例：1.亮度调节：在家用灯具中，通过串联或并联电阻来调节灯泡的亮度。

串联电阻可以通过增加电阻值来降低灯泡的亮度，而并联电阻则可以通过减小电阻值来提高亮度。

2.分压电路：在电路中，我们常常需要将电压进行分压，以满足电路中的元件对电压的要求。

串联电阻可以通过设置不同的电阻值来实现电压的分压。

3.电流限制：在一些需要限制电流的场合，可以通过串联电阻来达到控制电流的目的。

通过调整串联电阻的阻值，可以限制电路中的电流大小。

五、总结电路中的电阻和串并联关系是电路中的重要概念。