钢管截面特性计算

设计条件：1.计算依据《钢结构设计规范》 《变电站建筑结构设计技术规定》 《建筑地基基础设计规范》 《建筑结构荷载规范》 《建筑抗震设计规范》 《变电构架设计手册》 2．独立避雷针荷载计算： H=35m ， 第一段高度 h 1=7300mm, 采用钢管Φ 第二段高度 h 2=7000mm, 采用钢管Φ 第三段高度 h 3=7000mm, 采用钢管Φ 第四段高度 h 4=7000mm, 采用钢管Φ 第五段高度 h 5=2400mm, 采用钢管Φ 第六段高度h 6=1950mm, 采用钢管Φ 第七段高度 h 7=1600mm, 采用钢管Φ 第八段高度 h 5=1050mm, 采用钢管Φ按各段高度及外径求得加权平均外径为：D=(7300×535+7000×440+7000×340+7000× 240+2400×152+1950×133+1600×114+1050×95)÷(7300+7000×3+2400+1950+1600+1050)=339mm (实际取用 364mm 偏于安全) 风荷载计算：按《建筑结构荷载规范》 (GB 50009-2001 )( 2006版)查得ω 0=0.60kN/m 2， 风荷载标准值 ：ω k =βz. μ s . μ z . ω0风振系数：单钢管柱 (h>8m), β z =2.0 风压高度变化系数μ z ： h=35m 查《建筑结构荷载规范》 (GB50009-2001 )表 7.2.1( B 类)插值得： μ z =1.42+(1.56-1.42) ×5÷ (40-30)=1.4922风荷载体型系数μ s ：μ z ω 0.d =1.49× 0.60× 0.364 =0.118>0.015 ，取μ s =+0.62ωk =βz .μs . μz . ω 0=2.0×0.6× 1.49× 0.60=1.073kN/m作用于各段钢管的风荷载标准值：第一段钢管Φ 580/Φ 490x10， q 1= ω k xD=1.073 ×0.535=0.574 kN/m 第二段钢管Φ 490/Φ390x8，q 2=ω k xD=1.073 × 0.44=0.472 kN/m第三段钢管Φ 390/Φ290x8，q 3=ω k xD=1.073 × 0.34=0.365 kN/m 第四段钢管Φ 290/Φ190x6，q 4=ωkxD=1.073 × 0.24=0.258 kN/m避雷针计算GB50017-2003 NDGJ96-92 GB 50007-2002GB 50009-2001 (2006 年版) GB 50011-2008580/Φ 490x10，平均直径Φ 535，N=9.5 kN490/Φ 390x8，平均直径Φ 440， N=6 kN 390/Φ 290x7，平均直径Φ 340，N=5 kN290/Φ 190x6，平均直径Φ 240， N=2.5 kN 152x4， N=0.5 kN133x4， N=0.4 kN114x4， N=0.3 kN95x3， N=0.2 kN第五段钢管Φ152x4，q5=ωk xD=1.073 ×0.152=0.163 kN/m第六段钢管Φ133x4，q6=ωk xD=1.073 ×0.133=0.143 kN/m第七段钢管Φ114x4，q7= ω k xD=1.073 ×0.114=0.122 kN/m第八段钢管Φ95x3，q8=ωk xD=1.073 ×0.095=0.102 kN/m 、内力分析各段钢管底风荷载标准值：1) 剪力第八段钢管Q k8=0.102 × 1.05=0.107 kN第七段钢管Q k7=0.107+0.122 × 1.60=0.107+0.195=0.302 kN第六段钢管Q k6=0.302+0.143 × 1.95=0.302+0.279=0.581 kN第五段钢管Q k5=0.581+0.163 × 2.40=0.581+0.391=0.972 kN第四段钢管Q k4=0.972+0.258 × 7=0.972+1.806=2.778 kN第三段钢管Q k3=2.778+0.365 × 7=2.778+2.555=5.333 kN第二段钢管Q k2=5.333+0.472 × 7=5.333+3.304=8.637 kN第一段钢管Q k1=8.637+0.574 × 7.3=8.637+4.19=12.827 kN2) 弯矩第八段钢管M k8=0.5 ×1.05× 0.107=0.056 kNm第七段钢管M k7=0.056+0.107×1.6+0.5×1.6×0.195=0.056+0.171+0.156=0.383 kNm第六段钢管M k6=0.056+0.107×( 1.6+1.95) +0.156+0.195 × 1.95+0.5×1.95× 0.279=0.056+0.38+0.156+0.38+0.272=1.244 kNm第五段钢管M k5=0.056+0.107×(1.6+1.95+2.40)+0.156+0.195×( 1.95+2.40) +0.272+0.279 ×2.40+0.5×2.4× 0.391=0.056+0.637+0.156+0.85+0.272+0.67+0.469=3.574 kNm 第四段钢管M k4=0.056+0.107×(1.6+1.95+2.40+7)+0.156+0.195×( 1.95+2.40+7) +0.272+0.279 ×(2.40+7)+ 0.469+0.391 ×7+0.5×7×1.806=0.056+1.386+0.156+2.213+0.272+2.623+0.469+2.734+6.321=16.23 kNm第三段钢管M k3=0.056+0.107×(1.6+1.95+2.40+7+7 )+0.156+0.195×(1.95+2.40+7+7) +0.272+0.279 ×(2.40+7+7)+ 0.469+0.391 ×(7+7)+6.321+1.806 × 7+0.5 ×7×2.555=0.056+2.135+0.156+3.578+0.272+4.576+0.469+5.474+6.321+12.642+8.943=44.622 kNm第二段钢管M k2=0.056+0.107 ×( 1.6+1.95+2.40+7+7+7 )+0.156+0.195×( 1.95+2.40+7+7+7 )+0.272+0.279 × (2.40+7+7+7)+ 0.469+0.391 ×( 7+7+7) +6.321+1.806 ×(7+7)+8.943+2.555 × 7+0.5×7×3.304=0.056+2.884+0.156+4.943+0.272+6.529+0.469+8.211+6.321+25.284+8.943+17.885+11.564=95.517 kNm第一段钢管M k1=0.056+0.107×( 1.6+1.95+2.40+7+7+7+7.3 )+0.156+0.195 ×(1.95+2.40+7+7+7+7.3 )+0.272+0.279 × (2.40+7+7+7+7.3)+ 0.469+0.391 ×( 7+7+7+7.3 )+6.321+1.806×(7+7+7.3)+8.943+2.555 ×( 7+7.3 )+11.564+3.304×7.3+0.5×7.3×4.19=0.056+3.665+0.156+6.367+0.272+8.565+0.469+11.065+6.321+38.468+8.943+36.537 +11.564+24.119+15.294=171.862 kNm3）轴力第八段钢管N k8=0.2kN第七段钢管N k7=0.2+0.3=0.5kN第六段钢管N k6=0.5+0.4=0.9kN第五段钢管N k5=0.9+0.5=1.4kN第四段钢管N k4=1.4+2.5=3.9kN第三段钢管N k3=3.9+5=8.9kN第二段钢管N k2=8.9+6=14.9kN第一段钢管N k1=14.9+9.5=24.4kN三、钢管截面特性计算（按平均截面计算）第一段钢管Φ 580/Φ 490x10, 平均直径Φ 535 的截面特性I x=I y=π(d4-d41)/64=3.141592 ×(5354-5154)÷64=568453891.8mm4W x=W y=π(d4-d41)/(32d)=3.141592 ×(5354-5154)÷(32×535)=2125061.3mm3i x=i y=(d2+d21)0.5/4=(535 2+515 2)0.5÷ 4=185.7mm185.8A=π(d2-d21) /4=3.141592×(5352-5152) ÷4=16493.3 mm2第二段钢管Φ 490/Φ 390x8, 平均直径Φ 440 的截面特性I x=I y=π(d4-d41)/64=3.141592 ×(4404-4244)÷64=253366931.8mm4W x=W y=π(d4-d41)/(32d)=3.141592 ×(4404-4244)÷(32×440)=1151667.9mm3i x=i y=(d2+d21)0.5/4=(440 2+424 2)0.5÷ 4=152.8mmA=π(d2-d21) /4=3.141592×(4402-4242) ÷4=10857.3 mm2第三段钢管Φ 390/Φ 290x8, 平均直径Φ 340 的截面特性I x=I y=π(d4-d41)/64=3.141592 ×(3404-3244)÷64=115031326.3mm4W x=W y=π(d4-d41)/(32d)=3.141592 ×(3404-3244)÷(32×340)=676654.9mm3i x=i y=(d2+d21)0.5/4=(340 2+324 2)0.5÷ 4=117.4mmA=π(d2-d21) /4=3.141592 ×(3402-3242) ÷4=8344.1 mm2第四段钢管Φ 290/Φ 190x6, 平均直径Φ 340 的截面特性I x=I y=π(d4-d41)/64=3.141592 ×(2404-2284)÷64=30209536.1mm4W x=W y=π(d4-d41)/(32d)=3.141592 ×(2404-2284)÷(32×240)=251746.1mm3i x=i y=(d2+d21)0.5/4=(240 2+228 2)0.5÷ 4=82.8mmA=π(d2-d21) /4=3.141592 ×(2402-2242) ÷4=5830.8 mm2第五段钢管Φ 152×4 截面特性I x=I y=π(d4-d41)/64=3.141592 ×(1524-1444)÷64=5095913.6mm4W x=W y=π(d4-d41)/(32d)=3.141592 ×(1524-1444)÷(32×152)=67051.5mm3i x=i y=(d2+d21)0.5/4=(152 2+144 2)0.5÷ 4=52.3mmA=π(d2-d21) /4=3.141592 ×(1522-1442) ÷4=1859.8 mm2第六段钢管Φ 133x4 截面特性I x=I y=π(d4-d41)/64=3.141592 ×(1334-1254)÷64=3375252.6mm4W x=W y=π(d4-d41)/(32d)=3.141592×(1334-1254)÷(32x133)=50755.7mm 3i x=i y=(d2+d21)0.5/4=(133 2+125 2)0.5÷ 4=45.6mmA=π(d2-d21) /4=3.141592 ×(1332-1252) ÷4=1621 mm2第七段钢管Φ 114x4 截面特性I x=I y=π(d4-d41)/64=3.141592 ×(1144-1064)÷64=2093494.1mm 4W x=W y=π(d4-d41)/(32d)=3.141592 ×(1144-1064)÷(32×114)=36728mm3 i x=iy=(d2+d21)0.5/4=(1142+1062)0.5÷4=38.9mmA=π(d2-d21) /4=3.141592×(1142-1062) ÷4=1382.3 mm2第八段钢管Φ 95x3 截面特性I x=I y=π(d4-d41)/64=3.141592 ×(954-894)÷64=918345.5mm4W x=W y=π(d4-d41)/(32d)=3.141592×(954-894)÷(32×95)=193333.6mm 3 i x=iy=(d2+d21)0.5/4=(952+892)0.5÷4=32.5mmA=π(d2-d21) /4=3.141592×(952-892) ÷4=867.1mm 2四、强度验算第一段钢管N/A+M x/(γx W x)=1.2×24.4×1000÷16493.3+1.4×171.862×1000000÷(1.15×2125061.3)=1.78+98.46=100.24N/m m 2<215×0.7=150.5 N/mm2N/A-M x/(γx W x)=24.4 ×1000÷16493.3-1.4×171.862×1000000÷(1.15×2125061.3)=1.48-98.46=-96.98N/m m 2<215 ×0.7=150.5 N/mm 2第二段钢管N/A+M x/(γx W x)=1.2×14.9×1000÷10857.3 +1.4 ×95.517 ×1000000÷(1.15×1151667.9)=1.65+100.97=102.61N/m m 2<215 ×0.7=150.5 N/mmN/A-M x/(γx W x)= 14.9×1000÷10857.3 -95.517 ×1000000 ÷(1.15×1151667.9)=1.37-72.12=-70.75N/m m 2<215 × 0.7=150.5 N/mm 2 第三段钢管N/A+M x/(γx W x)= 1.2×8.9×1000÷8344.1 +1.4 ×44.622 ×1000000÷(1.15×676654.9)=1.28+80.28=81.56N/m m 2<215 ×0.7=150.5 N/mm N/A-M x/(γx W x)= 8.9×1000÷8344.1 -44.622×1000000÷(1.15×676654.9)=1.07-57.34=-56.27N/m m 2<215 ×0.7=150.5 N/mm 第四段钢管N/A+M x/(γx W x)= 1.2×3.9×1000÷5830.8 +1.4×16.23×1000000÷(1.15×251746.1)=0.8+78.48=79.28N/m m 2<215×0.7=150.5 N/mm N/A-M x/(γx W x)= 3.9×1000÷5830.8 -16.23×1000000÷(1.15×251746.1)=0.67-56.06=-55.39N/m m 2<215 ×0.7=150.5 N/mm 2第五段钢管N/A+M x/(γx W x)= 1.2×1.4×1000÷1859.8 +1.4×3.574×1000000÷(1.15×67051.5)=0.9+64.89=65.79N/m m 2<215×0.7=150.5 N/mm 2N/A-M x/(γx W x)= 1.4×1000÷1859.8-1.4×3.574×1000000÷(1.15×67051.5)=0.75-64.89=-64.14N/m m 2<215 ×0.7=150.5 N/mm 2第六段钢管N/A+M x/(γx W x)= 1.2×0.9×1000÷1621+1.4×1.244×1000000÷(1.15×50755.7)=0.67+29.84=30.51N/m m 2<215 ×0.7=150.5 N/mm 2 N/A-M x/(γx W x)= 0.9×1000÷1621-1.4×1.244×1000000÷(1.15×50755.7)=0.56-29.84=-29.28N/m m 2<215 ×0.7=150.5 N/mm 2第七段钢管N/A+M x/(γx W x)= 1.2×0.5×1000÷1382.3+1.4×0.383×1000000÷(1.15×36728)=0.43+12.69=13.12N/m m 2<215 ×0.7=150.5 N/mm 2 N/A-M x/(γx W x)= 0.5×1000÷1382.3-1.4×0.383×1000000÷(1.15×36728)=0.36-12.69=-12.33N/m m 2<215 ×0.7=150.5 N/mm 2第八段钢管设计值作用下：N/A+M x/(γx W x)= 1.2×0.2×1000÷1382.3+1.4×0.383×1000000÷(1.15×36728)=0.17+12.69=12.86N/m m 2<215 ×0.7=150.5 N/mm 2 N/A-M x/(γx W x)= 0.2×1000÷1382.3-1.4×0.383×1000000÷(1.15×36728)=0.14-12.69=-12.55N/m m 2<215 ×0.7=150.5 N/mm 2设计值作用下：N/A+M x/(γx W x)= 1.2×0.2×1000÷1382.3+0.383×1000000÷(1.15×36728)=0.17+9.07=9.24N/mm 2<80 N/mm 2N/A-M x/(γx W x)= 0.2×1000÷1382.3-1.4×0.383×1000000÷(1.15×36728)=0.14-12.69=-12.55N/mm 2<80 N/mm 2五、稳定性验算第一段钢管1）平面内的稳定性等效长度计算系数 K=1+M 1/M 2=1+95.517÷171.862=1.556注： (M 1为钢管上部弯矩； M 2为钢管下部弯矩 )x =Kl/i x =1.556×7300÷185.7=61.17<150,查得φx =0.815N 'Ex2EA /(1.1 2x ) 3.1415922 206000 16493.3/(1 .1 61.172) 81471312）平面外的稳定性2) 平面外的稳定性N tx M x 1.2 14900 1.4 1.0 95.517 1000000tx x0.7 2.10 81.27φx A φb W 1x 0.785 10857.3 1.0 1151667.9 83.37kN / m 215kN /m第三段钢管1）平面内的稳定性 等效长度计算系数 注： （M 1为钢管上部弯矩； M 2为钢管下部弯矩 ）mxMx φ A Nφx Ax W 1x (1 0.8 ' ) x 1xNE ' x1.2 24400 1.4 1.0 171.862 10000002.18 98.74100.92kN / m 0.815 16493.3215kN /m1.15 2125061.3 (1 0.8 1.2 24400 )8147131 )φx AtxM xφb W1x1.2 24400 0.815 16493.3 81.43kN /m 215kN /m0.7 1.4 1.0171.862 1000000 2.18 79.251.0 2125061.3第二段钢管1）平面内的稳定性等效长度计算系数K=1+M 1/M 2=1+44.622÷95.517=1.467注： （M 1为钢管上部弯矩； M 2为钢管下部弯矩 ）x =Kl/i x =1.467x7000 ÷ 152.8=67.21<150,查得φx =0.785N 'Ex 2EA /(1.1 x 2) 3.1415922 206000 10857.3 /(1.1 67.212 ) 4442507 NmxM x 1.2 14900φx A x W 1x (1 0.8 N ' ) 0.785 10857.3 x 1x NE 'x2.10 101.3 103.4kN /m 215kN /m1.4 1.0 95.517 10000001.2 149001.15 1151667.9 (1 0.8 )4442507K=1+M 1/M 2=1+16.23/44.622=1.36x =Kl/i x =1.36x7000 ÷ 117.4=81.09<150,查得φx =0.704N 'Ex 2EA/(1.1 2x ) 3.1415922 206000 8344.1 /(1.1 81.092) 2345411NmxMx1.2 8900 1.4 1.0 44.622 1000000φx Ax W 1x (10.8 N ' ) 0.704 8344.11.15 676654.9 (1 0.81.2 8900) N E 'x23454111.82 80.57 82.39kN /m215kN /m2)平面外的稳定性N tx M x 1.2 8900 0.7 1.4 1.044.622 100000064.61.82φx A φb W 1x 0.704 8344.1 1.0 676654.966.42kN /m 215kN /m第四段钢管1) 平面内的稳定性等效长度计算系数 K=1+M 1/M 2=1+3.574 ÷ 16.23=1.22 注： (M 1为钢管上部弯矩； M 2为钢管下部弯矩 )x =Kl/i x =1.22x7000 ÷ 82.8=103.14<150,查得φx =0.56364.37kN/m 215kN /m根据上述结构计算，第五、第六、第七、第八段平面内及平面外都满足要求。

钢管支架计算书天津海河大桥钢箱梁吊装时，需在M19节段吊装过程中搭设钢管移动支架，下面根据支架搭设方案进行计算：1、荷载计算M19节段重量为187.08T,整体受力。

2、计算钢管支架的轴力据提供的数据：P总=1870.8KN，钢管支架自重为450KN，则最下面钢管所承受的最大轴力为：N=2320.8KN,取N=2400KN进行控制计算3、验算钢管的强度（4Φ720，D=10MM）钢管支架的强度验算由下式计算：N/Am<[б]б=N/Am =2400/（4×223）=2.69KN/cm2 б=N/Am=2400/（4×194.7）=3.08KN/cm2而[б]=170Mpa=17 KN/cm2，故安全。

4、整体稳定性验算钢管支架的整体稳定性由下式计算：N/Am<ψ[б](1)截面力学特性（如下图）钢管支架截面力学特性计算图（尺寸单位：cm）如图所示，立柱由4Φ720，d=10mm的钢管组成，查表有A m =223cm2,IX/=140579.2cm4 Am=194.7cm2,IX/=93639.59cm4I X =4×(IX/+Am×r22)=4×(140579.2+3102×223) =86283516.8cm4I X =4×(IX/+Am×r22)=4×(93639.59+3102×194.7) =75217238cm4（2）：计算整体稳定性折减系数计算构件的长细比λh：由《钢结构设计手册》查得格构式压弯杆件的长细比计算公式：λh =(λ2+27Ad/Aq)1/2 λh=(λ2+27Ad/Aq)1/2λ0 =L/i=3600/25.1=143.42 λ=L/i=3600/21.93=164.16 26948.505651273.76 Ad =1218.4cm2 Ad=83390.66cm235887.76 Aq =2×4800=864cm2 Aq=71706.72cm2代入计算有λh =143.4 代人计算有λh=164.2查《钢结构设计手册》附表，得ψ1=0.339 ψ1=0.273(3)立柱的整体稳定性验算由公式有：N/Am<ψ[б]б=N/Am =2400/（4×223）=2.69KN/cm2 б=N/Am=2400/（4×194.7）=3.08KN/cm2ψ[б]=0.273×170=46.4Mpa=4.6KN/cm2而ψ[б]=0.339×170=57.6Mpa=5.6KN/cm2，故安全。

钢管力学性能力学性能钢材力学性能是保证钢材最终使用性能（机械性能）的重要指标，它取决于钢的化学成分和热处理制度。

在钢管标准中，根据不同的使用要求，规定了拉伸性能（抗拉强度、屈服强度或屈服点、伸长率）以及硬度、韧性指标，还有用户要求的高、低温性能等。

①抗拉强度（σb）试样在拉伸过程中，在拉断时所承受的最大力（Fb），出以试样原横截面积（So）所得的应力（σ），称为抗拉强度（σb），单位为N/mm2（MPa）。

它表示金属材料在拉力作用下抵抗破坏的最大能力。

计算公式为：式中：Fb--试样拉断时所承受的最大力，N（牛顿）； So--试样原始横截面积，mm2。

②屈服点（σs）具有屈服现象的金属材料，试样在拉伸过程中力不增加（保持恒定）仍能继续伸长时的应力，称屈服点。

若力发生下降时，则应区分上、下屈服点。

屈服点的单位为N/mm2（MPa）。

上屈服点（σsu）：试样发生屈服而力首次下降前的最大应力；下屈服点（σsl）：当不计初始瞬时效应时，屈服阶段中的最小应力。

屈服点的计算公式为：式中：Fs--试样拉伸过程中屈服力（恒定），N（牛顿）So--试样原始横截面积，mm2。

③断后伸长率（σ）在拉伸试验中，试样拉断后其标距所增加的长度与原标距长度的百分比，称为伸长率。

以σ表示，单位为%。

计算公式为：式中：L1--试样拉断后的标距长度，mm； L0--试样原始标距长度，mm。

④断面收缩率（ψ）在拉伸试验中，试样拉断后其缩径处横截面积的最大缩减量与原始横截面积的百分比，称为断面收缩率。

以ψ表示，单位为%。

计算公式如下：式中：S0--试样原始横截面积，mm2； S1--试样拉断后缩径处的最少横截面积，mm2。

⑤硬度指标金属材料抵抗硬的物体压陷表面的能力，称为硬度。

根据试验方法和适用范围不同，硬度又可分为布氏硬度、洛氏硬度、维氏硬度、肖氏硬度、显微硬度和高温硬度等。

对于管材一般常用的有布氏、洛氏、维氏硬度三种。

A、布氏硬度（HB）用一定直径的钢球或硬质合金球，以规定的试验力（F）压入式样表面，经规定保持时间后卸除试验力，测量试样表面的压痕直径（L）。

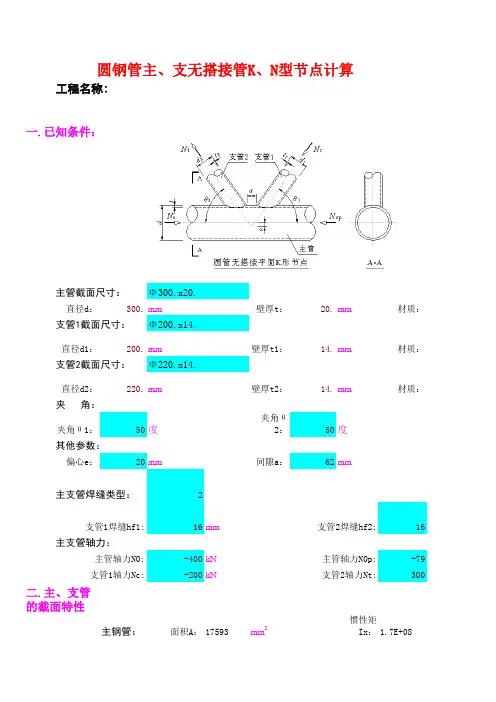
9. 施工验算9.1屋面梁支承台架根据屋面梁支承台架的平面布置情况和受力情况，屋面梁支承台架拟采用截面形式为Φ609×12的焊接钢管。

9.1.1截面特性A=πdt=π×597×12=22506mm2i x=i y=0.35d=0.35×597=208.95mm=20.9cmλ=l/i，截面为b类。

9.1.2承载力计算l=15m时, λ=l/i=1500/20.9=71.8, 查表得φ=0.74N=φAf=0.74×22506×215=3580745N=3580.7KNl=20m时, λ=l/i=2000/20.9=95.7, 查表得φ=0.583N=φAf=0.583×22506×215=2821015N=2821KNl=25m时, λ=l/i=2500/20.9=119.6, 查表得φ=0.439N=φAf=0.439×22506×215=2124229N=2124.2KNl=30m时, λ=l/i=3000/20.9=143.5, 查表得φ=0.331N=φAf=0.331×22506×215=1601639N=1601.6KNl=35m时, λ=l/i=3500/20.9=167.5，查表得φ=0.255N=φAf=0.255×22506×215=1233891N=1233.9KN9.2主拱支承台架根据主拱的分段情况和主拱支承台架的平面布置情况，主拱支承台架拟选用由角钢组成的格构式支架，如图所示：9.2.1组合截面规格为1000×1000组合截面规格为1000×1000，单肢采用L90×8的角钢、缀条采用L63×8的角钢，缀条间距为1m。

①截面特性角钢L63×8的截面特性：A=9.51cm2、I x=34.5cm4、i x=1.90cm、i x0=2.4cm、i y0=1.23cm、z=1.85cm角钢L90×8的截面特性：A=13.9cm2I x=109cm4 、i x=2.76cm、i x0=3.48cmI y=I xi y=i x=√(长细比A/A1x=(4×A/A1y=(4×λ1max②承载力计算l=15m时, λx=λy=l/i=1500/47.6=31.5换算长细比λ0x=λ0y=33.3, 查表得φ=0.924N=φAf=1104549N=1104.5KNl=20m时, λx=λy=l/i=2000/47.6=42换算长细比λ0x=λ0y=43.4, 查表得φ=0.885N=φAf=1057929N=1057.9KNl=25m时, λx=λy=l/i=2500/47.6=52.5换算长细比λ0x=λ0y=53.6, 查表得φ=0.84N=φAf=1004136N=1004.1KNl=30m时, λx=λy=l/i=3000/47.6=63换算长细比λ0x=λ0y=63.9, 查表得φ=0.786N=φAf=939584N=939.6KNl=35m时, λx=λy =l/i=3500/47.6=73.5换算长细比λ0x=λ0y=74.3, 查表得φ=0.724N=φAf=865469N=865.5KN③单肢承载力λ1=l1/i1=1000/17.8=56.2，查表得φ1=0.827N1=φ1A1F=247149N=247.1KN9.2.2组合截面规格为1500×1500组合截面规格为1500×1500，单肢采用L90×8的角钢、缀条采用L63×8的角钢，缀条间距为1m。

第1章钢便桥计算书1.1受力模型及材料参数钢栈桥验算采用有限元法，选取便桥的标准跨径作为计算模型，利用midas Civil 2019计算程序建模进行验算。

1.1.1跨径9m单排3根桩钢便桥结构模型图1.1-2 跨径9m单排3根桩便桥结构模型桥型1：栈桥上部结构为贝雷梁结构，下部结构为钢管桩加型钢承重梁结构。

栈桥基础及桥墩全部采用φ630mm厚10mm的螺旋焊接钢管桩，钢管桩按单排3根桩桩布置。

横联及斜撑采用[20a槽钢，钢管桩顶设双拼I45a工字钢帽梁。

桩顶横梁上架设贝雷梁，采用单层3组每组2片总计6片贝雷架结构，每组贝雷架采用定制支撑架连接，相邻贝雷架组采用∠75×8角钢连接，间距为90+125+90+125+90cm形成主纵梁，贝雷梁上设按30㎝间距布置I25a工字钢分配横梁与桥面10mm厚钢板经焊接固定成型的6m宽模块。

1.1.2材料参数铺装钢板厚度10mm，材料Q235钢。

分配横梁参数：材料Q235钢，截面I25a，长度6m。

主梁参数：采用321型贝雷片，材料为16Mn钢。

贝雷梁支撑架参数：材料Q235，材料为∠63×4角钢。

贝雷梁组间斜撑参数：材料Q235，材料为∠75×8角钢。

桩顶横梁参数：材料Q235钢，截面2×I45a，长度6m。

钢管桩参数：材料Q235钢，管型截面（外径630mm，厚度10mm）长度为13.4m。

根据《钢结构设计标准》GB50017-2017，钢材强度设计值可查表得：型钢材质均为Q235钢，其抗弯设计强度a 215][MP =σ，抗剪设计强度[]a 125MP =τ。

贝雷片材质为16Mn 钢，其容许弯应力[]a 273MP =σ，容许剪应力[]a 156MP =τ。

根据《公路钢结构桥梁设计规范》JTG D64-2015，挠度计算可查表得：2.边界条件钢管桩的底部固结；桩顶横梁和钢管桩采用弹性连接(刚性)； 桩顶横梁和贝雷片弹性连接(刚性)； 贝雷片和分配横梁采用弹性连接(刚性)。

轴抗弯强度计算公式12则抗弯强度计算公式(一)工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式: 简支梁2、荷载受力形式: 简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN工字钢抗弯强度计算方法二、选择受荷截面11、截面类型: 工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3 G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm工字钢抗弯强度计算方法三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制〔v〕:L/250工字钢抗弯强度计算方法四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156 KN.M工字钢抗弯强度计算方法五、强度及刚度验算结果21、弯曲正应力ζmax = Mmax / (γx * Wx),124.85 N/mm22、A处剪应力ηA = RA * Sx / (Ix * tw),10.69 N/mm23、B处剪应力ηB = RB * Sx / (Ix * tw),10.69 N/毫米为单位，直接把数值代入上述公式，得出即为每米方管的重量，以克为单位。

如30x30x2.5毫米的方管，按上述公式即可算出其每米重量为:4x2.5x(30-2.5)x7.85=275x7.85=2158.75克，即约2.16公斤矩管抗弯强度计算公式1、先计算截面模量WX=(a四次方-b四次方)/6a2、再根据所选材料的强度，计算所能承受的弯矩3、与梁上载荷所形成的弯矩比对，看看是否在安全范围内参见《机械设计手册》机械工业出版社2007年12月版第一卷第1-59页玻璃的抗弯强度计算公式锦泰特种玻璃生产的玻璃的抗弯强度一般在60~220Mpa之间，玻璃样品的形式和表面状态对测试的结果影响较大，3通常采用万能压力测试仪测试。

高支模方案的设计计算规则支模及模板系统的选择1) 、扣件式钢管脚手架采用的钢材应符合Q235-A 级钢的规定，每根钢管的最大质量不应大于25kg,宜采 用①48 X 3.5钢管。

所选用的钢管规格及截面特性见下表:钢管规格及截面特性钢材的强度设计值与弹性模量(N/mm 2)2) 、门式脚手架采用的钢材应符合 Q235-A 级钢的规定。

工程中一般采用门架型号为MF1217及承托架BF617。

其主要几何尺寸、扣件规格、配件规格及钢管截面几何特性见下表。

1、支模系统选用的材料、规格及截面特性MF1219、常用的门架的规格及重量门架钢管截面几何特性1) 、胶合板规格2）、木枋规格：3) 、木枋的力学性能：广东地区一般使用松木，下面式马尾松的力学性能马尾松的力学性能2、模板系统选用的材料、规格及截面特性厚度(mm )12, 15， 18高支模的计算及验算1、支撑系统的设计1）、扣件式脚手架支模系统的设计根据支模的高度、荷载、使用面积进行设计。

包括：支撑钢管的选型、排距、搭设层数、纵横水平拉杆及剪刀撑的设置，构造要求应符合规范JGJ130-2001第6.8条的规定。

计算步骤:a、计算单元单根立杆的计算面积：S=L1 X L2b、荷载计算b.1 一个柱距范围内脚手架自重产生的轴向力N GK1N G1K=g l X Hg1：为一个柱距范围内每米脚手架自重产生的轴向力标准值H:脚手架的支撑高度g i包括立柱、纵横向水平杆、连接它们的扣件重。

可参考下表数据b.2模板自重标准值:根据实际设计进行计算。

一般对于肋形楼板模板，自重标准值可参考下表:楼板模板自重标准值g2（KN/mm2）b.3新浇混凝土自重标准值：g3q2 一般取25KN/mm3。

b.4钢筋自重标准值：g4钢筋设计标准值应根据设计图纸确定。

对于一般梁板结构每立方米钢筋混凝土的钢筋自重标准值可采用以下数值梁截面面积t:楼板的厚度mmb.5单根立管承受的恒荷载工N G K= N G1K+(g2+g3+g4)X Sb.6施工人员及施工设备荷载q iq1 一般取：1.0KN/m2 b.7振捣混凝土时产生的荷载q2q2 一般取：2.0KN/m2 b.8单根立管承受的活荷载2 N QK= (q什q2)X SC、模板支架立杆的轴向力设计值不考虑风荷载时：N=1.22 N GK+1.42N QK d立杆的稳定性计算计算公式：N/（①A）三f即：N三①A f①：轴心受压构件的稳定系数：根据长细比查JGJ130-2001附录C入：长细比，入=10 / iI o :计算长度l0= h+2a a:模板支架立杆伸出顶层横向水平杆中心线至模板支撑点的长度i:回转半径A :立杆的截面积f：钢材的抗压强度设计值附表：根据以上公式及参数，分别计算步距为2仆、1.8m、1.6m、1.4m、1.2m、1.0m的立杆稳定承载力。

钢管混凝土组合截面计算方法及其在midas 中的实现作者：武庆喜代金鹏葛勇来源：《时代经贸》2013年第24期【摘要】根据弹性理论对钢管混凝土组合构件截面应力及截面内力进行计算推导，结合实际工程计算了钢管混凝土拱桥拱肋应力及内力，并用midas软件模拟组合截面受力状态，分析了软件模拟时应注意的问题。

【关键词】钢管混凝土；组合构件；换算截面；midas模拟一、引言钢管混凝土组合结构出现至今已经有近100年的历史，我国在60年代初期开始研究这种结构，90年代后，钢管混凝土在拱桥结构中大量应用，产生了良好的经济效益和美学效果。

钢管混凝土组合结构是由普通混凝土填入薄壁圆形钢管内而形成的组合结构，钢管内填混凝土增强了钢管壁的局部稳定性，钢管对核心混凝土的套箍约束作用，使其处于三向受压状态，薄壁钢管与核心混凝土相互弥补了彼此弱点，并且充分发挥各自优点，从而使得钢管混凝土组合结构具有更高的抗压强度和更好的变形能力。

通常情况下，钢管混凝土是在其弹性范围内工作的，可按弹性理论进行设计计算。

二、组合截面内力计算原理1.弹性理论基本假设钢—混凝土组合结构弹性设计的主要计算内容是组合截面应力应变，确保结构的截面强度、刚度和稳定性，截面应力计算是最核心内容。

按弹性理论计算钢—混凝土组合结构时，做下列假设：（1）完全弹性假设，钢材和混凝土都在弹性变形范围内工作。

（2）平截面假设，组合梁在受力弯曲后，其原来的横截面仍为平面，并绕垂直于纵对称面的某一轴旋转，且垂直于梁变形后的轴线。

（3）两种材料之间连接可靠，无相对滑移。

基本假设与材料力学中采用的基本假设一致，因而原则上可以利用材料力学公式计算组合截面的应力和变形。

2.截面特性换算钢—混凝土组合结构是两种不同性质的材料组合的复合结构，因此首先解决截面换算问题，即将两种材料换算为具有相同弹性模量的同一种材料。

在钢—混凝土组合结构计算时，通常将混凝土截面用等效的钢材截面代替，这种代替后的截面称为换算截面。

立杆钢管截面回转半径 i(cm)立杆钢管截面回转半径是指在钢管的截面上任意一点离截面重心的距离。

在工程设计和施工过程中，立杆钢管的截面回转半径是一个重要的参数。

本文将介绍立杆钢管截面回转半径的定义、计算方法以及在实际工程中的应用。

一、立杆钢管截面回转半径的定义立杆钢管是一种圆柱状的管材，其截面通常为圆形或方形。

立杆钢管的截面回转半径是指在立杆钢管的截面上，从截面的重心到任意一点的距离。

具体而言，对于圆形截面的立杆钢管，截面回转半径即为任意一点到截面重心的距离。

对于方形截面的立杆钢管，截面回转半径则是指从截面重心到截面四个角落的距离的平均值。

二、立杆钢管截面回转半径的计算方法计算立杆钢管截面回转半径的方法有很多种。

根据立杆钢管的截面形状不同，计算方法也有所不同。

以下是常见的计算方法：1.圆形截面的立杆钢管对于圆形截面的立杆钢管，可以采用以下公式计算截面回转半径：i = d/2其中，i为截面回转半径，d为立杆钢管的直径。

2.方形截面的立杆钢管对于方形截面的立杆钢管，截面回转半径需要考虑截面四个角落的距离。

具体而言，可采用以下公式计算截面回转半径：i = (a + b)/6其中，i为截面回转半径，a为立杆钢管的宽度，b为立杆钢管的高度。

需要注意的是，这里只是简要介绍了常见的计算方法，实际在工程中，还需要根据具体的要求和设计标准进行计算。

三、立杆钢管截面回转半径在实际工程中的应用立杆钢管截面回转半径在实际工程中具有广泛的应用。

下面介绍一些常见的应用领域：1.结构设计在进行钢结构的设计过程中，需要考虑立杆钢管的截面回转半径。

根据结构的要求和设计标准，可以选择合适的立杆钢管截面形状和尺寸。

截面回转半径是结构设计的重要参考参数之一。

2.强度计算立杆钢管的截面回转半径与其强度有密切关系。

回转半径越大，钢管的强度也会相应提高。

在工程中，需要根据钢管的截面回转半径来计算其承载力和变形能力等。

3.施工安装在立杆钢管的施工安装过程中，截面回转半径也是一个重要的考虑因素。

φ146乘以5.0钢管对x轴的净截面模量解释说明1. 引言1.1 概述本文旨在对φ146乘以5.0钢管对x轴的净截面模量进行解释和说明。

净截面模量是一个物体抵抗变形的性质，它描述了该物体在外力作用下产生弯曲时的刚度。

1.2 文章结构本文分为引言、正文、要点一、要点二和结论五个部分。

在引言中，我们将介绍文章的概述、结构和目的。

正文将详细叙述φ146乘以5.0钢管对x轴的净截面模量相关内容，而要点一和要点二将进一步探讨该钢管的特点和应用领域。

最后，在结论部分，我们总结所得结果并进行相关分析。

1.3 目的我们撰写这篇文章的目的是深入解释φ146乘以5.0钢管对x轴的净截面模量，并向读者展示该参数在工程实践中的重要性与应用前景。

通过本文，读者将能够理解该钢管在不同场景下承受外力时的变形特性，并了解其在建筑、航空航天等领域中具有广泛应用价值。

2. 正文在本研究中，我们将讨论φ146乘以5.0钢管对x轴的净截面模量。

首先，让我们来了解一下什么是净截面模量。

净截面模量是材料在受力作用下产生弯曲时其抵抗变形能力的一个重要参数。

它代表了截面内部纤维之间相对位置的特征，是衡量材料刚度和强度的关键指标之一。

φ146乘以5.0钢管是一种常见的工程材料，具有较高的强度和刚度。

它被广泛应用于建筑、桥梁和机械工程等领域。

对于物体在x轴方向受力产生弯曲时，其净截面模量可以通过以下公式计算：J = (π/32) * (D^4 - d^4)其中，J表示净截面模量，D表示外径，d表示内径。

对于φ146乘以5.0钢管而言，其外径为146mm（即D=146mm），内径根据不同规格可进行相应调整（即d可能不同）。

带入上述公式可得到该钢管在x轴方向的净截面模量。

接下来，我们将重点探讨净截面模量的影响因素以及其在工程中的应用。

首先，截面形状是影响净截面模量的重要因素之一。

不同几何形状的截面将表现出不同的刚度和强度特性。

其次，材料的选择也会对净截面模量产生显著影响。

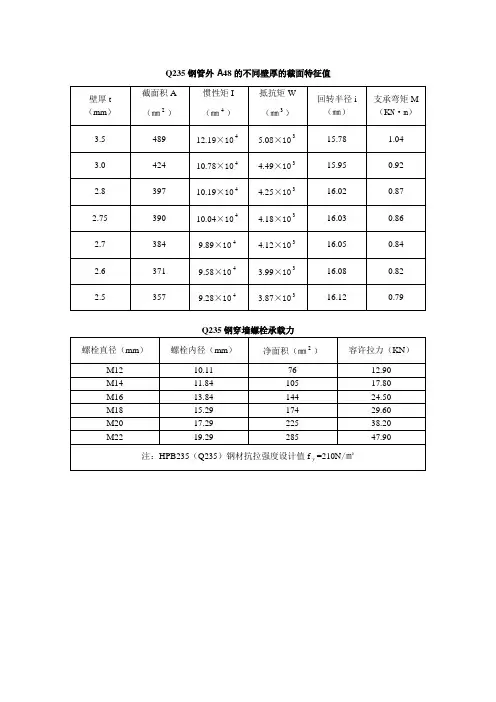
双井圩大桥第6、7、10跨现浇箱梁支架计算书一、有关力学参数1、碗扣件钢管截面特性:①、外径d=48mm②、壁厚t=3.5mm③、截面面积A=489mm2④、惯性矩I=121500mm5⑤、抵抗矩W=5078mm3⑥、回转半径i=15.78mm⑦、每米长自重=38.4N⑧、钢材弹性模量E=2.1×105Mpa2、松木材①、顺纹容许弯应力[σw]=12Mpa②、弹性模量E=9×103Mpa3、杉木材①、顺纹容许弯应力[σw]=13Mpa②、弹性模量E=10×103Mpa二、梁体空箱段以第7跨为算例,立杆横向间l1=60cm,纵向间距l2=90cm1、计算荷载砼输送泵出口砼冲击产生的荷载=4 kN/㎡振动器产生的垂直于模板的荷载=3kN/㎡施工人员及料具，胶合板，方木自重产生的荷载=5 KN/㎡梁体容重取γ=26 KN/m3，取1m长的箱梁计算，截面面积=8.29㎡，底面6.75m 故梁体荷载=26×8.29×1/6.75=31.9KN/㎡则计算荷载P=31.9+12=43.9 kN/㎡2、立杆计算立杆受力的荷载：N=Pl2=43.9×0.9=39.51KN由于纵杆步距最大为l=1.2m,长细比λ=l/i=1200/15.78=76查表得φ=0.6758即[N]= ΦA[σ]=0.6758×489×215=71 505N=71.505KNN=39.51KN<[N]=71.505KN, 故立杆满足要求3、横梁松木条计算:横向方木：间距l1=900mm，跨径l2=600mm，规格4000×100×120mm横向方木单位荷载：g=Pl1=43.9×0.9=39.51KN/m跨中最大弯矩：Mmax =gl22/8=39.51×0.62/8=1.778 KN.m木条净截面抵抗矩Wji=bh2/6=0.1×0.122/6=2.4×10-4m3木条惯性矩: I=bh3/12=0.1×0.123/12=1.44×10-5m5顺纹弯应力验算：σw = Mmax/ Wji=1.778/2.4×10-4 =7408Kpa<[σw]=12000Kpa挠度验算:最大挠度:f max =5×gl24/384EI=5×39.51×0.64/(384×9×106×1.44×10-5)=0.51mmf max <l2/400=1.5mm故满足要求4、纵梁松木条计算：纵向方木：间距l1=350mm，跨径l2=900mm，规格4000×100×120mm方木单位荷载：g=Pl1=43.9×0.35=15.365KN/m跨中最大弯矩：Mmax =gl22/8=15.365×0.92/8=1.556KN.m木条净截面抵抗矩Wji=bh2/6=0.1×0.122/6=2.4×10-4m3 木条惯性矩: I=bh3/12=0.1×0.123/12=1.44×10-5m5顺纹弯应力验算：σw = Mmax/ Wji=1.556/2.4×10-4 =6483Kpa<[σw]=12000Kpa挠度验算:最大挠度:f max =5×gl24/384EI=5×15.365×0.94/(384×9×106×1.44×10-5)=1.01mmf max <l2/400=2.25mm故满足要求5、模板计算:模板采用赤杉黑模板，规格2440×1220×18mm，由于箱梁先施工完底板后再进行肋墙施工,故模板受力按箱梁底板24cm厚进行计算,计算跨径为纵梁木条跨径l=350mm，b=1220mm，h=18mm每米模板上荷载g=(26×0.24+12)×1.22=22.253 KN/m跨中弯矩：M1/2=gl2/8=22.253×0.352/8=0.341 KN.m按集中力P=1.5KN计算: M1/2=Pl/6=1.5×0.35/6=0.088 KN.m <0.341 KN.m故Mmax=0.341 KN.m模板净截面抵抗矩Wji=bh2/6=1.22×0.0182/6=6.588×10-5m3模板惯性矩: I=bh3/12=1.22×0.0183/12=5.929×10-7m5顺纹弯应力验算：σw = Mmax/ Wji=0.341/6.588×10-5 =5176Kpa<[σw]=13000Kpa挠度验算:最大挠度:fmax=5×gl4/384EI=5×22.253×0.354/(384×10×106×5.929×10-7)=0.7mmfmax<l/400=0.88mm故满足要求6、地基承载力要求立杆下托支撑在枕木上，枕木规格4000×100×150mm立杆承载荷载R=gl/2=43.9×0.9/2=19.755KN每根枕木上最多有立杆4/0.6=7根,故对地基承载力σ=7R/A=7×19.755/(4×0.15)=230Kpa支架的地基承载力要求大于230Kpa三、梁体实心段(墩轴两侧3m范围)以第7跨为算例,立杆横向间l1=60cm,纵向间距l2=60cm1、计算荷载砼输送泵出口砼冲击产生的荷载=4 kN/㎡振动器产生的垂直于模板的荷载=3kN/㎡施工人员及料具，胶合板，方木自重产生的荷载=5 KN/㎡梁体容重取γ=26 KN/m3，取1m长的箱梁计算，截面面积=20.12㎡，底面6.75m故梁体荷载=26×20.12×1/6.75=77.5KN/㎡则计算荷载P=77.5+12=89.5 kN/㎡2、立杆计算立杆受力的荷载：N=Pl2=89.5×0.6=53.7KN由于纵杆步距最大为l=1.2m,长细比λ=l/i=1200/15.78=76查表得φ=0.6758即[N]= ΦA[σ]=0.6758×489×215=71 505N=71.505KNN=53.7KN<[N]=71.505KN, 故立杆满足要求3、横梁松木条计算:横向方木：间距l1=600mm，跨径l2=600mm，规格4000×100×120mm横向方木单位荷载：g=Pl1=89.5×0.6=53.7KN/m跨中最大弯矩：Mmax =gl22/8=53.7×0.62/8=2.4165 KN.m木条净截面抵抗矩Wji=bh2/6=0.1×0.122/6=2.4×10-4m3 木条惯性矩: I=bh3/12=0.1×0.123/12=1.44×10-5m5顺纹弯应力验算：σw = Mmax/ Wji=2.4165/2.4×10-4 =10069Kpa<[σw]=12000Kpa挠度验算:最大挠度:f max =5×gl24/384EI=5×53.7×0.64/(384×9×106×1.44×10-5)=0.7mmf max <l2/400=1.5mm故满足要求4、纵梁松木条计算：纵向方木：间距l1=200mm，跨径l2=600mm，规格4000×100×120mm方木单位荷载：g=Pl1=89.5×0.2=17.9KN/m跨中最大弯矩：Mmax =gl22/8=17.9×0.62/8=0.8055KN.m木条净截面抵抗矩Wji=bh2/6=0.1×0.122/6=2.4×10-4m3 木条惯性矩: I=bh3/12=0.1×0.123/12=1.44×10-5m5顺纹弯应力验算：σw = Mmax/ Wji=0.8055/2.4×10-4 =3356Kpa<[σw]=12000Kpa挠度验算:最大挠度:f max =5×gl24/384EI=5×17.9×0.64/(384×9×106×1.44×10-5)=0.046mmf max <l2/400=1.5mm故满足要求5、模板计算:模板采用赤杉黑模板，规格2440×1220×18mm,计算跨径为纵梁木条跨径l=200mm，b=1220mm，h=18mm每米模板上荷载g=89.5×1.22=109.19 KN/m跨中弯矩：Mmax=gl2/8=109.19×0.22/8=0.546KN.m模板净截面抵抗矩Wji=bh2/6=1.22×0.0182/6=6.588×10-5m3模板惯性矩: I=bh3/12=1.22×0.0183/12=5.929×10-7m5顺纹弯应力验算：σw = Mmax/ Wji=0.546/6.588×10-5 =8288Kpa<[σw]=13000Kpa挠度验算:最大挠度:fmax=5×gl4/384EI=5×109.19×0.24/(384×10×106×5.929×10-7)=0.38mmfmax<l/400=0.50mm故满足要求6、地基承载力要求立杆下托支撑在枕木上，枕木规格4000×100×150mm立杆承载荷载R=gl/2=89.5×0.6/2=26.85KN每根枕木上最多有立杆4/0.6=7根,故对地基承载力σ=7R/A=7×26.85/(4×0.15)=313Kpa支架的地基承载力要求大于313Kpa一、有关力学参数1、贝雷桁梁单排单层贝雷梁容许弯矩M=788.2KN.m单排单层贝雷梁容许剪力Q=245.2KN贝雷片惯性矩I=250500cm4钢材弹性模量E=2.1×105Mpa2、松木材①、顺纹容许弯应力[σw]=12Mpa②、弹性模量E=9×103Mpa二、力学计算支架部分同第7跨施工,只对贝雷桁架梁进行验算,取双排贝雷梁进行受力分析，贝雷梁跨径l=9m,间距0.9m1、计算范围碗扣支架自重[4×14×7.5+（1.8×14+11.7×4）×6]×38.4=32716.8N=32.7KNq=43.9×0.9+(32.7+20.04)/9=45.37KN/m4、梁最大弯矩： Mmax =ql2/8=459.4KN.m< M=788.2KN.m梁最大剪力: Qmax = ql/2=204.2KN<Q=245.2KN梁最大挠度:fmax=5×ql4/384EI=7.4mm<l/400=22.5mm 因此贝雷桁架梁满足受力要求5、临时墩地基承载力要求临时墩断面尺寸1.2m×1m,计算长度取半幅施工跨河宽度24.3m 一个临时墩受力N=45.37×(24.3/0.9)×9×0.5=5512.5KNP=N/A=5512.5/(24.3×1.2)=189Kpa故要求临时墩地基承载力不小于189Kpa为了维持跨路的通行，在永连公路路肩和路中各浇筑宽80cm的砼基础埋设φ60cm的钢管桩作于支撑，钢管桩间距4m，顶面铺设双I28a的工字钢作为横梁，然后通过间距80cmI32a工字钢作为纵梁跨越公路，跨径4.8m,面木采用4000×100×120mm和4000×50×100双层松木条铺设,间距均35cm。