当前位置：文档之家 › 条件平差中必要观测数的确定

条件平差中必要观测数的确定

  • 格式：pdf
  • 大小：452.66 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

网平差中确定必要观测数的统一公式

网平差中确定必要观测数的统一公式

从该网确定不了任何一待定点的绝对高程 , 只能确定点间
的高差 , 即点间相对关系 。此时假设其中一点为已知点 , 然后确定其它四点的高程 , 所以必要观测数为 4。
以上是直观的分析 , 下面总结了适用于水准网确定必
要观测数的式子 , 公式如下 :
t = 1 ×m - 1 - c
(1)
其中 , m 为网中所有点数 (包括已知点和待定点 ) 。
模大且复杂时略显繁琐 , 所以总结了适用于确定测角网必
要观测数的公式 , 式子如下 :
t = 2 ×m - 4 - c
(2)
根据式 (2) 求图 2中各网的必要观测数 。图 2a中 , m
= 6 , μ = 4 , 由于 4个起算数据全是必要的起算数据 , 所
以
μ 1
=4,
得
c
=μ
-
μ 1
=0,
所以该网必要观测数为
则
μ 1
<μ≤ b , c
=μ
-
μ 1
;
④网中总起算数据数大于必要起算数据数 , 即
μ
>
b, 若 μ个起算数据中包含了
b个必要起算数据 ,
则
μ 1
=
b
<μ,
c
=μ -
b
=μ
-
μ 1
;
⑤当 μ > b时 , 若 μ个起算
数据中没有完全包含
b个必要起算数据 ,
则
μ 1
< b <μ,
c
=μ
-
μ 1
。
尽管以上五类情况各不相同 , 其计算多余起算数据数
下必要观测数 t确定的一些公式 。本文则对几种常见控制 网 (水准网 、测角网 、测边网 /边角网和 GPS网 ) 中确定必 要观测数进行分析 , 针对每种网分别总结出一个公式 , 然 后将这四类网的公式进行概括 , 最后得到各类网平差中确 定必要观测数的统一公式 。

高程控制网平差

高程控制网平差

i
i
i
h h V 改厕厕短的改正数， 代入上式，得：
i
i
i
V1 V2 V3 V4 W 0
W H A h1 h2 h3 h4 H B
1.附合水准路线的条件数和条件方程式组成
观测值5个，待定水准点2 个，所以条件有3个，可 以列出3个条件方程：
h1
H B h1 h2 H A 0
V 1 V 3 V 2 W a 0 V 2 V 4 V 6 W b 0 V 4 V 5 V 3 W c 0
(二)观测值权的确定：
1.各水准路线都进行了往返观测，每公里水准路线的观测中误差为 ，
则m：i
R mi2
1 4n
n i
2 i
i
式中，为测往返测高程不符值，以mm为单位；R为测段长度，以km为单位；n
H A h2 h3 h5 H D 0
H B h1 h3 h4 H C 0
一般以1个已知点为起点，其它已知点为终点，所构成的附合 水准路线为已知点数减1，这样可以列出的条件方程式为已知 水准点个数减1.
2.闭合水准路线的条件数和条件方程式的组成
从一个水准点出发，经过若干水准测段，又回到该 水准点，这样的水准路线称为闭合水准路线。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网，网中有4个待定点，没有已知点， 在平差计算时，只能确定个待定水准点之间的相互关系，如 果确定一个水准点的高程，就可以确定其他点的高程。因此， 该网的必要观测是3个，观测值总数是6个，又3个多余观测， 可以列出3个条件方程。为了让所列立的条件方程式互相独 立，没个条件方程都要求有一个其他方程没有用到的观测值， 即：

1-2条件平差原理--条件平差的计算步骤

1-2条件平差原理--条件平差的计算步骤

得： 3ka 9 0
3.步骤三
依据
K

N
W 1
aa
计算出联系数K。
解法方程得： ka 3
C
L3
L1
A
L2
B
三角形示例图
条件平差的计算步骤
4.步骤四
由式 V P 1 AT K 计算出观测值改正数，并依据式 Lˆ L V
出观测值的平差值。
计算
1 0 0 1

Lˆ3

L3
v3
731234
条件平差的计算步骤
5.步骤五
为了检查平差计算的正确性，将平差值待入平差值条件方程式 ALˆ A0 0 ，
看是否满足方程式关系。
583115 481611 731234 180 0
3
V P1AT K 0 1 0 1 3 3
0 0 1 1
3

Lˆ1 Lˆ2


L1

L2


v1 v2


583115 481611
条件平差的计算步骤
1.步骤一
根据实际问题，确定几何模型的总观测值的个数 n，必要观测值的个数 t 及
多余观测值的个数 r=n-t，进一步列出平差值条件方程 ALˆ A0 0 或改正数条 件方程 AV W 0 。
C
L3
L1
A
L2
B
三角形示例图
以确定三角形的形状为例，对三角形中的三个 内角等精度观测，得观测值如下： L1=58°31′12″，L2=48°16′08″，L3=73°12′31″，试用条 件平差法，计算三角形各内角的平差值。

测量平差问题中必要观测数的确定

测量平差问题中必要观测数的确定
分析 :示例 6 为一测角网 ,包含 2 个起算数据 ( α～ 1 , α～ 2 ) ,虽然起算数据个数不够 ,但仍然有多余 起算数据 ( α～ 1 , α～ 2 中只有 1 个是必要起算数据) , 属表中的 J 22 情形 ,此时需要额外假定 3 个起算数 据 (1 个点的坐标和 1 条边长) ,这样 ,全部起算数据 数 Q = 5 ,必要观测数为 t = 2 p - Q = 2 ×5 - 5 = 5 。
图 9 图 10
要额外假定 3 个起算数据 (1 个点的坐标和 1 个方 位角) ,属表中的 B 21 情形 ,必要观测数为 t = 2 p - 3 = 2 ×6 - 3 = 9 。
从以上示例分析可知 ,本文根据实际教学的经 验 ,总结出测量平差问题中不同观测条件 、不同图形 条件下的必要观测数确定的通用公式具有普遍适用 性 ,图表简洁清晰 。这对于更好地掌握测量平差的 基本理论和方法 ,正确应用平差模型具有很好的价 值 ,可以推广应用 。
推算定位 ,可以确保运动轨迹的完整性 。 5. GPSΠINS 惯性组合导航系统虽然精度高 ,但
由于价格昂贵而难以普及 ,而 GPSΠDR 组合系统中 可采用低成本的陀螺仪 ,一个在 1 000 元左右 ,里程 计可采用车辆自带车速传感器 ,所以 GPSΠDR 组合 系统具有成本低 、体积小的特点[1] , 容易大批量装 备。
参考文献 :
[1 ] 董绪荣. 一种低成本 GPS 组合导航定位系统 [J ] . 指挥 技术学院学报 ,2000 , (10) :728.
[2 ] 张相芬 ,袁 信. 自适应卡尔曼滤波在组合导航中的应 用[J ] . 舰船导航 ,2003 , (3) :34235.
(上接第 15 页) 已知方位角 , P1 , P2 为待定点 , S1 ～ S5 为观测边 。

测量平差问题中必要观测数的确定

测量平差问题中必要观测数的确定
3 2 1 4 5 6 7 4
n=15 t=3p-3=9
n=33 t=3p-3-3=15
1 3
2
P3
S0 为已知边, P1 , P2 ,P3 , P4 , P5 , P6 为待定点, ∠1～ ∠16 为观测角。 n=16 t = 2 p - 4 = 2 ×6 - 4 = 8
（2）当存在多余起算数据时
t=2p-4-q
A , B , C 为已知点, P1 ,P2 , P3 为 待定点, ∠1～ ∠12 为观测角。
n=12; t=2p-4-2=6。
~ 为已知方位角,P1 , P2 , P3 , P4 , P5 为待定点, ~ 2 1 ∠1～ ∠13 为观测角。
n=13; t=2p-4-1=5。
~ 为已知方位角, P1 , P2 , P3 , P4 , A , B 为已知点, 0 P5 , P6 为待定点, ∠1～∠21 为观测角。
n=5 t=2p-3-q=2×4-5=3
P1 , P2 , P3 , P4 , P5 , P6为待定点, S1～ S3 为观测边。
t = 2 p - 3= 2 ×6 - 3 = 9。

GPS网
a=3,b=3。
（1）当起算数据<=必要起算数据，且无多余起算 数据时 t=3p-3 （2）当存在多余起算数据时 t=3p-3-q

必要观测
为了确定观测对象的位置或形状、大小所必须的 最少观测数，称为必要观测。在测量中必要观测 是指为确定模型中所有待定点值（高程值或坐标 值）所需要的最少观测数。 必要观测数对参数个数的选择、多余观测数的确 定具有重要的意义。
必要观测数的确定
观测值个数：n； 必要观测数：t； 多余观测数：r； 所有点个数：p； 多余的起算数据：q； 确定每一个待定点值所需观测数：a； 必要起算数据个数（必要的起算基准）：b。

测量平差问题中必要观测数的确定

测量平差问题中必要观测数的确定

A ,B 为已知点, 为已~知0 方位角, P1 , P2 为待定点, S1～ S5 为观测边。
n=5
t=2p-3-q=2×4-5=3
P1 , P2 , P3 , P4 , P5 , P6为待定点, S1～ S3 为观测边。 t = 2 p - 3= 2 ×6 - 3 = 9。
GPS网
a = 3, b = 3 。
必要观测
为了确定观测对象的位置或形状、大小所必须的最少观测数，称 为必要观测。在测量中必要观测是指为确定模型中所有待定点值 （高程值或坐标值）所需要的最少观测数。
必要观测数对参数个数的选择、多余观测数的确定具有重要的意义 。
必要观测数的确定
观测值个数：n； 必要观测数：t； 多余观测数：r； 所有点个数：p； 多余的起算数据：q； 确定每一个待定点值所需观测数：a； 必要起算数据个数（必要的起算基准）：b。
A , B 为已知点, 为已~知0 方位角, P1 , P2 , P3 , P4 , P5 , P6 为待定点, ∠1～∠21 为观测角。
n=21
t = 2 p - 4-1 = 2 ×7 - 5 = 9
边角网/测边网
a=2；b=3
（1）当起算数据<=必要起算数据，且无多余起算数据时
t=2p-3
（2）当存在多余起算数据时 t=2p-3-q
测量平差问题中必要观测数的确定
基本概念
必要元素
起算数据 必要观测
必要元素
能够唯一确定一个几何模型所必要的元素
起算数据
必要的起算数据
பைடு நூலகம்
水准网
1
测角网
4
测边网/边角网
3
GPS网
3
说明

必要观测个数

必要观测个数

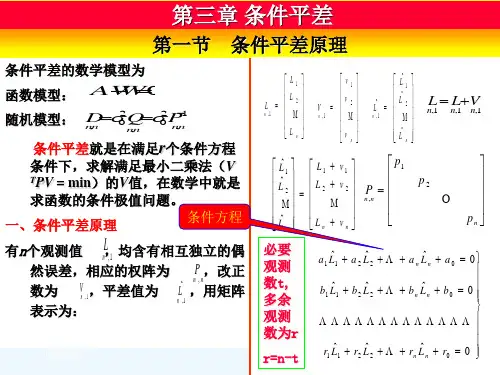
由条件平差原理知，多余观测数与条件方程数是相等的，有了多余观测数，也就确定出了条件方程的个数。

因此，问题的关键是判定必要观测数t。

1.网中有2个或2个以上已知点的情况三角网中有2个或2 个以上已知三角点，就一定具备了4个必要起算数据。

无论是测角网、测边网还是边角同测网，如果有2个已知点相邻，要确定一个未知点的坐标，需要观测两个观测值（2个角，或者1条边和1个角，或者2条边）。

也就是说，确定1个未知点要有2个必要观测值；那么如果网中有p个未知点，必要观测数应等于未知点个数的两倍。

t = 2 ·p(3-4-1)(1) 测角网图3-9所示，三角网中有2个已知点，待定点个数为p =6。

如果三角网中观测量全部是角度时。

总观测值个数：n = 23必要观测数：t = 2 · p =12则多余观测数，即条件平差条件方程个数：r = n – t = 11(2) 测边网在图3-9中，如果三角网中观测量全部是边的长度时：总观测值个数：n = 14必要观测数：t = 2 · p =12则多余观测数，即条件平差条件方程个数：r = n – t = 2(3) 边角同测网在图3-9中，如果三角网中的所有的角度值和所有的边长值都进行观测时：总观测值个数：n = 37必要观测数：t = 2 · p =12则多余观测数，即条件平差条件方程个数：r = n – t = 252. 网中已知点少于2个的情况有些情况下，三角网中已知点可能少于2个，只有1个已知点、1个已知边和1个已知方位角，或者没有已知点和已知方位角只有1个已知边。

但是，不管怎样说，1条已知边是必须已知的，或者需要进行观测的。

如果没有已知点，可以假定网中的1个未知点；如果没有已知方位角，可以取网中的1个方向的方位角为某一假定值。

这样也就间接地等价于网中有2个相邻点的坐标是已知的。

(1) 测角网三角网中共有p个三角点、1个已知方位角（也可以没有）、1个已知点（也可以没有已知点）和1个已知边长S（或者也是观测得到的），并观测了所有的角度。

高程控制网平差

高程控制网平差

1.单位权中误差的计算公式：
m0 ˆ0
PVV
r
2.每km高差中误差：
m m0
C
3.最弱点的高程中误差
最弱点是指误差最大的待定水准点，一般为离开已知水准点 最远的点。首先要列出最弱点的权函数式：
V F f 1V1 f 2V 2 f nV n
利用m f
1
m0式P计f 算最弱点高程中误差。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网，网中有4个待定点，没有已知点， 在平差计算时，只能确定个待定水准点之间的相互关系，如 果确定一个水准点的高程，就可以确定其他点的高程。因此， 该网的必要观测是3个，观测值总数是6个，又3个多余观测， 可以列出3个条件方程。为了让所列立的条件方程式互相独 立，没个条件方程都要求有一个其他方程没有用到的观测值， 即：
在水准网中，把3条或3条以 上水准路线的交点称为结点。 两条水准路线的交点称为节点。
（一）按间接平差法对结点进行平差
1.误差方程式的列立
不考虑水准路线中的节点，将水准路线的高差作为独立观测 值，取结点的近似高程改正数为未知数，列立每条水准路线 高差观测值的误差方程。
如图，路线高差观测值以表示，已知
（一）按间接平差法对结点进行平差
3.法方程式的解算 法方程式系数阵的逆阵为：
Q
N Q QQ 1
11
XX
21
31
Q 12
Q 22
Q 32
Q
13
Q Q23

测量平差原理

测量平差原理

间接平差： 选定t个独立的参数，将每个 观测值分别表示成这t个独立参数的函数， 组成观测方程，这种以观测方程为函数模 型的平差方法就是间接平差。
其数学模型为：
L B X d
n1 nt t1 n1
D
nn
2 0
Q
nn
P 2
1
0 nn
间接平差的数学模型
观测三角形内角，选择t=2个独立
参数A和B为平差参数，设为X1 、X2 则n=3个观测方程为：
针对偶然误差的测量平差中，利用最小二乘 法求得的估计量是最优估计量，具有以下性质：
（1）一致性；（2）无偏性；（3）有效性
数学模型 ：用数学关系描述几何模型的几何关系和内在 联系 。
函数模型 ：几何关系，描述观测量之间或观测量与待定 量之间的数学函数关系式 。
随机模型 ：内在联系，是描述观测量及其相互间的统计 相关性质。实际上，测量平差中所谓的随机模型，就是 观测值向量的权阵。
方程式不能由其他方程式线性组合得到） （3）形式简单
列方程依据：角度、边长、高差等几何关系
条件平差的函数模型举例 (1)
r=2
条件平差的函数模型举例 (2)
S1
1
A
C
已知点：A、B
观测值如图
3
S2
2 B
r=3
条件平差的函数模型举例 (3)
C
D
L3 L4
L6
已知点：A、B
L1
A
L2
L5
B
观测值： L1- L6
必要观测、多余观测
确定平面三角形的形状
观测三个内角的任意两个即可,称其必要
元素个数为2，必要元素有 C32种选择
确定平面三角形的形状与大小

第3章条件平差原理

第3章条件平差原理

v1 v2 v3 v4


573233

730305

1265125
1043317
推导如下：
VTPV VTP(P1ATK) VTATK(AV )TKWTK
纯量形式
20.09.2019 4
第三章 条件平差
第一节 条件平差原理
二、精度评定
则上述方程可表示为：
2. L、 W 、 K 、 V、 L ˆ的协因数阵及互 协因数阵
LL
W (A L A 0) A L A 0
DFFˆ02QFF
函数的方差
为了检查平差计算的正确性，可以将平差值代入平差值条件方程式，看是否满足 方程关系。
20.09.2019 10
第三章 条件平差
第一节 条件平差原理
[例3-1] n=4 t=3 r=1
A 1 P A TKW 0
p1
1

P
p2

1

n,n
Lˆ
n ,1


Lˆ Lˆ
1 2



Lˆ
n

L LV
n,1 n,1 n,1

Lˆ Lˆ
1 2



L1

பைடு நூலகம்
L
2


v1
v
2



Lˆ
n


L
n

vn

p1 P n,n
p2

kb


rr

论测量平差中必要观测数的确定

论测量平差中必要观测数的确定
1 计算必要观测数的新方法
控 制 测 量 的 目 的 ，就 是 要 确 定 控 制 网 中 未 知 点的坐标或（和）高 程 。为 此 ，控制网必须具有一 定 种 类 及 数 量 的 起 算 数 据 ，以 便 确 定 控 制 点 在 坐 标系统或高程系统中的位置。各种控制网的必 要起算数据如表1。
表 1 控制网必要起算数据的个数和种类
第一种情况：起 算 数 据 只 含 点 位 起 算 数 据 ，
不 含 非 点 位 起 算 数 据 。 由 前 述 讨 论 可 知 ，此时的
必要 观 测 数 〖 完全由未知点个数确定。显 然 ，于
水 准 网 的 必 要 观 测 数 〖 就 是 未 知 点 （高 程 ）的个
数 ；而平面控制网的必要观测数就是未知点坐标
和 控 制 网中 未知 点数 有关 外 ，还 与 起 算 数 据 及 其 种 类 有 关 。本 文 通 过 分 析 必 要 观 测 与 各 类 起 算 数 据 之 间 的 内
在 联 系 ，给出了确定必要观测数的一种新方法，并 列 举 了 不 同 种 类 的 控制网实例验证了该方法的正确性。与已有 方法相比，新方法推导思路简洁，容 易理解，且计算公式简单、便于记忆和使用，对测量平差教学有一定的帮助。
第 32卷 第 1 期
付 新 启 ：论 测 量 平 差 中 必 要 观 测 数 的 确 定
41
据 。满足要求后的起算数据可分为两类：一类是
点位起算数据，如坐标、高 程 等 ；另一类是非点位
起算数据，常 见 为 方 位 角 、边 长 等 ，也可以是高
差 。下面就起算数据的这两种情况来分别讨论
必要观测数〖 的计算方法。
[ 关 键 词 ] 控 制 网 ；测 量 平 差 ；必 要 观 测 ；必要起算数据

测量平差

测量平差

条件方程（一）、水准网1、水准网的分类及水准网的基准分为有已知点和无已知点两类。

要确定各点的高程，需要1个高程基准。

2.水准网中必要观测数t的确定有已知点：t等于待定点个数无已知点：t等于总点数减一3、水准网中条件方程的列立方法列条件方程的原则：1、足数； 2、独立；3、最简（1）、先列附合条件，再列闭合条件（2）、附合条件按测段少的路线列立，附合条件的个数等于已知点的个数减一（3）、闭合条件按小环列立（保证最简），一个水准网中有多少个小环，就列多少个闭合条件在水准网条件平差中，按以上方法列条件方程，一定能满足所列条件方程足数、独立、最简原则。

边角网条件方程单一附合导线的条件方程一个方位角条件两个坐标条件纵坐标条件为所以纵坐标条件方程为：纵坐标条件方程的最终形式为：GPS基线向量网三维无约束条件平差1.GPS基线向量网的观测值2、GPS基线向量网三维无约束平差的基准及必要观测数t3、GPS基线向量网三维无约束平差的条件方程的列立GIS数字化数据采集中，折角均为90°的N边形的条件方程直角条件：小结：一、条件平差及其目的二、条件平差的原理三、总结了条件平差的步骤（1）根据具体问题列条件方程式；（2）组成法方程式，（3）解法方程；（4）计算改正数V，（5）求观测值的平差值（6）检核（7）精度评定附有参数的条件平差小结1、为了某种需要，选择参数；2、每选一个参数，就增加一个条件方程，选择u 个参数，就增加u 个条件方程；3、条件方程的总数c=r+u ；4、单位权中误差的计算公式不变；5、求平差值函数的中误差时，应将平差值函数分别对观测值的平差值和参数求偏导数。

间接平差三、选取参数的个数和原则1、所选取t个待估参数必须相互独立；2、所选取t个待估参数与观测值的函数关系容易写出来。

四、不同情况下的误差方程1、水准网误差方程2、方位角误差方程测方位坐标平差函数模型测角网函数模型3、测边网误差方程4、GPS网误差方程。

测量平差中条件方程类型确定的分析

测量平差中条件方程类型确定的分析

测量平差中条件方程类型确定的分析作者：泥立丽王永来源：《商情》2020年第33期【摘要】给出了测量平差问题中各类条件方程的确定方法。

在测角三角网的平差中，正确无误地确定各类条件方程是一个难点问题。

文中通过精选的四个测角三角网，从如何确定几何模型的类型、如何确定布网的目的、如何确定起算数据以及如何确定必要观测数等几个方面，分步骤地进行了详细的分析，并给出了思路。

文中给出的方法，简单易行，不容易出错，适合于大多数的初学者和普通测量工作者。

【关键词】几何模型;起算数据;必要观测数;条件方程在测量平差的教学工作中，对于一个几何模型，当确定了必要观测数后，就可以确定多余观测数并依此列出各种条件方程了。

条件方程的类型非常多，包括图形条件、圆周条件、极条件以及坐标方位角条件等。

如何正确地列出相应的条件方程是学生学习的一个难点，本文中，作者结合教学的实际精选了四个测角三角网，并给出了一些分析思路。

1 算例如图1至图4所示，为四个测角三角网，求下列各测角三角网按条件平差时条件方程的总数及各类条件的个数，其中Pi为待定点，i为已知边，i为已知方位角，i取非负整数。

2 分析思路2.1大体分析思路（1）确定几何模型的类型即根据三角网的观测值来确定它是测角三角网、测边三角网还是边角网。

如图1至图4均为测角三角网。

（2）确定布设三角网的目的即布设三角网是为了确定网的形状还是待定点的坐标。

如图1中，其已知数据包括两个已知点坐标、一个已知方位角，可知该网是为了确定待定点的坐标;图2中，没有已知点，但包括两条已知边长，因此该网是为了确定形状和大小，由于大小固定的网是形状不变时的一种特例，因此该网的最终目的是为了确定形状。

图3中，没有已知点，仅包括一条已知边长和两个坐标方位角，因此该网是为了确定形状。

图4中，包括3个已知点，因此该网最终目的是为了确定待定点的坐标。

（3）判断已知数据是否为起算数据已知数据未必是起算数据。

在观测网中，为了实现布网的最终目的，已知数据是否起作用需要进行判断。

测量平差中必要观测数的确立

测量平差中必要观测数的确立

测量平差中必要观测数的确立发表时间：2019-05-23T11:22:33.057Z 来源：《防护工程》2019年第1期作者：王鸿燕1 曹学伟1 崔素芳1[导读] 本文讨论了各种情况下必要观测数的个数，并对各种情况下的必要观测数进行了归纳，使用起来很方便。

山东农业工程学院国土资源与测绘工程学院山东济南 250100摘要：测量平差中，为确定必要观测数，针对常见的四类控制网分别列出公式，最后作了归纳。

关键词：平差；必要观测；控制网Abstract：surveying adjustment, in order to determine the necessary number of observations, formulas for four kinds of common control networks are listed and summarized.Adjustment：necessary observation; control network.1引言测量平差是依据某种最优化准则，由一系列带有观测误差的测量数据，求定未知量的最佳估值及精度的理论和方法。

平差的函数模型有四类：条件平差模型、附有参数的条件平差函数模型、间接平差和附有限制条件的间接平差。

其中，除条件平差没设定参数外，其它模型均设定了参数，参数的个数与必要观测具有特定的关系，本文针对不同观测条件、不同图形条件下必要观测数的确定讨论一些公式。

2多余观测数的计算及必要观测数下面是对涉及的几个相关概念、文中的一些符号规定以及多余起算数据的计算问题做的说明和简析[1-5]。

必要观测元素和必要观测数：能够唯一确定一个几何模型所必要的元素，称为必要元素。

必要元素的个数称为必要观测个数或必要观测数，用t表示。

多余观测元素和多余观测数：从总观测元素中去掉必要观测元素后，剩下的观测元素称为多余观测元素或多余观测数据。

多余观测元素的个数，称为多余观测数，用r表示，且r=n-t。

条件平差中必要观测数的确定

条件平差中必要观测数的确定
在确定必要观测数之前，我们先要了解必要起算数据。在测角网，测边网， 测边角网中，以及水准网中都需要一定的起算数据，也就是已知数据。有这些已 知数据后就可以推算出其它待测点的在已知控制网下的数据。当起算数据不足的 时候虽然也能解算出各个观测值的平差值，但不能求得该网型中待测点在一定控 制网下的数据。例如，水准网中我们没有控制点，也可以算的高差观测值的平差
图2 图 2 中，题目给定了 3 个控制点，也就是有 6 个起算数据，大于测角网 4 个的必要起算数据，多于的起算数据为 2，所以 q=2。 图形中，观测数有 12 个，总点数有 6 个点，p=6，po=4，总边数有 11 条 边，所以 So=10。 必要观测数： t=2p-4-q=2*6-4-2 总条件方程个数： r=n-t=12-6=6； 图形条件： r 图=n-So=12-10=2;
图3 图 3 中，有两个已知点以及一个已知方位角，给定起算数据为 5 个，大于 必要起算数据 4 个，所以 q=5-4=1。而总观测角数目为 21 个，总点数为 7 个 点，所以 p=7，po=5，总边数为 14 条边，So=13。所以： t=2p-4-q=2*7-4-1=9； r=n-t=21-9=12； r 图=n-So=21-13=8;
能够唯一确定一个集合模型所必要的元素除可以任意或必须给定的元素之外其余的必要元素必须通过观察求得通过观测得到的必要元素称之为必要观测量
在条件平差函数模型的学习过程中，必要观测数的确定十分重要，必要观测 数是确定方程个数的基础，而知道方程个数是列条件方程式的前提。往往有很多 同学不能很好理解和掌握必要观测数的确定，在这里我将我所学习和收集的资料 进行汇总，供大家学习参考。
r 极=So- 2Po=13-2*5=3； r 余=r- r 图- r 极=12-8-3=1； 这多余出来的一个条件方程，就是多余的方位角条件。且我们看见在该图 形中间 17，18，19，20，21 这几个观测值构成了一个圆周角条件，因此图形条 件中一个是 8-1=7 个图形条件。 今天就到此为止，希望对大家有帮助。

测量平差问题中必要观测数的确定

测量平差问题中必要观测数的确定

n=5 t=2p-3-q=2×4-5=3
P1 , P2 , P3 , P4 , P5 , P6为待定点, S1～ S3 为观测边。
t = 2 p - 3= 2 ×6 - 3 = 9。

GPS网
a=3,b=3。
（1）当起算数据<=必要起算数据，且无多余起算 数据时 t=3p-3 （2）当存在多余起算数据时 t=3p-3-q

水准网
a=1;b=1
n=6 t=p-1=3
n=6 t=p-3=3
在经典平差中， 水准网中 有已知点：t等于待定点的个数 无已知点：t等于总点数减一

测角网
a=2；b=4
（1）当起算数据<=必要起算数据，且无多余起 算数据时 t=2p-4
P1 P2
A , B 为已知点, P1 , P2 ,P3 为待 定点, ∠1～ ∠13 为观测角。 n=13; t=2p-4=6。 A , B , C 为已知点, P1 ,P2 , P3 为 待定点, ∠1～ ∠12 为观测角。 n=12; t=2p-4=6。
n=21 t = 2 p - 4-1 = 2 ×7 - 5 = 9

边角网/测边网
a=2；b=3
（1）当起算数据<=必要起算数据，且无多余起算 数据时 t=2p-3 （2）当存在多余起算数据时 t=2p-3-q
~ 为已知方位角, P1 , P2 为待定点, A ,B 为已知点, 0 S1～ S5 为观测边。
P3
S0 为已知边, P1 , P2 ,P3 , P4 , P5 , P6 为待定点, ∠1～ ∠16 为观测角。 n=16 t = 2 p - 4 = 2 ×6 - 4 = 8
（2）当存在多余起算数据时

必要观测数确定（平差讲课用）

必要观测数确定（平差讲课用）

必要观测数确定（平差讲课⽤）测量平差中必要观测数的确定⽅法⼀、控制⽹必要起算数据概述1.控制⽹必要起算数据的要求：见下表。

控制⽹种类必要起算数据个数必要起算数据种类⽔准⽹测⾓⽹测边⽹/边⾓⽹/导线⽹143⼀点⾼程两点坐标或⼀点坐标、⼀边长和⼀边⽅位⾓⼀点坐标和⼀边⽅位⾓2.平差计算时控制⽹的起算数据必须满⾜要求也就是说，确定必要观测数t时，控制⽹的起算数据⼀定已经满⾜了要求。

满⾜要求的起算数据不仅种类满⾜要求，且其个数⼀定等于或⼤于其必要起算数据的个数。

起算数据满⾜要求有两种情况：⼀是控制⽹的起算数据本⾝就满⾜要求；另⼀是控制⽹的起算数据本⾝不满⾜要求，经假定或实测补⾜后满⾜要求。

补充的起算数据也视为已知。

⼆、控制⽹必要观测数的计算⽅法起算数据可分为两类：⼀类是点位起算数据，如坐标、⾼程等；另⼀类是⾮点位起算数据，常见为平⾯控制⽹中的⽅位⾓、边长等。

⽔准⽹中⽆此类起算数据。

下⾯分别就这两种情况来讨论必要观测数t的确定。

1.起算数据只含点位起算数据，不含⾮点位起算数据。

显然，⽔准⽹的必要观测数t就是此类未知点（⾼程）的个数；⽽平⾯控制⽹的必要观测数就是此类未知点坐标的个数，也即为点数的2倍。

若以P表⽰控制⽹中未知点的个数，则此种情况下必要观测数t的计算⽅法为⽔准⽹：t=P平⾯控制⽹：t=2P2.起算数据既含有点位起算数据，⼜包含⾮点位起算数据。

包含⾮点位起算数据只有平⾯控制⽹。

这类数据都对应着⼀条边——有两个端点。

根据该边与控制⽹的连接情况，⾮点位起算数据⼜分为两类：⼀类是两端点都包含在控制⽹内部，如图5中的S0、α1、α2，图7中的α0，图9中的α1等，称为第⼀类⾮点位起算数据。

另⼀类是⼀端与控制⽹相连，⼀端⾃由，该边好像悬挂于控制⽹上，⼀般为已知⽅位⾓，如图6中的α0，图9中的αA、αB、αC等，称为第⼆类⾮点位起算数据或悬挂边。

如果假设⾮点位起算数据未知，也即⽹中只有点位起算数据。

则可看出：第⼀类⾮点位起算数据与确定未知点坐标有关：确定未知点坐标需要测定⽅位⾓、距离。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图3 图 3 中，有两个已知点以及一个已知方位角，给定起算数据为 5 个，大于 必要起算数据 4 个，所以 q=5-4=1。而总观测角数目为 21 个，总点数为 7 个 点，所以 p=7，po=5，总边数为 14 条边，So=13。所以： t=2p-4-q=2*7-4-1=9； r=n-t=21-9=12； r 图=n-So=21-13=8;
在知道必要起算数据后，我们根据图形中提供的起算数据就可以分类讨论必 要起算数了。具体见下表：
必要观测数的确定就看上表。让我们先来看一个例题：
图1 上图中，是一个测角网，其中没有起算数据。总共观测了 16 个角度值，其 中这个几何图形中，一共有 6 个点，那么它的必要观测数 t=2p-4=12-4=8，多于 观测数 r=n-t=16-8=8 个。也就是说这个图形一共应该列出 8 个条件方程式。那 么这些条件方程式中，有几个图形条件，有几个极条件呢？ 回答上面的问题，也就是我们接下来要讲的，如何确定独立测角网和独立测 边网，以及独立测边角网中，条件方程式的不同种类。请注意，我用了三个独立， 什么是独立呢？独立就是该网的起算数据小于或等于该网的必要起算数据。例如 测角网的给定的起算数据小于或等于 4。测边网和测边角网给定起算数据小于或 等于 3。
在确定必要观测数之前，我们先要了解必要起算数据。在测角网，测边网， 测边角网中，以及水准网中都需要一定的起算数据，也就是已知数据。有这些已 知数据后就可以推算出其它待测点的在已知控制网下的数据。当起算数据不足的 时候虽然也能解算出各个观测值的平差值，但不能求得该网型中待测点在一定控 制网下的数据。例如，水准网中我们没有控制点，一个已知控制点了，我们就可 以推算出所有待求点的高程。
不同网型必要起算数据不同，见下表：
其中，水准网必要起算数据是 1 个，有一个点高程就可以推算出所有点的高 程。测角网，必要起算数据为 4，起算数据为 2 点坐标，即 2 对点的 x、y 就有 4 个起算数据了。或者一个点的坐标 x、y，以及一条边的边长 s，还有一个方位角 α。测边网和边角网相同，需要 3 个必要起算数据，就是 1 个点坐标 x、y，以及 一个方位角。
图2 图 2 中，题目给定了 3 个控制点，也就是有 6 个起算数据，大于测角网 4 个的必要起算数据，多于的起算数据为 2，所以 q=2。 图形中，观测数有 12 个，总点数有 6 个点，p=6，po=4，总边数有 11 条 边，所以 So=10。 必要观测数： t=2p-4-q=2*6-4-2 总条件方程个数： r=n-t=12-6=6； 图形条件： r 图=n-So=12-10=2;
极条件： r 极=So- 2Po=10-2*4=2； 多余条件方程个数： r 余=r- r 图- r 极=6-2-2=2； 这余下的 2 个条件是什么条件呢？其实我们看见多出了一个坐标，多的这 坐标就可以列出两个坐标条件。即是 B 点 x 与 y 坐标构成的坐标方程。 我们还看见这个图形中 P2 点构成了一个圆周条件，所以 2 个图形条件中有 一个是圆周条件。余下的图形条件为 2-1=1 个。 让我们再看一个例题：
上表中，n 为总观测数，t 为必要观测数，u 为所设参数个数，r 为多余观测 数，s 为约束条件方程个数。
从上表中可以看出，条件方程式的个数等于多于观测数的个数，而多于观测 数等于总观测数减去必要观测数。其中必要观测数是这样定义的：能够唯一确定 一个集合模型所必要的元素，除可以任意或必须给定的元素之外，其余的必要元 素必须通过观察求得，通过观测得到的必要元素称之为必要观测量。
r 极=So- 2Po=13-2*5=3； r 余=r- r 图- r 极=12-8-3=1； 这多余出来的一个条件方程，就是多余的方位角条件。且我们看见在该图 形中间 17，18，19，20，21 这几个观测值构成了一个圆周角条件，因此图形条 件中一个是 8-1=7 个图形条件。 今天就到此为止，希望对大家有帮助。
在条件平差函数模型的学习过程中，必要观测数的确定十分重要，必要观测 数是确定方程个数的基础，而知道方程个数是列条件方程式的前提。往往有很多 同学不能很好理解和掌握必要观测数的确定，在这里我将我所学习和收集的资料 进行汇总，供大家学习参考。
不同观测模型其必要观测数与所设参数以及方程个数之间关系，请见下表：
上表中 n 是总观测数，这里的 Po 是总点数减去 2，So 是总边数减去 1。 让我们继续看图 1，Po=6,So=10,n=16 其中我们知道有 8 个条件方程，那么 图形条件有 n-s=16-10=6 个图形条件，r-r 图=8-6=2，余下的就是极条件。 这里讨论了在独立网下的情况，若是给定的起算数据大于必要起算数据呢？ 我们看 2 个例题，大家请注意下列两个例题给定的起算数据均大于必要起算 数据，所以上表不能完全套用。