29.2 三视图(第二课时)
- 格式:doc
- 大小:55.50 KB
- 文档页数:4


安徽省太和县胡总中心学校导学案 九年级数学(上)胡总中心学校数学教研组 汤传光编制29.2三视图(第二课时)【学习目标】1、会画简单几何体的三视图。
2、通过具体活动,积累观察,体会立体图形的三视图与立体图形的密切关系。
【学习重点】会画简单几何体的三视图。
【学习难点】1.对三视图概念理解的升华。
2.正确画出实际生活中物体的三视图。
【学习过程】一、依标独学活动一1.圆柱对应的主视图是( )。
(A )(B )(C )(D )2.主视图、左视图、俯视图都是圆的几何体是( )。
(A )圆锥(B )圆柱 (C )球 (D )空心圆柱3.画出下列几何体的三视图题后小结:画一个立体图形的三视图时要注意什么?二、围标群学活动二画出如图所示的支架(一种小零件)的三视图. 支架的两个台阶的高度和宽度都是同一长度。
题后小结:画组合体的三视图时,构成组合体的各个部分的视图也要注意“ , , 。
”例3下图是一根钢管的直观图,画出它的三视图温馨提示:钢管有内外壁,从一定角度看它时,看不见内壁.为全面地反映立体图形的形状,画图时规定: 看得见部分的轮廓线画成实线,因被其他那分遮挡而看不见部分的轮廓线画成虚线.安徽省太和县胡总中心学校导学案 九年级数学(上)胡总中心学校数学教研组 汤传光编制题后小结:画钢管的主视图与俯视图时,分别是从两个方向观察钢管后画出来的,这时只能见到钢管 ,见不到 ,所以 画为虚线。
图中虚线与相邻实线的距离即钢管 ,它等于左视图中两圆 。
四、达标测评1. 画出下列几何体的三视图2. 画出下列几何体的三视图。
3.一个透明的玻璃正方体内镶嵌了一条铁丝(如图所示的粗线),请画出该正方体的三视图。
1. 如图,粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的三视图。
五、课后反思:。

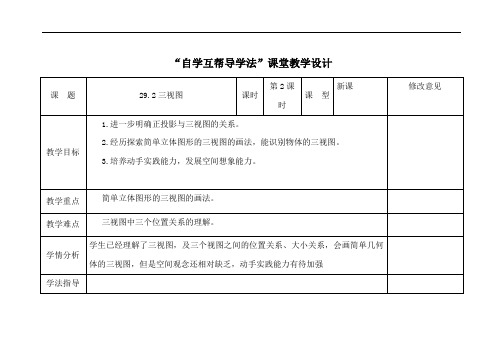
“自学互帮导学法”课堂教学设计课题29.2三视图课时第2课时课型新课修改意见教学目标1.进一步明确正投影与三视图的关系。
2.经历探索简单立体图形的三视图的画法,能识别物体的三视图。
3.培养动手实践能力,发展空间想象能力。
教学重点简单立体图形的三视图的画法。
教学难点三视图中三个位置关系的理解。
学情分析学生已经理解了三视图,及三个视图之间的位置关系、大小关系,会画简单几何体的三视图,但是空间观念还相对缺乏,动手实践能力有待加强学法指导教学过程教学内容[.Com]教师活动学生活动效果预测(可能出现的问题)补救措施修改意见一、复习巩固1.画一个立体图形的三视图时要注意什么?2.说一说:直三棱柱、圆柱、圆锥、球的三视图3、一个长、宽、高分别为 3,4,5 的长方体,如图所示,画它的三视图的步骤是什么?它的三视图显然都是长方形,主视图、俯视图、左视图长和宽各是多少呢?画法规则是什么?教师提问教师出示问题教师点评学生思考并回答学生思考,回答1、[.Com]2、……二、实例解析组合体三视图的画法画出如图所示干电池的三视图.三、交流合作,展示作品画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.1、教师提问:图中简单组合体可以看作由哪些基本几何体组成的?它们之间的位置关系是什么?2、引导学生画出三视图3、教师点评,并板演画图4、说说这个三视图与上节课所画三视图的不同之处教师提问:这个组合体是由哪些基本几何体组成?教师板演该组合体的三视图,口述画组合体三视图的法则,并提示学生注意这两个长方体的上下、前后位置关系.教师点评师生共同小结画图法则学生思考,讨论交流,展示结论学生尝试画图,小组交流,班级展示学生思考,回答学生思考并回答学生观察,体会画法学生独立练习,展示结果,学生互评[.Com]四、应用新知,巩固练习习题 29.2第 1 题.习题 29.2第 6 题(1).五、反思与小结画组合体三视图要遵循的法则六、布置作业习题 29.2第 6 题(2);习题 29.2 第 7 题………………学生容易受物体颜色的影响……教学反思。


29.2 三视图
第二课时
一、教学目标
1.学会根据物体的三视图描述几何体的基本形状或实物原型.
2.经历探究简单的几何体的三视图的还原,进一步发展空间想象能力,明白知识来源于实践,观察是得到知识的重要途径的道理.
3.经历从不同方向观察物体的活动过程,发展空间观念,能在与他人交流的过程中合理清晰地表达自己的思维过程.通过创设问题情境,让学生主动参与,激发学生的学习热情和兴趣,激活学生的思维.
二、教学重难点
重点:根据物体的三视图描述出几何体的基本形状或实物原型.
难点:根据物体的三视图想象几何体的形状或实物原型的形状并进行相关的计算.
教学过程(教学案)
一、问题引入
师提问:前面我们讨论了由立体图形(实物)画出三视图,那么由三视图是否也能想象出立体图形(实物)呢?
引导学生结合以下几个例子的三视图想象一下构造还原过程.
二、互动新授
(一)根据三视图判断立体图形
多媒体出示:
例3】如教材图29.2-8,分别根据三视图(1)(2),说出立体图形的名称.
(1)(2)
教材图29.2-8
【例4】根据物体的三视图(教材图29.2-10),描述物体的形状.
教材图29.2-10
学生分析、讨论后,得出结论。
教师多媒体出示答案,并总结:由三视图想象立体图形时,首先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后综合起来考虑整体图形(二)根据三视图计算立体图形的面积
【例5】某工厂要加工一批密封罐,设计者给出了密封罐的三视图(教材图29.2-12).请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
教材图29.2-12
学生练习后,小组交流、讨论.
【分析】对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际生产中,三视图和展开图往往结合在一起使用.解题思路是,先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积.教师多媒体出示解答过程(教材P100).
三、课堂小结
通过本节课的学习,你有什么收获?
四、板书设计
29.2三视图
第二课时
1.由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后综合起来考虑整体图形.
2.对于某些立体图形,沿着其中一些线剪开,可以把立体图形的表面展开成一个平面图形——展开图.
五、教学反思
在课堂教学中,应做好以下几个环节:
一、借助多媒体,设置情境,提高学生学习的积极性和兴趣,为学生合作交流探究做好准备.
二、由易到难,由熟悉的几何体(如长方体)的三视图观察、思考、概括总结出一般性结
论.
三、合作交流探究简单几何体的三视图的画法,及时加以总结.
四、学以致用,应用三视图相关知识解决基本问题.还原空间几何体,计算其表面积和体积.本节课的主要任务是引导学生由三视图还原出立体几何图形,故设计的思考题不能太难.上好本节课教学时间不宜控制,应抓住重点、难点,完成基本教学任务后,再发散与拓展,延续思考与研究.本节课视学生掌握情况,也可分为2课时完成.
导学方案
一、学法点津
学生由三视图确定立体图形的名称和形状就像编织一个花篮,由俯视图编织花篮的底面,且确定侧面的数量;由主视图和左视图确定前面的高度和侧面的高度、宽度;再由实线和虚线确定最后的位置.按照上述方法可以基本确定该立体图形的形状和名称,注意有时答案不是唯一的.
二、学点归纳总结
1.知识要点总结
由三视图想象立体图形时,首先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后综合起来考虑整体图形.
2.规律方法总结
(1)由三视图确定物体的形状可以直接由视图的形状确定,也可以采用检验的办法.(2)由三视图判断物体的形状:综合三个视图进行判断.
(3)物体的三视图不仅反映出物体的形状,而且也能反映物体的长、宽、高及各部分的长度,所以可以根据这些数据求出该物体的体积或表面积.
第二课时作业设计
1.如图(1)所示,是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是( ).
A.6 B.7 C.8 D.9
2.5个棱长为1厘米的正方体组成如图(2)所示的几何体.
(1)该几何体的体积是__________(立方厘米);(2)表面积是__________(平方厘米).
3.如图(3)是物体的俯视图,是一个等腰直角三角形,如图(4)是该物体的主视图,它是一个正方形,请根据这个物体的两种视图求出它的表面积和体积.
图(1)图(2)图(3)
图(4)
【参考答案】
1.A 2.(1)5 (2)22
3.解:由俯视图和主视图可知这个物体是底面为等腰直角三角形的直棱柱.由已知得
等腰直角三角形的直角边为102cm ,∴表面积S =2×(102)2+20×102+12
×(102)2×2=(600+2002)(cm 2),体积V =12
×(102)2×102=10002(cm 3).。