第二课时29.2三视图-第二十九章投影和视图
- 格式:ppt
- 大小:2.15 MB
- 文档页数:38



第二十九章投影与视图29.1投影(1)学习目标1、经历实践探索,了解投影、投影面、平行投影和中心投影的概念;2、了角平行投影和中心投影的区别。
3、使学生学会关注生活中有关投影的数学问题,提高数学的应用意识。
学习重点理解平行投影和中心投影的特征;学习难点在投影面上画出平面图形的平行投影或中心投影。
教学互动设计备注(一)创设情境你看过皮影戏吗?皮影戏又名“灯影子”,是我国民间一种古老而奇特的戏曲艺术,在关中地区很为流行。
皮影戏演出简便,表演领域广阔,演技细腻,活跃于广大农村,深受农民的欢迎。
(二)你知道吗北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.问题:那什么是投影呢?出示投影让学生感受在日常生活中的一些投影现象。
一般地.用光线照射物体.在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面.有时光线是一组互相平行的射线.例如太阳光或探照灯光的一束光中的光线(如图).由平行光线形成的投影是平行投影.例如.物体在太阳光的照射下形成的影子(简称日影)就是平行投影.由同一点(点光源)发出的光线形成的投影叫做中心投影.例如.物体在灯泡发出的光照射下形成影子就是中心投影.(三)问题探究(在课前布置,以数学学习小组为单位)探究平行投影和中心投影和性质和区别1、以数学习小组为单位,观察在太阳光线下,木杆和三角形纸板在地面的投影。
2、不断改变木杆和三角形纸板的位置,什么时候木杆的影子成为一点,三角形纸板的影子是一条线段?当木杆的影子与木杆长度相等时,你发现木杆在什么位置?三角形纸板在什么位置时,它的影子恰好与三角形纸板成为全等图形?还有其他情况吗?(四)应用新知:(1)地面上直立一根标杆AB如图,杆长为2cm。

描述:例题:初三数学下册(人教版)知识点总结含同步练习题及答案第二十九章 投影与视图 29.2 三视图一、学习任务1. 掌握常见物体的三视图的画法及其作用.二、知识清单三视图三、知识讲解1.三视图三视图定义将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓绘制出来的平面图形称为视图.从物体的前面向后面投射所得的视图称主视图;从物体的上面向下面投射所得的视图称俯视图;从物体的左面向右面投射所得的视图称左视图;三视图就是主视图、俯视图、左视图的总称.常见几何体的三视图 由视图到立体图形① 主视图反映物体的长和高,主要提供正面的形状;② 左视图反映物体的高和宽,主要提供左侧面的形状;③ 俯视图反映物体的长和宽,主要提供上面的形状,由俯视图看不出物体的高.下列几何体,主视图和俯视图都为矩形的是( )四、课后作业(查看更多本章节同步练习题,请到快乐学)解:D.如图是由个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )解:B.6如图是某个几何体的三视图,则该几何体的形状是( )A. 长方体B. 圆锥C. 圆柱D. 三棱柱解:D.根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.答案:1.某几何体的三视图如图所示,则这个几何体是A .圆柱B .正方体C .球D .圆锥D()解析:由主视图和左视图都是三角形可知,这个几何体是圆锥.答案:2.如图是由六个小正方体组合而成的一个立体图形,它的主视图是A.B .C.D .B()3. 将如图所示的绕直角边 旋转一周,所得几何体的左视图是A .B.C .Rt△ABC BC ()高考不提分,赔付1万元,关注快乐学了解详情。
答案:D .A答案:解析:4.如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是A.B .C .D .D此类题主要考查学生们的空间想象能力,一般考查常见的简单的几何体有圆柱,正方体及其组合体.应注意看的见的轮廓线与看不见的轮廓线的画法与圆锥与圆柱的视图的区别是否有圆心,相对来说考查的较为简单,此题故选D .()。

第二十九章投影与视图29.2 三视图课程标准课标解读1.会画直棱柱、圆柱、圆锥、球的主视图、左视图、俯视图,能判断简单物体的视图,并会根据视图描述简单的几何体。
2.了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作模型。
3.通过实例,了解上述视图与展开图在现实生活中的应用。
理解和掌握三视图的基本概念,能够画出棱柱、圆柱、圆锥、球的主视图,能够正确判断简单物体的三视图。
知识点01 三视图1.三视图有关的概念(1)视图:从某一方向观察一个物体时,所看到的平面图形叫作物体的一个视图。
(2)三视图:从3个互相垂直的方向观察物体,在正面内得到的由前向后观察物体的视图,叫作主视图;在水平面内得到的由上向下观察物体的视图,叫作俯视图;在侧面内得到的由左向右观察物体的视图,叫作左视图。
【微点拨】(1)视图的本质就是正投影;物体的主视图,等同于一束平行光线自物体的前方向后方照射,在正面投影面上得到的正投影;俯视图、左视图类似。
(2)三视图中的各视图,分别从不同方向表示物体的形状,三者结合能够较全面地反映物体的形状.2. 三视图之间的关系三视图的摆放一般是,主视图在左上方,它下方应是俯视图,左视图在右边.在物体的三视图中,主视图可反映出物体的长和高,俯视图可反映出物体的长和宽,左视图可反映出物体的高和宽.【微点拨】三视图中,主视图与俯视图表示同一物体的长;主视图与左视图表示同一物体的高;左视图与俯视图表示同一物体的宽.【即学即练1】如图所示的几何体,其主视图是()A .B .C .D .【答案】A 【分析】从正面看所得到的图形即为主视图,据此求解即可.【详解】解:从正面看看到的是一个长方形,中间有两条竖着的虚线,即,故选A 知识点02 画三视图1.画几何体的三视图画一个几何体的三视图时,先观察几何体,判断出从3个方向看几何体得到的平面图形,即三视图;然后把三视图按照一定位置画出来。
画三视图时,一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,被其他部分遮挡而看不见的画成虚线,不能漏掉。



第二十九章投影与视图29.2 三视图1.三视图的有关概念(1)当我们从某一角度观察一个物体时,所看到的图象叫做物体的一个__________.(2)一个物体在三个投影面内同时进行正投影,在正面得到的由前向后观察物体的视图,叫做__________;在水平面内得到由上向下观察物体的视图,叫做__________;在侧面内得到由左向右观察物体的视图,叫做__________.(3)常见几何体的三视图2.三视图的特征及画法(1)画三视图要注意三要素:主视图与俯视图长度相等;主视图与左视图高度相等;左视图与俯视图宽度相等.简记为“主俯长对正,主左高平齐,左俯宽相等”.(2)注意实线与虚线的区别:能看到的线用实线,看不到的线用虚线.3.根据三视图描述物体原来的形状及计算展开图的面积由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左面,然后综合起来考虑几何体的形状.再根据“长对正、高平齐、宽相等”的关系,确定轮廓线的位置以及各个方向的尺寸.观察三视图,并综合考虑各视图所表示的意义以及各视图间的联系,可以想象出三视图所表示的立体图形的形状,这是由视图转化为立体图形的过程.由立体图形可以确定三视图和展开图,立体图形的三视图和展开图是平面图形,立体图形、三视图和展开图中,三者知其一,我们就能确定另外两种图形,即三者之间可以互相转化.参考答案:1.(1)视图;(2)主视图;俯视图;左视图一、物体的三视图三视图中的各视图,分别从不同方面表示物体的形状,三者合起来能够较全面地反映物体的形状,单独一个视图难以全面地反映物体的形状,在实际生活中常用三视图描述物体的形状.二、根据三视图确定几何体1.由三视图想象立体图时,要先分别根据主视图、俯视图和左视图想象立体图的前面、上面和左侧面,然后再综合起来考虑整体图形.2.从实线和虚线想象几何体看得见和看不见的部分的轮廓线.三、由视图确定几何体的表面积和体积某些立体图可沿其中一些线剪开成一个平面展开图,在实际生产中,常将立体图、三视图和平面展开图相结合进行相关运算.。
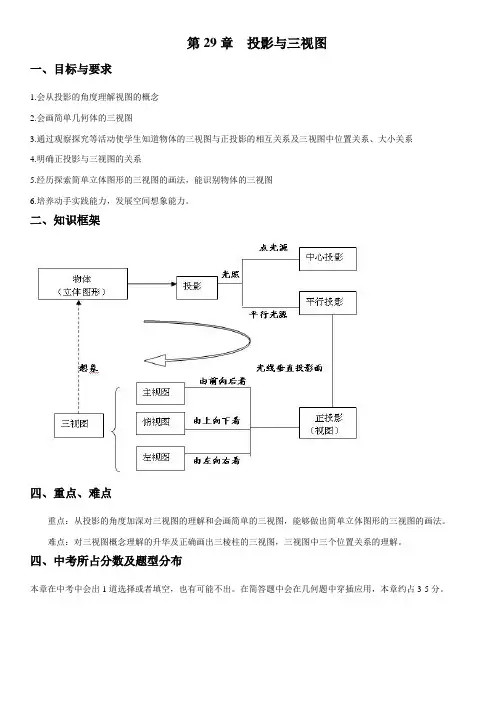
第29章投影与三视图一、目标与要求1.会从投影的角度理解视图的概念2.会画简单几何体的三视图3.通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系4.明确正投影与三视图的关系5.经历探索简单立体图形的三视图的画法,能识别物体的三视图6.培养动手实践能力,发展空间想象能力。
二、知识框架四、重点、难点重点:从投影的角度加深对三视图的理解和会画简单的三视图,能够做出简单立体图形的三视图的画法。
难点:对三视图概念理解的升华及正确画出三棱柱的三视图,三视图中三个位置关系的理解。
四、中考所占分数及题型分布本章在中考中会出1道选择或者填空,也有可能不出。
在简答题中会在几何题中穿插应用,本章约占3-5分。
第29章 投影与三视图29.1 投影1.投影:用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面。
2.平行投影:有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线。
由平行光线形成的投影是平行投影.3.中心投影:由同一点(点光源发出的光线)形成的投影叫做中心投影。
4.正投影:投影线垂直于投影面产生的投影叫做正投影。
例.把一根直的细铁丝(记为线段AB)放在三个不同位置:(1)铁丝平行于投影面;(2)铁丝倾斜于投影面;(3)铁丝垂直于投影面(铁丝不一定要与投影面有公共点).三种情形下铁丝的正投影各是什么形状?通过观察、测量可知:(1)当线段AB 平行于投影面P 时,它的正投影是线段11A B ,线段与它的投影的大小关系为11AB A B =;(2)当线段AB 倾斜于投影面P 时,它的正投影是线段22A B ,线段与它的投影的大小关系为22AB A B =;(3)当线段AB 垂直于投影面P 时,它的正投影是一个点3A .例.把一正方形硬纸板P (记正方形ABCD )放在三个不同位置:(1)纸板平行于投影面;(2)纸板倾斜于投影面;(3)纸板垂直于投影面。