子午线收敛角的计算之令狐文艳创作
- 格式:doc
- 大小:85.50 KB
- 文档页数:5

子午线收敛角的计算子午线收敛角的计算探讨摘要:利用给定的高斯坐标值(x,y)可以通过公式2,3得到其大地经纬度(B,L),得到(B,L)经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。
关键字:子午线坐标正算(反算)大地坐标投影长度比引言:为了求取子午线收敛角,我们可以有多种方法。
我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{(x,y)—>(B,L)},然后利用L,B就可以求取子午线收敛角。
在测量工作中,经常需要进行正算、反算、换带和子午线收敛角的计算工作。
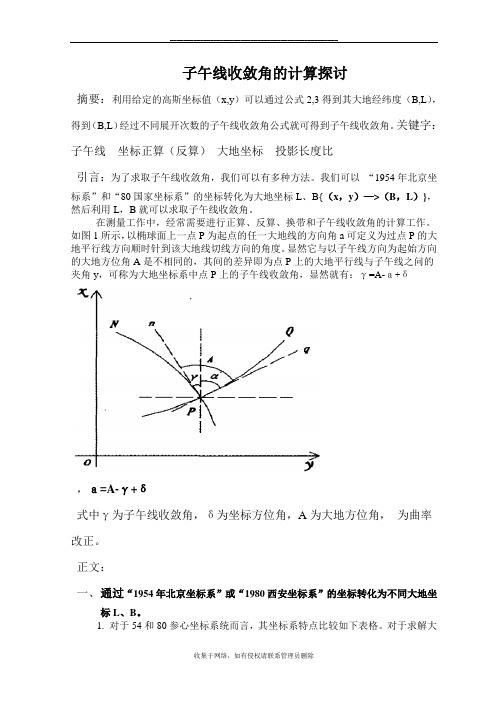
如图1所示,以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。
显然它与以子午线方向为起始方向的大地方位角A是不相同的,其间的差异即为点P上的大地平行线与子午线之问的夹角y,可称为大地坐标系中点P上的子午线收敛角,显然就有:γ=A-a+δ,a=A-γ+δ式中γ为子午线收敛角,δ为坐标方位角,A为大地方位角,为曲率改正。
正文:一、通过“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不同大地坐标L、B。
1. 对于54和80参心坐标系统而言,其坐标系特点比较如下表格。
对于求解大地纬度B,大地经度L需要迭代计算,可以用以下公式直接编写程序求解L、B,理论计算结果2,数值结果2: (2) (3)式中,X为由赤道至纬度B的子午线弧长,为计算点P点与中央子午线的经差。
N为卯酉圈曲率半径,t=tanB,η=e′cosB。
L-L0若以度为单位,则ρ=57.295779513;L-L0若以分为单位,则ρ=3437.7467708;L-L0若以秒为单位,则ρ=206264.80625。
上式中,我们利用(x,y)就可以得到(B,L)54年北京坐标系克拉索夫斯基椭球;参心坐标系长半轴a=6378245m;短半轴扁率α=1:298.3。
大地原点在原苏联的普尔科沃采用多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳;参心坐标系长半轴a=637814m;短半轴b=6356755.29m;扁率α=1:298.257;大地原点在陕西省泾阳县永乐镇;椭球短轴平行于地球地轴起始子午面平行于格林威治天文台平均子午面二、利用B、L进行高斯投影平面的坐标的计算的变形分析。
子午线收敛角的计算探讨摘要:利用给定的高斯坐标值(x,y)可以通过公式2,3得到其大地经纬度(B,L),得到(B,L)经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。
关键字:子午线坐标正算(反算)大地坐标投影长度比引言:为了求取子午线收敛角,我们可以有多种方法。
我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{(x,y)—>(B,L)},然后利用L,B就可以求取子午线收敛角。
在测量工作中,经常需要进行正算、反算、换带和子午线收敛角的计算工作。
如图1所示,以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。
显然它与以子午线方向为起始方向的大地方位角A是不相同的,其间的差异即为点P上的大地平行线与子午线之问的夹角y,可称为大地坐标系中点P上的子午线收敛角,显然就有:γ=A-a+δ,a=A-γ+δ式中γ为子午线收敛角,δ为坐标方位角,A为大地方位角,为曲率改正。
正文:一、通过“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不同大地坐标L、B。
1. 对于54和80参心坐标系统而言,其坐标系特点比较如下表格。
对于求解大地纬度B,大地经度L需要迭代计算,可以用以下公式直接编写程序求解L、B,理论计算结果2,数值结果2: (2) (3)式中,X为由赤道至纬度B的子午线弧长,为计算点P点与中央子午线的经差。
N为卯酉圈曲率半径,t=tanB,η=e′cosB。
L-L0若以度为单位,则ρ=57.295779513;L-L0若以分为单位,则ρ=3437.7467708;L-L0若以秒为单位,则ρ=206264.80625。
上式中,我们利用(x,y)就可以得到(B,L)54年北京坐标系克拉索夫斯基椭球;参心坐标系长半轴a=6378245m;短半轴扁率α=1:298.3。
大地原点在原苏联的普尔科沃采用多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳;参心坐标系长半轴a=637814m;短半轴b=6356755.29m;扁率α=1:298.257;大地原点在陕西省泾阳县永乐镇;椭球短轴平行于地球地轴起始子午面平行于格林威治天文台平均子午面二、利用B、L进行高斯投影平面的坐标的计算的变形分析。


子午线收敛角磁偏角
子午线收敛角是指地球椭球体面上一点的真子午线与位于此点所在的投影带的中央子午线之间的夹角,而磁偏角是指磁场强度矢量的水平投影与正北方向之间的夹角,即磁子午线与真子午线之间的夹角。
磁场强度矢量是指在一个特定点上的磁场中的磁场强度的方向和强度表示。
磁场强度矢量是一个有向矢量,用B表示,Bx、By、Bz分别表示磁场强度矢量B在X、Y、Z坐标轴的分量,i、j、k分别表示X、Y、Z坐标轴的单位矢量,有向量B的模B=(BxBx+ByBy+Bz*Bz)1/2,表示磁场强度的大小。

子午线收敛角计算公式及计算精度分析以《子午线收敛角计算公式及计算精度分析》为标题,本文将对子午线收敛角的定义、物理意义和计算公式进行详细分析,并对子午线收敛角计算的精度做出评估。
子午线收敛角是一种定义在空间曲率理论上的角度,它描述在一个曲率空间中两个不同子午线之间角度的变化情况。
它被用来描述万有引力场的形状,如地球表面的地貌等。
子午线收敛角是非常重要的度量,具有重要的物理意义。
子午线收敛角的计算公式可以从拉格朗日系数表示法中推出:$$ phi= frac{1}{2} sum_{i=1}^{3} (gamma_{ii} - gamma_{jj}) cdot Delta theta_{ij} $$其中,$gamma_{ij}$表示拉格朗日系数; $Delta theta_{ij}$表示两个子午线之间的夹角。
这里要计算子午线收敛角可以使用上述公式。
此公式计算结果对于子午线收敛角的精度有一定要求,如果计算结果误差大,会对实际应用造成影响。
为了评估子午线收敛角的计算精度,一种常用的方法是使用仿真数据。
在仿真实验中,通过改变空间曲率参数,产生不同子午线收敛角的情况,从而获得理想的测量结果。
用这些理想结果与计算结果比较,就可以评估子午线收敛角计算的精度了。
此外,为了提高子午线收敛角计算精度,还可以使用多种数值计算方法,比如拉格朗日元法、二阶中心差分法等。
这些方法都可以得到更精确的子午线收敛角计算结果,可以提供更准确的计算结果以满足应用需求。
综上所述,子午线收敛角是一种定义在空间曲率理论上的角度,可以用来描述万有引力场的形状,具有重要的物理意义。
计算子午线收敛角可以使用拉格朗日系数表示法中推导出的公式。
为了评估子午线收敛角计算的精度,可以使用仿真数据,也可以使用多种数值计算方法来提高计算精度。
本文根据子午线收敛角的定义、物理意义和计算公式,以及计算精度,对子午线收敛角做出了全面分析。

真子午线与中央子午线的收敛角真子午线与中央子午线的收敛角其实是测量地球表面上两条纵向线之间的角度,它们的区别在于位置不同。
真子午线是指贯穿地球北极和南极的线,也就是地球表面上的0度经线;而中央子午线则是指某个特定区域内经度为中心的经线。
在测量中,真子午线与中央子午线的收敛角是非常重要的参考参数。
此处,我们将从以下四个方面来探讨真子午线与中央子午线的收敛角:一、概念定义真子午线收敛角与中央子午线收敛角都是指地球表面上两条经线(纵向线)之间的角度。
其中,真子午线收敛角是指两条经线穿过地球两极的情况下的角度,而中央子午线收敛角则是指任意两条经线之间的角度。
二、计算方法真子午线收敛角和中央子午线收敛角的计算方法是不同的。
计算真子午线收敛角时,需要考虑地球的椭球形状,以及两条经线间的距离。
而计算中央子午线收敛角时,则只需要考虑两条经线之间的距离。
三、影响因素真子午线与中央子午线的收敛角都受到多种因素的影响。
其中,地理位置、对地面的曲率半径、大气密度、温度等因素都会对收敛角产生一定的影响。
由于真子午线跨越了整个地球,因此受到的影响也更加复杂和多样。
四、实际应用真子午线与中央子午线的收敛角在实际应用中也有较为广泛的应用。
例如,对于地图绘制和GPS导航等场景,在计算距离和方位角时都需要考虑真子午线与中央子午线的收敛角,以获得更为准确的结果。
综述以上四点,真子午线与中央子午线的收敛角是测量地球表面上两条纵向线之间的角度,它们的计算方法、影响因素以及在实际应用中的重要性都各有不同。
对于地理信息、航海、测量等领域的专业人士来说,熟练掌握真子午线与中央子午线的收敛角是十分必要的。
子午线收敛角计算公式及计算精度分析子午线收敛角是测量我们在地球上的位置的方法之一。
然而,它的计算精度至关重要,因为它是一种3D投影的基础。
因此,本文的主要目的是探讨子午线收敛角的计算公式和精度,以及如何减少计算的错误。
一、子午线收敛角的定义子午线收敛角是地图学上的一项基本概念,它指的是把地球上的一点线性投射到地图上时,投射端点与子午线之间的夹角。
子午线是地球上经度方向上的一条线,与地球赤道平行,地球上每一点的子午线都不同。
子午线收敛角用θ(θ <90°)表示,其计算公式为:θ=arccos(cosφ1cosφ2sin(λ2-λ1)+sinφ1sinφ2)其中,λ和φ是投影点的经度和纬度。
二、子午线收敛角的计算精度计算子午线收敛角的精度主要取决于地球模型的精度,它是空间位置信息计算的基础。
如果地球模型精度低,会影响子午线收敛角计算的精度,甚至产生误差。
例如,在地球表面变形较重的地区,如山区,可能会产生较大的误差。
实际计算过程中,计算机还会对数字的计算和精度有一定的影响。
例如,在电脑上使用浮点精度(float),这种计算精度远远不及双精度(double),因此会出现精度丢失的情况。
三、如何减少计算误差以上是子午线收敛角的计算公式和精度分析,下面我们来讨论如何减少计算误差。
首先,对地球模型进行精确测量,以减少误差。
其次,有必要采用更高精度的计算方式,例如双精度计算法,减少计算误差。
再者,可以使用更精确的坐标系统,例如WGS84,准确计算子午线收敛角。
此外,在计算过程中使用合适的中间计算空间,例如椭球面,有助于计算子午线收敛角的精度。
本文简要介绍了子午线收敛角的计算公式及其计算精度分析,以及如何减少计算误差的方法。
通过有效的采用更精准的计算方法,选择更好的投影体系,以及使用适合的计算空间,可以有效提高子午线收敛角的计算精度,从而更好地实现地理空间信息计算。
子午收敛角计算
【实用版】
目录
1.子午收敛角的定义与重要性
2.子午收敛角的计算方法
3.子午收敛角在实际应用中的案例分析
正文
【子午收敛角的定义与重要性】
子午收敛角,又称子午聚散度,是指地球表面上某一点的子午线方向与地球赤道面之间的夹角。
子午收敛角是地球形状和地球表面重力场研究的一个重要参数,它直接影响到地球表面上的测量、定位和地图制图等。
【子午收敛角的计算方法】
子午收敛角的计算公式为:
α = 2 * arcsin[(R * Δlat) / (2 * R * Δlon)]
其中,α表示子午收敛角,R 为地球半径,Δlat 为两点的纬度差,Δlon 为两点的经度差。
根据该公式,可以计算出任意两点之间的子午收敛角。
【子午收敛角在实际应用中的案例分析】
在我国,子午收敛角被广泛应用于大地测量、导航定位、地图制图等领域。
例如,在测量某个地区的经纬度时,需要考虑子午收敛角的影响,以提高测量的精度。
此外,子午收敛角在航空、航天、航海等领域也具有重要意义,因为它直接影响到导航定位的准确性。
总之,子午收敛角是地球形状和地球表面重力场研究的一个重要参数,它在实际应用中具有很高的价值。
第1页共1页。
子午线收敛角的定义
嘿,你知道子午线收敛角是什么吗?简单来说呀,子午线收敛角就是真子午线方向与坐标纵线方向之间的夹角啦!哎呀,就好比你要去一个地方,有一条直直的路(真子午线),还有一条地图上标好的线(坐标纵线),它们之间形成的那个角度就是子午线收敛角哟!比如说你在看地图找路的时候,嘿,这不就跟子午线收敛角有关系嘛!
我是从好多专业的测量学书籍里知道这个的哟!就像那本《测量学基础》,里面详细地介绍了子午线收敛角的各种知识和应用。
这本书啊,就像是一个知识宝库,你打开它,就能发现好多测量学的奥秘呢!它把复杂的概念解释得明明白白,让我们这些普通人也能轻松理解。
怎么样,是不是对子午线收敛角很感兴趣啦?嘿嘿!。
子午线收敛角名词解释子午线收敛角指的是位于垂直平面上与某一子午线平行且方向相反的同一铅垂线上,两条铅垂线所夹的锐角。
它等于90°的余角。
计算公式为: S= 180°-P(式中P为任一无量纲的角)。
因为子午线的半径均相等,所以在任一坐标系统下,子午线的收敛角都相等,并有: S=180°-P 另外我们还可以将∠BCP°=1/2( sinC-sinA)和∠BBP°=1/2( sinB-sinA)合起来求出子午线的收敛角。
角的概念与弧度相似,但不同之处: 1、弧度的概念在弧长单位长度上一段弧所对的圆心角; 2、角的概念指的是平面上一点和任意两条线段或两个平面所成的图形角,如一条直线与经过该点的平面所成的角。
在数学中,一般用符号“∠”表示。
特殊情况下,如果说这个图形是由两条线段围成的,则必须指明是哪两条线段;如果说这个图形是由直线和曲线围成的,则必须指明是直线段还是曲线段。
相关问题1、如何求出地球上某一点的子午线收敛角?利用纬度差和角度,即得所求。
2、求经度差的方法很多,如何求出子午线的收敛角?利用子午线收敛角,即得所求。
3、地球上的两个点A和B如何求出其子午线收敛角?先计算经度差,然后再利用角度。
4、已知A的子午线收敛角B,试求A的经度。
如何利用计算器求出其子午线收敛角?利用弧度的概念,可得A的子午线收敛角,然后根据弧度值查得经度。
5、用天顶角定理求时间轴的正半轴时,如何求出其子午线收敛角?天顶角定理指的是过某一点P(任选)与两条互相垂直的子午线所成的二面角中的任一角都等于90°。
用此定理可求出时间轴的正半轴。
具体做法是:先将时间轴的正半轴标于图中,然后按顺序画出P点与时间轴正半轴的交点P’。
过P’与时间轴正半轴所作的平面截得一矩形,两矩形的交点就是P点,从而确定出P’的位置,使两个平面所截得的矩形的面积相等,也就找到了P点的位置。
若取点P的位置为原点,则过P与原点所作的平面与时间轴的正半轴所作的截得一矩形与过P与原点所作的平面的面积相等,也就确定出P点的位置。
子午线收敛角的计算探讨
令狐文艳
摘要:利用给定的高斯坐标值(x,y)可以通过公式2,3得到其大地经纬度(B,L),得到(B,L)经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。
关键字:子午线坐标正算(反算)大地坐标投影长度比
引言:为了求取子午线收敛角,我们可以有多种方法。
我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{(x,y)—>(B,L)},然后利用L,B就可以求取子午线收敛角。
在测量工作中,经常需要进行正算、反算、换带和子午线收敛角的计算工作。
如图1所示,以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。
显然它与以子午线方向为起始方向的大地方位角A是不相同的,其间的差异即为点P上的大地平行线与子午线之问的夹角y,可称为大地坐标系中点P 上的子午线收敛角,显然就有:γ=A-a+δ
,a=A-γ+δ
式中γ为子午线收敛角,δ为坐标方位角,A为大地方位角,为曲率改正。
正文:
一、通过“1954年北京坐标系”或“1980西安坐标系”的坐
标转化为不同大地坐标L、B。
1. 对于54和80参心坐标系统而言,其坐标系特点比较如下表格。
对于求解大地纬度B,大地经度L需要迭代计算,可以用以下公式直接编写程序求解L、B,理论计算结果2,数值结果2:
(2)
(3)
式中,X为由赤道至纬度B的子午线弧长,为计算点P点与中央子午线的经差。
N为卯酉圈曲率半径,t=tanB,η=e′cosB。
L-L0若以度为单位,则ρ=57.295779513;
L-L0若以分为单位,则ρ=3437.7467708;
L-L0若以秒为单位,则ρ=206264.80625。
上式中,我们利用(x,y)就可以得到(B,L)
二、利用B、L进行高斯投影平面的坐标的计算的变形分析。
首先由于利用高斯投影得到的结果会有投影变形,变形结果如下
1、用大地坐标表示的高斯投影长度比m:
上式中,
用平面坐标表示的高斯投影长度比m
其变形情况如下:
从上式可以发现不同的位置投影长度比m不同,而在同一点处与方向无关。
这符合正形投影特点。
当y=0;
m=1,中央子午线投影长度变形为零。
并随其y的变化而变化。
因而高斯投影得到极大的应用。
三、子午线收敛角的求取
2.、当带入克拉索夫斯基椭球参数进行七次展开,得如下计算公式:
(4)
上式中,t=tanB ,η=e/`cos2B, B为纬度,l经差。
如果将其参数数值带入,可得结果请参见[2]第191页
3、在工程控制测量上我们一般利用如下公式:
(5)
通过参考文献[1]我们发现公式5得到的结果足以达到精度要求。
当得到B、L,就可以并进行公式5就可以得到其子午线收敛角了。
四、结果分析
我们选取东西跨度为41公里、南北跨度21公里范围内均匀分布的38个1980西安坐标系的控制点。
将(x.y)结果带入,利用编写程序进行带入结果可得子午线收敛角有正负之分。
以网格北相对于真北的方向进行判断。
,在中央子午线以东,网格北都在真北以东,可称为东收敛角,收敛角为正值;在中央子午线
以西,网格北都在真北以西,可称为西收敛角,收敛角
为负值。
得到结果;
五、总结
通过结算我们发现可以通过多种方法进行求解子午线收
敛角,利用不同的测量精度要求可以进行不同的处理方
法(改变展开参数次数),可以大大减少处理速度,提
高精度,并可以满足其精度要求。
参考文献:
[1] 邬熙娟,江国焰,高俊强子午线收敛角计算公式及计
算精度分析(南京工业大学土木工程学院。
江苏南京
210009)
[2] 张华海王宝山赵长胜韩晓东等《应用大地测量
学》中国矿业大学出版社
[3] B.H.巴兰金高斯一克吕格投影的子午线收敛角和长度比的计算
[4] 刘福山高斯投影坐标换带和子午线收敛角计算编程长
軎邮电学院面授部长軎 130012
[5] 韩志勇关于子午线收敛角校正问题(中国石油大学(华东)
石油丁程学院,山东东营 257061)。