子午线收敛角计算公式及计算精度分析

工程技术研究2021年第7期242陀螺定向中子午线收敛角的计算方法李泽军中铁一局集团天津建设工程有限公司，天津 300000摘　要：陀螺仪定向是提高隧道定向精度的必要手段，其定向精度不随距离的长短产生误差传递，子午线收敛角γ计算结果的精度直接影响坐标方位角的精度。

文章结合实例计算，表明采用公式γ=sin B ·L 和公式γ=Ky 分别计算得到的子午线收敛角和陀螺推算方位角均可满足工程施工精度要求，因此陀螺定向可为隧道内平面控制网联测和开挖方向的正确性提供检测复核依据，适用于地下工程定向测量。

关键词：子午线收敛角；坐标方位角；陀螺仪中图分类号：P213文献标志码：A文章编号：2096-2789（2021）07-0242-021 子午线收敛角的概念以真子午线为参考，坐标系纵轴X 北端在其东侧时，子午线收敛角为正，反之则为负。

地面上的点纬度B 和中央子午线的距离经差ΔL 决定了子午线收敛角的大小，计算其角值可以用如下近似计算公式：γ=ΔL ·sin B （1）在一个投影带内，高斯平面子午线收敛角的变化遵循一定规律。

距离中央子午线越远，收敛角越大，在中央子午线上收敛角等于零；距离赤道线越远，收敛角越大，在赤道线上收敛角等于零。

2 坐标方位角的换算陀螺仪北方向与真北方向间存在角度偏差，角度的偏差值就是陀螺仪的仪器常数，偏东为正、偏西为负。

坐标北方向与真北方向间的角度偏差就是子午线收敛角，相对真北方向，坐标方位角偏东为正、偏西为负。

陀螺北、真北、坐标北方向关系如图1所示。

陀螺北、真北、坐标北方向之间的角度关系可用如下公式表示：午线与坐标纵线之间的夹角。

坐标纵线东偏为正，西偏为负。

图1陀螺北、真北、坐标北方向关系示意图图2 子午线收敛角概述图赫里斯托夫给出的展至第7次项的计算公式：γ=cos B ×t ×L +cos 3B ×t (1+3η2+2η4)L 3÷3+cos 5B ×t (2t 2+15η2-15η2t 2)L 5÷15+cos 7B ×t (17-26t 2+2t 4)L 7÷315+O(L 7)（3）式中：t =tan B ；η=e′×cos 2B ，e′为第二偏心率；B 为纬度；L 为经差。

子午收敛角计算
【实用版】
目录
1.子午收敛角的定义与重要性
2.子午收敛角的计算方法
3.子午收敛角在实际应用中的案例分析
正文
【子午收敛角的定义与重要性】
子午收敛角，又称子午聚散度，是指地球表面上某一点的子午线方向与地球赤道面之间的夹角。

子午收敛角是地球形状和地球表面重力场研究的一个重要参数，它直接影响到地球表面上的测量、定位和地图制图等。

【子午收敛角的计算方法】
子午收敛角的计算公式为：
α = 2 * arcsin[(R * Δlat) / (2 * R * Δlon)]
其中，α表示子午收敛角，R 为地球半径，Δlat 为两点的纬度差，Δlon 为两点的经度差。

根据该公式，可以计算出任意两点之间的子午收敛角。

【子午收敛角在实际应用中的案例分析】
在我国，子午收敛角被广泛应用于大地测量、导航定位、地图制图等领域。

例如，在测量某个地区的经纬度时，需要考虑子午收敛角的影响，以提高测量的精度。

此外，子午收敛角在航空、航天、航海等领域也具有重要意义，因为它直接影响到导航定位的准确性。

总之，子午收敛角是地球形状和地球表面重力场研究的一个重要参数，它在实际应用中具有很高的价值。

第1页共1页。

子午线收敛角的计算子午线收敛角的计算探讨摘要：利用给定的高斯坐标值（x,y）可以通过公式2,3得到其大地经纬度（B,L），得到（B,L）经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。

关键字：子午线坐标正算（反算）大地坐标投影长度比引言：为了求取子午线收敛角，我们可以有多种方法。

我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{（x，y）—>（B，L）}，然后利用L，B就可以求取子午线收敛角。

在测量工作中，经常需要进行正算、反算、换带和子午线收敛角的计算工作。

如图1所示，以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。

显然它与以子午线方向为起始方向的大地方位角A是不相同的，其间的差异即为点P上的大地平行线与子午线之问的夹角y，可称为大地坐标系中点P上的子午线收敛角，显然就有：γ=A-ａ+δ，ａ=A-γ+δ式中γ为子午线收敛角，δ为坐标方位角，A为大地方位角，为曲率改正。

正文：一、通过“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不同大地坐标L、B。

1. 对于54和80参心坐标系统而言，其坐标系特点比较如下表格。

对于求解大地纬度B，大地经度L需要迭代计算，可以用以下公式直接编写程序求解L、B,理论计算结果2，数值结果2： (2) (3)式中，X为由赤道至纬度B的子午线弧长，为计算点P点与中央子午线的经差。

N为卯酉圈曲率半径，t=tanB，η=e′cosB。

L-L0若以度为单位，则ρ=57.295779513；L-L0若以分为单位，则ρ=3437.7467708;L-L0若以秒为单位，则ρ=206264.80625。

上式中，我们利用（x,y）就可以得到（B,L）54年北京坐标系克拉索夫斯基椭球；参心坐标系长半轴a=6378245m；短半轴扁率α=1：298.3。

大地原点在原苏联的普尔科沃采用多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳；参心坐标系长半轴a=637814m；短半轴b=6356755.29m；扁率α=1：298.257；大地原点在陕西省泾阳县永乐镇；椭球短轴平行于地球地轴起始子午面平行于格林威治天文台平均子午面二、利用B、L进行高斯投影平面的坐标的计算的变形分析。

子午线收敛角计算公式及计算精度分析以《子午线收敛角计算公式及计算精度分析》为标题，本文将对子午线收敛角的定义、物理意义和计算公式进行详细分析，并对子午线收敛角计算的精度做出评估。

子午线收敛角是一种定义在空间曲率理论上的角度，它描述在一个曲率空间中两个不同子午线之间角度的变化情况。

它被用来描述万有引力场的形状，如地球表面的地貌等。

子午线收敛角是非常重要的度量，具有重要的物理意义。

子午线收敛角的计算公式可以从拉格朗日系数表示法中推出：$$ phi= frac{1}{2} sum_{i=1}^{3} (gamma_{ii} - gamma_{jj}) cdot Delta theta_{ij} $$其中，$gamma_{ij}$表示拉格朗日系数; $Delta theta_{ij}$表示两个子午线之间的夹角。

这里要计算子午线收敛角可以使用上述公式。

此公式计算结果对于子午线收敛角的精度有一定要求，如果计算结果误差大，会对实际应用造成影响。

为了评估子午线收敛角的计算精度，一种常用的方法是使用仿真数据。

在仿真实验中，通过改变空间曲率参数，产生不同子午线收敛角的情况，从而获得理想的测量结果。

用这些理想结果与计算结果比较，就可以评估子午线收敛角计算的精度了。

此外，为了提高子午线收敛角计算精度，还可以使用多种数值计算方法，比如拉格朗日元法、二阶中心差分法等。

这些方法都可以得到更精确的子午线收敛角计算结果，可以提供更准确的计算结果以满足应用需求。

综上所述，子午线收敛角是一种定义在空间曲率理论上的角度，可以用来描述万有引力场的形状，具有重要的物理意义。

计算子午线收敛角可以使用拉格朗日系数表示法中推导出的公式。

为了评估子午线收敛角计算的精度，可以使用仿真数据，也可以使用多种数值计算方法来提高计算精度。

本文根据子午线收敛角的定义、物理意义和计算公式，以及计算精度，对子午线收敛角做出了全面分析。

子午线收敛角计算公式及计算精度分析子午线收敛角，也叫做子午线弯曲角，是衡量地球的一种重要的球面度量。

当地球的子午线既不是完全水平也不是完全垂直的时候，它就会产生弯曲，这种弯曲就叫做子午线收敛角。

子午线收敛角的弯曲大小决定了地球的子午线的收缩和延伸，从而决定地球的经纬度系统及坐标坐标形式。

子午线收敛角的计算方法有多种，其中最常用的就是基于子午线收敛角的计算公式。

1.子午线收敛角的计算公式基于子午线收敛角的计算公式有两种，第一种是WaIters公式（WaIters formula），它的公式为：$$Δ= arccos(frac {s_1-s_2}{s_1+s_2} )$$其中，Δ是子午线收敛角，s1、s2分别是子午线两点的大圆距离。

WaIters公式利用大圆距离来计算子午线收敛角，它可以用来计算椭圆面子午线收敛角，但是它计算精度受到大圆距离精度的限制，其精度为1分。

第二种是瓦特斯-贝塞尔公式（Waters-Bessel formula），它的公式为：$$Δ＝arccos(frac {s_1^2-s_2^2}{s_1^2+s_2^2})$$ 其中，Δ是子午线收敛角，s1、s2分别是子午线两点的球面坐标的经纬差。

瓦特斯-贝塞尔公式利用球面坐标经纬差计算子午线收敛角，是WaIters公式的一种改进，它可以用来计算椭圆及偏心率修正后的球体子午线收敛角，其精度可以达到1厘米。

2.子午线收敛角计算精度分析子午线收敛角的计算精度受多种因素的影响，其中最主要的是地球的椭球体模型精度和地理坐标测量精度。

（1）影响地球椭球体模型精度的因素地球椭球体模型的精度受到各种因素的影响，例如，地球的大小、形状、弹性模量、重力系数、质量、质心定位等。

由于这些因素都是比较复杂的物理模型，因此，地球椭球体模型精度受到较大的影响，其精度通常在3到5厘米之间。

（2）影响地理坐标测量精度的因素地理坐标测量精度受多种因素的影响，如地理坐标测量仪器、标定结果、大圆距离测量精度等。

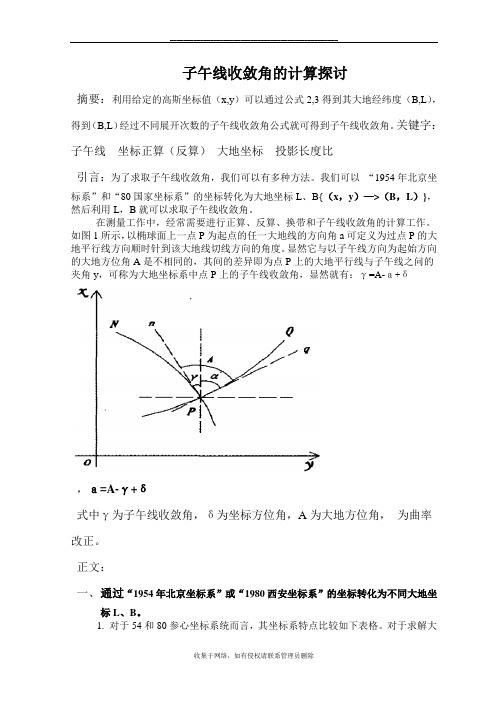
子午线收敛角的计算探讨摘要：利用给定的高斯坐标值（x,y）可以通过公式2,3得到其大地经纬度（B,L），得到（B,L）经过不同展开次数的子午线收敛角公式就可得到子午线收敛角。

关键字：子午线坐标正算（反算）大地坐标投影长度比引言：为了求取子午线收敛角，我们可以有多种方法。

我们可以“1954年北京坐标系”和“80国家坐标系”的坐标转化为大地坐标L、B{（x，y）—>（B，L）}，然后利用L，B就可以求取子午线收敛角。

在测量工作中，经常需要进行正算、反算、换带和子午线收敛角的计算工作。

如图1所示，以椭球面上一点P为起点的任一大地线的方向角a可定义为过点P的大地平行线方向顺时针到该大地线切线方向的角度。

显然它与以子午线方向为起始方向的大地方位角A是不相同的，其间的差异即为点P上的大地平行线与子午线之问的夹角y，可称为大地坐标系中点P上的子午线收敛角，显然就有：γ=A-ａ+δ，ａ=A-γ+δ式中γ为子午线收敛角，δ为坐标方位角，A为大地方位角，为曲率改正。

正文：一、通过“1954年北京坐标系”或“1980西安坐标系”的坐标转化为不同大地坐标L、B。

1. 对于54和80参心坐标系统而言，其坐标系特点比较如下表格。

对于求解大地纬度B，大地经度L需要迭代计算，可以用以下公式直接编写程序求解L、B,理论计算结果2，数值结果2： (2) (3)式中，X为由赤道至纬度B的子午线弧长，为计算点P点与中央子午线的经差。

N为卯酉圈曲率半径，t=tanB，η=e′cosB。

L-L0若以度为单位，则ρ=57.295779513；L-L0若以分为单位，则ρ=3437.7467708;L-L0若以秒为单位，则ρ=206264.80625。

上式中，我们利用（x,y）就可以得到（B,L）54年北京坐标系克拉索夫斯基椭球；参心坐标系长半轴a=6378245m；短半轴扁率α=1：298.3。

大地原点在原苏联的普尔科沃采用多点定位法进行椭球定位80年西安坐标系椭球面与似大地水准面密合得最佳；参心坐标系长半轴a=637814m；短半轴b=6356755.29m；扁率α=1：298.257；大地原点在陕西省泾阳县永乐镇；椭球短轴平行于地球地轴起始子午面平行于格林威治天文台平均子午面二、利用B、L进行高斯投影平面的坐标的计算的变形分析。

子午线收敛角计算公式及计算精度分析子午线收敛角是测量我们在地球上的位置的方法之一。

然而，它的计算精度至关重要，因为它是一种3D投影的基础。

因此，本文的主要目的是探讨子午线收敛角的计算公式和精度，以及如何减少计算的错误。

一、子午线收敛角的定义子午线收敛角是地图学上的一项基本概念，它指的是把地球上的一点线性投射到地图上时，投射端点与子午线之间的夹角。

子午线是地球上经度方向上的一条线，与地球赤道平行，地球上每一点的子午线都不同。

子午线收敛角用θ(θ <90°)表示，其计算公式为：θ=arccos（cosφ1cosφ2sin（λ2-λ1）+sinφ1sinφ2）其中，λ和φ是投影点的经度和纬度。

二、子午线收敛角的计算精度计算子午线收敛角的精度主要取决于地球模型的精度，它是空间位置信息计算的基础。

如果地球模型精度低，会影响子午线收敛角计算的精度，甚至产生误差。

例如，在地球表面变形较重的地区，如山区，可能会产生较大的误差。

实际计算过程中，计算机还会对数字的计算和精度有一定的影响。

例如，在电脑上使用浮点精度（float），这种计算精度远远不及双精度（double），因此会出现精度丢失的情况。

三、如何减少计算误差以上是子午线收敛角的计算公式和精度分析，下面我们来讨论如何减少计算误差。

首先，对地球模型进行精确测量，以减少误差。

其次，有必要采用更高精度的计算方式，例如双精度计算法，减少计算误差。

再者，可以使用更精确的坐标系统，例如WGS84，准确计算子午线收敛角。

此外，在计算过程中使用合适的中间计算空间，例如椭球面，有助于计算子午线收敛角的精度。

本文简要介绍了子午线收敛角的计算公式及其计算精度分析，以及如何减少计算误差的方法。

通过有效的采用更精准的计算方法，选择更好的投影体系，以及使用适合的计算空间，可以有效提高子午线收敛角的计算精度，从而更好地实现地理空间信息计算。

子午收敛角计算
摘要：
一、子午收敛角定义
二、子午收敛角计算方法
1.坐标系选择
2.计算公式
三、子午收敛角的应用
1.天文学领域
2.导航定位技术
3.地球物理学
正文：
子午收敛角是地球表面上某一点与本初子午线的夹角，用以描述地球表面上某一点的经度。

对于科学研究和实际应用而言，精确计算子午收敛角具有重要意义。

首先，要计算子午收敛角，需要选择合适的坐标系。

通常情况下，可以选择地理坐标系、地心坐标系或者地球参考系统。

这些坐标系的选择会影响到子午收敛角的计算结果。

其次，根据所选坐标系，可以采用不同的计算公式来求解子午收敛角。

一般来说，计算公式包括地球椭球参数、地球自转角速度、观测高度等因素。

通过将这些因素代入公式，可以得到子午收敛角的数值。

在实际应用中，子午收敛角广泛应用于天文学领域。

在天文学研究中，精
确测量天体的位置和运动轨迹是至关重要的。

子午收敛角作为地球表面上某一点的经度表示，对于分析天体的运动规律具有关键作用。

此外，在导航定位技术中，子午收敛角也是不可或缺的参数。

卫星导航系统需要精确测量地球表面上某一点的经度，以便为用户提供准确的导航信息。

通过计算子午收敛角，可以提高导航定位的精度和可靠性。

在地球物理学领域，子午收敛角同样具有重要意义。

地球物理学家利用子午收敛角来研究地球内部的构造和物理性质，为地震预测、地壳稳定性分析等提供重要依据。

总之，子午收敛角计算在科学研究和实际应用中具有广泛应用。

子午收敛角计算
摘要：
1.子午收敛角的定义与重要性
2.子午收敛角的计算方法
3.子午收敛角的应用实例
正文：
一、子午收敛角的定义与重要性
子午收敛角，又称子午聚光角，是指在光学系统中，光线通过透镜或反射镜等光学元件后，汇聚于一点形成的角度。

子午收敛角是衡量光学系统成像质量的重要参数，对于光学仪器的设计、制造和使用具有重要的实际意义。

二、子午收敛角的计算方法
子午收敛角的计算方法有多种，其中较为常见的有以下两种：
1.薄透镜公式法
薄透镜公式是计算子午收敛角的一种简便方法。

对于一个薄凸透镜，其子午收敛角可用以下公式计算：
α= (n - 1) * θ
其中，α表示子午收敛角，n 表示透镜材料的折射率，θ表示入射光线与光轴的夹角。

2.光学投影法
光学投影法是利用光学投影原理，通过绘制光学系统的光路图，进而计算子午收敛角。

此方法适用于复杂光学系统，但计算过程较为繁琐。

三、子午收敛角的应用实例
子午收敛角在光学领域的应用广泛，以下以照相机镜头的设计为例，介绍子午收敛角的应用：
在照相机镜头设计中，为了保证成像质量，需要使光线在经过镜头后能够汇聚于一点，形成清晰的像。

这就要求设计者要充分考虑子午收敛角的大小，以及不同光圈下子午收敛角的变化。

通常，镜头的子午收敛角会随着焦距的增加而减小，这意味着长焦镜头的成像质量往往优于短焦镜头。