水文频率分析方法
- 格式:doc
- 大小:1.63 MB
- 文档页数:10

水文频率分析范文水文频率分析是指对水文数据进行统计与分析,以获取水文过程的频率特征。
频率特征是水文研究和水资源管理的重要内容,对于水文过程的认识和预测具有重要意义。
下面将从频率分析的目的、方法和应用等方面进行详细阐述。
一、频率分析的目的1.揭示水文要素的概率分布:通过对水文观测数据进行频率分析,可以得到水文要素(如降雨量、径流量等)的概率分布特征,包括表达其中心位置、离散程度和形状等参数。
2.评估极端事件的可能性:频率分析可以用于评估极端水文事件(如洪水、旱情等)发生的概率,进而为水资源规划和防灾减灾提供科学依据。
3.提供设计水文统计指标:频率分析可根据工程需求,提供一系列设计水文统计指标,如设防洪水位、取水量的最低保证率等,为水利工程规划和设计提供理论依据。
二、频率分析的方法1.构建概率分布函数:常用的概率分布函数有正态分布、对数正态分布、伽玛分布等,将观测数据拟合到适当的概率分布函数中,以反映其频率特征。
2.估计参数:对于选定的概率分布函数,需要通过参数估计的方法来确定其参数值,常用的估计方法有矩估计法、极大似然估计法、贝叶斯估计法等。
3. 拟合度检验:利用拟合度检验检验选定的概率分布函数与观测数据的拟合程度,常用的检验方法有卡方检验、Kolmogorov-Smirnov检验等。
4.经验公式法:经验公式法是根据大量的实测资料,通过统计方法建立的经验公式,常用于快速估计设计水文统计指标,如暴雨量、设计洪水等。
三、频率分析的应用1.洪水预报与防洪调度:通过对历史洪水资料的频率分析,可以估计其中一水位、流量或洪峰值发生的概率,进而进行洪水预警和防洪调度。
2.水资源管理与规划:频率分析可以为水资源管理提供重要的科学依据,包括合理配置水资源、制定水资源管理方案、制定取水许可计划等。
3.城市排水系统设计与规划:频率分析可用于城市排水系统的设计与规划,包括雨洪分析,计算合理设防洪水位,为城市排水系统的设计提供参考。


水文频率分析水文频率分析hydrologic frequency analysis根据某水文现象的统计特性,利用现有水文资料,分析水文变量设计值与出现频率(或重现期)之间的定量关系。
自然界的现象按发生情况可分成:必然事件,即在一定条件下必然会发生的事情,如降雨以后就要涨水是必然发生的;不可能事件,即在各条件实现之下永远不会发生的事情,如只在重力作用下的水由低处向高处流是不可能的;随机事件(也称偶然事件),即在一定条件下可能发生也可能不发生的事件,如每条河流每年出现一个流量的年最大值是必然的,但这个最大值可能是这个值也可能是那个值,它在数量上的出现是一种随机事件。
频率计算中是以1来表示必然事件出现的可能性(即百分之百出现),以0表示不可能事件出现的可能性,随机事件出现的可能性介于0与1之间。
水文要素如降雨、流量等在量的出现方面都有随机性的特点,水文变量如年雨量、年最大洪峰流量、枯季最小流量等都属于随机事件,均可用频率分析方法来分析计算。
水文频率分析主要包括:利用现有水文资料组成样本系列,选择合适的频率曲线线型和估计它的统计参数,根据所绘制的频率曲线推求相应于各种频率(或重现期)的水文设计值。
样本系列无限个成因相同、相互独立的同类水文变量的集合称为该水文变量的总体。
这个总体是未知的,现有水文资料只是过去发生过的和今后可能发生的整个总体中的一个样本。
把现有水文资料的水文变量按大小次序排列组成一个系列,称为样本系列,其中所含水文变量的项数(系列长度)叫做样本容量。
系列愈长,样本容量愈大。
水文频率分析就是通过样本系列的统计特征来估计其总体的统计特征,如各种统计参数、某水文变量的频率等。
因此,样本系列是水文频率分析的基础。
用样本系列去推估容量很大或无限的总体的情况,会产生因抽样而引起的误差,这就是抽样误差。
水文统计分析中所估计出的各种数值(如频率、分析中的各个参数、相关系数等)都有抽样误差。
样本的容量越大误差越小,否则误差越大。

计算说明书━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━工程名称:工程1计算类型:水文频率分析计算(P-Ⅲ型曲线)一、计算原理1.适用范围本程序可一次完成一个水文系列频率计算的全部工作,对连续系列和不连续系列均为适用。
本程序完成的工作内容包括:系列排队、计算经验频率及统计参数值、通过优选P-Ⅲ型曲线的参数Cv、Cs值进行适线或用目估法适线、绘制频率曲线图、计算所采用的频率曲线的各设计频率下的设计值等。
为满足工程的实际需要,本程序除可用优选统计参数的方法适线外,还可用目估适线法进行适线。
因为本程序在用优选法适线时,对各经验点据是给以等权重的处理。
而当需要对各点据给以非等权重的处理时(如:设计洪水中要求多照顾首几项洪水;在年径流计算时要多照顾末端;或由于基本资料精度差等),单用优选法就不合适,此时可改用目估适线法。
为了减少目估适线时的盲目性,实际使用时,一般采用优选与目估适线相结合的方法,即先用优选法选出一条通过点群中心的频率曲线。
在此基础上再用目估的方法对优选出的参数Cv、Cs做少许调整,重新适线,以达到对各点据给以不同权重的目的,获得满意的结果。
2.计算方法和公式3.规范规程(1)《水利水电工程设计洪水计算规范》(SL44-2006)(2)《水利水电工程水文计算规范》(SL278-2002)4.参考文献(1)《水利水电工程设计洪水计算手册》水利部长江水利委员会水文局水利部南京水文水资源研究所主编,1995年10月(2)《工程水文学》(第三版)武汉大学叶守泽,河海大学詹道江合编,中国水利水电出版社,2000年10月(3)《最优化理论与算法》(第二版)陈宝林编著,清华大学出版社,2005年10月(4)《水利水电工程设计计算程序集 A-3 水文频率计算程序》作者马明(新疆水利水电勘测设计院)(5)《Visual Basic常用数值算法集》何光渝编著,科学出版社,2002年(6)《科学与工程数值算法〔Visual Basic版〕》周长发编著,清华大学出版社,2002年二、基本数据连续系列项数n=33序位系列值编号1 1952 114.002 1953 118.003 1954 116.004 1955 105.005 1956 122.006 1957 88.807 1958 141.008 1959 132.009 1960 107.0010 1961 94.8011 1962 94.0012 1963 113.0013 1964 114.0014 1965 101.0015 1966 104.0016 1967 92.8017 1968 97.1018 1969 116.0019 1970 122.0020 1971 145.0021 1972 119.0022 1973 111.0023 1974 83.1024 1975 93.5025 1976 104.0026 1977 88.5027 1978 95.3028 1979 92.5029 1980 115.0030 1981 94.5031 1982 107.0032 1983 90.9033 1984 89.10三、计算结果1.统计参数值:均值 Xa=106.694均方差 S=15.308变差系数Cv=0.143偏态系数Cs=0.708Cs/Cv=4.934经验频率值表序位系列值频率(%)编号1 1971 145.000 2.9412 1958 141.000 5.8823 1959 132.000 8.8244 1970 122.000 11.7655 1956 122.000 14.7066 1972 119.000 17.6477 1953 118.000 20.5888 1969 116.000 23.5299 1954 116.000 26.47110 1980 115.000 29.41211 1964 114.000 32.35312 1952 114.000 35.29413 1963 113.000 38.23514 1973 111.000 41.17615 1960 107.000 44.11816 1982 107.000 47.05917 1955 105.000 50.00018 1966 104.000 52.94119 1976 104.000 55.88220 1965 101.000 58.82421 1968 97.100 61.76522 1978 95.300 64.70623 1961 94.800 67.64724 1981 94.500 70.58825 1962 94.000 73.52926 1975 93.500 76.47127 1967 92.800 79.41228 1979 92.500 82.35329 1983 90.900 85.29430 1984 89.100 88.23531 1957 88.800 91.17632 1977 88.500 94.11833 1974 83.100 97.0592.优选P-Ⅲ型曲线的参数Cv、Cs值(离差平方和准则):离差平方和S=148.063Xa=107.218Cv=0.157Cs=1.053Cs/Cv=6.7113.理论频率曲线设计值(目估适线):Xa=107.218Cv=0.157Cs=1.053Cs/Cv=6.711理论频率曲线设计值表频率P(%) 模比系数Kp 设计值Xp B 绝对误差δXp 相对误差δ'Xp(%)0.01 1.954 209.467 11.46 33.551 16.017 0.1 1.723 184.710 8.09 23.694 12.828 0.2 1.651 177.039 7.06 20.665 11.6730.5 1.555 166.681 5.71 16.734 10.0401 1.480 158.636 4.72 13.822 8.7132 1.402 150.357 3.77 11.053 7.3513 1.356 145.388 3.13 9.166 6.3045 1.296 138.942 2.74 8.038 5.78510 1.210 129.76620 1.118 119.84630 1.058 113.48140 1.012 108.54250 0.973 104.32160 0.937 100.48370 0.903 96.77280 0.867 92.92090 0.825 88.42995 0.796 85.39297 0.781 83.71999 0.757 81.12299.9 0.728 78.104四、图形结果────────────────────────────────────────────────────────计算软件:SGGH-Tools 2011 计算者:校核者:计算日期:2020/8/24。

如何进行水文测量与数据分析水文测量与数据分析是水资源管理和环境保护的重要组成部分。
它们可以帮助我们了解水文过程,预测洪水和干旱,以及为水资源规划提供数据支持。
在本文中,我们将探讨如何进行水文测量与数据分析的方法和技巧。
一、水文测量的方法水文测量是指测量和记录水文要素的过程,如河流流量、降雨量和蒸发量。
以下是几种常用的水文测量方法:1. 流量测量:测量河流或水道中水流通过的量。
最常见的方法是使用流速仪和测流船,将流速和横截面积结合起来计算流量。
2. 降雨量测量:测量降水的数量和强度。
常用的方法包括雨量计和雷达测量。
雨量计是一种简单的装置,用于测量降水量,而雷达测量可以提供更广泛的资料。
3. 蒸发量测量:测量水体表面上蒸发的水量。
常用的方法包括蒸发皿法和蒸发计法。
蒸发皿法是将水放置在平底容器中,通过测量水位下降来计算蒸发量。
蒸发计法是使用蒸发计仪器测量空气中的蒸发。
二、数据分析方法完成水文测量后,我们需要对数据进行分析和解释。
以下是几种常用的数据分析方法:1. 趋势分析:通过分析长期的数据序列,确定水文要素的变化趋势。
常用的方法包括线性回归和滑动平均法。
线性回归可以确定变量之间的线性关系,并预测未来的变化。
滑动平均法可以平滑数据序列,以识别潜在的趋势。
2. 频率分析:通过计算不同频率的事件发生概率来评估极端水文事件的可能性。
常用的方法包括频率分布函数和极值分布函数。
频率分布函数可以根据观测值的频率来估计概率。
极值分布函数可以估计罕见事件的概率。
3. 空间分析:通过分析不同地点的水文要素数据,了解不同地区的水文特征。
常用的方法包括地理信息系统(GIS)和空间插值法。
GIS可以将不同地点的数据集成在一起,并提供地图和空间分析工具。
空间插值法可以通过已知的测量点估算未知点的数值,以生成连续的空间分布。
三、数据质量控制在进行水文测量和数据分析时,数据质量控制非常重要。
以下是几种常用的数据质量控制方法:1. 数据验证:将测量数据与其他可靠数据进行比对,以确保其准确性和一致性。

第五章水文统计的基本知识及方法研究内容:主要有频率计算与相关分析。
频率计算,包括随机变量及其概率分布、水文频率曲线、适线法等;相关分析,包括简相关与复相关。
研究目的:研究河川径流的统计规律,预估径流的变化趋势,以满足水利水电工程规划、设计、施工和运行管理的需要。
第一节概述概率论与数理统计是一门研究客观事物偶然性(随机性)规律的学科。
由于水文现象一般都具有偶然性的特点,所以,可以用数理统计的原理和方法分析研究它的变化规律。
这种方法称为水文统计法。
工程水文计算中运用水文统计法,不仅合理,而且是必要的。
例如,流域开发,首先要搞清未来河流水量的多少;设计拦河坝、堤防工程需要知道未来时期当地洪水的大小。
这些都要求对未来长期的径流形势做出估计。
如果所建工程计划使用100年,那么就要对未来100年的径流形势做出估计。
但是,由于影响径流的因素众多,难以基于必然现象的规律,应用成因分析法对径流做出这样长期的时序定量预报,而只能基于统计规律,运用数理统计方法对径流做出概率预估,以满足工程设计的需要。
第二节概率的基本概念一、试验和事件在概率论中, 对随机现象的测验叫做随机试验,随机试验的特点是限定条件,重复做。
随机试验的结果称为事件。
根据事件发生的可能性,事件可以分为三类:1、必然事件:在一定试验条件下,试验结果中必然会发生的事件;2、不可能事件:在一定试验条件下,试验结果中决不会发生的事件;3、随机事件:在一定试验条件下,试验结果中可能发生也可能不发生的事件。
二、概率随机事件出现的可能性或机率叫概率。
随机事件A发生的概率用P(A)表示,以百分数计。
显然,必然事件概率为1;不可能事件的概率为0;随机事件的概率介于0和1之间。
如果某试验可能发生的结果总数是有限的,并且所有结果出现的可能性是相等的,称之为古典概型事件。
在古典概型事件中,如果可能发生的结果总数为n,而事件A有其中的m个结果,则随机事件A发生的概率P(A)为:P(A)=m/n 5-1水文事件一般不能归为古典概型事件。


工程水文学同频率法计算工程水文学中的同频率法计算主要包括以下七个方面:1.洪水频率分析洪水频率分析是工程水文学中重要的一部分,主要用于研究洪水的频率和特征。
进行洪水频率分析时,首先需要收集历年的洪水数据,包括洪水的过程线、峰值流量、洪水总量等,然后根据这些数据确定洪水频率曲线。
洪水频率分析的主要步骤包括:数据收集、洪水过程线构建、洪水频率曲线拟合、洪水图表绘制等。
2.暴雨频率分析暴雨频率分析主要是用来研究暴雨的频率和特征。
进行暴雨频率分析时,需要收集历年的暴雨数据,包括暴雨的过程线、降雨量、降雨时间等,然后根据这些数据确定暴雨频率曲线。
暴雨频率分析的主要步骤包括:数据收集、暴雨过程线构建、暴雨频率曲线拟合、暴雨图表绘制等。
3.河流流量变化分析河流流量变化分析主要是用来研究河流流量的变化特征。
进行河流流量变化分析时,需要收集历年的河流流量数据,包括洪水期和非洪水期的流量值,然后根据这些数据确定河流流量变化曲线。
河流流量变化分析的主要步骤包括:数据收集、河流过程线构建、河流流量变化曲线拟合、河流图表绘制等。
4.水库调度模拟水库调度模拟主要是用来研究水库的调度过程和效果。
进行水库调度模拟时,需要收集历年的水库调度数据,包括入库流量、出库流量、水位等,然后根据这些数据模拟水库的调度过程。
水库调度模拟的主要步骤包括:数据收集、水库调度线构建、水库调度模型拟合、水库调度图表绘制等。
5.水位流量关系推求水位流量关系推求主要是用来研究水位和流量之间的关系。
进行水位流量关系推求时,需要收集历年的水位和流量数据,然后根据这些数据确定水位流量关系曲线。
水位流量关系推求的主要步骤包括:数据收集、水位流量关系构建、参数拟合、水位流量图表绘制等。
6.输水渠道水位流量推求输水渠道水位流量推求主要是用来研究输水渠道的水位和流量之间的关系。
进行输水渠道水位流量推求时,需要收集输水渠道的水位和流量数据,然后根据这些数据确定输水渠道水位流量关系曲线。

可见,灌区内浅层地下水主要消耗于人工开采消耗,占总消耗量的55%以上。
3.4.3浅层地下水量计算在合理埋深的条件下,计算灌区浅层含水层的储存量,其计算结果为Q储存=0.9亿m3/a。
由此可见,灌区浅层地下水具有巨大的储存能力,同时具有良好的调节能力。
3.5结果分析3.5.1地下水位变化分析从位于灌区内邓李乡湾刘村6号观测井和龚店乡台马村13号观测井地下水位埋深多年变化图来看,灌区内地下水位变化很小,埋深都是在2.0~4.0m之间变动。
3.5.2结论一是白龟山灌溉补源占到灌区内浅层地下水补源总量的37%,加上水库侧渗补源,白龟山水库对灌区地下水的补源占总补源量的51%,对涵养区域地下水资源发挥了主导作用;二是灌区内地下水位长期稳定,埋深浅,与相近的甘江河南岸相比,地下水埋深高出8 ̄10m,为今后地下水开发利用提供了较好的前提条件;三是根据分析计算,区域内浅层地下水总量为0.9亿m3/a,可采资源量为0.590亿m3/a。
收稿日期:2012-01-061.问题的提出1975年8月,河南省中南部的沙颍河、洪汝河等水系发生了特大暴雨,出现了建国以来罕见的特大洪水,导致了境内的板桥和石漫滩两座大型水库垮坝,给全省乃至全国水利界带来很大的震动和反思。
这次史称“75·8”的特大暴雨洪水,刷新了许多水文要素国内实测系统值的记录。
洪水过后,河南水利界的反思之一就是对境内所有大型水库的规划指标进行了重新修订。
笔者通过比较发现,在规划频率不变的情况下,一些水库(如:板桥、薄山、陆浑等)的规划值修订前后发生了很大变化,这实际上是由于规划时进行水文频率计算的误差造成的。
水文频率计算的误差在教科书和水文规范中虽然没有提及,但在实际工作中却经常遇到。
2.频率计算概述水文频率计算是水文资料应用于国民经济其它行业规划时的最常用计算之一。
常用的经验频率公式为Pm=mn+1(其中n为资料系列长度,m为所选水文要素排序后的序号)。
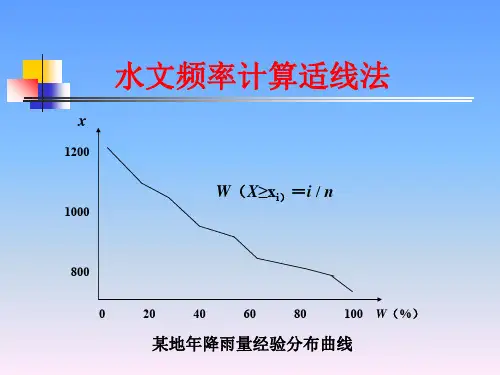

权函数水文频率分析方法的一种应用权函数水文频率分析方法是一种常用的水文学分析方法,用于研究水文过程中的概率分布和频率分析。
在水文学中,频率分析是评估罕见事件发生概率的重要方法,例如洪水、干旱等。
本文将介绍权函数水文频率分析方法的一种应用,即用于洪水频率分析。
洪水频率分析是水文学中非常重要的内容之一,它用于确定一定概率下的洪水流量。
基于洪水过程的特点,可以使用一系列维度进行洪水频率分析,例如洪水的最大值、洪峰流量等。
权函数水文频率分析方法是一种基于概率论和数理统计的方法,通过建立洪水概率分布函数,推测不同概率水平下的洪水流量。
权函数水文频率分析方法的核心思想是建立洪水的频率-概率关系,即通过历史洪水资料的统计分析,建立洪水流量和概率的数学函数关系。
在权函数水文频率分析方法中,首先需要建立频率分布函数,并且选择合适的数学函数形式来描述洪水频率-概率关系。
常用的函数形式包括正态分布函数、指数分布函数、威布尔分布函数等。
在应用权函数水文频率分析方法时,需要进行以下步骤:1.数据收集:收集具有连续观测记录的洪水数据,包括洪水流量、降雨量等。
数据的质量和连续性对于频率分析结果至关重要。
2.初步处理:对收集到的洪水数据进行初步处理,包括数据的检验、填补缺失值等。
确保数据的完整性和准确性。
3.频率分布函数的选择:根据洪水观测数据的性质,选择合适的频率分布函数来描述洪水频率分布。
常用的函数形式包括正态分布、对数正态分布、威布尔分布等。
4.参数估计:使用最大似然估计方法或其他参数估计方法,确定频率分布函数的参数。
该步骤可以通过统计软件来实现。
5.频率分析和设计值确定:根据确定的频率分布函数和参数,计算不同概率下的洪水流量或洪峰流量。
常用的频率包括设计洪水的不同概率,如10年一遇洪水、50年一遇洪水等。
6.结果应用:根据计算得到的洪水流量或洪峰流量,进行工程设计、风险评估等应用。
例如,可以用于城市排水系统设计、堤防设计等。
掌握水文测量与水文数据分析方法导言水文测量与水文数据分析是水文学领域中不可或缺的重要研究方法。
通过对水文数据的收集、处理和分析,我们可以深入了解水文过程及其变化规律,为水资源管理、防洪减灾等方面提供科学依据。
本文将介绍水文测量的基本原理和方法,以及水文数据分析的常用技巧和应用。
一、水文测量基本原理与方法水文测量是指对水文要素进行定量测量,包括水位、流量、降雨等指标的观测。
水文测量的基本原理是根据物理量与测量量之间的关系建立测量模型,并利用测量仪器设备进行实验获取数据。
以下将介绍水位测量和流量测量两个方面的基本原理和方法。
1. 水位测量原理与方法水位是指水面到某一基准面的垂直距离,常用的水位测量方法包括测水尺法、气压计法和流速计法等。
测水尺法是指利用测水尺或水位计测量水位的方法,适用于静态水体的测量。
气压计法是根据大气压力与水面高度之间的关系进行测量,通过气压计可以间接计算出水位高度。
流速计法是指通过测量水流速度来推断水位的高低,根据流速与水位之间的函数关系得出结果。
2. 流量测量原理与方法流量是单位时间内通过给定断面的水量,常用的流量测量方法包括浮物法、比弗法和多点测流法等。
浮物法是指在水流中放入已知浮标,通过跟踪浮标的运动轨迹来计算流速和流量。
比弗法是通过岸边测量断面宽度和水深,计算出流速和流量。
多点测流法是在断面上设立多个测点,测量不同点位的流速,从而推算出流量。
二、水文数据分析的常用技巧和应用水文数据分析是对收集到的水文数据进行处理和分析的过程,可以揭示水文过程的规律和特点,为相关研究和工作提供依据。
下面将介绍一些常用的水文数据分析技巧和应用。
1. 描述性统计分析描述性统计分析是对水文数据的基本特征进行统计和描述,主要包括均值、方差、分布形状等方面的指标。
通过对水文数据的描述性统计分析,我们可以了解数据的集中趋势和离散程度,为后续分析和应用提供参考。
2. 趋势分析趋势分析是指对水文数据的变化趋势进行研究和分析,可以揭示水文过程的长期变化规律。
新安水文站长历时暴雨量频率分析随着全球气候变化的加剧,暴雨天气频繁发生,造成了一系列的灾害和损失。
为了做好防洪减灾工作,需要对历时暴雨量频率进行分析和研究。
本文将对新安水文站长历时暴雨量频率进行详细分析,并提出相应的防洪减灾建议。
1. 研究背景新安水文站位于某省某市,是该地区的重要水文观测站点之一。
历史上,该地区发生过多起较大规模的洪涝灾害事件,给当地经济和居民生活造成了严重影响。
因此,对于新安水文站长历时暴雨量频率的分析具有重要的现实意义。
2. 数据收集与处理为了进行历时暴雨量频率分析,我们搜集了新安水文站近50年来的历史降雨数据。
通过对数据进行整理和清洗,得到了每年的历时暴雨量数据集。
3. 频率分析方法为了确定历时暴雨量的频率特性,我们采用了经验公式法进行分析。
根据经验公式,我们对历时暴雨量进行了排序,并计算了各个历时下的频率。
4. 结果与讨论根据频率分析的结果,我们得出了新安水文站的历时暴雨量频率特性。
通过对数据的统计和分析,我们发现在历时较短的情况下,暴雨量频率较高,而随着历时的增加,暴雨量频率逐渐减小。
这一结果与我们的预期相符合,也说明了该地区发生暴雨的规律。
5. 防洪减灾建议基于历时暴雨量频率分析的结果,我们提出以下防洪减灾建议:- 完善排水系统:加大对排水设施的投入,提高排水能力,以应对短时大雨造成的内涝问题。
- 加强堤防建设:加固现有的堤防,提高防洪能力,减少洪水对农田和居民区的侵袭。
- 持续监测预警:加强对气象和水文数据的监测,及时发布预警信息,提醒居民做好防洪准备。
- 加强科学研究:通过开展更多的研究和科学实验,提高对暴雨天气形成机制的认识,并寻找更有效的防洪减灾手段。
6. 总结本文对新安水文站长历时暴雨量频率进行了详细分析,得出了有关暴雨量发生频率的数据和结论。
这对于制定和改进防洪减灾措施具有一定的参考价值。
同时,我们也认识到频率分析只是对历史数据的统计和归纳,对未来的暴雨情况无法进行精确预测。
水文频率计算拟合度水文频率计算是流域水文学的一项重要研究内容,通过对历史水文数据进行统计分析,可以得出不同概率的洪水或干旱事件的发生频率,为流域防洪和水资源管理提供科学依据。
而水文频率计算的核心问题就是如何确定概率分布模型以及模型参数的拟合度,本文将就这一问题进行探讨。
一、概率分布模型的选择水文频率计算基于概率分析思想,选择适当的概率分布模型是关键。
常用的概率分布模型包括正态分布、对数正态分布、皮尔逊三型分布、广义极值分布等。
一般来说,根据观测数据的分布特征选择合适的概率分布模型,可通过对数据进行直方图分析、QQ图、PP图等图表方法进行判断。
如果数据分布接近正态分布,则适合使用正态分布模型;如果数据分布偏左,则可以考虑使用对数正态分布模型;如果数据分布呈现单峰或双峰,而且峰值在中心,则可以考虑使用皮尔逊三型分布模型;如果数据分布呈现右偏或左偏,而且峰值靠边,就需要选择广义极值分布模型等。
二、概率分布模型参数的拟合度概率分布模型的拟合度直接关系到水文频率计算结果的准确性,所以在确定概率分布模型之后,就需要进一步确定模型参数的拟合度。
目前,比较常用的方法包括极大似然估计法、贝叶斯推断法、矩估计法等。
1. 极大似然估计法极大似然估计法是一种经典的参数估计方法,简单易行,而且适用范围广。
该方法的核心是最大化似然函数,使其等于实际观测值的概率。
具体来说,就是根据观测数据,推导出满足该数据分布的最大似然函数,找到最优参数组合,从而得到概率分布模型的参数。
常见的方法包括Box-Cox变换、L-曲线、最大似然估计法等。
2. 贝叶斯推断法贝叶斯推断法基于贝叶斯定理,将模型参数视为一个随机变量,其分布反映了参数取值的不确定性。
在求解模型参数时,需要利用先验知识,通过对后验分布进行采样取得模型参数。
相对于极大似然估计法来说,贝叶斯推断法更加灵活,可以处理数据不均匀、缺失、重复等问题。
3. 矩估计法矩估计法是一种非常简单的参数估计方法,其核心是利用样本矩去逼近理论矩,确定概率分布模型的参数。
水文频率分析方法hydrologic frequency analysis(讲座)(一、问题;二、原理;三、步骤;四、应用;五、讨论)一、问题高等学校的“培养人才、发展科学、服务社会”的功能。
其中的培养人才的功能:把所学课程的知识逐步遗忘,最后未被遗忘的知识,对最后未被遗忘的知识的认识、运用和创新。
“水文频率分析方法”,就是我认为的《水文学》课程中这种很可能最后未被遗忘的知识。
各门自然科学是人类对大自然各种现象(“文”)的系统知识,大自然各种现象之间本身具有普遍的联系。
若各门自然科学的各个知识点看作水分子,则这些知识点象水文循环一样,也在各门自然科学之间运动、更新,把各门自然科学联结成一个整体上的科学。
20世纪30年代普郎克:“科学是内在的整体,实际上存在着从物理到化学,通过生物学和人类学到社会学的连续链条,这是任何一处都不能打断的链条。
目前整体上的科学,被分解为各门科学,不是取决于自然现象本身,而是取决于人类认识能力的局限性、阶段性。
”[工程水文学主要包括水文计算、水文预报和水利计算三个组成部分。
水文计算主要运用概率论和数理统计的原理和方法,对未来长期的水文情势作出概率预估,为各类水利工程的规划和设计提供设计暴雨、设计洪水设计年径流及其他有关水文数据。
水文预报是根据流域暴雨洪水形成理论和河道洪水波传播的规律,为各类防洪工程发布洪水预报;同时,也根据水体热量平衡原理,对山区融雪径流,河流、水库、湖泊冰情作出预报;根据土壤中水分的补给、运动和消退规律,为农业提供土壤水分的预报;根据河道退水规律,为航运和引水工程等作出枯季径流及其水位预报。
水利计算是研究水资源综合利用中的规划和经济效益论证,管理运用中的优化调度和对环境影响评价的理论、原则和计算方法,特别是水资源开发利用中系统分析的理论和方法。
]已学教学内容的总结研究对象:文—自然现象—水文现象(水文循环过程中的降水、蒸发、入渗、径流自然现象,活跃在地面以上平均约11公里的大气对流层顶至地面以下1~2公里深处的广大空间;全球每年约有577000立方公里的水参加水文循环,水文循环的内因,是水在自然条件下能进行液态、气态和固态三相转换的物理特性,而推动如此巨大水文循环系统的能量,是太阳的辐射能和水在地球引力场所具有的势能)—水文随机现象。
研究方法:水文随机现象—水文随机变量—水文随机变量的概率分布(确定一个普通变量,只要指明该变量取何值即可;确定一个随机变量,必须同时指明该随机变量取何值以及取该值的概率)—水文随机变量的各种统计特征。
研究问题:计算径流(设计年径流及设计年径流的年内分配过程);设计枯水(设计流量历史曲线,设计枯水流量);设计洪水(设计洪峰流量,设计洪水过程线)。
[总结为同一类问题—水文统计的基本问题]:建设各类水利水电、土木建筑等工程,需要为其提供一定设计频率p的水文设计值x p,p=P(X≥x p),例如:95%的设计年径流量y95%,1%的设计年最大洪峰流量Q m,95%。
思路:水文随机变量的概率分布 水文随机变量的各种统计特征,引出2个问题:1)概率分布的模型结构形式如何确定?2)概率分布模型结构中的参数如何确定?已学教学内容的总结研究对象:文—自然现象—水文现象(水文循环过程中的降水、蒸发、入渗、径流自然现象,活跃在地面以上平均约11公里的大气对流层顶至地面以下1~2公里深处的广大空间;全球每年约有577000立方公里的水参加水文循环,水文循环的内因,是水在自然条件下能进行液态、气态和固态三相转换的物理特性,而推动如此巨大水文循环系统的能量,是太阳的辐射能和水在地球引力场所具有的势能)—水文随机现象。
研究方法:水文随机现象—水文随机变量—水文随机变量的概率分布(确定一个普通变量只要指明该变量取何值即可;确定一个随机变量,必须同时指明该随机变量取何值以及取该值的概率)—水文随机变量的各种统计特征。
研究问题:计算径流(设计年径流及设计年径流的年内分配过程);[水文循环是自然界最重要的物质循环,它成云致雨,影响着一个地区的气候和生态,塑造地貌和实现地球化学物质的迁移,像链条一样连结着全球的生命,为人类提供不断再生的淡水资源和水能资源。
水文循环使我们生活的星球变得生机勃勃。
倘若没有水和水文循环,我们的星球会像月球一样,是一幅没有生命,寂静荒漠的图景。
][水文频率分析方法的定义]:根据某水文现象的统计特性,利用现有水文资料,分析水文变量设计值与出现频率(或重现期)之间的定量关系。
[目前常用的方法就是通过反复调整具有一定广泛适用性的皮尔逊III型频率曲线的三个统计参数x、v C和s C,从中确定与经验累积频率曲线吻合较好的理论频率曲线,此时的三个统计参数值作为最终参数估计值,并根据这些参数值和设计频率标准P推求水文随机变量的设计值。
]二、原理1 确定概率分布的模型结构形式。
试验:人们对某类自然现象进行观测、调查或实验等活动。
随机事件:在一定条件下所有可能发生、也可能不发生的试验结果。
要完全描述一个随机事件,必须既要描述该事件所取的具体试验结果,又要描述这些结果发生的可能性。
随机变量:随机事件各次试验结果的实数值变量。
随机变量的总体:随机变量可以取的所有试验结果实数值的全体。
水文现象一般都是随机现象;人们对其进行观测、调查或实验等活动所得的结果就是水文随机事件(例如第三章中的各种水文信息的采集过程:主要通过沿河布设水文站网,长期观测水文要素;水文调查,了解流域自然地理条件、历史洪水、枯水情况和人类活动;室内和野外实验,特别是对实验流域和代表性流域上的水文要素进行观测;成因分析;数理统计分析;地理综合法等方式、方法获取水文信息),可以用水文随机变量表示,应用数理统计学的理论和方法研究水文随机现象。
[历史:约于1880~1890年,美国的Herschel和Rafter首先应用了频率曲线(当时称为历时曲线)。
1896年,Horton把频率分析法用于径流研究中,多为正态分布的应用,把概率论和数理统计的理论、方法引入了水文学。
1914年Hazen第一次用正态机率格纸选配频率曲线;1924年Foster完整地提出了P-III型频率曲线的分析方法,制成了离均系数Φ值表,给频率计算带来了方便,并得到广泛应用。
这些贡献使水文变量与它们出现的概率联系起来,为制定工程设计标准和推求指定设计标准下的水文变量奠定了基础。
水文频率分析法及其应用已有百年左右的研究历史。
我国自20世纪50年代开始,在水文频率分析工作中,吸取各国经验但不宥于这些经验,参照国外有关规范但不死搬这些规范,创造性地做了大量分析研究,不仅在理论探讨上、处理方法上、同实际资料的拟合验证上以及对成果的合理性分析上都做出了出色的贡献,形成了一套符合中国实情的、能基本上解决实际问题的理论和方法。
]设X为一随机变量,x为任意实数,则P(X≥x)表示“随机变量X≥x”这一随机事件出现的概率。
当x取不同值时,(X≥x)代表不同的随机事件,因而相应的概率P(X≥x)也不同。
因此概率P(X≥x)是随x的改变而变化的一个普通实数值函数,若记该函数为F(x)=P(X≥x) (3-7) 则F(x)称为随机变量X的概率分布函数,它表示随机变量X落在区间[x, ]上的概率。
在水文学中,概率分布函数又称为频率曲线。
独立随机变量X的各种统计特征,都可以从它的概率分布函数F(x)= P(X≥x)中获得,概率分布函数完整地描述了随机变量的统计规律性。
[频率曲线实际上是一种样本系列分布统计规律表达形式的模型,是一种外延或内插的频率分析工具。
]水文随机现象、水文随机事件、水文随机变量、水文随机变量的总体、水文随机变量的概率分布;都是对同一研究对象(水文现象)的不同表达形式,实质上它们之间是相互等价的。
用水文随机变量X 的样本系列{nx x x ,...,,21},估计X 的概率分布函数(频率曲线)。
水文随机变量的概率分布函数,一般取皮尔逊三(P-III )型分布曲线,它的分布密度曲线为(当然也可以考虑用多项式拟合经验频率点数据,但物理解释缺乏)10)()()()(0----Γ=αβααβa x e x f a x 其中:⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫==⎪⎪⎭⎫ ⎝⎛-==Γ⎰∞--s v s s v x C C x C C C x a dx e x 2421)(2001βααα P-III 型分布曲线是(负)指数函数A x e A/1-和幂函数B Ax (取对数就成为直线关系,P.202-3)的耦合形式。
概率分布函数的统计物理解释:只要存在随机性,信息熵最大的概率分布函数就是稳定的、最可能发生、最常见的概率分布函数,这就是最大信息熵原理。
P-III 型分布曲线这种耦合分布形式,实质上假定了水文随机变量X -a 0的算术平均值∑--))((00a x a x p i i (气候条件整体不变)和几何平均值)(00)(a x p i i a x --∏(X 的相对变化量的算术平均值为常数)为常数:10100))(()(C a x a x X P a X E i n i i =--==-∑=,21000)ln()()ln(C a x a x X P a X E ni i i =--==-∑=(负)指数函数分布反映了变量的总和守衡的各种最随机现象(变量值取越小的概率越大,当地气候条件在一定时期内不变化),例如:全球大气的风速,日降水量,无雨期长度,一场降雨过程的总降雨量在流域上的空间分布,区域总收入在区域人口中的分配(需要增加适当的社会新约束条件,提高社会公平的程度),气体分子的能量分布(麦克斯韦—玻尔兹曼分布)。
水文随机现象⇔水文随机事件⇔水文随机变量⇔水文随机变量的总体⇔水文随机变量的概率分布⇔水文随机变量的各种统计特征幂函数分布反映了统计相似的各种最随机现象(X 的相对变化量的总和守衡:分形(B. B. Mandebort );例如径流过程和洪水过程的分配形式具有一定的稳定性,因此可以用代表年法和典型年法推求设计径流过程和设计洪水过程),例如:Horton 河流地貌律,月球上不同直径x 的陨石坑的出现概率f (x )。
由于P-III 型分布曲线既可以描述服从负指数函数分布的自然现象,又可以描述服从幂函数分布的自然现象,目前我国水文设计规范规定,水文随机变量的概率分布函数,一般取P-III 型分布曲线。
国内外大量水文设计实践也表明该分布符合实际。
这说明,除了算术平均值守衡和几何平均值守衡以外,再也没有其它的力量约束着水文随机变量。
[问题:大自然的各种随机现象,其演化机制,很可能就是这些现象所隐含的不同的守衡形式。
例如,质量守衡机制,能量守衡机制,质量-能量守衡机制E =mc 2;信息守衡机制;质量-能量-信息守衡机制?;…]2 确定P-III 型分布曲线的参数。