下载文档原格式
七年级等式的性质知识点等式是数学中重要的概念之一，在学习等式的过程中，我们需要了解等式的性质及其应用。
本文将从七年级等式的性质和重要应用方面进行介绍。
一、等式的基本概念1.等式的定义“等式”是指左右两边相等的式子，可用“=”号连接。
等式中的每个元素都称为“等式的项”。
例如：2x+3=5x-4在这个等式中，2x+3和5x-4分别是等式的两个项。
2.等式的意义等式是表示两个数相等的语句。
在求解问题的过程中，可以使用等式，将问题说明成两个数相等的形式。
等式可以让我们快速地计算出未知量，方便解决复杂的问题。
例如：小明的三倍加4等于19，即3x+4=19，可以解得出小明的值为5。
二、等式的性质1.等式的对称性等式的两边可以互换位置，等式仍然成立。
例如：a+b=b+ax+y=y+x2.等式的传递性如果a=b，b=c，则a=c。
例如：如果x+2=5，5-2=x，则x=3。
3.等式的合并性将两个等式左右两边相加或相减，等式仍然成立。
例如：x+3=7x+2=5两式相加得到 2x+5=124.等式的分配性将等式左右两边各乘以同一个数或者除以同一个不等于0的数，等式仍然成立。
例如：x+2=5两边同时减2得到x=35.等式变形将等式中的某一项移到另一边去，改变项的符号，等式仍然成立。
例如：x+5y=12变形得到x=12-5y三、等式的应用1.解方程等式可用来解方程，通过变形等式，求得未知数的值。
例如：x+2=8，通过变形等式得出x=6。
2.检验答案在解决数学问题时，可以通过等式来检验答案是否正确。
例如：小朱有20个苹果，小华有30个苹果，他们两人比较苹果的数量时，可以使用等式20+30=50来检验答案是否正确。
3.化简式子等式可以用于化简式子，将式子变形为更简单的形式。
例如：3(x+2)=3x+6，可以化简为3x+6=3x+6，从而进一步化简。
总结：等式是数学中很重要的概念之一，学习等式的性质有助于我们解决数学问题。
掌握等式的基本概念、等式的常见性质以及等式的应用方法，可以帮助我们更好地理解各种数学公式、定理和算法。
数学等式的定义和性质第一部分：等式的定义：含有等号的式子叫做等式(数学术语)。
形式：把相等的两个数(或字母表示的数)用“=”连接起来。
等式可分为矛盾等式和条件等式。
矛盾等式就是左右两边不相等的"等式"。
也就是不成立的等式,比如5+2=8,实际上5+2=7,所以5+2=8是一个矛盾等式.有些式子无法判断是不是矛盾等式,比如x-9=2,只有x=11时这个等式才成立(这样的等式叫做条件等式),x11时,这个等式就是矛盾等式。
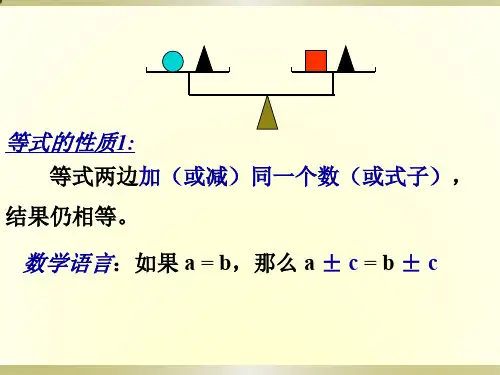
第二部分：等式的性质：1.等式两边同加上(或减去)同一个数或同一个整式，所得结果仍是等式。
即若a=b，则am=bm。
2.等式两边同乘以(或除以)同一个数(除数不能为零)，所得结果仍是等式。
即若a=b，则am=bm，(m0)。
3.等式具有传递性。
若a1=a2,a2=a3,a3=a4,……an=an,那么a1=a2=a3=a4=……=an4.等式两边同时乘方(或开方)，两边依然相等若a=b 那么有a^c=b^c 或(c 次根号a)=(c次根号b)5.等式的对称性(若a=b，则b=a)。
等式的性质是解方程的基础，很多解方程的方法都要运用到等式的性质。
如移项，运用了等式的性质1;去分母，运用了等式的性质2。
运用等式的性质，涉及除法时，要注意转换后，除数不能为0，否则无意义。
拓展：1：等式两边同时被一个数或式子减，结果仍相等。
如果a=b，那么c-a=c-b2：等式两边取相反数，结果仍相等。
如果a=b，那么-a=-b3：等式两边不等于0时，被同一个数或式子除，结果仍相等。
如果a=b0，那么c/a=c/b4：等式两边不等于0时，两边取倒数，结果仍相等。
如果a=b0，那么1/a=1/b第三部分：例题：方程3x-4=1+2x，移项，得3x-2x=1+4，也可以理解为方程两边同时()A.加上(-2x+4)B.减去(-2x+4)C.加上(2x+4)D.减去(2x+4)已知：|a|=3，b2=4，ab0，求a-b的值.解答过程：根据等式的基本性质1，方程3x-4=1+2x的两边同时加上(-2x+4)，可得：3x-4+(-2x+4)=1+2x+(-2x+4)，即3x-2x=1+4.故选A.。
利用等式的性质解方程的几点思考
打开五年级上册的数学教材一看，第五单元就是解方程，仔细一看内容，和我小时候所学的用四则运算关系解方程截然不同。
以前也听过五年级的数学老师讲过，用等式的性质解方程太复杂了，总觉得还是原来依据四则运算关系解方程，便于教、便于学。
本文仅就与此相关的一些问题，谈谈个人的有关认识与体会。
一、新课程为什么要用等式的基本性质解方程
过去，在小学教学解方程，依据的是四则运算之间的关系，如“加数=和-另一个加数”，“因数=积÷另一个因数”．等等。
由于这些关系小学生在学习加减法、乘除法时．早就不断有所感知，积累了比较丰富的感性经验，所以到小学中高年级再加以概括就显得水到渠成，运用这些关系解未知数只出现在等式一边的简易方程也比较自然。
但是，这种“算术”的解方程思路毕竟走不了多远，一到中学就被彻底抛弃，取而代之的是等式的基本性质。
而且小学依据四则运算关系解方程教得越多，练得越巩同，初中方程教学的负迁移就越明显，入门障碍就越大。
既然一到中学就被取代，并将彻底遗忘．为什么就不能改变，寻找一条新的可持续发展的出路呢?
现在，为了减少过渡性的、很快被淘汰的知识，为了避免中小学数学教学各自教一套，避免中学“另起炉灶”，为了促进学习的正迁移，将等式基本性质作为小学解方程的依据，使中小学解方程的思路得到基本统一，解释趋于一致。
这是一项很有意义的改革，值得我们
为之尝试、探索，积累经验。
通过实践还进一步发现，以等式基本性质为依据，有利于凸显等量关系，有助于渗透初步的方程思想和初步的数学建模思想。
这些则是改革初衷之外的收获了。
二、利用等式的性质解方程的一些困惑
利用等式的性质解方程，对于小学数学教师来说需面对并妥善解决一系列的教学实际问题。
只知道要过河，如果没有可操作的过河方法，仍然无济于事。
1．如何理解“等式的基本性质”?
新课程下的小学数学概念性的东西不多，一般都是在例题中或者练习中依靠学生自己归纳总结，而新教材对于等式的基本性质确实给出了明确的解释（见小学数学五年级上册第64页和第65页），对于这一性质，有的老师将其称为“天平原理”或者“天平平衡原理”，这都是可行的，学生理解起来也相对形象一些。
2、如有学生运用四则运算的关系解方程怎么办？
初学解方程时我一直要求学生利用等式的基本性质，但有些聪明的同学却能利用四则运算的关系来解方程。
比如，在教学解方程例1：X+3=9时，如果利用等式的性质就应该这样解：X+3-3=9-3解得X=6，讲到这个地方，班上有个同学就说：“老师，我有更简单的方法。
”我问：“你用的什么方法？”他说：“在X+3=9中，X是一个加数，加数=和-另一个加数，所以X=9-3，解得X=6，比你刚才讲的方法简单多了。
”他一说到这个地方，其他的同学也跟着附和，赞同他的方法而
否定用等式的性质解方程。
还比如，在教学例3:20-x=9时，用等式的性质解是这样的：
20-x = 9
解： 20-x+x = 9+x
20 = 9+x
9+x = 20
9+x-9 = 20-9
x = 11
而有的同学说这样太麻烦了，所以就出现了下面这种解法：
20-x = 9
解: x = 20-9
x = 11
这样做的学生说：在这个方程里，x是减数，减数=被减数-差，这样解比用等式的性质解方便多了.
面对这种情况，当时也就只是一再强调必须用等式的性质来解，而没有讲清理由，所以那节课后学生的作业基本上都是用的四则运算的关系解的方程。
后来，我请教以前上过这个知识的老师，也翻过《小学数学新课程标准》，因此我就给学生讲解：运用四则运算间的关系解方程，是可以的，但应该根据教材突出用等式性质解的思考方法为宜。
同时，给学生强调新的思考方法以后到中学解更复杂的方程时一直有用，以提高学生学习掌握根据等式基本性质解方程的积极性。
三、利用等式的性质解方程的一些教学策略
1．初学解方程，学生不习惯运用等式的基本性质时
首先，教学等式基本性质时，可以安排一些口答练习，如：b÷3=45÷3，b=( )，以便从一开始就尽可能地帮助学生初步体会等式基本性质的优势，逐步熟悉依据等式基本性质解方程的思路。
其次，教学解方程时，可以先通过复习，让学生再现、复述等式基本性质的内容，为新授作好铺垫；给出例题后，再用天平的教具或者图示表示例题的方程；同时通过明确的指导语予以思维定向．如“从今天起，我们将学习怎样用天平保持平衡的道理来解方程”。
这些都是行之有效的措施，一般来说，会有学生想到运用等式的基本性质来解方程。
由于教材在设计例题时，为了直观，选用的数据都比较小．学生一眼就能看出方程的解。
这时要求学生说出解方程的根据，显得有些“画蛇添足”。
这里，我们可以通过练习，如x+34=87，x-23=66，5x=50．x ÷7=43等，让学生说说，哪几题是在方程两边加上或减去一个数，哪几题是在方程两边乘或除以一个不等于零的数，从而使学生初步体会用天平保持平衡的道理来解方程思路比较统一的优点。
还可以告诉学生，以后进一步学习解更复杂的方程时这一优势会更加明显。
2．解决实际问题，学生列出形如a-b=x与b÷a=x的方程时这是列方程解决实际问题时学生经常会出现的现象。
对此，常用的对策有两条。
其一，引导学生根据题意，将可用加减法表示的等量关系统一成用加法表示的等量关系；将可用乘除法表示的等量关系统一成用乘法表示
的等量关系。
例如，路程÷速度=时间，路程÷时间=速度，可以归结为速度×时间=路程。
有些教师顾虑这是不是有违“算法多样化”的精神，其实这种顾虑是对课改理念的误读。
首先，同一等量关系的不同表达形式，常常并无本质差异：其次，一题多解与多题一解，算法多样化与算法优化，发散思维与收敛思维，都是相辅相成的，不应偏废。
而且，这里的收敛思维、多题一“式”，恰恰体现了列方程解决问题思路统一的特点，是必须让学生初步感悟、有所体会的。
其二，如果学生感兴趣，也可引导他们自己尝试解形如a-x=6与a=6的方程。
试举一例：王老师买了5支同样的钢笔付143元，找回1 8元．求钢笔的单价。
学生设钢笔每支x元，得143一5x=18或者(143—18)÷x=5。
怎么解呢?不妨联想天平，两边盘子内的物品交换一下，天平仍然平衡．得18=50—2x或2=(50—18)÷x，等式两边同加2x 或同乘x，得18+2x=50或2x=50—18。
有的教师把“等式两边交换”比喻为“挑担换肩”，农村的孩子有这样的生活经验，一听也就明白了。
虽然学生能用四则运算的关系解方程，但教师必须强调，为了给中学学代数打下基础，尽量要用等式的性质来解方程。
总之，新课程提倡用等式的性质解方程，思路更统一，我们应正确看待解方程方法的改变，提倡用新的方法来引领学生。
