高斯光束下的圆屏衍射

高斯光束照射下的圆盘衍射
高斯光束照射下的圆盘衍射
基于圆孔光阑函数展开为复高斯函数和的方法,用Colins积分公式,导出了高斯光束照射下圆盘衍射的光场近似解析表达式,经计算机数值计算,对高斯光束照射下圆盘衍射的衍射特性进行了详细的分析.
作者：李汝烯环敏李茂琼 LI Ru-xi HUAN Min LI Mao-qion 作者单位：大理学院,物理与电子信息学院,云南,大理,671003 刊名：昆明理工大学学报（理工版）ISTIC PKU英文刊名：JOURNAL OF KUNMING UNIVERSITY OF SCIENCE AND TECHNOLOGY （SCIENCE AND TECHNOLOGY）年，卷(期)：2007 32(5) 分类号：O4-34 关键词：高斯光束 Colins积分光衍射。

实验三 高斯光束的透镜变换实验一 实验目的1.熟悉高斯光束特性。

2.掌握高斯光束经过透镜后的光斑变化。

3.理解高斯光束传输过程.二 实验原理众所周知，电磁场运动的普遍规律可用Maxwell 方程组来描述。

对于稳态传输光频电磁场可以归结为对光现象起主要作用的电矢量所满足的波动方程。

在标量场近似条件下，可以简化为赫姆霍兹方程，高斯光束是赫姆霍兹方程在缓变振幅近似下的一个特解，它可以足够好地描述激光光束的性质。

使用高斯光束的复参数表示和ABCD 定律能够统一而简洁的处理高斯光束在腔内、外的传输变换问题。

在缓变振幅近似下求解赫姆霍兹方程，可以得到高斯光束的一般表达式：()222()[]2()00,()r z kr i R z A A r z e ez ωψωω---=⋅ （6）式中，0A 为振幅常数；0ω定义为场振幅减小到最大值的1e 的r 值，称为腰斑，它是高斯光束光斑半径的最小值；()z ω、()R z 、ψ分别表示了高斯光束的光斑半径、等相面曲率半径、相位因子，是描述高斯光束的三个重要参数，其具体表达式分别为：()z ωω= （7）000()Z z R z Z Z z ⎛⎫=+ ⎪⎝⎭（8）1ztg Z ψ-= （9） 其中，200Z πωλ=，称为瑞利长度或共焦参数（也有用f 表示）。

（A ）、高斯光束在z const =的面内，场振幅以高斯函数22()r z e ω-的形式从中心向外平滑的减小，因而光斑半径()z ω随坐标z 按双曲线：2200()1z zZ ωω-= （10）规律而向外扩展，如图四所示高斯光束以及相关参数的定义图四（B ）、 在（10）式中令相位部分等于常数，并略去()z ψ项，可以得到高斯光束的等相面方程：22()r z const R z += （11） 因而，可以认为高斯光束的等相面为球面。

（C ）、瑞利长度的物理意义为：当0z Z =时，00()2Z ωω=。

在实际应用中通常取0z Z =±范围为高斯光束的准直范围，即在这段长度范围内，高斯光束近似认为是平行的。

高斯光束的微圆孔衍射变换的计算及其仿真常山;桑志文;吴波;毛杰健【摘要】由菲涅尔-基尔霍夫衍射公式得到高斯光束的微圆孔衍射的积分式,推导了该积分式的数值算法和解析算法,用Matlab软件进行了仿真实验研究高斯光束的微圆孔衍射变换,有助于激光束衍射实验及其测控理论与技术的研究.【期刊名称】《江西师范大学学报（自然科学版）》【年(卷),期】2010(034)005【总页数】5页(P511-515)【关键词】高斯光束;圆孔衍射变换;光强分布;数值计算;解析计算;仿真实验【作者】常山;桑志文;吴波;毛杰健【作者单位】上饶师范学院,物理与电子信息学院,江西,上饶,334001;上饶师范学院,物理与电子信息学院,江西,上饶,334001;上饶师范学院,物理与电子信息学院,江西,上饶,334001;上饶师范学院,物理与电子信息学院,江西,上饶,334001【正文语种】中文【中图分类】O436.1;TN241在激光应用中对激光的模式、波面、发散角、光强分布以及光斑的形状与大小有很多的要求,因此需要对它进行测量和控制[1-2].高斯光束的微圆孔衍射变换在激光束测控、微光学以及微光机电技术中有着重要作用[3-4].虽然有不少文献对高斯光束的圆孔衍射进行了研究[5-7],但仍需要用不同的方法从不同的角度加以研究.为此,本文研究高斯光束的微圆孔衍射变换的计算并进行仿真实验.1.1 高斯光束的微圆孔衍射变换的积分式如图1所示,设z′=z-z0,波长为λ、束腰位于P(0,0,z0)且腰半径为w0的基模高斯光束可表示为[1]由于高斯光束发散角很小,在入射微圆孔时倾斜因子对振幅的影响很小,可以取为1.对平面衍射屏有cos(n,s)=-z1/s,s为点Q(x,y,0)处的次波面元dσ到点P(x1,y1,z1)的距离.根据菲涅尔-基尔霍夫衍射公式,由(2)式可以得高斯光束照射微圆孔屏∑衍射在极坐标x+jy=ρejθ下的积分式[8]1.2 高斯光束的微圆孔衍射变换的计算1.2.1 一种数值算法(4)式难以直接积分,根据微积分“先细分再求和”的思想,将圆孔半径R分为N个微元Δρ=R/N,有ρ=nR/N,周角2π分为M个微元Δθ=2π/M,有θ=2πm/M,可得一种数值计算方法为[9-11]利用Matlab软件计算模拟图1所示的波长为λ、束腰在P0(0,0,z0)且腰半径为w0的基模高斯光束,通过半径为R的微圆孔屏的衍射变换的情况,对算法进行验证和分析,并且讨论影响高斯光束微圆孔衍射变换的因素.2.1 算法验证与分析实验1 由(3)式计算高斯光束入射微圆孔的光强分布,分别由(5)、(7)和(8)式计算高斯光束通过微圆孔衍射变换后的光强分布.λ=0.5μm、束腰在P0(0,0,-10 mm)且腰半径w0=0.1 mm的基模高斯光束,通过半径R=10μm的微圆孔屏在不同距离z1处的衍射变换的光强分布.图2表明数值计算(5)式可以计算高斯光束通过微圆孔的不充分衍射变换、菲涅尔衍射变换和夫琅禾费衍射变换,如果增加分割微元数M和N,会大大提高计算的精度,获得更好的仿真效果,但是运算速度较慢.图3表明,解析(7)式可以计算高斯光束通过微圆孔的菲涅尔衍射变换和夫琅禾费衍射变换,精度跟(5)式接近,而运算速度增快很多.但是图3(a)跟图2(a)相比较有很大差异,可见取了菲涅尔近似的解析(7)式不能计算高斯光束通过微圆孔的不充分衍射变换.图4(c)表明,解析式(8)可以计算高斯光束通过微圆孔的夫琅禾费衍射变换,精度跟(7)式接近,而运算速度会更快;从图4(b)可见取了夫琅禾费近似的(8)式也能够近似计算高斯光束通过微圆孔的菲涅尔衍射变换,说明kρ2/z1≪π对高斯光束的微圆孔衍射变换的影响不大.但是从图4(a)跟图2(a)相比差异极大,可见解析式(8)不能计算高斯光束通过微圆孔的不充分衍射变换.3.2 衍射变换的影响因素实验2 由解析式(7)计算z1=5 mm时基模高斯光束通过微圆孔衍射变换的光强分布,每次只改变实验1中的一个参数:束腰位置变为P0(0,0,-10 000 mm)、束腰半径变为w0=1 mm、波长变为λ=0.9μm、圆孔半径变为R=8μm.图5(a)跟图3(b)对比,束腰位置由P0(0,0,-10 mm)变为P0(0,0,-10 000 mm)时,衍射光强的分布变化得很微小;而图5(b)跟图3(b)对比,束腰半径由w0=0.1 mm变为w0=1 mm,衍射光强的分布也变化得很微小.这体现了高斯光束的发散角很小,平行性胜于球面波而接近平行光的优点.图5(c)跟图3(b)对比,波长由λ=0.5μm变为λ=0.9μm,衍射光强的分布变化得很大.波长和孔径的大小越接近,相位稳定所需要的距离z1就越短,衍射场的空间分布就会越细密.图5(d)跟图3(b)对比,孔半径由R=10μm变为R=8μm,衍射光强的分布变化得也很大.衍射孔径越小,相位稳定所需要的距离z1就越短,衍射场的空间分布就越细密,这有利于发展微光学工程.本文研究了高斯光束的微圆孔衍射变换的计算方法并进行了仿真实验,(5)、(7)和(8)式可以有效而可靠地计算各自条件下的高斯光束微圆孔衍射变换的情况.可见,菲涅尔-基尔霍夫衍射理论作为典型的标量衍射理论,能够很好地计算衍射屏尺寸为数十至数百倍波长时的衍射现象.衍射屏的尺寸接近光波长时,高斯光束通过微圆孔的夫琅禾费衍射变换和菲涅耳衍射变换的光场分布非常细密而稳定.如果通过振幅和相位调制可以获得所需要的衍射场,应用于激光光波工程中调控高斯光束的传输与变换,这也为微孔板、微透镜和光耦合器等微光学器件以及微光机电技术奠定一定的理论基础.【相关文献】[1] 吕百达.激光光学:光束描述、传输变换与光腔技术物理 [M].3版.北京:高等教育出版社,2003:1-196.[2] 左铁钏.制造用激光光束质量、传偷质量与聚焦质量 [M].北京:科学出版社,2008:19-101.[3] 杨国光.微光学与系统 [M].杭州:浙江大学出版社,2008:1-29.[4] 张长水,杨小琦,徐海斌,等.湍流对远场光束质量的影响 [J].江西师范大学学报:自然科学版,2009,33(5):582-586.[5] 李汝烯,白凤翔,李汝恒,等.高斯光束圆孔衍射特性 [J].云南师范大学学报:自然科学版,2008,28(2):40-44.[6] 周国泉,倪涌舟,王绍民.高斯光束经波长级圆孔衍射的轴上光强特性 [J].中国激光,2004,31(4):437-440.[7] 韩运侠,冯建武,赵志国.高斯光束通过透镜-微小圆形光辣系统的衍射 [J].江西师范大学学报:自然科学版,2009,33(6):683-686.[8] 马科斯·玻恩,埃米尔·沃尔夫.光学原理 [M].7版.杨葭荪,译.北京:电子工业出版社,2005:342-429.[9] 常山,桑志文,高志强.单色点源矩孔衍射的模拟与分析 [J].光学仪器,2009,31(2):68-71.[10] 常山,吴波,桑志文,等.点源圆孔衍射光场的计算 [J].江西科学,2009,27(6):816-819.[11] 杨兴,胡建明,戴特力.光纤光栅传感器的原理及应用研究 [J].重庆师范大学学报:自然科学版,2009,26(4):1-5.。

贝塞尔-高斯光束通过圆孔与圆环光阑的衍射屈军;孟凯;汪六三;丁培宏;崔执凤【摘要】为了研究贝塞尔-高斯光束通过圆孔硬边光阑和圆环光阑的衍射特性,从Collins公式出发,采用数值模拟的方法模拟出光强分布.模拟结果表明,贝塞尔-高斯光束经圆孔光阑衍射后轴上光强随菲涅耳数F呈周期振荡;贝塞尔-高斯光束经圆环光阑后轴上光强随F呈振动衰减.在F相同时,贝塞尔-高斯光束经圆孔光阑衍射后横向光强分布比经圆环光阑衍射后横向光强分布平滑,孔径越小,光强调制越明显;当孔径与束腰相等时候,横向光强分布与菲涅耳数没有关系.【期刊名称】《激光技术》【年(卷),期】2008(032)004【总页数】3页(P393-395)【关键词】激光光学;贝塞尔高斯光束;衍射;圆孔光阑;圆环光阑【作者】屈军;孟凯;汪六三;丁培宏;崔执凤【作者单位】安徽师范大学,物理与电子信息学院,芜湖,241008;安徽师范大学,物理与电子信息学院,芜湖,241008;中国科学院,安徽光学精密机械研究所,合肥,230031;安徽师范大学,物理与电子信息学院,芜湖,241008;安徽师范大学,物理与电子信息学院,芜湖,241008【正文语种】中文【中图分类】O435引言贝塞尔-高斯光束是一种有应用前景的光束，它在一定条件下呈现“无衍射”特性，对这种光束的研究引起人们的极大关注[1-10]。

LIU等人对贝塞尔光束及贝塞尔-高斯光束的传输和聚焦特性已做了详细的计算分析和实验研究进行了比较[5]；PAMELA,OVERFELT等人对贝塞尔-高斯光束经不同几何构形光阑的衍射作了比较研究[6-7]；JIANG等人计算了加光阑贝塞尔光束的空间频谱[8]。

作者就贝塞尔-高斯光束经圆孔光阑和圆环光阑衍射后光强分布随菲涅耳数F的变化作了研究，并对F相同时的横向光强分布，以及当孔径与束腰相等时的横向光强分布与菲涅耳数的关系作了比较，对进一步研究贝塞尔-高斯光束有理论和现实意义。

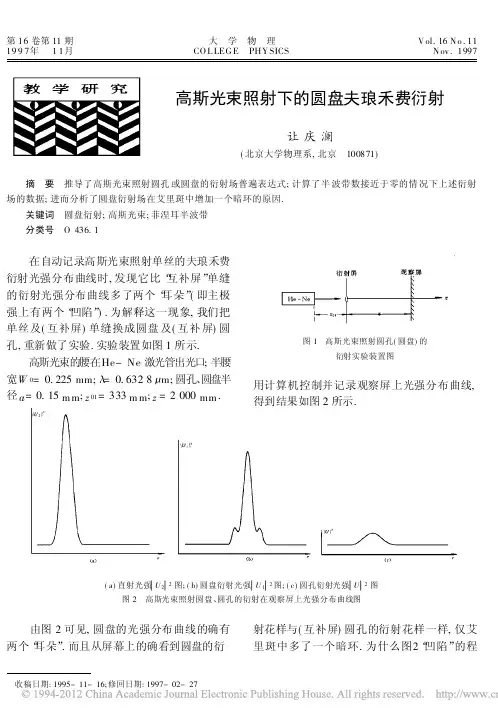
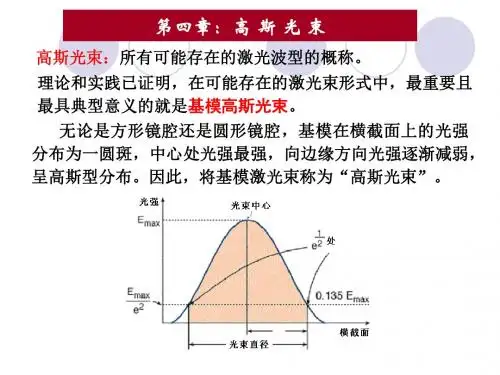
第16卷第11期大　学　物　理V ol.16N o.111997年　11月CO L LEG E PHY SICS N ov.1997　收稿日期:1995-11-16;修回日期:1997-02-27高斯光束照射下的圆盘夫琅禾费衍射让庆澜(北京大学物理系,北京　100871)摘　要　推导了高斯光束照射圆孔或圆盘的衍射场普遍表达式;计算了半波带数接近于零的情况下上述衍射场的数据;进而分析了圆盘衍射场在艾里斑中增加一个暗环的原因.关键词　圆盘衍射;高斯光束;菲涅耳半波带分类号　O 436.1 在自动记录高斯光束照射单丝的夫琅禾费衍射光强分布曲线时,发现它比“互补屏”单缝的衍射光强分布曲线多了两个“耳朵”(即主极强上有两个“凹陷”).为解释这一现象,我们把单丝及(互补屏)单缝换成圆盘及(互补屏)圆孔,重新做了实验.实验装置如图1所示.高斯光束的腰在He-Ne 激光管出光口;半腰宽W 0=0.225mm; =0.6328 m;圆孔、圆盘半径a =0.15m m ;z 01=333m m ;z =2000mm .图1　高斯光束照射圆孔(圆盘)的衍射实验装置图用计算机控制并记录观察屏上光强分布曲线,得到结果如图2所示.(a)直射光强 U 2 2图;(b)圆盘衍射光强 U 1 2图;(c)圆孔衍射光强 U 2图图2　高斯光束照射圆盘、圆孔的衍射在观察屏上光强分布曲线图 由图2可见,圆盘的光强分布曲线的确有两个“耳朵”.而且从屏幕上的确看到圆盘的衍射花样与(互补屏)圆孔的衍射花样一样,仅艾里斑中多了一个暗环.为什么图2“凹陷”的程度不历害?是否由U 2和U 的相位不同造成的?“耳朵”处相位究竟是多少?为探讨这些问题,我们用计算机来模拟高斯光束照射圆孔及圆盘的衍射实验.由菲涅耳-基尔霍夫衍射公式或瑞利-索末菲衍射公式,可得圆孔衍射场为U (P )=1i ∫∫U 2(Q )・ex p(i k ・P Q )PQcos(n ,PQ )d S式中:Q 点为圆孔面 上的任意点;P 点为衍射场的任意点;k =2 / ;n 为图1中z 轴反方向的单位矢量.由激光原理可知高斯光束表达式为U 2(P )=A 0W ex p -r 2W2・ exp i[k (z +z 01)-f n ]+i kr 22C r 式中:W =W 0[1+(z +z 01)2/z 2r ]1/2;C r =(z +z 01)[1+z 2r /(z +z 01)2];f n =tg -1[(z +z 01)/z r ];z r= W 2/ (叫瑞利距离);r 为场点P 到z 轴的距离;z 01、z 、z 轴的含义见图1.U 2(Q )的表达式可由高斯光束表达式得到.在旁轴近似条件下,令cos (n ,Q )≈1,可以得到U (r ,z )=a 2i z W 1∫10ex p -a 2b 2W 21ex p(i b 2H )・∫2 0exp (-i 2 bv ・cos (-1)db d b ;U 2(r ,z )=1Wexp-r 2W 2ex p i r 21C r-1z+f n 1-f n ;U 1(r ,z )=U 2(r ,z )-U (r ,z )以上三式中均已略去A 0ex p{i[k (z +z 01+r 2/2z )-f n 1]}因子,不影响它们之间的相互关系及光强分布曲线的形状.其中:H ≡H m +H n 是P 点面对衍射孔的半波带数;H m ≡a 2・1C r 1;H n ≡a 2 ・1z是P 点面对衍射孔的菲涅耳数;v≡ar / z ;W 1、C r 1、f n 1为z =0时的W 、C r 、f n ;r 1为衍射屏上Q 点到z 轴的距离;b ≡r 1/a .作者利用这些公式,对圆孔、圆盘衍射场的复振幅U (r ,z )≡u e i f 、U 1(r ,z )≡u 1e i f1及高斯光束直射场的复振幅U 2(r ,z )≡u 2e i f 2,用SGI 计算机(工作站)进行了计算,得到一批图及数据.现将其中一部分附上,并分析其含义.图3及图4分别是z 01=0及z r 时的图形.这两个图号各包括(a )、(b )、…、(i )9张小图.其中(a)、(b)、(c)三图是u 1≡ U 1(r ,z ) 、u ≡ U (r ,z ) 、u 2≡ U 2(r ,z ) 随r =0→12m m 而变化的图形(z =2000mm ;a =0.15m m );(d )、(e )、(f)三图是u 1min ≡ u 2-u 、d u 1≡u 1-u 1min 、d p ≡1-cos(f 2-f )随r =0→12mm 而变化的图形(z =2000mm ,a =0.15mm );(g )、(h)、(i)三图是f 1、f 、f 2随r =0→12mm 而变化的图形(z =2000mm ;a =0.15mm),其中f 1、f 、f 2是U 1、U 、U 2的相位.表1是高斯光束、衍射屏、衍射场点基本参数的数据表.表1　高斯光束衍射屏衍射场点基本参数表z 01HmH(1/C r -1/z )/mm -1W 1/mm 00.5629×10-60.1778×10-1-0.7773×10-50.2250z c0.7074×10-10.8851×10-1-0.6122×10-40.3180C r 1/mmf n 1/radW /mmC r /mmf n /rad0.6317×1080.3979×10-50.1805×100.2032×1040.1446×100.5027×1030.78470.2028×100.2279×1040.1460×10W 0=0.2250m m ;z r =0.2513×103mm ;a =0.1500mm ;z =0.2000×104mm;H n =0.1778×10-1.对这些图表进行分析,我们可以得出下列结论:1)图3、图4各小图中,(a )图u 1的曲线都在r >5m m 的区域和相应(b)图u 的曲线完全一样,而相应(c)图u 2的曲线在此区域为0.这就是在直射光为零的区域,互补屏的衍射花样完全一样(u 1=u )的意思.6大　学　物　理 第16卷 2)图3、图4各小图中,u1的曲线都在r< 5mm的区域与相应u的曲线不一样,u的曲线是一个单调、光滑曲线,而u1曲线则多了一个“凹陷”,即u1曲线多了“两个耳朵”.从衍射图样看,是在相应的艾里斑里面出现了一个暗环.由图还可见,这个“凹陷”以z01=0时最深(u1= 0),随着z01增大,“凹陷”越来越浅.3)u1曲线“凹陷”的成因有两个,一个是由于u1min有“凹陷”;另一个是由于d u1有“凹陷”.而u1=u1min+d u1,因而u1曲线的“凹陷”是这二者的综合效果.4)u1min曲线“凹陷”的形成规律比较简单.在高斯光束远场发散角W0<艾里斑发散角1.22・2a=0.610.15mm的条件下,因为当r由0逐渐增大至艾里斑的r时,u2由大于u逐渐变成等于u,而后又小于u;而在u2=u时,u1min ≡ u2-u =0,在u2>u或<u时,u1min>0,因此u1min在u2=u的r处(令此r为r0)有一极小值.z01增大时,u2曲线逐渐变宽,而u曲线宽度变化不大,u2=u的r(即r0)也逐渐变大.5)d u1曲线的“凹陷”形成规律较复杂.因为u21-u21min=2uu2d p,所以在u≠0及u2≠0区间,d u1≡u1-u1min=0的必要与充分条件是d p =0,而d p≡1-cos(f2-f)=0的必要与充分条件是f2-f=0.而由图可见(除图3中z01=0时以外)d p曲线及d u1曲线均在r=1.6mm附近某点为零,因此d u1曲线在此时有极小值,这个极小值点的位置取决于f2=f的位置.一般情况下,当r由0逐渐增大时(在r小于艾里斑的r以前),f的变化是很小的(见图3及图4的(g)、(h)、(i)三个小图),而f2的变化则较快,且z较大(即满足远1C r-1z→0,则f2基本上不随r变化,因而f2-f不随r变化,从而显不出“凹陷”来,此时只有u1min的“凹陷”能显现出来.在z01≠0时,1C r-1z≠0,z01越大,1C r-1z越大(详见表1),则这一个因素起的作用越大.总的“凹陷”将由两个因素综合作用来决定.这时由于u1=u1min+ d u1,所以不论u1在那一个r值(令=r4)的地方有一个(u1的)极小值,其数量u1(r4)总是≥u1min(r4),而u1min(r4)只有当r4=r0时才为0,r4离r0越远,u1min(r4)越大,因而u1(r4)形成的“凹陷”越浅.作者用上述模拟计算的结论为指导,回过头来又做了许多实验(包括用圆盘与用单丝的),结果与理论预期的完全一致.比如将图2中z01=333mm改为43m m(因所用激光器外罩尺寸及其他条件限制,无法再小了)得到的圆盘衍射光强分布曲线图两个“凹陷”就“到底”了(即u1(r4)=0).与图3(a)完全一致(此时z01= 0,H=0.018).总的来说,作者利用计算机模拟技术,提供了u、f、u1、f1、u2、f2等的系列数据,从而才有可能比较完整地分析与解释在z01接近于零时,圆盘夫琅禾费衍射光强分布曲线产生“耳朵”的现象.致谢　本文的工作得到北京大学计算中心“计算费基金”的支持.在此表示感谢.参考文献　1　杨之昌,王潜智,印榴贞.物理光学实验　上册.上海:上海科学技术出版社,1986.168～1712　顾德门J W.傅里叶光学导论.詹达三等译.北京:科学出版社,1979.503　陈怀琳,邵义全.普通物理实验指导(光学).北京:北京大学出版社,1990.163～179(下转23页)9第11期 让庆澜:高斯光束照射下的圆盘夫琅禾费衍射图2图3 本文的核心部分采用清华大学高炳坤教授的修改意见,谨致深深的谢意.参考文献1　夏学江等主编.波动与光学.北京:清华大学出版社,19882　蔡伯濂.力学教学研究.北京:北京大学出版社,1982.AN ANALYSIS OF THE FORMATION OF STATIONARYWAVE WITH PHASE DIAGRAMLuo Zhian Wan Shibao Chen Jiansong(A it F or ce Radar Co llege o f the Chinese P eople's L ibo ration A rmg ,W uhan ,430010,China )Abstract A phase diag ram o f a w ave is inv ented,it is a mov ing slant line show ing the phase changing w ith x and t .It is easy to show that the phase differ ence of incident and r eflected w aves is independent of the time and the node and loo p of the wav e are fo und easily.Key words phase;phase difference;phase diagram(上接9页)THE FRAUNHOFER DIFFRACTION AT A CIRCULARDISC ILLUMINATED BY A GAUSSIAN BEAMRang Qinglan(Depart ment of P hy sics,P eking U niv ersit y,Beijing ,100871,China)Abstract The g ener al expression of the diffraction field at a cir cular aperture (or disc )illu-minated by a Gaussian beam is derived.A systematic set of data of the abov e diffraction field for so me particular co nditions w ith a near -zero number o f half-period zones is calculated.T he phe-no menon of a dark ring in the Air y disc for the diffraction field at an opaque strip (or a disc )is explained .Key words diffractio n at a cir cular disc;Gaussian beam ;Fresnel's half-period zo nes23第11期 罗治安等:用相位图分析驻波形成。

第62卷 第1期吉林大学学报(理学版)V o l .62 N o .1 2024年1月J o u r n a l o f J i l i nU n i v e r s i t y (S c i e n c eE d i t i o n )J a n 2024d o i :10.13413/j .c n k i .jd x b l x b .2022455高斯激光束在F r a u n h o fe r圆孔衍射成像中的球差夏雄平,张 凯,韦贵妹,田恺婧(桂林理工大学物理与电子信息工程学院,广西桂林541004)摘要:基于标量衍射理论,利用Z e r n i k e 多项式法构建像差函数,并将其应用到Z E MA X 中,研究高斯型激光束在透镜与圆孔距离较大时的F r a u n h o f e r 圆孔衍射成像中的球差.实验和理论模拟结果表明,透镜及圆孔和透镜距离对产生球差的影响较大,当选择优化的非球面透镜㊁较高折射率的透镜材料和小视场时,可有效降低由圆孔和透镜距离较大而产生的球差,从而有效提升衍射成像质量.关键词:F r a u n h o f e r 圆孔衍射;球差;高斯激光束;Z e r n i k e 多项式中图分类号:O 436.1 文献标志码:A 文章编号:1671-5489(2024)01-0141-06S p h e r i c a lA b e r r a t i o n s o fG a u s s i a nL a s e rB e a mi n F r a u n h o f e rC i r c u l a rA p e r t u r eD i f f r a c t i o n I m a g i n gX I A X i o n g p i n g ,Z H A N G K a i ,W E IG u i m e i ,T I A N K a i j i n g(C o l l e g e o f P h y s i c s a n dE l e c t r o n i c I n f o r m a t i o nE n g i n e e r i n g ,G u i l i nU n i v e r s i t y o f T e c h n o l o g y ,G u i l i n 541004,G u a n g x i Z h u a n g A u t o n o m o u sR e gi o n ,C h i n a )A b s t r a c t :B a s e do n s c a l a r d i f f r a c t i o n t h e o r y ,t h e a b e r r a t i o n f u n c t i o nw a s c o n s t r u c t e db y u s i n g Z e r n i k e p o l y n o m i a l m e t h o d ,a n dt h ea b e r r a t i o nf u n c t i o n w a sa p p l i e dt o Z E MA X t os t u d y t h es ph e r i c a l a b e r r a t i o n o f G a u s s i a nl a s e r b e a m i n F r a u n h o f e rc i r c u l a ra p e r t u r e d i f f r a c t i o ni m a g i n g w h e nt h e d i s t a n c eb e t w e e nl e n sa n dc i r c u l a ra p e r t u r ew a s l a r g e .T h ee x p e r i m e n t a l a n dt h e o r e t i c a l s i m u l a t i o n r e s u l t s s h o wt h a t t h e l e n s a n d t h e d i s t a n c eb e t w e e n l e n s a n dc i r c u l a r a p e r t u r eh a v e s i g n i f i c a n t e f f e c t s o n s p h e r i c a l a b e r r a t i o n .W h e n s e l e c t i n g o p t i m i z e da s p h e r i c l e n s ,l e n sm a t e r i a l sw i t hh i g h e r r e f r a c t i v e i n d e xa n d s m a l l f i e l d -o f -v i e w ,i t c a n e f f e c t i v e l y r e d u c e t h e s p h e r i c a l a b e r r a t i o n c a u s e d b y l a r g e d i s t a n c e b e t w e e n l e n s a n d c i r c u l a r a p e r t u r e ,t h e r e b y e f f e c t i v e l y i m p r o v i n g t h e d i f f r a c t i o n i m a g i n gq u a l i t y .K e yw o r d s :F r a u n h o f e r c i r c u l a r a p e r t u r e d i f f r a c t i o n ;s p h e r i c a la b e r r a t i o n ;G a u s s i a n l a s e r b e a m ;Z e r n i k e p o l y n o m i a l 收稿日期:2022-11-18.第一作者简介:夏雄平(1979 ),男,汉族,博士,教授,从事非线性光学和应用光学的研究,E -m a i l :x x p c c p @163.c o m.基金项目:国家自然科学基金(批准号:11447169)和广西自然科学基金(批准号:2018G X N S F A A 138180).光衍射成像技术广泛应用于通信㊁生物医学和材料检测等领域[1-2].由于光在衍射过程中受介质㊁元件尺寸和材料等因素影响,因此产生各种像差,其中球差是因为轴上单色同心光束经过光学系统后,不同孔径光线相交光轴不同位置,导致在成像面上形成了以高斯像点为中心的弥散斑,从而成为影响成像清晰度和质量的重要因素[3-5].光学衍射成像的理论基础为H u y g e n s -F r e s n e l 原理和K i r c h o f f 衍射积分,其成像分析可分为标量衍射和矢量衍射方法.对大口径元件一般用标量衍射法[6-8],当微光学元件的尺寸接近或小于光波长时,采用矢量衍射法[9].像差研究方法包括几何方法[10]㊁计算机模拟方法[11]和Z e r n i k e 函数法[12-14]等.由于Z e r n i k e 多项式构建像差函数和光学检测中观测到的像差多项式形式一致,因此Z e r n i k e 多项式广泛应用于分析像差研究中:W a n g 等[15]利用Z e r n i k e 多项式法提出了通过优化成像位置和增加相位补偿器,可有效控制圆孔衍射波前畸变;Z h a n g 等[16]基于Z e r n i k e 多项式拟合的相位畸变方法,提出了圆孔衍射波前畸变模型;H s i e h 等[17]利用优化的Z e r n i k e 函数,提出了一种对像差分析和模式识别更有效的算法;N e m e s -C z o p f 等[18]用参数建模和标量衍射在Z E MA X 软件中模拟浮雕型衍射透镜.对比一般F r a u n h o f e r 圆孔衍射中透镜紧贴圆孔的情形,本文以广义H u y g e n s -F r e s n e l 衍射理论为基础,采用标量衍射理论,将通过Z e r n i k e 多项式构建的像差函数应用到Z E MA X 软件中,并根据实验结果和利用Z e r n i k e 多项式法分析实验出现的像差所对应的阶数,实现激光衍射光斑通过Z 8阶Z e r n i k e 形变的像差透镜,研究高斯激光束在圆孔与透镜距离较大时的F r a u n h o f e r 圆孔衍射成像中的球差,并在此基础上提出有效控制球差的方法.1 圆孔衍射成像机制在圆孔衍射中,从H u y g e n s -F r e s n e l 原理出发,若点光源距离衍射屏足够远,则其积分公式可写为E (p )=A i λz ∬E (x 0,y 0,0)e x p {i k r }d σ,(1)其中r =(x -x 0)2+(y -y 0)2+z 2,E (x 0,y 0,0)为z =0处的初始波函数,其表达式中可涵盖多种系数成分,可通过迭代法程序的近似计算得到积分结果.若满足z ≫(x -x 0)2+(y -y 0)2,则E (p )满足F r e s n e l 傍轴近似,若继续满足远场条件z ≫k (x 20+y 20)/2,则可得F r a u n h o f e r 衍射近似表达式E (x ,y ,z )≃A i λz e x p i k x 2+y 22æèçöø÷{}z ∬E (x 0,y 0,0)e x p -i k x x 0+y y 0æèçöø÷{}z d x 0d y 0,(2)当采用极坐标时,方程(2)可转换为E (r ,φ)≃e x p {i k z }e x p {i (k r 2/(2z ))}i λz ʏ2π0ʏE (ρ,θ)e x p {-i (k r ρ/z )c o s (φ-θ)}ρd ρd θ,(3) 利用B e s s e l 函数的积分式和递推性质,可得x 处的光强分布为I 0(x )=12πʏ2π0e x p {-i x c o s φ}d φ,(4)d [x J 1(x )]d x =x J 0(x ),(5)光强分布可进一步简化为I =I 02J 1(z )éëêêùûúúz 2,(6)其中I 0=πc a 22是衍射屏中心光强,J 0和J 1分别为零阶B e s s e l 函数和一阶B e s s e l 函数.根据圆孔衍射的定义可知,在传播距离z =0处,光强最强,当z 满足J 1(z )=0时,光强有极小值0,这些z 值取决于衍射暗环的位置.相邻两个暗环之间出现一个明亮的条纹,同理相邻条纹之间也会有一个暗环.在方程(3)中引入Z e r n i k e 函数,利用迭代方法可得包含Z e r n i k e 函数的衍射积分.其中初始波函数E (ρ,θ)若为高斯型激光束,在此取基模T E M 00高斯光束,则其表达式为E (ρ,θ)=C 00e x p -r 2r2{}m a x (c o s k +i s i n k )Z l N (ρ,θ),(7)其中C 00表示基模光束的系数,指数部分表示光束呈高斯型分布,Z l N (ρ,θ)表示Z e r n i k e 多项式函数的表达式,N 为阶数.基于Z e r n i k e 多项式函数本身的对称特性,其表达式在单位圆上满足正交规律ʏ10ʏ2π0Z l N (ρ,θ)ρd ρd θ=πn +1δn n .(8) Z e r n i k e 标准矢高表面类型可使用多达231个Z e r n i k e 标准多项式定义表面矢量高,其标准矢高241 吉林大学学报(理学版) 第62卷表面描述的是表面变形. E x t r a p o l a t e 用来指定在计算时使用的最大Z e r n i k e 多项式项表面矢量,该数字用来加速射线追踪计算,可忽略超过该数字的项.表面矢高的形式为h =c r 21+1-(1+k )c 2r2+ð8i =1αi r 2i +ðMi =1A i Z i (ρ,θ),(9)其中M 为系列中Z e r n i k e 系数的数量,A i 为Z e r n i k e 标准多项式上i t h 的系数,r 为透镜单位的径向射线坐标,ρ为归一化的径向射线坐标,φ为角射线坐标.2 实验与仿真模拟结果在F r a u n h o f e r 圆孔衍射中,采用波长为641n m 的激光作为点光源,将点光源通过由双透镜构成的组合透镜L 1对基模高斯光束进行准直,准直后的高斯光束通过圆孔和圆孔后方透镜L 2后,在光屏上产生F r a u n h o f e r 圆孔衍射图像.其中圆孔直径d =0.3mm ,透镜L 2焦距f =20mm ,透镜L 2与圆孔间距分别为C 1=100mm 和C 2=400mm ,圆孔与衍射光屏距离为800mm.在实验开始前,先理论模拟透镜L 2紧贴圆孔时无像差影响下的结果,如图1(A )所示,再根据实验参量,得到透镜L 2与圆孔距离较大时的实验结果,分别如图1(B )和(C )所示.图1 无像差影响下的理论模拟结果(A )和F r a u n h o f e r 圆孔衍射实验结果(B ),(C )F i g .1 T h e o r e t i c a l s i m u l a t i o n r e s u l tw i t h o u t a b e r r a t i o n i n f l u e n c e (A )a n dF r a u n h o f e r c i r c u l a r a p e r t u r e d i f f r a c t i o n e x p e r i m e n t a l r e s u l t s (B ),(C )由图1(A )可见,理论模拟的衍射图像呈圆形,条纹窄而清晰,且分布范围较大.由图1(B )和(C )可见,当透镜L 2与圆孔距离较大时,除中心A i r y 斑和少数几个衍射环呈较好的圆形外,其较高级数的衍射环连续性变差,且在其垂直于轴向方向形成了较明显的弥散斑和垂轴球差,其原因可能是透镜形状㊁折射率和焦距以及圆孔和透镜的距离等因素导致产生球差.图1(B )的衍射条纹分布较均匀且清晰度较高,随着圆孔和透镜距离的增大,图1(C )中条纹分布的均匀度和清晰度均明显降低,因此,透镜和衍射孔之间的距离对圆孔衍射影响较大.基于实验结果,根据在极坐标形式下的F r a u n h o f e r 衍射公式中引入Z e r n i k e 多项式所构建的圆孔衍射积分函数,用Z E MA X 软件仿真模拟对圆孔衍射中衍射成像的球差进行分析.其中凸透镜曲率半径r =10.336,镜片厚度2mm ,镜片材质为常用玻璃材料B K 7,采用中心视场(0,0.01,0.02)观测,其他参量与实验一致.在模拟过程中,通过引入Z e r n i k e 表面形变,根据实验出现的垂轴球差现象,对341 第1期 夏雄平,等:高斯激光束在F r a u n h o f e r 圆孔衍射成像中的球差441吉林大学学报(理学版)第62卷应在Z e r n i k e多项式法研究像差在Z8时会产生球差与离焦现象,因此在Z E MA X软件仿真模拟中,采用的Z e r n i k e多项式为Z8阶,得到光斑强度晕染图和视场点列图如图2所示.由图2(A)和(B)可见,衍射图像呈椭圆状,产生了较明显的球差现象,其原因可能与透镜㊁激光或圆孔本身有关.随着透镜与圆孔距离的增大,其球差变得更明显,表明透镜和圆孔距离对球差有直接影响.由图2(C)和(D)可见:在增大视场条件下,球差现象变得更明显;在相同视场条件下,当增大透镜和圆孔距离时,其球差也会变得更明显.因此为有效调控球差,需采取小角度视场和适当的透镜和圆孔间距.图2光斑强度晕染图(A),(B)和视场点列图(C),(D)F i g.2S p o t i n t e n s i t y b l o o m i n g c h a r t(A),(B)a n d s p o t d i a g r a m(C),(D)针对实验和仿真模拟在衍射成像过程产生的球差,根据Z E MA X软件特点,通过添加评价函数优化镜片,利用优化圆锥系数将球面透镜转换成非球面透镜,优化后的曲率半径为18.836mm,此时有效焦距降低至19.9997mm,圆锥系数为25.696,透镜采用较高折射率的透镜材料(S F59)和小视场,从而从整体上有效调控球差,得到的仿真结果如图3所示.对比系统未优化的结果(图2),由图3可见,在小视场条件下,当采用优化的非球面透镜和较高折射率材料的透镜时,一方面其衍射图像从椭圆变成圆形,其中的球差现象几乎消失,其衍射圆环的分布与理想条件下的理论模拟结果相符,图像的清晰度和成像质量明显提升,此时透镜和圆孔距离对成像质量的影响变弱;另一方面,当C=100mm和C=400mm时,相比实验(图1)和系统未优化的结果(图2),光斑分布变得更均匀,光斑大小和性质受透镜和圆孔距离的影响减弱,进而提升了成像质量.为分析图像的解像力,得到优化前后传递函数(MT F)随空间频率的变化关系,空间频率的单位为线对每毫米(l p/mm),结果如图4所示,其中a和d为优化前的MT F曲线,b和c为优化后的MT F 曲线,虚线和实线分别表示子午和弧矢面的不同成像质量,由于衍射极限的差异,因此曲线b略低于曲线a,但MT F曲线均接近A i r y斑.由边缘视场MT F曲线c和d可见,优化后的MT F值明显优于未优化时的结果,其解像力更强,有利于降低衍射过程中球差和慧差的影响,其成像质量更好.图3 光斑强度晕染图(A ),(B )和光斑强度局部放大线性图(C ),(D )F i g .3 S p o t i n t e n s i t y b l o o m i n g c h a r t (A ),(B )a n d l o c a lm a g n i f i c a t i o n l i n e a r g r a p ho f s p o t i n t e n s i t y (C ),(D )图4 M T F 定量对比曲线F i g .4 M T F q u a n t i t a t i v e c o m p a r i s o n c u r v e s 综上,本文将Z e r n i k e 多项式法构建的像差函数应用到Z E MA X 中,并结合圆孔衍射实验结果,对高斯型激光束在透镜和圆孔距离较大时的F r a u n h o f e r 圆孔衍射成像中的球差进行了研究.首先,通过实验分析了高斯型激光束在透镜与圆孔距离较大时的F r a u n h o f e r 圆孔衍射成像特点,对衍射成像中出现的球差进行了分析;其次,利用Z E MA X 仿真模拟对衍射成像中的球差进行了研究.理论模拟和实验结果表明:透镜及透镜和圆孔距离对产生球差影响较大,当选择优化的非球面透镜㊁较高折射率的透镜材料和小视场时,可有效降低圆孔和透镜距离较大时产生的球差,从而有效提升衍射成像质量,该研究结果可为实际衍射光学系统的透镜设计和制造提供理论指导.参考文献[1] L E EK ,K I M K ,K I M G ,e t a l .T i m e -M u l t i p l e x e dS t r u c t u r e d I l l u m i n a t i o nU s i n g aD M Df o rO p t i c a lD i f f r a c t i o n T o m o g r a p h y [J ].O p t i c sL e t t e r s ,2017,42(5):999-1002.[2] P H E L A N CF ,O DWY E RDP ,R A K O V I C H YP ,e t a l .C o n i c a l D i f f r a c t i o n a n dB e s s e l B e a mF o r m a t i o nw i t h aH i g hO p t i c a lQ u a l i t y B i a x i a l C r y s t a l [J ].O p t i c sE x p r e s s ,2009,17(15):12891-12899.[3] F E N GP ,T A N GF ,WA N G XZ ,e t a l .D u a l -F i b e rP o i n tD i f f r a c t i o nI n t e r f e r o m e t e r t o M e a s u r e t h e W a v e f r o n t A b e r r a t i o no f a n I m a g i n g S y s t e m [J ].A p p l i e dO p t i c s ,2020,59(10):3093-3096.[4] Z HA O L ,D O NG LJ ,Y U XF ,e t a l .A c t i v eL e n s f o rT h e r m a lA b e r r a t i o nC o m p e n s a t i o n i nL i t h o g r a p h y Le n s [J ].A p p l i e dO p t i c s ,2018,57(29):8654-8663.[5] A N I T A G T ,M I L T O N A.F o c u s i n g o fT i g h t l y F o c u s e dA z i m u t h a l l y P o l a r i z e dD o u b l eR i n g B e a m b y aLe n s i n t h eP r e s e n c e o fC o m aA b e r r a t i o n [J ].O p t i k ,2019,192:162924-1-162924-5.[6] S U G I S A K AJ ,Y A S U IT ,H I R A Y AMA K.P r of i l eR e c o n s t r u c t i o no f aL o c a lD e f e c t i naG r o o v eS t r u c t u r ea n d 541 第1期 夏雄平,等:高斯激光束在F r a u n h o f e r 圆孔衍射成像中的球差641吉林大学学报(理学版)第62卷t h eT h e o r e t i c a l L i m i t u n d e r t h eV e c t o rD i f f r a c t i o nT h e o r y[J].O p t i c sE x p r e s s,2020,28(21):30908-30927.[7] HA NP,HWA N G H E,Y A N G G H.F r a u n h o f e ra n dF r e s n e lD i f f r a c t i o nC h a r a c t e r i s t i c so f aT i m eD e p e n d e n tG a u s s i a n-S h a p e dP u l s e dB e a mf r o ma n I n f i n i t eE d g e[J].C h i n e s e J o u r n a l o fP h y s i c s,2003,41(4):372-382.[8] B O F F IP,O S MO N DJ,P I C C I N I N D,e t a l.D i f f r a c t i o no fO p t i c a lC o mm u n i c a t i o nG a u s s i a nB e a m sb y V o l u m eG r a t i n g s:C o m p a r i s o no f S i m u l a t i o n s a n dE x p e r i m e n t a lR e s u l t s[J].A p p l i e dO p t i c s,2004,43(19):3854-3865.[9] Z HA N GF,WA N G C,Y I N K,e ta l.U n d e r w a t e rG i a n tE n h a n c e m e n to fB r o a d b a n d D i f f r a c t i o n E f f i c i e n c y o fS u r f a c eD i f f r a c t i o nG r a t i n g sF a b r i c a t e db y F e m t o s e c o n dL a s e r[J].J o u r n a l o fA p p l i e dP h y s i c s,2017,121(24): 243102-1-243102-6.[10] MA L A C A R A-D O B L A D O D,MA L A C A R A-H E R N A N D E Z Z,G OM E Z-V I E Y R A A.P r i m a r y W a v e f r o n tA b e r r a t i o n sC a l c u l a t i o nf r o m a D e f o c u s e dI m a g eo ra H a r t m a n n g r a m[J].A p p l i e d O p t i c s,2010,49(12):2302-2308.[11] S U W C,Z HO U S K,L I N B S,e ta l.S i m p l i f i e d A b e r r a t i o n A n a l y s i s M e t h o do f H o l o g r a p h i c W a v e g u i d eC o m b i n e r[J].P h o t o n i c s,2020,7(3):71-1-71-12.[12] L I U D,WU SB,Y A N G W,e t a l.E f f e c t so fM a s k-A l i g n m e n tE r r o ro nP o i n tS p r e a dF u n c t i o nf o r M u l t i-l e v e lF r e s n e lD i f f r a c t i v eL e n s e s[J].C h i n e s eO p t i c sL e t t e r s,2018,16(9):090501-1-090501-6.[13] R O S E NJ,HA IN,R A IM R.R e c e n tP r o g r e s s i nD i g i t a lH o l o g r a p h y w i t hD y n a m i cD i f f r a c t i v eP h a s eA p e r t u r e s[J].A p p l i e dO p t i c s,2022,61(5):B171-B180.[14] Y U H H,C HA N G J,L I U X,e ta l.N o v e lA s y mm e t r i cC r y p t o s y s t e m B a s e do n D i s t o r t e d W a v e f r o n tB e a mI l l u m i n a t i o na n dD o u b l e-R a n d o m P h a s eE n c o d i n g[J].O p t i c sE x p r e s s,2017,25(8):8860-8871.[15] WA N G QZ,X I AXP.A b n o r m a l D i s t o r t i o n a n dC o n t r o l o f aG a u s s i a nB e a mi nC i r c u l a rA p e r t u r eD i f f r a c t i o n[J].A p p l i e dO p t i c s,2021,60(32):10035-10041.[16] Z HA N GSZ,L IXB,J E O N G H.A n a l y t i c a l D i f f r a c t i o nC o r r e c t i o n s f o rC i r c u l a rF o c u s e dT r a n s d u c e r sE x p r e s s e dU s i n g t h eM u l t i-G a u s s i a nB e a m M o d e l[J].A c t aA c u s t i c aU n i t e dw i t hA c u s t i c a,2017,103(5):717-720. [17] H S I E H Y H,Y U YT,L A IY H,e t a l.I n t e g r a l-B a s e dP a r a l l e lA l g o r i t h mf o r t h eF a s tG e n e r a t i o n o f t h e Z e r n i k eP o l y n o m i a l s[J].O p t i c sE x p r e s s,2020,28(2):936-947.[18] N E M E S-C Z O P FA,B E R C SÉN Y ID,E R D E IG.S i m u l a t i o no fR e l i e f-T y p eD i f f r a c t i v eL e n s e s i nZ E MA X U s i n gP a r a m e t r i cM o d e l l i n g a n dS c a l a rD i f f r a c t i o n[J].A p p l i e dO p t i c s,2019,58(32):8931-8942.(责任编辑:王健)。

3类高斯光束的圆孔衍射特性韩振海【摘要】利用标量衍射理论,将空心高斯光束、贝塞尔高斯光束、平顶高斯光束3类高斯光束的圆孔衍射场进行傅里叶变换,并运用D-FFT算法对其圆孔衍射特性进行了数值计算,得到了衍射场中轴向和径向的光强分布特点,分析了光学参量对衍射结果的影响.分析结果表明:衍射特性与衍射距离、光束的阶数、圆孔束腰半径比等因素有关.【期刊名称】《物理实验》【年(卷),期】2016(036)006【总页数】7页(P12-18)【关键词】空心高斯光束;贝塞尔高斯光束;平顶高斯光束;圆形光阑;衍射;傅里叶变换【作者】韩振海【作者单位】河西学院物理与机电工程学院,甘肃张掖734000【正文语种】中文【中图分类】O436.1激光在具体应用时，对激光模式、束型、强度分布、光斑大小等都有严格地要求. 近年来对一些特殊类型高质量空心光束的研究已成为光学应用领域研究的热点，其研究成果在激光光学、二元光学、全息光学、原子冷却、光信息处理、微粒波导、生物医学等领域都有了广泛应用. 拉盖尔-高斯光束是一种轴向强度为零的暗中空光束，而高阶拉盖尔-高斯光束具有携带轨道角动量和环状强度分布的特点，该类光束沿轴向传播有螺旋的相位结构，能携带更多的信息量，在轨道角动量纠缠态的产生、量子加密、引力波探测、粒子操控、光镊、光通信等方面具有不可替代的优势. 高阶贝塞尔光束是一种具有无衍射特性的空心光束，具有相位奇点中心光强为零的特点，而周围存在高强度的光分布，这种空心光阱比实心光阱对微粒具有更好的捕获能力. 面包圈空心光束是一种特殊的类似于高阶拉盖尔-高斯光束的空心光束，这种空心光束是发散的，且具有自旋和轨道角动量，可用作光镊和实现微观粒子的囚禁. LP01模输出空心光束是一种发散光束，它在近场的分布类似于高斯分布，在远场的分布是一个空心环状分布，该光束具有轨道角动量，可用于微观粒子的囚禁和激光加工等. 双高斯分布的空心光束是一种径向强度呈高斯变化的空心光束，具有轨道角动量和较强的强度梯度，可用于中性原子的激光冷却及其冷原子束的激光准直等. 聚焦空心光束是将空心光束或高斯光束先经过一个特殊的π相位板后再经过透镜聚焦而成，聚焦光束无论是在焦点附近还是远离焦点都是空心的，可以用作原子(分子)透镜来聚焦原子束(分子束)，也可实现中性原子的冷却. 空心高斯光束、平顶高斯光束具有不同于一般高斯光束的物理性质[1-2]，而贝塞尔高斯光束则在一定条件下呈现“无衍射”等特性[3]，对这类光束的研究引起了人们极大地关注[4-9]，了解它们通过有限光阑的传输和衍射特性就显得非常重要. 本文利用标量衍射理论，将空心高斯光束、贝塞尔高斯光束、平顶高斯光束等3类高斯光束的圆孔衍射场表示成傅里叶变换的形式，并运用D-FFT算法对其圆孔衍射特性进行了数值计算，得到了衍射场中轴向和径向的光强分布特点，分析了光学参量对衍射结果的影响.圆孔的透过率可用圆域函数表示为式中R0表示圆孔半径. 为简单计算，将圆孔面置于以下3类高斯光束的束腰处(z=0).1.1 3类高斯光束的模型1)空心高斯光束空心高斯光束在z=0处的光场分布为式中:A0=E0(0,0)，ω0表示束腰半径，n表示空心高斯光束的阶数. 图1给出了空心高斯光束在束腰处的径向光强分布. 空心高斯光束在圆孔后表面上的光场分布为.2)贝塞尔高斯光束贝塞尔高斯光束在z=0处的光场分布为式中：J0 (αr0)为第一类零阶贝塞尔函数，α表示横向波数. 图2给出了空心高斯光束在束腰处的径向光强分布. 贝塞尔高斯光束在圆孔后表面上的光场分布为.3)平顶高斯光束平顶高斯光束在z=0处的光场分布为E0 (r0,0)=m=0,1,2,…,式中M表示平顶高斯光束的阶数(M=0,1,2,…). 图3给出了平顶高斯光束在束腰处的径向光强分布. 平顶高斯光束在圆孔后表面上的复振幅分布为1.2 3类高斯光束通过圆孔的衍射场计算对于轴对称近轴光学系统，其传输矩阵为，而自由空间中的传输变换矩阵则为. 根据圆孔后表面上的光波场U0(r0,0)，可由Collins公式计算衍射空间的光波场U(r,z)，即.式中z表示观察面和入射面之间的距离.将(8)式积分号内关于x和y的复相位因子作配方处理并作变量代换xa=Ax0，ya=Ay0，可得到利用(9)式，可将(8)式写为卷积形式,式中*表示卷积运算. 以fx 和fy表示频率域坐标，可得到,式中F{ }表示傅里叶变换. 利用卷积定理可将(10)式表示为U(x,y,z)= exp (jkz)·,式中F-1 { }表示傅里叶逆变换. 这样利用2次傅里叶变换并借助于D-FFT算法[10]，就可求出高斯光束通过圆孔后在空间传输的衍射场分布.数值计算[11-12]中衍射面大小为10 mm×10 mm，衍射面上抽样点数取512×512，激光波长为632.8 nm，束腰半径ω0=1 mm.2.1 空心高斯光束圆孔衍射特性的计算位于衍射面中央的圆孔半径R0=2 mm. 图4是在空心高斯光束的阶数n=3，其他参量不变时，不同衍射距离处轴上的光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，当传输距离较小(z<500 mm)时，轴上光强为零；随着衍射距离的增大，轴上光强逐渐增大，在z≈4 000 mm处轴上光强达到极大值；进一步增大衍射距离，轴上光强随之减小，但在该范围内有一定的起伏变化. 图5是在空心高斯光束的阶数n=3，其他参量不变时，不同衍射距离处接收面上的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，近距离范围内(z<500 mm)接收面上的光强与空心高斯光束束腰处的分布相似，中心为暗斑；随着衍射距离的增大，中心逐渐有光能量聚集，在中心亮斑之外有暗、亮环交替出现，衍射效应明显，且亮环内的光强随半径也成高斯型分布；在z≈4 000 mm处中心亮斑的光强达到极大值；之后增大衍射距离，中心亮斑的强度下降，半径增大，衍射调制作用有所减弱.图6是在其他参量不变时，不同阶数n的空心高斯光束在z=500 mm处的接收面上产生的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，阶数n较小时，中心暗斑的半径、亮环的半径均较小，n较大时，中心暗斑的半径、亮环的半径也较大，空心性越好；但亮环的宽度和光强则基本一致，没有随阶数发生明显的变化. 图7是在空心高斯光束的阶数n=5，改变圆孔大小(在束腰不变的条件下，亦即改变圆孔与束腰半径比)，而其他参量不变时，空心高斯光束在传输距离z=1 000 mm处的接收面上产生的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，圆孔与束腰半径比对中心亮斑的大小没有明显影响(中心亮斑的宽度基本相同)；但半径比越大，中心亮斑的强度就越小，中心亮斑外围的亮环数也减少，衍射调制作用减弱.2.2 贝塞尔高斯光束圆孔衍射特性的计算位于衍射面中央的圆孔半径R0=2 mm. 图8是在贝塞尔高斯光束的径向波数α=5，其他参量不变时，不同衍射距离处轴上的光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，当传输距离较小(z<400 mm)时，轴上光强值很大；当增大衍射距离(z>400 mm)时，轴上光强急剧减小，并在该范围内没有出现较大的起伏变化. 图9是在横向波数α=5，其他参量不变时，不同衍射距离处接收面上的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，近距离范围内(z<100 mm)接收面上的中心亮斑之外有暗、亮环交替出现，呈现出一定的衍射效应；但当衍射距离增大后，中心亮斑光强分布变得比近距离时平滑，同时衍射效应非常微弱.图10是在其他参量不变时，不同横向波数α的贝塞尔高斯光束在z=300 mm处的接收面上产生的光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，横向波数α对中心亮斑的宽度没有明显影响，只是α较大时，中心亮斑的光强有所减小. 图11是在横向波数α=5，改变圆孔大小(改变圆孔与束腰半径比)，而其他参量不变时，贝塞尔高斯光束在z=300 mm处的接收面上产生的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，圆孔与束腰半径比对中心亮斑的大小没有明显影响(中心亮斑的宽度基本相同)；但半径比越大，中心亮斑的强度就越小.2.3 平顶高斯光束圆孔衍射特性的计算位于衍射面中央的圆孔半径依然取R0=2 mm. 图12是在平顶高斯光束的阶数M=3，其他参量不变时，不同衍射距离处轴上的光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，随着衍射距离从零开始增大，轴上光强也从零开始逐渐增大，在z≈1 800 mm处轴上光强达到极大值；进一步增大衍射距离，轴上光强随之减小，但在该范围内没有像前述空心高斯光束那样出现较明显的光强起伏变化. 图13是在平顶高斯光束的阶数M=3，其他参量不变时，不同衍射距离处接收面上的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，近距离范围内接收面上的光强与平顶高斯光束束腰处的分布相似，中心为暗斑；随着衍射距离的增大，中心逐渐有光能量聚集，且在中心亮斑之外有较微弱的亮、暗环交替出现；之后增大衍射距离，中心亮斑的强度下降，半径增大. 值得注意的是，平顶高斯光束在整个衍射距离范围内并没有表现出像空心高斯光束那样明显的衍射调制效应.图14是在其他参量不变时，不同阶数M的空心高斯光束在z=1 000 mm处的接收面上产生的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，阶数M对中心亮斑的半径和宽度没有产生明显的影响，但是阶数越大，旁瓣数越少，光强的径向变化越加平滑，衍射效应越不明显. 图15是在平顶高斯光束的阶数M=5，改变圆孔大小(改变圆孔与束腰半径比)，而其他参量不变时，平顶高斯光束在z=1 000 mm处的接收面上产生的径向光强分布. 从计算结果可以看到，在选取以上实验参量的条件下，圆孔与束腰半径比对中心亮斑的大小没有明显影响(中心亮斑的宽度基本相同)；当R0/ω0=0.8时，中心亮斑的强度较大，外围有强度的交替性变化，呈现出一定的衍射效应；当R0/ω0≥1.1时，中心亮斑的强度较小，外围的强度交替变化减弱，衍射效应不明显.对比以上计算结果，可以看出：1)在轴上的纵向光强分布中，空心高斯光束和平顶高斯光束表现出基本相同的变化规律(在特定距离处光强达到最大，而在较近距离和较远距离处光强则较小)，只是在远场前者的强度起伏更强烈；而贝塞尔高斯光束仅当传输距离很小时，轴上光强值很大，而当增大衍射距离时，轴上光强便急剧衰减.2)在衍射场的径向光强分布中，空心高斯光束和平顶高斯光束中心亮斑都随着衍射距离的增大而增大，能量逐渐向径向延展，前者在较近距离处还表现出明显的衍射效应，后者则不甚明显；而贝塞尔高斯光束的衍射光能量则高度聚集在中央轴线处.3)阶数影响空心高斯光束中心暗斑的半径、亮环的的半径，但对亮环的宽度和光强没有产生明显影响；横向波数只对贝塞尔高斯光束中心亮斑的光强有所影响，而对其宽度则没有明显影响；阶数对平顶高斯光束中心亮斑的旁瓣数以及光强变化的平滑度产生影响.4)圆孔与束腰半径比对空心高斯光束中心亮斑的强度及其旁瓣数、衍射调制结果都有明显的影响；对贝塞尔高斯光束只影响中心亮斑的强度；对平顶高斯光束的衍射调制结果有一定的影响.3类高斯光束的圆孔衍射具有各自不同的特性. 在空心高斯光束的圆孔衍射中，纵向和径向的光强与衍射距离密切相关，且阶数和圆孔束腰半径比对衍射结果产生明显影响，阶数越高，衍射效应越不明显；贝塞尔高斯光束的横向波数和圆孔束腰半径比对衍射结果无明显影响，衍射效应微弱，光能量高度聚集在中央轴线处，呈现出“聚焦”效应；阶数和圆孔束腰半径比对平顶高斯光束衍射结果产生一定的影响.这些特点对于进一步研究各类高斯光束有一定的理论和实践价值，也有利于高斯光束在光学工程中的实际应用.【相关文献】[1] 张蕾,蔡阳健,陆璇辉. 一种新空心光束的理论及实验研究[J]. 物理学报, 2004,53(6):1777-1781.[2] Bagini V, Borghi R, Gori F, et al. Propagation of axially symmetric flattened Gaussian beams [J]. J. Opt. Soc. Am. A, 1996,13(7):1385-1394.[3] Liu Y X, Ge W G, Lv B D. Diffraction characteristics of Bessel-Gauss beams limited by apertures [J]. Opto-Electronic Engineering, 2005,32(12):17-20.[4] Tang B, Jiang S B, Jiang C, et al. Propagation properties of hollow sinh-Gaussian beams through Fractional Fourier transform optical systems[J]. Optics & Laser Technology, 2012,20(9):9682-9691.[5] Sun Q G, Zhou K Y, Fang G Y, et al. Hollow sinh-Gaussian beams and their paraxial properties [J]. Optics Express, 2014,59(4):116-122.[6] 黄慧琴，赵承良，陆璇辉. 空心光束的研究进展[J]. 激光与红外，2007，37(4)：300-303.[7] Wu G H, Guo H, Deng D M. Paraxial propagation of partially coherent flat-topped beam[J]. Opt. Commun., 2006,260(2):687-690.[8] F Gori, M Santarsiero. Twisted Gaussian schell-model beams as series of partially coherent modified Bessel-Gauss beams [J]. Optics Letters, 2015,40(7):1587-1590.[9] Zhang Z M, Pu J X, Wang X Q. Focusing of partially coherent Bessel-Gaussian beams through a high-numerical-aperture objective [J]. Optics Letters, 2008,33(1):49-51.[10] 李俊昌. 衍射计算及数字全息[M]. 北京：科学出版社，2014.[11] Voelz D G. Computational Fourier optics [M]. Washington： SPIE Press， 2010.[12] 国承山，李传涛，洪正平，等. 光衍射数值模拟中不同抽样方法的适用性分析[J]. 光学学报，2008，28(3)：442-446.。