一般锐角的三角函数值

初中正弦余弦正切公式“初中数学必背三角函数公式、三角函数值”主要包括正弦、余弦、正切函数的定义式和关系式，特殊锐角的正弦、余弦、正切值。

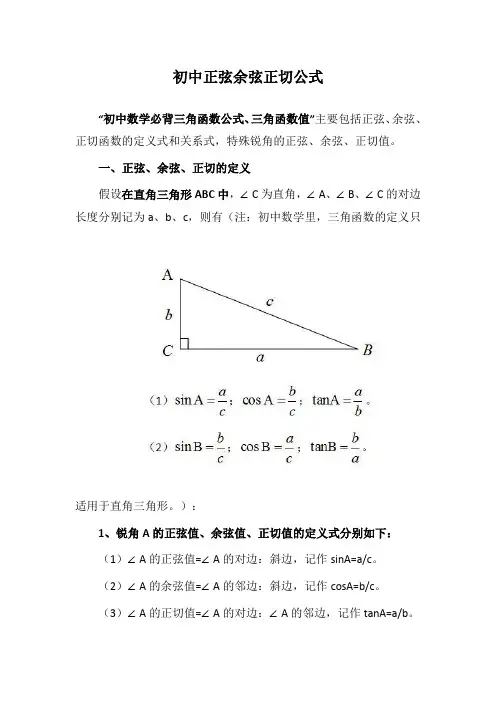
一、正弦、余弦、正切的定义假设在直角三角形ABC中，∠C为直角，∠A、∠B、∠C的对边长度分别记为a、b、c，则有（注：初中数学里，三角函数的定义只适用于直角三角形。

）：1、锐角A的正弦值、余弦值、正切值的定义式分别如下：（1）∠A的正弦值=∠A的对边：斜边，记作sinA=a/c。

（2）∠A的余弦值=∠A的邻边：斜边，记作cosA=b/c。

（3）∠A的正切值=∠A的对边：∠A的邻边，记作tanA=a/b。

2、锐角B的正弦值、余弦值、正切值的定义式分别如下：（1）∠B的正弦值=∠B的对边：斜边，记作sinB=b/c。

（2）∠B的余弦值=∠B的邻边：斜边，记作cosB=a/c。

（3）∠B的正切值=∠B的对边：∠B的邻边，记作tanB=b/a。

【注】正弦=“对比斜”、余弦=“邻比斜”、正切=“对比邻”。

3、互余的两个角间的正弦、余弦、正切值关系假设在直角三角形ABC中，∠C为直角，则∠A与∠B互余。

通过∠A和∠B的正弦、余弦、正切值的定义式的对比，我们不难发现：∠A的正弦值与∠B的余弦值相等，∠A的余弦值与∠B的正弦值相等，∠A的正切值与∠B的正切值互为倒数。

所以，当∠A与∠B互余时我们有以下3个同时成立的等式关系：（1）sinA=cosB；（2）sinB=cosA；（3）tanA·tanB=1。

二、同角的正弦值、余弦值、正切值间的关系式1、商数关系：tanA=sinA/cosA；tanB=sinB/cosB.2、平方关系：同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1，即(sinA)^2+(cosA)^2=1；(sinB)^2+(cosB)^2=1.3、倒数关系：tanA·cotA=1；tanB·cotB=1.【注】“cotA”称为为∠A的余切，它等于∠A的邻边比上∠A的对边。

锐角的三角函数值（4）——一般锐角的三角函数值导学目标：会使用计算器求锐角三角函数值，会使用计算器根据锐角三角函数值求对应的锐角。

一自主预习：1.在利用计算器求一个锐角的三角函数值时,应先使计算器设置在”“状态.标志是屏幕上显示 .2.sin-1,cos-1,tan-1键是表示由求锐角度数的功能键3.求sin400的值的按键顺序是什么？4.求值(精确到0.0001)⑴cos34035/⑵tan66015/17//二．合作探究：探究点1：求一个锐角的三角函数值。

我们知道sin300=,那么sin3002/是多少呢？说明：⑴用计算器求一个角的三角函数值时，首先要把计算器设置在“角度”状态下，也就是在计算器的显示屏上出现“DEG”的字样。

⑵在角度单位状态为度的情况下，先输入数据，再按sin,cos,tan键可以直接求出一个角的正弦，余弦，正切值了例1：用计算器求下列各三角函数的值（精确到0.001）⑴sin240⑵tan63027/ ⑶cos18059/27//例2.用计算器求：①sin100,sin200,sin300,……sin900的值.②cos100,cos200,cos300,……,cos900的值.③tan100,tan200,tan300,……,tan900的值.⑵根据所求结果总结：①随角度变化函数值的变化规律。

②同角的正余弦函数值间的关系⑵比较大小：①sin72032/ 620 ; ②cosa cosβ (a<β,a,β为锐角)⑶sin12012/ cos78030探究点二：已知三角函数值求锐角。

例.根据下列条件求∠A 的度数（用度，分，秒表示）⑴cosA=o.6753 ⑵tanA=87.54 ⑶sinA=0.4553说明：计算器中sin-1,cos-1,tan-1，这些键的功能是由正弦值，余弦值，正切值求锐角的度数。

在角度状态为“度“的情况下，求锐角时，先输入数据，再按2ndF键，再按sin-1,cos-1,tan-1键，即可得到相应的角度。

锐角三角形必背知识点1 定义直角三角形中角A的正弦（sin）,余弦（cos）和正切（tan）叫做角A的三角函数。

正弦（sin）等于对边比斜边；sinA=a/c余弦（cos）等于邻边比斜边；cosA=b/c正切（tan）等于对边比邻边；tanA=a/b锐角三角函数值的定义方法是在直角三角形中定义的，所以求锐角的三角函数值，要通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。

2 特殊角的三角函数值角度30°45°60°正弦(sin) 1/2 √2/2 √3/2余弦(cos) √3/2 √2/2 1/2正切(tan) √3/3 1 √3（注θ是锐角：0<sinθ<1 0<cosθ<1 tanθ>0）3锐角三角函数值的符号及其变化规律1）锐角三角函数值都是正值。

2）当角度在0°~90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）；余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小）；4同角三角函数基本关系式a a a tan cos sin ⋅=5互为余角的三角函数间的关系a a cos )90sin(=-a a sin )90cos(=-6 解直角三角形的基础知识在Rt ABC ∆中， 90=∠C ，A ∠，B ∠，C ∠所对的边分别为a ，b ，c（1） 三边之间的关系：222c b a =+（2） 锐角之间的关系：A ∠+B ∠=C ∠= 90（3） 边角之间的关系：c a A =sin ；c b A =cos ；ba A =tan ； c a B =cos ；c b B =sin ；ab B =tan （4） 面积公式：ch ab S 2121==∆（h 为斜边上的高） 7 解直角三角形的基本类型及其解法如下表：解直角三角形的思路可概括为“有斜（斜边）用弦（正弦、余弦），无斜用切（正切），宁乘勿除，取原避中”。

锐角三角函数。

锐角三角函数是数学中的一个重要概念，它在解决三角函数问题时起着关键作用。

锐角指的是小于90度的角，锐角三角函数包括正弦、余弦和正切三种函数，它们分别表示了锐角三角形中的比例关系。

下面我们将逐一介绍这三种函数的定义和性质。

1. 正弦函数（sine function）正弦函数是锐角三角函数中最常见的一种函数，它表示了锐角三角形中的对边与斜边之间的比例关系。

设锐角为θ，对边长度为a，斜边长度为h，则正弦函数的定义为sinθ = a/h。

正弦函数的取值范围是[-1, 1]，当θ为0度时，正弦函数的值为0；当θ为90度时，正弦函数的值为1。

2. 余弦函数（cosine function）余弦函数也是锐角三角函数中常用的一种函数，它表示了锐角三角形中的邻边与斜边之间的比例关系。

设锐角为θ，邻边长度为b，斜边长度为h，则余弦函数的定义为cosθ = b/h。

余弦函数的取值范围也是[-1, 1]，当θ为0度时，余弦函数的值为1；当θ为90度时，余弦函数的值为0。

3. 正切函数（tangent function）正切函数是锐角三角函数中最特殊的一种函数，它表示了锐角三角形中的对边与邻边之间的比例关系。

设锐角为θ，对边长度为a，邻边长度为b，则正切函数的定义为tanθ = a/b。

正切函数的取值范围是(-∞, +∞)，当θ为0度时，正切函数的值为0；当θ为45度时，正切函数的值为1。

锐角三角函数在数学和物理中有着广泛的应用。

例如，在三角函数的图像中，正弦函数和余弦函数是周期函数，它们的图像呈现出波浪形状，常用于描述周期性的现象；而正切函数则常用于描述角度的变化率，例如在物体运动的分析中。

除了上述三种常见的锐角三角函数外，还有其余的三角函数，如余切函数、正割函数和余割函数，它们的定义和性质与前述三种函数类似，但使用频率相对较低。

在实际问题中，锐角三角函数可以用于解决各种与角度相关的计算和分析问题。

例如，可以利用正弦函数计算在斜面上物体的下滑速度，利用余弦函数计算在斜面上物体的压力分量，利用正切函数计算两个物体之间的相对速度等等。

初三常用三角函数值表
在初中数学学习中，三角函数是一个非常重要的概念，而
三角函数值表则是初学者经常需要掌握的内容之一。

三角函数包括正弦、余弦和正切三种函数，它们在不同角度下的取值可以通过表格形式展示，方便学生查找和运用。

在初三阶段，学生通常需要熟记特定角度下的三角函数值，这对于解决三角函数问题和推导公式都有很大帮助。

正弦函数值表
角度0°30°45°60°90°
正弦值00.5√2/2√3/21
余弦函数值表
角度0°30°45°60°90°
余弦值1√3/2√2/20.50
正切函数值表
角度0°30°45°60°90°
正切值0√3/31√3不存在
通过上面的三角函数值表，我们可以看到在常见角度下，
正弦、余弦和正切函数的取值情况。

这些数值是通过三角函数的定义和几何图形推导得到的，对于初三学生来说，熟练掌握这些数值对于解答题目是非常有帮助的。

同时，这些数值也在实际生活和工程领域中有着广泛的应用，比如在建筑、航海、天文学等领域都会用到三角函数的概念和数值。

除了常用的角度下的数值，还有一些其他角度下的三角函
数值也是初中阶段需要记住的，比如120°、150°、210°、240°等。

通过不断练习和记忆，学生可以更加熟练地运用三
角函数值，解决各种数学问题，为未来的学习打下坚实的基础。

希望初三的学生能够认真学习三角函数，掌握相关的数值表，提高数学水平，为未来的学习和发展奠定扎实的基础。

初中常用的三角函数值表
在初中数学学习中，三角函数是一个非常重要的概念。

三角函数在数学中起到了非常关键的作用，它们与角度的关系紧密联系在一起。

我们常用的三角函数包括正弦函数、余弦函数和正切函数，它们在初中阶段被广泛讨论和运用。

了解三角函数值的表格对于解题和理解三角函数的性质非常有帮助。

正弦函数值表
正弦函数是三角函数中的一个重要概念，它表示一个角的正弦值。

正弦函数的值域在-1到1之间变化，下表列出了一些常见角度对应的正弦函数值：
角度0°30°45°60°90°
正弦值01/2√2/2√3/21
余弦函数值表
余弦函数是另一个常用的三角函数，它表示一个角的余弦值。

余弦函数的值域也在-1到1之间，下表列出了一些常见角度对应的余弦函数值：
角度0°30°45°60°90°
余弦值1√3/2√2/21/20
正切函数值表
正切函数是三角函数中的另一个重要概念，它表示一个角的正切值。

正切函数的值可以是任意的实数，下表列出了一些常见角度对应的正切函数值：
角度0°30°45°60°90°
正切值0√3/31√3无穷大
通过上述三角函数的值表，我们可以看到不同角度对应的正弦、余弦和正切函数值的关系。

这些数学概念在几何学、物理学等领域中有着广泛的应用，掌握它们有助于我们更深入地理解数学知识。

在初中阶段，三角函数值表是一个重要的学习工具，帮助我们更好地理解和运用三角函数的性质和特点。