23.1 3.一般锐角的三角函数值

第23章 解直角三角形23.1 锐角的三角函数2 30°，45°，60°角的三角函数值教学目标经历探索30°，45°，60°角的三角函数值的过程，熟练进行计算，使学生理解正、余弦关系式及推导过程，并能利用其解答一些基本问题.教学重难点重点：能够进行含30°，45°，60°角的三角函数值的计算. 难点：进一步体会三角函数的意义. 教学过程 旧知回顾【问题】如图所示，在Rt △ABC 中，∠C ＝90°， (1)sin A ＝a c ，cos A ＝b c ，tan A ＝a b ，sin B ＝b c ，cos B ＝a c ，tan B ＝b a. (2)若∠A ＝30°，则a c ＝12.新课讲授【问题】问题1 如何得出30°，60°角的三角函数值？【活动】学生独立思考，回答. 如图，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，∠B ＝60°，设BC ＝1，则AB ＝2，由勾股定理得AC ＝ 3.于是可得sin 30°＝12，cos 30°＝32，tan 30°＝33，sin 60°＝32，cos 60°＝12，tan 60°＝3.【问题】问题2 如何得出45°角的三角函数值？ 【活动】学生独立思考，回答.如图，在Rt △ABC 中，∠C ＝90°，∠A ＝∠B ＝45°，设BC ＝1，则AC ＝1，AB ＝2，于是有sin 45°＝22，cos 45°＝22，tan 45°＝1.教学反思教学反思【互动】学生独立完成，代表回答，教师补充完善.例1 求下列各式的值：（1）2sin603tan30tan45︒+︒+︒；（2）2cos45tan60cos30︒+︒︒.解：（1）2sin603tan30tan45︒+︒+︒231=+1=.（2）2cos45tan60cos30︒+︒︒2=+1322=+2=.需要提醒学生注意：cos245°表示（cos 45°）2，sin245°表示（sin 45°）2，tan245°表示（tan 45°）2.例2 求下列各式的值：(1) cos260°＋cos245°＋2sin 30°sin 45°；(2)cos60sin45cos60sin45︒+︒︒-︒＋cos60cos45cos60cos45︒-︒︒+︒.学生独立完成，代表回答，教师补充完善，强化过程计算.解：(1)原式＝2212⎛⎫+⎪⎝⎭＋2×12×22＝14＋12＋12＝54；(2)原式＝12＋2212－22＋12－2212＋22＝（1＋2）2＋（1－2）212－（2）2教学反思＝1＋2＋22＋1－22＋21－2＝－6.【思考】从上面问题1、2的计算中，不难发现：sin 30° ＝cos 60°，sin 60° ＝cos 30°，sin 45° ＝ cos 45°.这就是说，30° ，45° ，60°角的正(余)弦的值，分别等于它们余角的余(正)弦的值.这个规律，是否适合任意一个锐角呢? 解：任意一个锐角的正(余)弦值，等于它的余角的余(正)弦值.如图，在Rt △ABC 中，∠C ＝90°.∵ sin A ＝a c ，cos A ＝b c ，sin B ＝b c ，cos B ＝a c ， ∴ sin A ＝cos B ，cos A ＝sin B .∵ ∠A ＋∠B ＝90°，∴ ∠B ＝90°－∠A ，即 sin A ＝cos B ＝cos (90°－∠A )， cos A ＝sin B ＝sin (90°－∠A ).【归纳】 结论：任意一个锐角的正(余)弦值，等于它的余角的余(正)弦值. 典型例题 例3 填空：(1)已知sin 67°28′＝0.923 7，则cos 22°32′＝0.923 7；(2)已知cos 4°14′＝0.997 3，则sin 85°46′＝0.997 3. 例4 已知sin A ＝12，且∠B ＝90°－∠A ，求cos B . 解：∵ ∠B ＝90°－∠A ，∴ ∠A ＋∠B ＝90°， ∴ cos B ＝cos (90°－∠A )＝sin A ＝12.变式：已知α，β为锐角，且sin (90°－α)＝13，sin β＝14，求cos(90)cos ββ︒-的值. 解：∵ sin (90°－α)＝cos α＝13，cos (90°－β)＝sin β＝14， ∴ cos(90)cos ββ︒-＝1413＝34.课堂练习教学反思1.(1)在△ABC 中，sin B ＝cos (90°－∠C )＝12，那么△ABC 是 三角形；(2)已知α为锐角，tan (90°－α)＝3，则α的度数为 . 2.计算：(1)12sin 60°×22cos 45°；(2)tan 230°＋cos 230°－sin 245°tan 45°. 参考答案1.（1）等腰 （2）30°2. 解：(1)12sin 60°×22cos 45°＝12×32×22×22＝38；(2)tan 230°＋cos 230°－sin 245°tan 45°＝222+- ×1 ＝13＋34－12＝712. 学生独立完成，教师归纳解题思路：这类问题一般分两步完成，第一步把值准确地代入；第二步就是根据实数的混合运算顺序及法则进行计算.课堂小结布置作业教材第119页练习 T1，T2，第122页习题23.1 T1板书设计1. 特殊角的三角函数值2.例1， 例23.例3， 例44.练习。

高中完整的三角函数值表三角函数是数学中重要的概念之一，在高中数学课程中也是需要深入理解和掌握的内容。

三角函数除了具有数学概念外，更多地被应用于各种实际问题的求解中。

通过建立完整的三角函数值表，我们可以更好地理解三角函数在不同角度下的取值，从而为数学和实际问题的解决提供帮助。

三角函数简介三角函数是描述角度与边长之间关系的函数，常见的三角函数有正弦函数（sin）、余弦函数（cos）、正切函数（tan），它们分别表示直角三角形中某个角的对应比值。

在单位圆中，角度和三角函数值之间的关系被广泛运用。

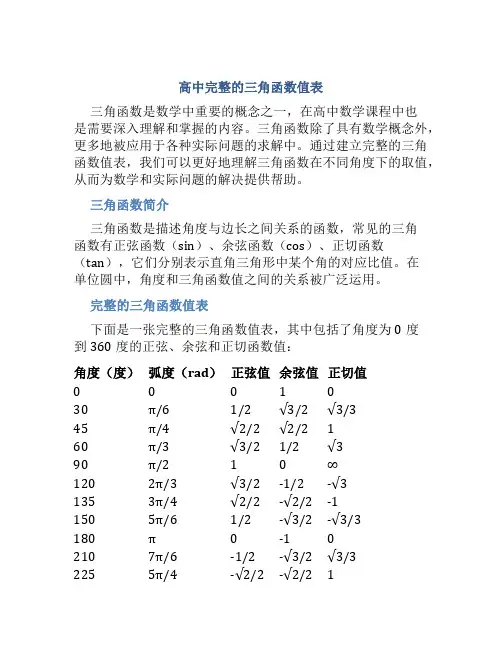
完整的三角函数值表下面是一张完整的三角函数值表，其中包括了角度为0度到360度的正弦、余弦和正切函数值：角度（度）弧度（rad）正弦值余弦值正切值0001030π/61/2√3/2√3/345π/4√2/2√2/2160π/3√3/21/2√390π/210∞1202π/3√3/2-1/2-√31353π/4√2/2-√2/2-11505π/61/2-√3/2-√3/3180π0-102107π/6-1/2-√3/2√3/32255π/4-√2/2-√2/212404π/3-√3/2-1/2√32703π/2-10∞3005π/3-√3/21/2-√33157π/4-√2/2√2/2-133011π/6-1/2√3/2-√3/33602π010总结通过建立完整的三角函数值表，我们可以更好地理解三角函数在不同角度下的取值规律。

这些数值可以帮助我们快速计算角度对应的正弦、余弦和正切值，为解决数学问题提供帮助。

在学习三角函数和解决实际问题时，深入理解三角函数值表将有助于我们更好地掌握相关知识。

通过一个个数值的对比和推导，我们可以看到三角函数之间的关系以及它们在不同角度下的变化规律。

这些都是我们学习三角函数不可或缺的部分，希望这份三角函数值表能够对你的学习和理解有所帮助。

23.1.3一般锐角的三角函数值知识点1用计算器求锐角的三角函数值1．利用计算器计算sin30°时，依次按键sin30＝，显示的结果是()A．0.5 B．0.707 C．0.866 D．12．用计算器计算cos44°的结果(精确到0.01)是()A．0.90 B．0.72 C．0.69 D．0.663．用计算器求下列三角函数值(精确到0.0001)：(1)sin75.6°；(2)cos37.1°；(3)tan25°.知识点2用计算器求锐角的度数4．2018·淄博一辆小车沿着如图23－1－34所示的斜坡向上行了100米，其铅直高度上升了15米．在用科学计算器求坡角α的度数时，具体按键顺序是()图23－1－34图23－1－355．已知三角函数值，用计算器求锐角A.(角度精确到1″)(1)sin A＝0.3035；(2)cos A＝0.1078；(3)tan A＝7.5031.知识点3锐角三角函数的增减与取值范围6．三角函数值sin30°，cos16°，cos43°之间的大小关系是()A．cos43°＞cos16°＞sin30°B．cos16°＞sin30°＞cos43°C．cos16°＞cos43°＞sin30°D．cos43°＞sin30°＞cos16°7．若45°＜α＜90°，则sinα________cosα；若0°＜α＜45°，则sinα________cos α.(填“>”“<”或“＝”)8．用不等号连接下面的式子：(1)tan19°________tan21°；(2)cos18°________sin18°.9．若α为锐角，且cosα＜1，则α的取值范围是__________．10．若α是锐角，且sinα＝1－2m，则m的取值范围是________．11．计算sin0°＋cos0°＋tan0°＋sin90°＋cos90°的结果为()A．0 B．1 C．2 D．312．在△ABC中，∠C＝90°，设sin B＝n，当∠B是最小的内角时，n的取值范围是()A．0<n<22B．0<n<12C．0<n<33D．0<n<3213．若α＜60°，且sin(60°－α)＝0.75，则cos(30°＋α)＝________．14．如图23－1－36，在△ABC中，AB＝AC＝10，BC＝13，求△ABC的三个内角的度数．(精确到l′)图23－1－3615．设β为任意锐角，你能说明tanβ与sinβ之间的大小关系吗？若能，请比较大小；若不能，请说明理由．16．2017·福建小明在某次作业中得到如下结果：sin27°＋sin283°≈0.122＋0.992＝0.9945，sin222°＋sin268°≈0.372＋0.932＝1.0018，sin229°＋sin261°≈0.482＋0.872＝0.9873，sin237°＋sin253°≈0.602＋0.802＝1.0000，sin245°＋sin245°＝(22)2＋(22)2＝1.据此，小明猜想：对于任意锐角α，均有sin2α＋sin2(90°－α)＝1.(1)当α＝30°时，验证sin2α＋sin2(90°－α)＝1是否成立．(2)小明的猜想是否成立？若成立，请给予证明；若不成立，请举出一个反例．17．(1)如图23－1－37①所示，已知AB1＝AB2＝AB3，B1C1⊥AC于点C1，B2C2⊥AC于点C2，B3C3⊥AC于点C3，试比较sin∠B1AC，sin∠B2AC和sin∠B3AC的值的大小；(2)如图②所示，在Rt△ACB3中，B1和B2是线段B3C上的点(与点B3，C不重合)，试比较cos∠B1AC，cos∠B2AC和cos∠B3AC的值的大小；(3)总结(1)(2)中的规律，根据你探索到的规律试比较18°，34°，50°，62°，88°这些锐角的正弦值的大小和余弦值的大小．图23－1－37教师详解详析1．A2．B [解析] 本题要求熟练应用计算器，对计算器显示的结果，根据近似数的概念用四舍五入法取近似数．3．[解析] 以度为单位的锐角，按sin ，cos ，tan 键后直接输入数字，再按＝得到锐角的正弦，余弦，正切值．解：(1)按sin 7 5 . 6 ＝显示0.968583161，即sin75.6°≈0.9686.(2)按cos 3 7 . 1＝显示0.797583928，即cos37.1°≈0.7976.(3)按tan 2 5＝显示0.466307658，即tan25°≈0.4663.4．A5．解：(1)∠A≈17°40′5″.(2)∠A≈83°48′41″.(3)∠A≈82°24′30″.6．C [解析] 根据余角三角函数之间的关系，sin30°＝ cos60°，而cos16°＞cos43°＞cos60°，即cos16°＞cos43°＞ sin30°.7．＞ ＜ [解析] (方法一)取特殊值法：当45°＜α＜90°时，取α＝60°，sin60°＝32，cos60°＝12，此时sin60°＞cos60°，因此应填“＞”；当0°＜α＜45°时，取α＝30°，sin30°＝12，cos30°＝32，由sin30°＜cos30°，此时sinα＜cosα，应填“＜”． (方法二)统一转化为正弦，利用锐角的正弦值随着角度的增大而增大比较．∵cosα＝sin(90°－α)(α为锐角)，当45°＜α＜90°时，α＞90°－α，∴sinα＞sin(90°－α)，∴sinα＞cosα；当0°＜α＜45°时，α＜90°－α，∴sinα＜sin(90°－α)，∴sinα＜cosα.8．(1)＜ (2)＞ [解析] (1)由于正切值随锐角的增大而增大，因为19°＜21°，所以tan19°＜tan21°，应填“＜”．(2)由cos18°＝sin(90°－18°)＝sin72°，因为72°＞18°，所以sin72°＞sin18°，即cos18°＞sin18°.9．0°＜α＜90°10．0＜m ＜12 [解析] 由题意可知0＜1－2m ＜1，解得0＜m ＜12. 11．C12．A [解析] 根据题意，知0°＜∠B ＜45°，再根据sin45°＝22和一个锐角的正弦值随着角度的增大而增大进行分析，有0＜n ＜22.故选A. 13．0.75 [解析] cos(30°＋α)＝cos[90°－(60°－α)]＝sin(60°－α)＝0.75.14．解：如图，过点A 作BC 边上的高AD ，则BD ＝CD ＝6.5，∠BAD ＝∠CAD ＝12∠BAC.在Rt △ABD 中，sin ∠BAD ＝BD AB ＝6.510＝0.65， ∴∠BAD≈40°32′，∴∠BAC ＝2∠BAD≈81°4′，∴∠B ＝∠C≈49°28′.15．[解析] 根据正切和正弦的定义列出表达式，再根据直角三角形的斜边大于直角边，判断出 AC BC 和 AC AB 的大小． 解：能．如图，设β是Rt △ABC 的一个锐角，令∠B ＝β，则tanβ＝AC BC ，sinβ＝AC AB.因为BC<AB ，所以AC BC >AC AB，所以tanβ＞sinβ.16．解：(1)当α＝30°时，sin 2α＋sin 2(90°－α)＝sin 230°＋sin 260°＝(12)2＋(32)2＝1. (2)小明的猜想成立，证明如下：如图，在△ABC 中，∠C ＝90°，设∠A ＝α，则∠B ＝90°－α.∴sin 2α＋sin 2(90°－α)＝(BC AB )2＋(AC AB )2＝BC 2＋AC 2AB 2＝AB 2AB 2＝1.17．解：(1)在题图①中，显然有B 1C 1＞B 2C 2＞B 3C 3，∵sin ∠B 1AC ＝B 1C 1AB 1，sin ∠B 2AC ＝B 2C 2AB 2， sin ∠B 3AC ＝B 3C 3AB 3，AB 1＝AB 2＝AB 3， ∴sin ∠B 1AC ＞sin ∠B 2AC ＞sin ∠B 3AC.(2)在Rt △ACB 3中，∠C ＝90°，cos ∠B 1AC ＝AC AB 1，cos ∠B 2AC ＝AC AB 2， cos ∠B 3AC ＝AC AB 3， ∵AB 3＞AB 2＞AB 1，∴AC AB 1＞AC AB 2＞AC AB 3， 即cos ∠B 1AC>cos ∠B 2AC>cos ∠B 3AC.(3)规律：锐角的正弦值随角度的增大而增大，锐角的余弦值随角度的增大而减小． 由规律可知：sin18°<sin34°<sin50°<sin62°<sin88°；cos18°>cos34°>cos50°>cos62°>cos88°.。

沪科版数学九年级上册23.1《锐角的三角函数》教学设计4一. 教材分析《锐角的三角函数》是沪科版数学九年级上册第23.1节的内容。

本节主要介绍了锐角三角函数的定义及应用。

通过本节的学习，学生能够理解锐角三角函数的概念，掌握锐角三角函数的计算方法，并能够运用锐角三角函数解决实际问题。

二. 学情分析九年级的学生已经学习了三角函数的基础知识，对函数的概念和性质有一定的了解。

但是，对于锐角三角函数的具体定义和应用，学生可能还比较陌生。

因此，在教学过程中，需要引导学生从实际问题出发，逐步理解和掌握锐角三角函数的概念和计算方法。

三. 教学目标1.了解锐角三角函数的定义及计算方法。

2.能够运用锐角三角函数解决实际问题。

3.培养学生的数学思维能力和解决问题的能力。

四. 教学重难点1.锐角三角函数的定义及计算方法。

2.运用锐角三角函数解决实际问题。

五. 教学方法1.情境教学法：通过设置实际问题，引导学生从实际问题中抽象出锐角三角函数的概念。

2.案例教学法：通过具体的案例，讲解和演示锐角三角函数的计算方法。

3.小组合作学习：学生分组讨论和解决问题，培养学生的合作意识和团队精神。

六. 教学准备1.教学课件：制作课件，展示锐角三角函数的定义和计算方法。

2.案例材料：准备一些实际的案例，用于讲解和演示锐角三角函数的应用。

3.练习题：准备一些练习题，用于巩固学生的学习成果。

七. 教学过程1.导入（5分钟）利用课件展示一些实际的例子，如建筑物的角度测量、滑翔机的起飞角度等，引导学生思考这些例子与三角函数的关系，从而引出锐角三角函数的概念。

2.呈现（10分钟）讲解锐角三角函数的定义和计算方法，引导学生从实际问题中抽象出锐角三角函数的概念。

3.操练（10分钟）学生分组讨论和解决一些实际的案例，如滑翔机的起飞角度问题、房屋建筑的倾斜度问题等，巩固学生对锐角三角函数的理解和应用。

4.巩固（10分钟）学生独立完成一些练习题，检测学生对锐角三角函数的掌握程度。

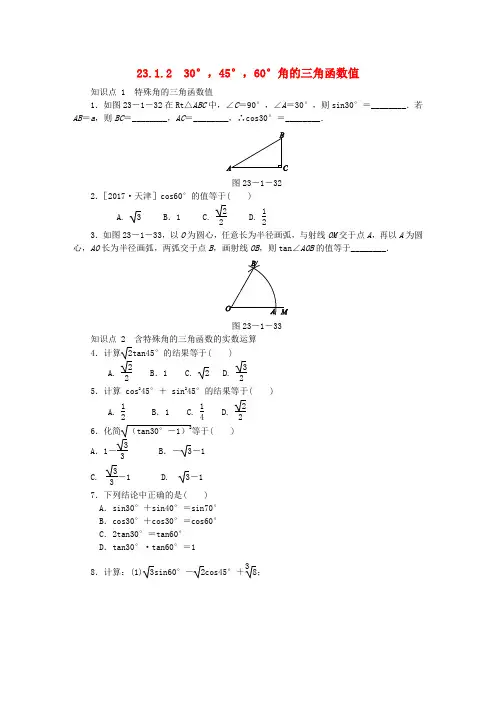
23.1.2 30°，45°，60°角的三角函数值知识点 1 特殊角的三角函数值1．如图23－1－32在Rt △ABC 中，∠C ＝90°，∠A ＝30°，则sin30°＝________．若AB ＝a ，则BC ＝________，AC ＝________，∴cos30°＝________．图23－1－322．［2017·天津］cos60°的值等于( )A. 3 B ．1 C.22 D. 123．如图23－1－33，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则tan ∠AOB 的值等于________．图23－1－33知识点 2 含特殊角的三角函数的实数运算 4．计算2tan45°的结果等于( )A.22 B ．1 C. 2 D. 325．计算 cos 245°＋ sin 245°的结果等于( )A. 12 B ．1 C. 14 D. 22 6．化简（tan30°－1）2等于( ) A ．1－33B ．－3－1 C.33－1 D. 3－1 7．下列结论中正确的是( ) A ．sin30°＋sin40°＝sin70° B ．cos30°＋cos30°＝cos60° C ．2tan30°＝tan60° D ．tan30°·tan60°＝18．计算：(1)3sin60°－2cos45°＋38；(2)sin60°cos30°－（1－tan60°）2；(3)tan30°＋cos60°sin60°；(4)2sin45°－|－2|－(－2018)0＋(13)－1＋3tan30°.知识点 3 已知三角函数值求特殊角9．已知tan A ＝1，则锐角A 的度数是( ) A ．30° B ．45° C ．60° D ．75°10．在Rt △ABC 中，∠C ＝90°，如果cos B ＝12，那么∠A 等于( )A ．15°B ．30°C ．45°D ．60°11．在△ABC 中，若⎪⎪⎪⎪⎪⎪sin A －12＋(33－tan B )2＝0，且∠A ，∠B 为锐角，则∠C 的度数为( )A ．30°B ．60°C ．90°D ．120°12．若α为锐角，当11－tan α无意义时，sin(α＋15°)＋cos(α－15°)的值为________．13．若tan A 的值是方程x 2－(1＋3)x ＋3＝0的一个根，求锐角A 的度数．14．点M (－sin60°，－cos60°)关于x 轴对称的点的坐标是( ) A ．(32，12) B ．(－32，－12)C ．(－32，12) D ．(－12，－32) 15．［2016·宿州二模］已知α，β均为锐角，且满足⎪⎪⎪⎪⎪⎪sin α－12＋（tan β－1）2＝0，则α＋β＝________°.16．［2016·临沂］一般地，当α，β为任意角时，sin(α＋β)与sin(α－β)的值可以用下面的公式求得：sin(α＋β)＝sin αcos β＋cos αsin β； sin(α－β)＝sin αcos β－cos αsin β.例如：sin90°＝sin(60°＋30°)＝sin60°cos30°＋cos60°sin30°＝32×32＋12×12＝1. 类似地，可以求得sin15°的值是________．17．等腰三角形的底边长为20 cm ，面积为100 33 cm 2，求它的各内角的度数．18．如图23－1－34，等边三角形ABC 中，D ，E 分别为AB ，BC 边上的点，且AD ＝BE ，AE 与CD 交于点F ，AG ⊥CD 于点G ，求AGAF的值．图23－1－3419．如图23－1－35，在△ABC 中，a ，b ，c 分别为∠A ，∠B ，∠C 的对边．若∠B ＝60°，则ca＋b＋ab＋c的值为( )A.12B.22C．1D. 2图23－1－3520．如图23－1－36，在Rt△ABC中，∠C＝90°，AC＝8，AD为∠BAC的平分线，AD＝16 33，求∠B的度数及边BC，AB的长．图23－1－36教师详解详析1. 12 12a 32a 322. D3. 3 [解析] 连接AB.由题意知，△ABO 是等边三角形，故∠AOB＝60°，∴tan ∠AOB ＝ 3.4．C [解析] 把tan 45°＝1代入原式进行计算，即原式＝2×1＝ 2.故选C . 5．B [解析] cos 45°＝sin 45°＝22，代入原式，得cos 245°＋sin 245°＝(22)2＋(22)2＝12＋12＝1.故选B . 6．A [解析] ∵tan 30°＝33<1, ∴tan 30°－1＜0，∴（tan 30°－1）2＝1－tan 30°＝1－33. 7．D8．解：(1)3sin 60°－2cos 45°＋38 ＝3×32－2×22＋2＝52. (2)原式＝3232－（1－3）2＝1－3＋1＝2－ 3.(3)tan 30°＋cos 60°sin 60°＝(33＋12)÷32＝23＋33.(4)原式＝2×22－2－1＋3＋3×33＝2－2－1＋3＋3＝2＋ 3. 9．B [解析] ∵tan A ＝1，∠A 为锐角，tan 45°＝1，∴∠A ＝45°.10．B [解析] ∵在Rt △ABC 中，∠C ＝90°，cos B ＝12，∴∠B ＝60°，∴∠A ＝180°－∠C－∠B＝30°.故选B .11．D12. 3 [解析] 由已知得α＝45°，再代入计算．13．解：解方程x 2－(1＋3)x ＋3＝0， 得x 1＝1，x 2＝ 3.由题意，知tan A ＝1或tan A ＝3， ∴∠A ＝45°或∠A＝60°. 14． C[解析] 关于x 轴对称的两点的坐标特征：横坐标相同，纵坐标互为相反数． 15． 75[解析] ∵⎪⎪⎪⎪⎪⎪sin α－12＋（tan β－1）2＝0，∴sin α＝12，tan β＝1.∵α，β均为锐角，∴＝30°，β＝45°.∴α＋β＝30°＋45°＝75°. 故答案为75. 16．6－2417．解：如图．在△ABC 中，AB ＝AC ，BC ＝20 cm .设等腰三角形底边上的高AD 为x cm ，底角为α， 则有12x·20＝100 33，解得x ＝10 33.∵tan α＝10 3310＝33，∴α＝30°，∴顶角为180°－2×30°＝120°.∴该等腰三角形的三个内角的度数分别为30°，30°，120°. 18．解：在△CAD 与△ABE 中， ∵⎩⎪⎨⎪⎧AC ＝AB ，∠CAD ＝∠ABE＝60°，AD ＝BE ， ∴△CAD ≌△ABE ， ∴∠ACD ＝∠BAE.∵∠BAE ＋∠CAE＝60°， ∴∠ACD ＋∠CAE＝60°，∴∠AFG ＝∠ACD＋∠CAE＝60°. 在Rt △AFG 中， ∵sin ∠AFG ＝AGAF ，∴AG AF ＝32. 19．C [解析] 如图，过点A 作AD⊥BC 于点D.在Rt △BDA 中，∵∠B ＝60°， ∴DB ＝c 2，AD ＝3c 2.在Rt △ADC 中，DC 2＝AC 2－AD 2，∴(a －c 2)2＝b 2－34c 2，即a 2＋c 2＝b 2＋ac ，∴c a ＋b ＋a b ＋c ＝c 2＋cb ＋a 2＋ab （a ＋b ）（b ＋c ）＝a 2＋c 2＋ab ＋bcac ＋ab ＋bc ＋b2＝1.20．解：在Rt △ACD 中， ∵cos ∠CAD ＝AC AD ＝816 33＝32，且∠CAD 为锐角， ∴∠CAD ＝30°.∵AD 为∠BAC 的平分线， ∴∠BAD ＝∠CAD＝30°， 即∠CAB＝60°，∴∠B ＝90°－∠CAB＝30°. ∵sin B ＝ACAB ，∴AB ＝ACsin B ＝8sin 30°＝16. 又∵cos B ＝BCAB ，∴BC ＝AB·cos B ＝16×32＝8 3.。