高频课本例题

例1-1-1 如例图1-1-1所示电路。

已知H L μ=586，Ｃ＝200pF, Ω=12r ，s R 和L R 分别为信号源内阻和负载电阻。

试求：未接入s R 、L R 时和s R 、L R 都等于200K Ω时，回路的等效品质因数、谐振电阻、通频带。

解：(1) 未接入s R 、L R 时46510200105862121126P =⨯⨯⨯==--ππLCf (kHz)k Ω244121020010586 126P =⨯⨯⨯==--C r L R 由式(1-1-24)有：143121020010586126P =⨯⨯==--rQ ρ3.3143456BW P P 7.0===Q f (kHz) (2) 接入200==L s R R k Ω时将图(a) 变换为图(b)所示电路，其中244P =R k Ω，并联谐振回路的等效损耗电导由式(1-1-33)得：014.0111Ls P =++=R R R G (mS ) 由式(1-3-34)得：56.411020010586014.0111126P L =⨯⨯===--G LG Q ρω所以 2.1156.41465BW L P 7.0===Q f (kHz) 从计算结果可以看到，接入信号源和负载时，回路的Ｑ值降低，通频带变宽。

例1-1-2 某收音机的中频放大器，其选频回路中心频率p f =465 kHz ．BW 0.7=8 kHz ，并联回路电容C=220pF ，试计算回路电感和L Q 值。

若电感线圈的100p =Q ，问在回路上应并联多大的电阻才能满足要求。

解： (1) 由LC f π21P =得(mH) 533.010220)104652(1)2(112232p ≈⨯⨯⨯⨯⨯==-ππC f L 由式(1-1-24) .615510220104652100123P pp ≈⨯⨯⨯⨯==-πωCQ R )(k Ω由Lp 7.0BW Q f =得 125.5810810465BW 337.0p L =⨯⨯==f Q (2) 若100p =Q ，令回路并联电阻为L R ，由式(1-34)得LP Pp P L 11R R Q GC LG Q +===ωω )(k 216)1125.58100/(6.155)1(Lp p L Ω≈-=-=Q Q R R ，可以取标称电阻k Ω 022L =R 。

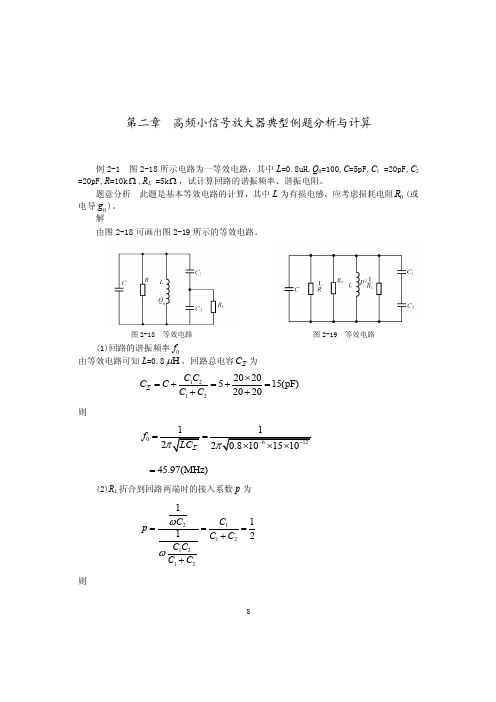
8第二章 高频小信号放大器典型例题分析与计算例2-1 图2-18所示电路为一等效电路，其中L =0.8uH,Q 0=100,C =5pF,C 1 =20pF,C 2 =20pF,R =10k Ω,R L =5k Ω，试计算回路的谐振频率、谐振电阻。

题意分析 此题是基本等效电路的计算，其中L 为有损电感，应考虑损耗电阻0R (或电导0g )。

解由图2-18可画出图2-19所示的等效电路。

图2-18 等效电路 图2-19 等效电路(1)回路的谐振频率0f由等效电路可知L =0.8H μ，回路总电容C ∑为12122020515(pF)2020C C C C C C ∑⨯=+=+=++则0f ==45.97(MHz)=(2)R L 折合到回路两端时的接入系数p 为211212121112C C p C C C C C C ωω===++则9()2233110.50.0510s 510L P R -=⨯=⨯⨯ 电感L 的损耗电导0g 为0660011245.97100.810100g LQ ωπ-==⨯⨯⨯⨯⨯ ()643.3010s -=⨯总电导 23-3031110.0433100.05101010L g g P R R ∑-=++=+⨯+⨯⨯ ()30.193310s -=⨯谐振电阻 ()P 1 5.17k R g ∑==Ω例2-2 有一个RLC 并联谐振电路如图2-20所示，已知谐振频率f 0=10MHz,L =4μH ,Q 0=100,R =4k Ω。

试求(1)通频带20.7f ∆;(2)若要增大通频带为原来的2倍，还应并联一个多大电阻?题意分析 此题是一个RLC 并联谐振电路的基本计算，了解通频带的变化与回路电阻的关系。

解 (1)计算通频带电感L 的损耗电导0g 为 图2-20 RLC 并联谐振回路066001121010410100g LQ ωπ-==⨯⨯⨯⨯⨯()639.810s -=⨯回路总电导6031139.810410g g R ∑-=+=+⨯⨯ ()6289.810s -=⨯10回路的有载品质因数L Q 为666011g 21010410289.810L Q L ∑ωπ--==⨯⨯⨯⨯⨯⨯13.74=回路通频带()()6600.7101020.72810Hz 0.728MHz 13.74L f f Q ∆⨯===⨯= (2)若通带增大一倍，即20.71.456MHz f ∆=，计算应再并多大电阻R '根据题意要求通频带增大一倍，则回路的有载品质因数应减小一倍，即16.872LL Q Q '== 对应的'g ∑应该增大一倍，即 ()6'2579.610s g g ∑∑-==⨯ 因为0'11g g R R∑=++' 所以0''11g g g g R R ∑∑∑⎛⎫=-+=- ⎪'⎝⎭()6289.810s -=⨯则 3.45k R '=Ω图2-21 单调谐放大电路11例2-3 单调谐放大器如图2-21所示。

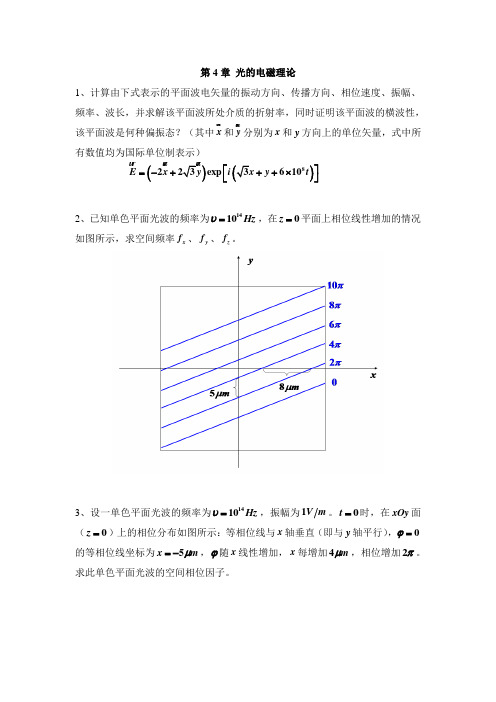
第4章 光的电磁理论1、计算由下式表示的平面波电矢量的振动方向、传播方向、相位速度、振幅、频率、波长，并求解该平面波所处介质的折射率，同时证明该平面波的横波性，该平面波是何种偏振态？（其中x 和y 分别为x 和y 方向上的单位矢量，式中所有数值均为国际单位制表示）())8223exp 610E x y i y t ⎡⎤=-+++⨯⎣⎦ 2、已知单色平面光波的频率为1410Hz υ=，在0z =平面上相位线性增加的情况如图所示，求空间频率x f 、y f 、z f 。

3、设一单色平面光波的频率为1410Hz υ=，振幅为1V m 。

0t =时，在xOy 面（0z =）上的相位分布如图所示：等相位线与x 轴垂直（即与y 轴平行），0ϕ=的等相位线坐标为5x m μ=-，ϕ随x 线性增加，x 每增加4m μ，相位增加2π。

求此单色平面光波的空间相位因子。

4、试确定下列各组光波表达式所代表的偏振态：（1）、()0si n x E E t k z ω=-，()0cos y E E t kz ω=- （2）、()0co s x E E t k z ω=-，()0cos 4y E E t kz ωπ=-+ （3）、()0si n x E E t kz ω=-，()0sin y E E t kz ω=--5、若要使自然光经过红宝石（ 1.76n =）表面反射后成为完全偏振光，入射角应等于多少？求在此入射角的情况下，折射光的偏振度t P 。

6、如图所示，玻璃块周围介质（水）的折射率为1 1.33n =。

若光束射向玻璃块的入射角为45，问玻璃块的折射率至少应为多大才能使透入光束发生全反射。

7、如图所示，光束垂直入射到45直角棱镜的一个侧面，经斜面反射后从第二个侧面透出。

若入射光强为0I ，问从棱镜透出的光束的强度为多少？（设棱镜的折射率为1.52，棱镜周围为空气，并且不考虑棱镜的吸收）8、穆尼棱体能将偏振方向与入射面成45的线偏振光变成圆偏振光，如图所示。

人教版初中数学二元一次方程组高频考点例题解析单选题1、下列方程中属于三元一次方程的是（）A．π+x+y=6B．xy+y+z=7C．x+2y−3z=9D．3x+2y−4z=4x+2y−2z答案：C解析：根据三元一次方程的定义：含有三个未知数，并且最高项的次数是1的整式方程，由此进行判断．A选项：只有2个未知数，故不是三元一次方程；B选项：最高项的次数为2，故不是三元一次方程；C选项：x+2y−3z=9，是三元一次方程；D选项：化简后2有2个未知数，故不是三元一次方程；故选：C.小提示：考查了三元一次方程的定义，判断一个方程是不是三元一次方程需要注意以下几点：①方程中含有三个未知数，与对应；②方程中所含三个未知数的项的次数都是1，与“一次”对应；③等号两边的代数式都是整式；④判断一个方程是不是三元次方程，先要对这个方程进行整理；⑤三元一次方程都能整理成ax+by+cz=k (a≠0,b≠0c≠0)的形式.2、如果二元一次方程组{x+y=ax−y=4a的解是二元一次方程3x−5y−30=0的一个解，那么a的值是（）．A．3B．2C．7D．6答案：B解析：利用如下所示的②×4-①，可得4x−4y−x−y=16a−a即3x−5y=15a，再由3x−5y−30=0进行求解即可．解：{x+y=a①x−y=4a②由②×4-①，可得4x−4y−x−y=16a−a即3x−5y=15a，∵二元一次方程组{x+y=ax−y=4a的解是二元一次方程3x−5y−30=0的一个解，∴3x−5y−30=0即3x−5y=30，∴15a=30，∴a=2，故选B．小提示：本题主要考查了二元一次方程组的解，解题的关键在于能够利用整体代入的思想进行求解．3、一套数学题集共有100道题，甲、乙和丙三人分别作答，每道题至少有一人解对，且每人都解对了其中的60道．如果将其中只有1人解对的题称作难题，2人解对的题称作中档题，3人都解对的题称作容易题，那么下列判断一定正确的是（）A．容易题和中档题共60道B．难题比容易题多20道C．难题比中档题多10道D．中档题比容易题多15道答案：B解析：设容易题有a题，中档题有b题，难题有c题，根据“三种题型共100道，每道题至少有一人解对，且每人都解对了其中的60道”，即可得出关于a，b，c的三元一次方程组，用方程①×2-方程②，可求出c-a=20，即难题比容易题多20题，此题得解．解：设容易题有a 题，中档题有b 题，难题有c 题，依题意，得：{a +b +c =100①3a +2b +c =3×60② ①×2-②，得：c-a=20，∴难题比容易题多20题．故选：B ．小提示：本题考查了三元一次方程组的应用，找准等量关系，正确列出三元一次方程组是解题的关键．4、若方程组{3x +y =1+3a x +3y =1−a的解满足x +y ＝0，则a 的值为（ ） A ．﹣1B ．1C ．0D ．无法确定答案：A解析：解：方程组两方程相加得：4（x+y ）=2+2a ，即x+y=12（1+a ）， 由x+y=0，得到12（1+a ）=0，解得：a=-1．故选：A ．5、以方程组{x +y =2x −y =1的解为坐标的点（x ，y ）在平面直角坐标系中的位置是（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案：A解析：先求出方程组的解，然后即可判断点的位置．解：解方程组{x +y =2x −y =1， 得{x =1.5y =0.5， ∴点（1.5，0.5）在第一象限．故选：A ．小提示：本题考查了二元一次方程组的解法和坐标系中点的坐标特点，属于基本题型，解题的关键是熟练掌握上述基础知识．6、用代入消元法解方程组{3x +4y =2①2x −y =5②使得代入后化简比较容易的变形是( ) A ．由①得x =2−4y 3B ．由①得y =2−3x 4C ．由②得x =y+52D ．由②得y ＝2x －5答案：D解析： 根据代入消元法解二元一次方程组的步骤可知变形②更简单.解：观察方程①②可知，②中y 的系数为-1，比其它未知数的系数更为简单，所只要将②变形为y ＝2x －5③，再把③代入①即可求出方程组的解.故选D.小提示：本题考查了用代入消元法解二元一次方程组，理解代入消元法解方程组时化简系数较简单的方程是解题的关键.7、春节将至，某超市准备用价格分别是36元/kg和20元/kg的两种糖果混合成100kg的什锦糖出售，混合后什锦糖的价格是28元/kg．若设需要36元/kg的糖果x kg，20元/kg的糖果y kg，则下列方程组中能刻画这一问题中数量关系的是（）A．{x+y=10036x+20y=28B．{x+y=10036x+20y=28×100C．{x+y=10028x+28y=100×(36+20)D．{x+y=10020x+36y=28×100答案：B解析：由题意得等量关系：两种糖果混合成100kg的什锦糖；36元/kg的糖果x kg的费用＋20元/kg的糖果y kg的费用＝100kg×28，即可得出方程组．解：设需要36元/kg的糖果x kg，20元/kg的糖果y kg，由题意得：{x+y=10036x+20y=28×100故选：B．小提示：此题主要考查了由实际问题抽象出二元一次方程组，关键是正确理解题意，找出题目中的等量关系．8、若单项式2x2y a+b与-13x a-b y4是同类项，则a，b的值分别为( )A．a＝3，b＝1 B．a＝-3，b＝1C．a＝3，b＝-1D．a＝-3，b＝-1答案：A解析：试题分析：∵单项式2x2y a+b与−13x a−b y4是同类项，∴{a−b=2a+b=4，解得：a=3，b=1，故选A．考点：1．解二元一次方程组；2．同类项．填空题9、(黄石中考)一食堂需要购买盒子存放食物，盒子有A ，B 两种型号，单个盒子的容量和价格如表所示，现有15升食物需要存放且要求每个盒子要装满，由于A 型号盒子正做促销互动：购买三个及三个以上可一次性返现金4元，则购买盒子所需要最少费用为_______元．答案：29解析：设购买A 种型号盒子x 个,购买盒子所需要费用为y 元,则购买B 种盒子的个数为15−2x 3个,①当0≤x <3时,y =5x +15−2x3×6=x +30,∵k =1>0,∴y 随x 的增大而增大,∴当x =0时,y 有最小值,最小值为30元,②当3≤x 时,y =5x +15−2x3×6-4=26+x ,∵k =1>0,∴y 随x 的增大而增大,∴当x =3时,y 有最小值,最小值为29元,综合①②可得,购买盒子所需要最少费用为29元,故答案为29.10、已知三元一次方程组{x +y =3y +z =4x +z =5，则x +y +z =________．答案：6解析：方程组中三个方程左右两边相加，变形即可得到x+y+z 的值．解：{x +y =3y +z =4x +z =5 ①②③，①+②+③，得2x +2y +2z ＝12，∴x +y +z ＝6，故答案为:6．小提示：此题考查了解三元一次方程组，本题的技巧为将三个方程相加．11、一般地．含有______个未知数，并且含有未知数的项的最高次数是____次的_____方程叫二元一次方程． 答案： 两 一 整式解析：根据二元一次方程的定义直接可得答案.解：一般地．含有两个未知数，并且含有未知数的项的最高次数是一次的整式方程叫二元一次方程．所以答案是：两，一，整式.小提示：本题考查的是二元一次方程的定义，掌握定义是解题的关键.12、某水果基地为提高效益，对甲、乙、丙三种水果品种进行种植对比研究．去年甲、乙、丙三种水果的种植面积之比为5：3：2，甲、乙、丙三种水果的平均亩产量之比为6：3：5．今年重新规划三种水果的种植面积，三种水果的平均亩产量和总产量都有所变化．甲品种水果的平均亩产量在去年的基础上提高了50%，乙品种水果的平均亩产量在去年的基础上提高了20%，丙品种的平均亩产量不变．其中甲、乙两种品种水果的产量之比为3：1，乙、丙两种品种水果的产量之比为6：5，丙品种水果增加的产量占今年水果总产量的587，则三种水果去年的种植总面积与今年的种植总面积之比为______．答案：5:7##57解析：设去年甲、乙、丙三种水果的种植面积分别为：5x,3x,2x, 设去年甲、乙、丙三种水果的平均亩产量分别为：6a,3a,5a, 设今年的种植面积分别为：m,n,f, 再根据题中相等关系列方程：9a·m 3.6a·n =3①，3.6a·n 5a·f =65②，求解：m =1.2n,f =0.6n, 再利用丙品种水果增加的产量占今年水果总产量的587，列方程5a ·f −5a ·2x =587(9a ·m+3.6a·n+5a·f),求解x=15n,从而可得答案.解：∵去年甲、乙、丙三种水果的种植面积之比为5：3：2，设去年甲、乙、丙三种水果的种植面积分别为：5x,3x,2x,∵去年甲、乙、丙三种水果的平均亩产量之比为6：3：5，设去年甲、乙、丙三种水果的平均亩产量分别为：6a,3a,5a,则今年甲品种水果的平均亩产量为：6a×(1+50%)=9a,乙品种水果的平均亩产量为：3a(1+20%)=3.6a,丙品种的平均亩产量为5a,设今年的种植面积分别为：m,n,f,∵甲、乙两种品种水果的产量之比为3：1，乙、丙两种品种水果的产量之比为6：5，∴9a·m3.6a·n =3①，3.6a·n5a·f=65②，解得：m=1.2n,f=0.6n,又丙品种水果增加的产量占今年水果总产量的587，∴5a·f−5a·2x=587(9a·m+3.6a·n+5a·f),∴87×5a·0.6n−87×5a·2x=45a×1.2n+18an+15an,解得：x=15n,所以三种水果去年的种植总面积与今年的种植总面积之比为：10x m+n+f =2n1.2n+n+0.6n=57.所以答案是：5:7.小提示：本题考查的是三元一次方程组的应用，设出合适的未知数与参数，确定相等关系，建立方程组，寻求未知量之间的关系是解本题的关键.13、方程2x −3y =5,xy =3,x +3y =3,3x −y +2z =0,x 2+y =6中是二元一次方程的有___个．答案：1解析：二元一次方程满足的条件：整式方程；含有2个未知数；未知数的最高次项的次数是1．解：符合二元一次方程的定义的方程只有2x −3y ＝5； xy ＝3，x 2＋y ＝6的未知数的最高次项的次数为2，不符合二元一次方程的定义；x ＋3y ＝1不是整式方程，不符合二元一次方程的定义；3x −y ＋2z ＝0含有3个未知数，不符合二元一次方程的定义；由上可知是二元一次方程的有1个．所以答案是：1．小提示：主要考查二元一次方程的概念．要求熟悉二元一次方程的形式及其特点：含有2个未知数，未知数的最高次项的次数是1的整式方程．解答题14、我国古代数学著作《九章算术》中有这样一题，原文是：“今有大器五小器一容三斛，大器一小器五容二斛，问大小器各容几何．”意思是：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，是古代的一种容量单位），1个大桶加上5个小桶可以盛酒2斛．1个大桶、1个小桶分别可以盛酒多少斛？请解答．答案：1个大桶可以盛酒1324斛，1个小桶可以盛酒724斛．解析：直接利用5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛，分别得出等式组成方程组求出答案．解：设1个大桶可以盛酒x 斛，1个小桶可以盛酒y 斛，则{5x +y =3x +5y =2， 解得：{x =1324y =724， 答：1个大桶可以盛酒1324斛，1个小桶可以盛酒724斛． 小提示：此题主要考查了二元一次方程组的应用，正确得出等量关系是解题关键．15、小红在学校商店买了3支钢笔，1本练习本，2支中性笔共花13元，小颖买了2支钢笔，4本练习本，3支中性笔共花17元，小明打算在该商店买20支钢笔，20本练习本，20支中性笔寄给四川地震灾区的小朋友，他只有120元的压岁钱，请你帮他算一下，他的钱够吗？答案：120元的压岁钱够购买20支钢笔，20本练习本，20支中性笔．解析：设钢笔每支a 元，练习本b 元，中性笔c 元．利用题中已知条件列方程组{3a +b +2c =13①2a +4b +3c =17② ，由此可以求得(a +b +c )的值，所以通过比较20(a +b +c )与120的大小可以作出判断．设钢笔每支a 元，练习本b 元，中性笔c 元，则{3a +b +2c =13①2a +4b +3c =17②， ①+②得，5a +5b +5c =30所以，20a +20b +20c =4×30=120（元），即120元的压岁钱够购买20支钢笔，20本练习本，20支中性．。

初三化学高频考点例题专讲【例1】下列有关测定空气中氧气含量的说法不正确的是（）A．该实验可证明氧气约占空气总体积的 1/5
B．实验前一定要检查装置气密性
C．红磷燃烧一停止立即打开弹簧夹
D．实验时红磷一定要过量
【例2】做空气中实验、下列说法正确是（）
A．红磷燃烧时产生耀眼的白光
B．燃烧匙中的红磷可换成硫或木炭
C．集气瓶中剩余气体主要是稀有气体
D．通过此实验可知空气中氧气约占空气体积的 1/5
【例3】（2011•珠海）用如图装置测定空气中氧气的含量，物质R应该选用（）
A．铁片B．硫粉C．木炭D．红磷
【例4】为了空气中，某同学设计了如图所示实验，燃烧匙内装有红磷，若结果比实际空气中偏低，下列原因分析不可能是（）A．装置气密性不好
B．红磷太多
C．红磷太少
D．实验后集气瓶内温度没有冷却到室温
【例5】某同学用如图所示装置空气中，实验过程中发现低于 1/5 ．针对这一事实，你认为下列做法和想法不正确是（）
A．查看实验装置是否漏气
B．将红磷改为蜡烛再重做实验
C．红磷的量不足，瓶内氧气没有消耗完
D．未冷却至室温就打开弹簧夹，并观察进入水的体积
【例6】如图所示，用该装置测量空气中氧气的含量，在燃烧匙中加入红磷，红磷与氧气发生化学反应生成五氧化二磷，请按要求填空：
（1）在空气中点燃红磷，并迅速插入玻璃罩内，塞紧橡皮塞，此时看到的
主要现象是
，
该变化的文字表达式为。

（2）当红磷燃烧完毕，玻璃罩冷却到室温后，看到玻璃罩内水面的变化
是，出现该现象的原因是：红磷燃烧消耗了空气中的而
生成了固态的，从而使罩内的气体体
积，玻璃罩内气体压强玻璃罩外大气压。

高频复习题13答案一、选择题1. 下列哪个选项是正确的语法结构？A. 他昨天去了图书馆。

B. 他昨天图书馆去了。

C. 去了昨天图书馆他。

D. 图书馆昨天他去了。

答案：A2. 根据题目，以下哪个词组是“高频”的同义词？A. 常见B. 稀有C. 偶尔D. 罕见答案：A3. 在数学中，如果一个数的平方等于它本身，那么这个数可以是：A. 1B. 0C. -1D. 所有选项答案：D4. 以下哪个选项是正确的化学方程式配平？A. 2H2 + O2 → 2H2OB. H2 + O2 → H2OC. 2H2 + O2 → H2OD. H2 + O2 → 2H2O答案：A5. 在物理学中，下列哪个公式用于计算物体的动能？A. K = 1/2 mv^2B. K = mvC. K = m/sD. K = m * v^2答案：A二、填空题6. 根据题目，高频复习题通常指的是_________。

答案：在考试中经常出现的题目7. 一个物体从静止开始下落，其加速度为9.8m/s²，那么在第一秒内下落的距离是_________。

答案：4.9米8. 在化学中，一个化合物的化学式为H2O，表示该化合物由_________。

答案：两个氢原子和一个氧原子组成9. 根据题目，如果一个函数f(x)在x=a处连续，那么f(a)与_________。

答案：f(x)在x=a处的极限相等10. 在英语中，单词“frequent”的反义词是_________。

答案：infrequent三、简答题11. 请简述牛顿第二定律的内容。

答案：牛顿第二定律指出，物体的加速度与作用在物体上的净外力成正比，与物体的质量成反比。

数学表达式为F = ma，其中F是作用力，m是物体的质量，a是加速度。

12. 请解释什么是光的折射现象。

答案：光的折射现象是指光线在通过两种不同介质的交界面时，其传播方向发生改变的现象。

这是由于光在不同介质中的传播速度不同造成的。

高频电子线路复习例题第一章绪论一、填空题1．无线通信系统一般由信号源、__________、__________、___________、输出变换器五部分组成。

2．人耳能听到的声音的频率约在__________到__________的范围内。

（20HZ、20KHZ ）3．调制有_________、__________、_________三种方式。

（调幅、调频、调相）4．无线电波在空间的传播方式有________、_________、__________三种。

（地波、天波、直线波）二、简答或作图题1．画出无线通信调幅发射机原理框图，并说明各部分的作用，同时画出波形示意图和频谱示意图。

2. 画出超外差接收机方框图，并说明各部分的作用，同时画出波形示意图和频谱示意图。

3．在接收设备中，检波器的作用是什么？试画出检波器前后的信号波形。

4. 通信系统由哪些部分组成？各组成部分的作用是什么？答：通信系统由输入、输出变换器，发送、接收设备以及信道组成。

输入变换器将要传递的声音或图像消息变换为电信号（基带信号）；发送设备将基带信号经过调制等处理，并使其具有足够的发射功率，再送入信道实现信号的有效传输；信道是信号传输的通道；接收设备用来恢复原始基带信号；输出变换器将经过处理的基带信号重新恢复为原始的声音或图像。

第三章选频网络1、串联谐振和并联谐振的特征，以及失谐时表现出的特性。

如：LC回路并联谐振时，回路_阻抗___最大，且为纯__电阻__。

当所加信号频率高于并联谐振回路谐振频率时，回路失谐，此时，回路呈容性，电流超前电压。

2、由于信号源内阻或负载电阻的影响，将使谐振回路的品质因数Q ，选频特性 ，通频带 。

3、课后题 3.54、课后题 3.65、课后题 3.76、课后题 3.97、课后题 3.13 有一耦合回路如图，已知试求：1）回路参数L1、L2、C1、C2和M ； 2）图中a 、b 两端的等效谐振阻抗ZP ； 3）初级回路的等效品质因数Q1’； 4）回路的通频带BW ；解：由已知条件可知两个回路的参数是全同的，即L1=L2，C1=C2，Q1=Q2 ； 1）由 得：又由于发生临界耦合时 因此2）由于发生了临界耦合，所以R f1=R 1=20Ω 此时ab 两端的等效L 0ωρ=pF F LC C H H L L 15910159)102(11159102100062620216021=⨯⨯⨯====⨯===-πωμπωρ2120)(R R M =ωHH R R M μπω18.32020102116210=⨯⨯==)1000(22ρ1,20,¸1,121210201=Ω==Ω====ηρρR R K MHz f f谐振阻抗为纯阻，即3)初级回路的等效品质因数为4)初级回路本身的品质因数为因此可得出通频带为 ：8.图2-18所示电路为一等效电路，其中L =0.8uH,Q 0=100,C =5pF,C 1 =20pF,C 2=20pF,R =10k Ω,R L =5k Ω，试计算回路的谐振频率、谐振电阻。

七年级数学下册不等式与不等式组高频考点例题解析单选题1、为了落实精准扶贫政策，某单位针对某山区贫困村的实际情况，特向该村提供优质种羊若干只．在准备配发的过程中发现：公羊刚好每户1只；若每户发放母羊5只，则多出17只母羊，若每户发放母羊7只，则有一户可分得母羊但不足3只．这批种羊共（ ）只．A ．55B ．72C ．83D ．89答案：C解析：设该村共有x 户，则母羊共有（5x+17）只，根据“每户发放母羊7只时有一户可分得母羊但不足3只”列出关于x 的不等式组，解之求得整数x 的值，再进一步计算可得．设该村共有x 户，则母羊共有(5x +17)只，由题意知，{5x +17−7(x −1)>05x +17−7(x −1)<3解得：212<x <12，∵x 为整数，∴x =11，则这批种羊共有11+5×11+17=83（只），故选C ．小提示：本题主要考查一元一次不等式组的应用，解题的关键是理解题意找到题目蕴含的不等关系，并据此得出不等式组．2、下列说法中错误的是（ ）A．若a<b，则a+1<b+1B．若−2a>−2b，则a<bC．若a<b，则ac<bc D．若a(c2+1)<b(c2+1)，则a<b答案：C解析：根据不等式的性质进行分析判断．解：A、若a<b，则a+1<b+1，故选项正确，不合题意；B、若−2a>−2b，则a<b，故选项正确，不合题意；C、若a<b，若c=0，则ac=bc，故选项错误，符合题意；D、若a(c2+1)<b(c2+1)，则a<b，故选项正确，不合题意；故选C．小提示：本题考查了不等式的性质．解题的关键是掌握不等式的性质：①不等式的两边同时加上（或减去）同一个数或同一个含有字母的式子，不等号的方向不变；②不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变；③不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变．3、已知4＜m＜5，则关于x的不等式组{x−m<04−2x<0的整数解共有（）A．1个B．2个C．3个D．4个答案：B解析：先求解不等式组得到关于m的不等式解集，再根据m的取值范围即可判定整数解．不等式组{x−m<0①4−2x<0②由①得x＜m；由②得x ＞2；∵m 的取值范围是4＜m ＜5，∴不等式组{x −m <04−2x <0的整数解有：3，4两个． 故选B ．小提示：本题考查了一元一次不等式组的整数解，用到的知识点是一元一次不等式组的解法，m 的取值范围是本题的关键．4、若不等式组{2x −a <1x −2b >3的解 为−3<x <1，则(a +1)(b −1)值为（ ） A ．−6B ．7C ．−8D ．9答案：C解析：根据不等式的性质求出每个不等式的解集，根据找不等式组解集的规律找出不等式组的解集3+2b <x <a+12，根据不等式组的解集得出3+2b =−3，且a+12=1，求出a =1，b =−3，即可解答． 解：{2x −a <1①x −2b >3②， ∵解不等式①得：x <a+12，解不等式②得：x >3+2b ，∴不等式组的解集为3+2b <x <a+12，∵若不等式组{2x −a <1x −2b >3解为−3<x <1， ∴3+2b =−3，且a+12=1，解得：a =1，b =−3，∴(a +1)(b −1)=(1+1)×(−3−1)=−8，故选：C ．小提示：本题考查了不等式的性质，解一元一次不等式（组)，解一元一次方程等知识点，解此题的关键是根据不等式组解集得出关于a 和b 的方程，题目比较好，综合性比较强．5、若关于x 的不等式mx - n ＞0的解集是x <15，则关于x 的不等式(m +n)x >n −m 的解集是（ ） A ．x >−23B ．x <−23C ．x <23D ．x >23答案：B解析：先解不等式mx - n ＞0，根据解集x <15可判断m 、n 都是负数，且可得到m 、n 之间的数量关系，再解不等式(m +n)x >n −m 可求得解不等式：mx - n ＞0mx ＞n∵不等式的解集为：x <15∴m ＜0解得：x ＜n m ∴n m =15， ∴n ＜0，m =5n∴m +n ＜0解不等式：(m +n)x >n −mx ＜n−m m+n将m =5n 代入n−m m+n 得：n −m m +n =n −5n 5n +n =−4n 6n =−23∴x ＜−23故选：B小提示：本题考查解含有参数的不等式，解题关键在在系数化为1的过程中，若不等式两边同时乘除负数，则不等号需要变号.6、为了落实精准扶贫政策，某单位针对某山区贫困村的实际情况，特向该村提供优质种羊若干只．在准备配发的过程中发现：公羊刚好每户1只；若每户发放母羊5只，则多出17只母羊，若每户发放母羊7只，则有一户可分得母羊但不足3只．这批种羊共（ ）只．A ．55B ．72C ．83D ．89答案：C解析：设该村共有x 户，则母羊共有（5x+17）只，根据“每户发放母羊7只时有一户可分得母羊但不足3只”列出关于x 的不等式组，解之求得整数x 的值，再进一步计算可得．设该村共有x 户，则母羊共有(5x +17)只，由题意知，{5x +17−7(x −1)>05x +17−7(x −1)<3解得：212<x <12，∵x 为整数，∴x =11，则这批种羊共有11+5×11+17=83（只），故选C．小提示：本题主要考查一元一次不等式组的应用，解题的关键是理解题意找到题目蕴含的不等关系，并据此得出不等式组．7、不等式3x−2<4中，x可取的最大整数值是（）A．0B．1C．2D．3答案：B解析：首先解不等式，再从不等式的解集中找出适合条件的最大正整数即可．解：3x−2<4，3x<4+23x<6x<2，∴最大整数解是1．故选为：B．小提示：本题考查解一元一次不等式，一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键．8、若x=−3是关于x的方x=m+1的解，则关于y的不等式2(1−2y)≥−6+m的最大整数解为（）A．1B．2C．3D．4答案：C解析：把x=-3代入方程x=m+1，即可求得m的值，然后把m的值代入2（1-2x）≥-6+m求解即可．把x=−3代入方程x=m+1得：m+1=−3，解得：m=−4.则2(1−2x)⩾−6+m即2−4x⩾−10，解得：x⩽3.所以最大整数解为3，故选C.小提示：此题考查不等式的整数解，解题关键在于求得m的值. 填空题9、不等式组{x+1⩾12(x+3)−3>3x的解集是_____．答案：0≤x＜3解析：{x+1≥1①2(x+3)−3>3x②，解①得x≥0；解②得x<3；∴不等式组的解集是0≤x<3．故答案为0≤x<3．10、如图所示，点C位于点A、B之间（不与A、B重合），点C表示1﹣2x，则x的取值范围是_____．答案：−12<x<0解析：根据题意列出不等式组，求出解集即可确定出x的范围．解：根据题意得：1<1−2x<2，解得：−12<x<0，则x的范围是−12<x<0，所以答案是：−12<x<0.小提示：考查了解一元一次不等式组，以及数轴，熟练掌握运算法则是解本题的关键．11、不等式组{x+2>12−x≥−1的解集为__________.答案：−1<x≤3解析：分别求出不等式的解，再求解集即可.x＋2＞1，解得x＞﹣1，由2－x≥﹣1，解得x≤3，则不等式组的解集为﹣1＜x≤3.故答案是﹣1＜x≤3.小提示：本题主要考查不等式组的解法，熟练掌握解不等式组的方法是解答本题的关键.12、某校六年级的80名同学与2名老师共82人去公园春游，学校只准备了180瓶汽水．总务主任向老师交待，每人供应3瓶汽水(包括老师)，不足部分可到公园里购买，回校后报销．到了公园，商店贴有告示：每5个空瓶可换一瓶汽水．于是要求大家喝完汽水后空瓶由老师统一退瓶．那么用最佳的方法筹划，至少还要购买______瓶汽水回学校报销．答案：17解析：设还要购买x瓶，根据题意列出不等式，即可解出x的取值范围，再根据实际情况得出瓶数.设还要购买x 瓶，则180＋x ＋180+x 4≥82×3，解得x ≥16.8，∵x 必须是整数，∴x ≥17， ∴至少还要购买17瓶汽水回学校报销．故答案为17.小提示：此题主要考查不等式的应用，解题的关键是根据题意列出不等式.13、已知不等式组{x >1x <a −1无解，则a 的取值范围为__． 答案：a ⩽2解析：求出不等式组中每个不等式的解集，根据已知即可得出关于a 的不等式，即可得出答案．解：∵不等式组{x >1x <a −1无解， ∴a −1⩽1，解得：a ⩽2，所以答案是：a ⩽2．小提示：本题考查了一元一次不等式组的应用，解此题的关键是能得出关于a 的不等式，题目比较好，难度适中． 解答题14、求下列不等式组{3x >2(x −1)+3x+42≥x 的整数解． 答案：2，3，4．解析：首先解不等式组，然后确定不等式组的解集中的整数解即可．解：{3x >2(x −1)+3①x+42≥x② ， 解不等式①得：x >1，解不等式②得：x ≤4，所以不等式组的解集为1<x ≤4，所以不等式组的整数解为2，3，4．小提示：本题考查了求一元一次不等式组的整数解，熟练掌握不等式组的解法是解题关键．15、求不等式(2x −1)(x +3)>0的解集．解：根据“同号两数相乘，积为正”可得：①{2x −1>0x +3>0 或②{2x −1<0x +3<0解①得x >12，解②得x <−3．∴不等式的解集为x >1或x <−3．请你仿照上述方法求不等式(2x −3)(x +1)<0的解集．答案：−1<x <1.5．解析：根据“异号两数相乘，积为负”可得两个关于x 的不等式组，解之即可.解：根据“异号两数相乘，积为负”可得：①{2x −3>0x +1<0 或②{2x −3<0x +1>0解①得其无解，解②得−1<x <1.5．∴不等式的解集为−1<x <1.5小提示：本题考查了不等式组的解法，属于模仿题型，正确理解题意是解题的关键.11。

22.2.3 利用边角关系判定两三角形相似
课后作业：方案（B）
一.
完成教材P80 T1-T2
1.（1）在△ABC中，∠A=48°，AB=1.5cm,AC=2cm;在△DEF中，
∠E=48°,DE=2.8cm.EF=2.1cm，问这两个三角形相似吗？为什么？
（2）在△ABC中，∠A=120°，AB=7cm,AC=14cm;在△DEF中，
∠D=120°,DE=3cm.DF=6cm，问这两个三角形相似吗？为什么？
2.在Rt△ABC中，两直角边分别为3cm,4cm. 在Rt△AˊBˊCˊ中,斜边为25cm,一条直
角边15cm.问这两个直角三角形相似吗？为什么？
二.补充: 部分题目来源于《点拨》
8．如图，在平面直角坐标系中，A点坐标为(8，0)，B点坐标为(0，6)，C是线段AB的中点．请问在x轴上是否存在一点P，使得以P，A，C为顶点的三角形与
△AOB相似？若存在，求出P点坐标；若不存在，请说明理由．
9.如图，D为△ABC内一点，连接BD，AD，以BC为一边在△ABC外作△BCE，使△BCE
∽△BAD.
求证：△DBE∽△ABC.
10．〈江苏宿迁〉如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝8，AD ＝3，BC＝4，点P为AB边上一动点．若△PAD与△PBC是相似三角形，则满足条件的点P的个数是( )
A．1 B．2
C．3 D．4
答案
一、
教材。