小学二年级奥数：数数图形

一、计算题。

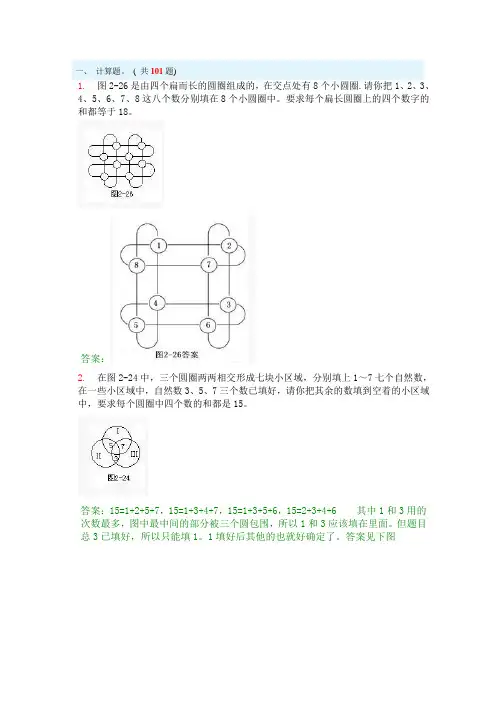
( 共101题)1.图2-26是由四个扁而长的圆圈组成的，在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。

要求每个扁长圆圈上的四个数字的和都等于18。

答案：2.在图2-24中，三个圆圈两两相交形成七块小区域，分别填上1～7七个自然数，在一些小区域中，自然数3、5、7三个数已填好，请你把其余的数填到空着的小区域中，要求每个圆圈中四个数的和都是15。

答案：15=1+2+5+7，15=1+3+4+7，15=1+3+5+6，15=2+3+4+6 其中1和3用的次数最多，图中最中间的部分被三个圆包围，所以1和3应该填在里面。

但题目总3已填好，所以只能填1。

1填好后其他的也就好确定了。

答案见下图3.图2-23中有三个大圆，在大圆的交点上有六个小圆圈。

请你把1、2、3、4、5、6六个数分别填在六个小圆圈里，要求每个大圆上的四个小圆圈中的数之和都是14。

答案：案把14拆成4个自然数的和，如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。

先把一个数填入，然后试一下确定其他数的位置。

答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表，使每一横行、竖行、斜行的三个数相加的和都相等。

答案：案九宫格填九数的方法，确定中间是10最关键了，然后我们对这些数加和除以3，就有了相等的和应该是30，图形如下(有很多种，但是中间那个肯定是10)5.仔细观察下面的图形，找出变化规律，猜猜在第3组的右框空白格内填一个什么样的图?答案：6.请看下图，共有多少个正方形?答案：30 个正方形。

小结小方格16 个，4 个小方格为一个正方形共 9 个，9 个小方格为一个正方形共 4 个，最大的(16 个小方格)是 1 个。

16+9+4+1=30(个)共计 30 个正方形。

7.仔细观察这些图案可以发现，他们是按照下面这5个图案为一组，循环往复排列的，请问第52个图形是什么?答案：8.把上面一排的立体图形剪开，可以剪成下面哪种图形的样子?动手试一试。

一、计算题。

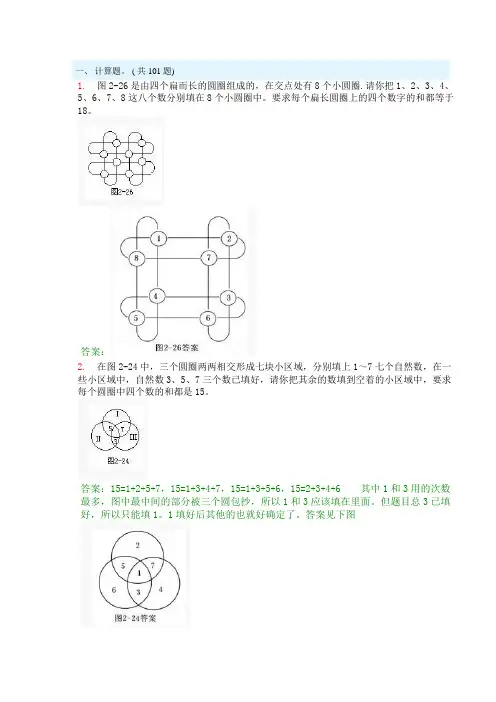
( 共101题)1.图2-26是由四个扁而长的圆圈组成的，在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。

要求每个扁长圆圈上的四个数字的和都等于18。

答案：2.在图2-24中，三个圆圈两两相交形成七块小区域，分别填上1～7七个自然数，在一些小区域中，自然数3、5、7三个数已填好，请你把其余的数填到空着的小区域中，要求每个圆圈中四个数的和都是15。

答案：15=1+2+5+7，15=1+3+4+7，15=1+3+5+6，15=2+3+4+6 其中1和3用的次数最多，图中最中间的部分被三个圆包围，所以1和3应该填在里面。

但题目总3已填好，所以只能填1。

1填好后其他的也就好确定了。

答案见下图3.图2-23中有三个大圆，在大圆的交点上有六个小圆圈。

请你把1、2、3、4、5、6六个数分别填在六个小圆圈里，要求每个大圆上的四个小圆圈中的数之和都是14。

答案：案把14拆成4个自然数的和，如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。

先把一个数填入，然后试一下确定其他数的位置。

答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表，使每一横行、竖行、斜行的三个数相加的和都相等。

答案：案九宫格填九数的方法，确定中间是10最关键了，然后我们对这些数加和除以3，就有了相等的和应该是30，图形如下(有很多种，但是中间那个肯定是10)5.仔细观察下面的图形，找出变化规律，猜猜在第3组的右框空白格内填一个什么样的图?答案：6.请看下图，共有多少个正方形?答案：30 个正方形。

小结小方格16 个，4 个小方格为一个正方形共 9 个，9 个小方格为一个正方形共 4 个，最大的(16 个小方格)是 1 个。

16+9+4+1=30(个)共计 30 个正方形。

7.仔细观察这些图案可以发现，他们是按照下面这5个图案为一组，循环往复排列的，请问第52个图形是什么?答案：8.把上面一排的立体图形剪开，可以剪成下面哪种图形的样子?动手试一试。

一、计算题。

( 共101题)1.图2-26是由四个扁而长的圆圈组成的，在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。

要求每个扁长圆圈上的四个数字的和都等于18。

答案：2.在图2-24中，三个圆圈两两相交形成七块小区域，分别填上1～7七个自然数，在一些小区域中，自然数3、5、7三个数已填好，请你把其余的数填到空着的小区域中，要求每个圆圈中四个数的和都是15。

答案：15=1+2+5+7，15=1+3+4+7，15=1+3+5+6，15=2+3+4+6 其中1和3用的次数最多，图中最中间的部分被三个圆包抄，所以1和3应该填在里面。

但题目总3已填好，所以只能填1。

1填好后其他的也就好确定了。

答案见下图3.图2-23中有三个大圆，在大圆的交点上有六个小圆圈。

请你把1、2、3、4、5、6六个数分别填在六个小圆圈里，要求每个大圆上的四个小圆圈中的数之和都是14。

答案：案把14拆成4个自然数的和，如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。

先把一个数填入，然后试一下确定其他数的位置。

答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表，使每一横行、竖行、斜行的三个数相加的和都相等。

答案：案九宫格填九数的方法，确定中间是10最关键了，然后我们对这些数加和除以3，就有了相等的和应该是30，图形如下(有很多种，但是中间那个肯定是10)5.仔细观察下面的图形，找出变更规律，猜猜在第3组的右框空白格内填一个什么样的图?答案：6.请看下图，共有多少个正方形?答案：30 个正方形。

小结小方格16 个，4 个小方格为一个正方形共 9 个，9 个小方格为一个正方形共4 个，最大的(16 个小方格)是 1 个。

16+9+4+1=30(个)共计 30 个正方形。

7.仔细观察这些图案可以发现，他们是依照下面这5个图案为一组，循环往复排列的，请问第52个图形是什么?答案：8.把上面一排的立体图形剪开，可以剪成下面哪种图形的样子?动手试一试。

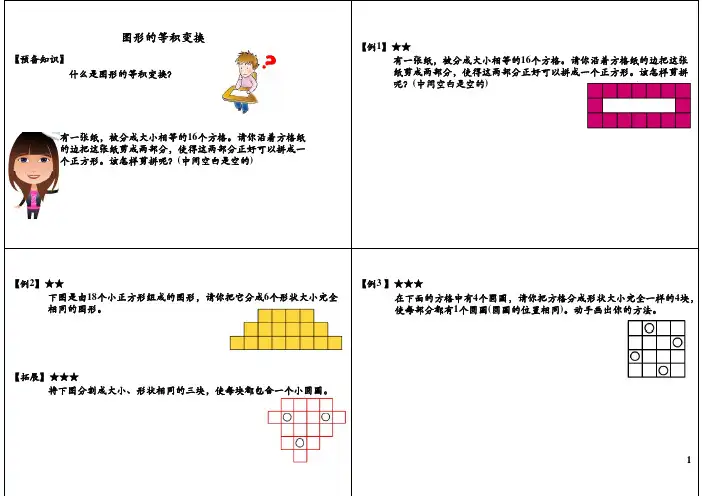
图形的等积变换
【预备知识】
什么是图形的等积变换？有一张纸被分成大小相等的个方格请你沿着方格纸有一张纸，被分成大小相等的16个方格。

请你沿着方格纸的边把这张纸剪成两部分，使得这两部分正好可以拼成一个正方形。

该怎样剪拼呢？中间空白是空的个形怎样剪拼(中间)
有张被成相等请着张有一张纸，被分成大小相等的16个方格。

请你沿着方格纸的边把这张纸剪成两部分，使得这两部分正好可以拼成一个正方形。

该怎样剪拼呢？(中间空白是空的)下图是由18个小正方形组成的图形，请你把它分成6个形状大小完全相同的图形。

将下图分割成大小、形状相同的三块，使每块都包含一个小圆圈。

在下面的方格中有4个圆圈，请你把方格分成形状大小完全一样的4块，使每部分都有1个圆圈(圆圈的位置相同)。

动手画出你的方法。

请把下面这个长方形沿方格线剪成形状、大小都相同的4块，使每一“”
块内都含有“中国加油”这四个字中的一个，该怎么剪？琳达家有三块连在一起的地板砖，如下图所示，她想把它分成大小、形状都相同的四块来垫桌腿，你有没有好办法？
请把下面的图形分成形状、大小都相同的4块，使每一块里面都有“史乐老师”4个字。

图形的剪拼方法一：
方法二：。

第十二讲图形竖式谜前续知识点：二年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲把里面的人物换成相应红字标明的人物．萱萱卡莉娅萱萱 卡莉娅卡莉娅卡莉娅，看我摆的小人，多漂亮啊！你摆的是什么啊？萱萱我不仅能摆出小人，还能摆出一头牛呢！厉害吧！哈哈~萱萱，竖式谜是一种有趣的数学问题．它的特点是给出运算式子，但式子中某些数字是用图形或者汉字来代表的，要求我们进行恰当的分析、判断和推理，从而确定这些图形或汉字所代表的数字．对于式子中的每一个位置，都可以从0至9这10个数字中选择一个，除非进行分析判断，否则想简单地直接通过试数的方法确定答案是极为费时费力的．因此，对于竖式谜必须以观察分析为基础，在此基础上才可以试数．这是竖式谜这类问题在思维顺序上的基本要求．【提示】从哪个数位入手呢？△＝（ ）☆＝（ ）△＝（ ）☆＝（ ） （1）（2）2 △ ＋△☆8 9☆ △ ＋△59 2下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？例题1（1） △＝（ ）☆＝（ ）（2）△＝（ ）☆＝（ ）△ 3 ＋ ☆ △88△ ☆ ＋ 3 △81下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？练习1【提示】相同的图形代表相同的数字哦！☆＝（ ）△＝（ ）☆＝（ ）（1）（2）☆ ☆ ＋ ☆6☆ △ ＋ △ △ 178下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？例题2☆＝（ ）△＝（ ） ☆＝（ ）（1）（2） ☆ ☆ ＋ ☆96☆ △ ＋ △ △ 1下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？练习2【提示】两个相同的数字相加得到的和是奇数还是偶数呢？△＝（ ） ☆＝（ ）△＝（ ） ☆＝（ ）（1）（2）☆ △ ＋ ☆ △86☆ △ ＋☆△7 4 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？ 例题3△＝（ ） ☆＝（ ）△＝（ ） ☆＝（ ）（1）（2）☆ △ ＋ ☆ △ 128☆ △ ＋ ☆ △92下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？练习3【提示】个位和十位上的两个数字相同．练习4 下面加法竖式中的“★”、“◎”各代表什么数字？请你写出两种答案．★＝（ ） ◎＝（ ）★＝（ ） ◎＝（ ）★ ◎ ＋ ◎ ★88下面加法竖式中的“★”、“◎”各代表什么数字？请你写出两种答案．例题4★＝（ ） ◎＝（ ）★＝（ ） ◎＝（ ）★ ◎ ＋◎ ★66【提示】一个两位数加一个两位数，最多能得到一个多大的三位数呢？【提示】两个数字相加有进位时，最多进几？“★”、“△”和“◎”分别代表三个不同的数字．请找出它们分别代表的数字，把这个竖式补充完整．1 ＋ ★ ★ ◎ △ △★＝（ ） ◎＝（ ） △＝（ ）例题6“★”、“△”和“◎”分别代表三个不同的数字．请找出它们分别代表的数字，把这个竖式补充完整．例题5★＝（ ） ◎＝（ ） △＝（ ）★ ◎ ＋ ◎ ◎ ★★△课堂内外小知识——数字诗数字诗，一般指诗中句句或多句含数字．诗歌创作的技巧很多,数字入诗乃技巧之一．巧用数字入诗，在古代诗歌中屡见不鲜，给人以新奇、独特之感，颇具回味．宋朝邵雍（康节）有一首五言数字诗《山村咏怀》，清新简单，朴实自然，堪称经典．诗云：一去二三里，烟村四五家；门前六七树，八九十枝花．明朝吴承恩有七言诗《明月夜静图》，是包含一到十的数字诗，比较受推崇．诗云：十里长亭无客走，九重天上现星辰．八河船只皆收港，七千州县尽关门．六宫五府回官宅，四海三江罢钓纶．两山楼头钟鼓响，一轮明月满乾坤．作业1. 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？2. 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？3. 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？4. 下面加法竖式中的“★”、“◎”各代表什么数字？请你写出两种答案．△＝（ ） ☆＝（ ）（1）△＝（ ） ☆＝（ ）（2）☆ △ ＋ ☆ △38☆ △ ＋ ☆ △ 164☆ △＋ △ △ 166△＝（ ） ☆＝（ ）（2）☆＝（ ）☆ ☆＋ ☆84（1）6 △ ＋ △ ☆97（1）△＝（ ） ☆＝（ ）（2） △＝（ ） ☆＝（ ）△ ☆＋ 2 △515. “★”、“△”和“◎”分别代表三个不同的数字．找出它们分别代表的数字，把竖式补充完整．★＝（ ） ◎＝（ ） △＝（ ）◎★ ＋ ◎ △ ★ △ ◎★ ◎ ＋ ◎ ★ 7 7★＝（ ） ◎＝（ ）★＝（ ） ◎＝（ ）第十二讲 图形竖式谜1. 例题1答案：（1）△＝5，☆＝3；（2）△＝4，☆＝7详解：加法竖式谜，从已知数字较多的数位入手．（1）从个位来看：△835=-=，则十位无进位，所以☆853=-=．所以△＝5，☆＝3．（2）从十位看：因为加法竖式中可能有进位，但是两个数字相加，最多进“1”，所以△835=-=或△8314=--=．当△＝5时，说明个位没有向十位进位“1”，从个位判断☆51+=，☆没有合适数字，所以△＝5不符合题意；那么当△＝4时，说明个位向十位进位“1”，从个位判断☆41+=，所以☆1147=-=．所以△＝4，☆＝7．2. 例题2答案：（1）☆＝8；（2）△＝5，☆＝4详解：在给出的图形较多的竖式中，从相同图形较多的数位入手．（1）从个位入手，☆+☆＝6，则☆为3或8．如果☆为3，十位就不符合，那么☆为8，向十位进1，819+=．所以☆＝8．（2）从个位入手，△+△＝0，则△为0或5．如果△为0，则十位不符合，那么△为5，向十位进1，可以得出☆10154=--=．所以△＝5，☆＝4．3. 例题3答案：（1）△＝4，☆＝6；（2）△＝6，☆＝4详解：当竖式数位上出现的相同图形个数一样多时，尽量按照竖式的计算顺序解题，即从个位入手．（1）两个相同的数字相加，得数是8，那么可以考虑这个数字是4或9．如果个位是4，那么没有进位，十位得数是2，可以考虑是1和6，而百位有进位，所以排除了十位是1的情况，那么十位是6；个位还可能是9，如果是9的话，就有进位，那么十位原来的两个数相加的和就是1或11，而十位的两个数是相同的，不可能出现奇数的情况，所以个位只能是4．所以△＝4，☆＝6．（2）看个位，两个相同的数相加，得数是2，那么可以考虑这个数是1和6，如果个位是1，那么没有进位，十位得数是9，两个相同的数相加的和是偶数，不存在两个相同的数相加为9，所以个位是6，向十位进1，所以十位上的两个相同的数相加就为8，那么这个数是4．所以△＝6，☆＝4．4. 例题4答案：★＝1，◎＝5；★＝2，◎＝4详解：个位和十位都是一样的数，和相同，可以确定加法竖式中没有进位．那么可以从比6小的数字举例子，当◎＝1时，那么★＝5；当◎＝2时，那么★＝4……，依次列举．注意当◎＝3时，那么★＝3，这个结果是不符合题意的，因为，“★”和“◎”代表的数字不相同．答案不唯一．5. 例题5答案：★＝1，◎＝9，△＝8详解：从首位分析，因为两个数字相加最多进1，百位有一个进位，那么可知★＝1，代入原竖式，如下图．由于十位有进位，所以可知：◎＝9，这时候得到△＝8．注意，竖式中有进位一定要把进位标上，以防忘记．6. 例题6答案：★＝9，◎＝1，△＝0详解：从首位分析，因为两个数字相加最多进1，百位有一个进位，那么可知◎＝1，代入原竖式，如下图．由于十位有进位，所以可知：★＝9，这时候从个位得到△＝0．注意，竖式中有进位一定要把进位标上，以防忘记．7. 练习1答案：（1）△＝6，☆＝3；（2）△＝7，☆＝1简答：加法竖式谜，从已知数字较多的数位入手．（1）从十位看：因为加法竖式中可能有进位，但是两个数字相加，最多进“1”，所以△826=-=或△8215=--=．当△＝6时，说明个位没有向十位进位“1”，从个位判断6+☆＝9，☆963=-=；那么当△＝5时，说明个位向十位进位“1”，从个位判断5+☆＝9，☆19514=-=，因为☆表示的是一个数字，所以△＝5不符合题意．所以△＝6，☆＝3．（2）从个位看：△52+=，则个位一定向十位进位“1”，所以△1257=-=；从十位判断：☆719++=，☆9711=--=．所以△＝7，☆＝1．8. 练习2答案：（1）☆＝5；（2）△＝9，☆＝7简答：在给出的图形较多的竖式中，从相同图形较多的数位入手．（1）从个位入手，☆+☆＝0，则☆为0或5．如果☆为0，十位就不符合，那么☆为5，向十位进1，516+=．所以☆＝5．（2）从个位入手，△+△＝8，则△为4或9．如果△为4，则十位不符合，那么△为9，向十位进1，可以得出☆17197=--=．所以△＝9，☆＝7．1 ＋★ ★1 △△ 11 ◎ ＋◎ ◎1 1△ 1 19.练习3答案：（1）△＝3，☆＝4；（2）△＝8，☆＝2简答：两个相同的数字相加，得数是6，那么可以考虑这个数字是3或8．如果个位是3，那么没有进位，十位得数是8，那么☆＝4；个位还可能是8，如果是9的话，就有进位，那么十位原来的两个数相加的和就是7，而十位的两个数是相同的，不可能出现奇数的情况，所以个位只能是4．所以△＝3，☆＝4．（2）看个位，两个相同的数相加，得数是4，那么可以考虑这个数是2或7，如果个位是2，那么没有进位，十位得数是7，两个相同的数相加的和是偶数，不存在两个相同的数相加为7，所以个位是7，向十位进1，所以十位上的两个相同的数相加就为6，那么这个数是3．所以△＝7，☆＝3．10.练习4答案：◎＝1，★＝7；◎＝2，★＝6简答：个位和十位都是一样的数，和相同，可以确定加法竖式中没有进位，且“★”和“◎”代表的数字不相同．那么可以从比8小的数字举例子，当◎＝1时，那么★＝7；当◎＝2时，那么★＝6……，依次列举．注意：当◎＝4时，那么★＝4，这个结果不符合题意．答案不唯一．11.作业1答案：（1）△＝3，☆＝4；（2）△＝2，☆＝9简答：从已知数多数位的入手．12.作业2答案：（1）☆＝7；（2）△＝8，☆＝7简答：观察竖式谜的特点，（1）中三个数都是一样的，那么由个位分析，只能是 2 或者7，通过排除法就可以得到正确答案；同理可以判断（2）．13.作业3答案：（1）△＝2，☆＝8；（2）△＝9，☆＝1简答：两个相同的数相加和为偶数，由此可知，（1）中没有进位，（2）中有进位．14.作业4答案：（1）★＝1，◎＝6；（2）★＝2，◎＝5简答：个位和十位都是一样的数，和相同，可以确定加法竖式中没有进位，且“★”和“◎”代表的数字不相同．那么可以从比7小的数字举例子，当◎＝1时，那么★＝6；当◎＝2时，那么★＝5……，依次列举．答案不唯一．15.作业5答案：★＝1，◎＝9，△＝8简答：首先确定★是1，然后从个位开始推断，个位△不可能是9，就说明没有进位，那么△只能是偶数，而且◎要比5大，通过尝试得出答案．。

第一讲：找规律数列中的规律：按照一定次序排列起来的一列数，叫做数列。

如自然数列：1、2、3、4……；双数列：2、4、6、8……。

我们研究数列，目的就是为了发现数列中数排列的规律，并依据这个规律来填写空缺的数。

按照一定的顺序排列的一列数，只要从连续的几个数中找到规律，那么就可以知道其余所有的数。

寻找数列的排列规律，除了从相邻两数的和、差考虑，有时还要从积、商考虑。

善于发现数列的规律是填数的关键。

例题1 在括号内填上合适的数。

（1）3，6，9，12，（），（）...（2）1，2，4，7，11，（），（）...（3）2，6，18，54，（），（）...举一反三：1，在括号里填数。

（1）2，4，6，8，10，（），（）...（2）1，2，5，10，17，（），（）...2，按规律填数。

（1）2，8，32，128，（），（）...（2）1，5，25，125，（），（）...例题2 先找出规律，再在括号里填上合适的数。

（1）15，2，12，2，9，2，（），（）（2）21，4，18，5，15，6，（），（）举一反三：先找规律再填数。

12，1，10，1，8，1，（），（）...2，1，4，1，6，1，（），（）；3，2，9，2，27，2，（），（）；18，3，15，4，12，5，（），（）；1，15，3，13，5，11，（），（）；例题3 先找出规律，再在括号里填上合适的数。

2，5，14，41，（）；252，124，60，28，（）；1，2，5，13，34，（）；1，4，9，16，25，36，（）；1，2，5，14，（），（）举一反三：按规律填数。

2，3，5，9，17，（）；2，4，10，28，82，（），（）；94，46，22，10，（），（）2，3，7，18，47，（），（）。

例题4 根据前面图形里的数的排列规律，填入适当的数。

举一反三：找出排列规律，在空缺处填上适当的数。

(1)131491611127149105(2)34984147216841236364122739(3)(1)141612141012895738427692887(2)5151272118927641632328161648(3)图形变化规律：【例 1】 观察这几个图形的变化规律，在横线上画出适当的图形．【例 2】 请找出下面哪个图形与其他图形不一样.【例 3】 观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

二年级奥数下册：第一讲机智与顿悟二年级奥数下册：第一讲机智与顿悟习题解答二年级奥数下册：第二讲数数与计数二年级奥数下册：第二讲数数与计数习题二年级奥数下册：第二讲数数与计数习题解答将8个小立方块组成如图2-5所示的“丁”字型，再将表面都涂成红色，然后就把小立方块分开，问：(1)3面被涂成红色的小立方块有多少个?(2)4面被涂成红色的小立方块有多少个?(3)5面被涂成红色的小立方块有多少个?【答案解析】如图2-6所示，看着图，想像涂色情况.当把整个表面都涂成红色后，只有那些“粘在一起”的面(又叫互相接触的面)，没有被涂色.每个小立方体都有6个面，减去没涂色的面数，就得涂色的面数.每个小立方体涂色面数都写在了它的上面，参看图2-6所示.(1)3面涂色的小立方体共有1个;(2)4面涂色的小立方体共有4个;(3)5面涂色的小立方体共有3个.例 1数一数，图 2－1 和图 2－2 中各有多少黑方块和白方块？解：仔细观察图 2－1，可发现黑方块和白方块同样多.因为每一行中有 4 个黑方块和 4 个白方块，共有 8 行，所以：黑方块是：4×832（个）白方块是：4×832（个）再仔细观察图 2－2，从上往下看：第一行白方块 5 个，黑方块4 个；第二行白方块 4 个，黑方块5 个；第三、五、七行同第一行，第四、六、八行同第二行；但最后的第九行是白方块 5 个，黑方块 4 个.可见白方块总数比黑方块总数多 1 个. 白方块总数：54545454541（个）黑方块总数：45454545440（个）再一种方法是：每一行的白方块和黑方块共 9 个. 共有 9 行，所以，白、黑方块的总数是：9×981（个）. 由于白方块比黑方块多 1 个，所以白方块是 41 个，黑方块是 40 个.例 2图 2－3 所示砖墙是由正六边形的特型砖砌成，中间有个“雪花”状的墙洞，问需要几块正六边形的砖（图 2－4）才能把它补好？解：仔细观察，并发挥想象力可得出答案，用七块正六边形的砖可把这个墙洞补好.如果动手画一画，就会看得更清楚了.例 3将 8 个小立方块组成如图 2－5 所示的“丁”字型，再将表面都涂成红色，然后就把小立方块分开，问：（1） 3 面被涂成红色的小立方块有多少个？（2）4 面被涂成红色的小立方块有多少个？（3）5 面被涂成红色的小立方块有多少个？解：如图 2－6 所示，看着图，想像涂色情况.当把整个表面都涂成红色后，只有那些“粘在一起”的面（又叫互相接触的面），没有被涂色.每个小立方体都有6 个面，减去没涂色的面数，就得涂色的面数.每个小立方体涂色面数都写在了它的上面，参看图 2－6 所示. （1）3 面涂色的小立方体共有 1 个；（2）4 面涂色的小立方体共有 4 个；（3）5 面涂色的小立方体共有 3 个.例 4如图 2－7 所示，一个大长方体的表面上都涂上红色，然后切成18 个小立方体（切线如图中虚线所示）.在这些切成的小立方体中，问：（1）1 面涂成红色的有几个？（2）2 面涂成红色的有几个？（3）3 面涂成红色的有几个？解：仔细观察图形，并发挥想像力，可知：（1）上下两层中间的 2 块只有一面涂色；（2）每层四边中间的 1 块有两面涂色，上下两层共 8 块；（3）每层四角的 4 块有三面涂色，上下两层共有 8 块.最后检验一下小立体总块数：28818（个）.习题1.如图 2－8 所示，数一数，需要多少块砖才能把坏了的墙补好？2.图 2－9 所示的墙洞，用 1 号和 2 号两种特型砖能补好吗？若能补好，共需几块？3.图 2－10 所示为一块地板，它是由 1 号、2 号和 3 号三种不同图案的瓷砖拼成.问这三种瓷砖各用了多少块？4.如图 2－11 所示，一个木制的正方体，棱长为 3 寸，它的六个面都被涂成了红色.如果沿着图中画出的线切成棱长为 1 寸的小正方体. 求：（1）3 面涂成红色的有多少块？（2）2 面涂成红色的有多少块？（3）1 面涂成红色的有多少块？（4）各面都没有涂色的有多少块？（5）切成的小正方体共有多少块？5.图 2－12 所示为棱长 4 寸的正方体木块，将它的表面全染成蓝色，然后锯成棱长为 1 寸的小正方体.问：（1）有 3 面被染成蓝色的多少块？（2）有 2 面被染成蓝色的多少块？（3）有 1 面被染成蓝色的多少块？（4）各面都没有被染色的多少块？（5）锯成的小正方体木块共有多少块？6.图 2－13 所示为一个由小正方体堆成的“塔”.如果把它的外表面（包括底面）全部涂成绿色，那么当把“塔”完全拆开时，3 面被涂成绿色的小正方体有多少块？7.图 2－14 中的小狗与小猫的身体的外形是用绳子分别围成的，你知道哪一条绳子长吗？（仔细观察，想办法比较出来）.习题解答1.解：用 10 块砖可把墙补好，可以从下往上一层一层地数（发挥想像力）：共12212210（块）. 如果用铅笔把砖画出来（注意把砖缝对好）就会十分清楚了，如图 2－15 所示.2.解：仔细观察，同时发挥想像力可知需 1 号砖 2 块、2 号砖 1 块，也就是共需（如图 2－16 所示） 123（块）.3.解：因为图形复杂，要特别仔细，最好是有次序地按行分类数，再进行统计：4.解：（1）3 面涂色的有 8 块：它们是最上层四个角上的 4 块和最下层四个角上的 4 块. （2）2 面涂色的有 12 块：它们是上、下两层每边中间的那块共8 块和中层四角的 4 块. （3）1 面涂色的有 6 块：它们是各面（共有 6 个面）中心的那块. （4）各面都没有涂色的有一块：它是正方体中心的那块. （5）共切成了3×3×327（块）. 或是如下计算： 8126127（块）.5.解：同上题（1）8 块；（2）24 块；（3）24 块；（4）8 块；（5）64 块.6.解：面被涂成绿色的小正方体共有 16 块，就是图 2—18 中有“点” 的那些块（注意最下层有 2 块看不见）.7.解：分类数一数可知，围成小猫的那条绳子比较长.因为小狗身体的外形是由32 条直线段和 6 条斜线段组成；小猫身体的外形是由 32 条直线段和 8 条斜线段组成.二年级奥数综合练习1、按规律填数。

第一讲“几和第几”例1 圈一圈，涂一涂。

把左边的5 朵圈起来。

从左起，把第5朵涂上颜色。

把右边的6个圈起来，从右数，把第5个涂上颜色。

例2 一共11个五角星，把中间的一个五角星涂上颜色，中间的五角星是第几个？一例一练：把中间的一个圆涂上颜色，它的前后都有（）个。

例3在第（），在第（）( )第2，（）第4。

例4小芳小阳小丽小琴小华1、共有（）个小朋友，2、从右数，小阳在第（），第3个是（）。

例5 报数游戏。

从1报到10，报2和5的同学拍手。

一例一练：从10报到1，报3和7的同学拍手。

例6 小朋友排队，从前数，小小是第4个，从后数，她是第3个，这一队共有几人？一例一练：一共有10个小朋友排队，小小的前面有3人，小小的后面有几人？练习题：1、一共有（）只动物。

从左数，排第（）。

排第（）。

2、一共有（）只。

把右边的7只圈起来。

从右边数起，把第7只涂上颜色。

3、一共有（）个。

从左起，涂色的是第（）。

4、水果一共有（）个。

从左边数起，把第5个涂上颜色。

5把右边的7个圈起来。

从右边起，把第7个涂上颜色。

6、涂色：从左边起，第一排涂4个，第二排第4个。

7、从左数，在第（ ）。

从右数，在第（ ）8、下图是8个队员正步向前走，穿黑衣服的组长排在第6个，教练员发令：向后转，穿红衣服的组长排在第?9、报数游戏： 看谁先抢到7。

（可以一个一个的报，也可以两个两个的报） 10、数学童话故事：数字兄弟。

第二讲 数一数（一）例1 数一数，下图中有几个正方形、几个等边三角形、几个圆？例2 数一数，下图中共有多少点？1+3+6+9+12=31共有31个点。

例3 数一数，下图中有几条线段？照下面的方法数：3+2+1=6（条）。

例4 数一数，下图中有几个锐角？照下面的方法数：3+2+1=6（个）。

习题1．数一数，下图中有几个锐角？几个直角？几个钝角？2．数一数，下图中有几个等边三角形？有几个等腰三角形？有几个直角三角形？有几个等腰直角三角形？3．数一数，下图中有几个正方形？有几个长方形？有几个平行四边形？几个四边形？4．数一数，下图中共有多少点？5．数一数，下图中共有几条线段？6．下图中共有10条线段，你能把它们都找出来吗?7．数一数，下图中有几个锐角？8．下图中共有10个角，你能把它们都找出来吗？第三讲数一数（二）数复杂的图形需要较强的观察能力，要细心，做到不重不漏。

第五讲数数游戏本节课主要是给学生介绍一些不规则图形的计数方法，比如跳棋孔有多少个，蜘蛛网上有多少个点等问题.把数数和生活联系起来，让学生在练习的过程中，能根据不同的情况，找到最简便的计数方法，这里也巧妙的巩固了前面所学的乘法，让学生进一步理解了乘法的意义.考考你小朋友们，请你数一数下面的图形里面有多少个.【教学思路】这两个题属于之前学习过的图形计数.课前可以做为思考题让学生来思考.第一个图中可以先横着数，再竖着数，合起来一共有12个.第二个图中第一个看不见的有4个，第二个看不见的有3个.猜一猜下图看不见的有几块?数一数，下面一共有多少个正方形？【教学思路】一共有4+9+5+4+1=23（个）正方形.小朋友们都是数数的小能手，在生活中有很多需要我们通过数数来解决的问题，数数的方法有很多，你会哪一种呢？今天这节课就让我们大显身手吧！基础篇猜谜语：一树五枝丫，不长叶和花，会写会画画.劳动都靠它.这是（）.一只手有( )手指：3个人共有多少个手指?【教学思路】人体有数字5的器官有手和脚，但脚不会拿笔画画，所以谜底是手.3个人共有6只手.所以3个人共有手指：5+5+5+5+5+5=30(个)，用乘法：5×6=30（个）或6×5=30（个）.在这里要引导学生用简便方法来计算.拓展练习还记得这首诗吗?请你数数，去掉标点后，有几个字?【答案】第一排有3个字，后面的三排每排有5个字，我们这样数比较简单：5×3+3=18（个）或3×5+3=18（个）.还可以把第一排也看成5个，然后把多数的两个减掉.5×4-2=18（个）或4×5-2=18（个）像下图这样摆出一个长方形，一共用了多少根小棒?摆出一个正方形，一共用了多少根小棒？【教学思路】摆出一个长方形，一共用了多少根小棒?可以这样数横着的小棒有8×2=16（根）竖着的小棒一共有9根，合起来一共有16+9=25（根）.摆出一个正方形，一共用了多少根小棒？可以这样数，横着的小棒一共有3×4=12（根），竖着的小棒一共有3×4=12（根），合起来一共有12+12=24（根）拓展练习一黑一白两海龟，全用三角形来拼.小朋友们数一数，两只海龟共用几个三角形？【答案】我们先思考一个小海龟用了几个三角形，可以拿白色的海龟来观察.方法一：把中间的正方形分成三角形然后来数一数.分层数：第一层有6个小三角形；第二层有10个小三角形；第三层有2个小三角形.一共有6+10+2=18(个)小三角形.方法二：数一数，这个小海龟是由6个正方形和6个三角形组成.一个正方形可以分成两个三角形，那么6个正方形就是12个小三角形，一共有多少个小三角形可以列式：6×2+6=18（个）一只小海龟用了18个小三角形，两只小海龟就用了18+18=36（个）小三角形.小圆圈拼图形，数一数有几个？【教学思路】在这个正六边形的图形中，一共有几个圆圈呢？方法一：最基本的方法，可以一层一层的数，5+6+7+8+9+8+7+6+5=61（个）.方法二：发现规律，分组数.第一排和最后一排都是5个，共5×2=10个；第二排和倒数第二排都是6个，共6×2=12个；第三排和倒数第三排都是7个，共7×2=14个；第四排和倒数第四排都是8个，共8×2=16个，只有第五排是9个.可以用简便方法来计算：5×2+6×2+7×2+8×2+9=10+12+14+16+9=61（个）.方法三：把较大的图形分成若干个小图形.如下图：可以把这个图形分成相同的6个三角形来计算.一个三角形里有10个，6个三角形就是60个.再加上中间的一个就是61个.列式6×10+1=61（个）小朋友们都玩过跳棋吧！你知道跳棋棋盘上有多少个圆洞吗?数一数.【教学思路】首先老师要对跳棋这种游戏做一下介绍.这道题是上一题的拓展，跳棋棋盘上的圆洞排列是有一定规律的，如果学生一个一个数容易数错，我们应该找规律，把这个不规则的图形分成若干个小块来数.方法一：如右图来分割，分成外面6个一样的三角形和里面一个正六边形，里面正六边形在上一题中我们已经数过了是61个，外面每个三角形有10个洞，6个三角形一共有60个洞.合起来一共是61+60=121（个）方法二：如右图来分割，六个平行四边形一共有16×6=96（个）合起来一共是96+4×6+1=121（个）方法三：如右图，分成6个平行四边形，把它们的个数加起来.25+20+20+20+20+16=121（个）小新用圆片摆了“中国”两个字，你知道一共用了多少个“○”?【答案】每个字我们都可以分组来数：“中”一共有：7×2+11+11+12=48（个）或13+13++5×2+12=48（个）“国”一共有：11+11+10+10+8×3+7=73（（个）或12+12+9×2+8×3+7=73（个）一共用了48+73=121（个）.在这个题中有几个相同的数，如果这个数字超过了10，我们就直接加，不用乘法计算.小朋友们，你能用圆片摆出“北京”两个字吗？回家试一试，然后数一数一共用了多少个圆片.【教学思路】老师在头一天布置学生回家自己摆，然后贴在白纸上.第二天上课时在班上交流，选择部分较好的作品，让大家一起数一数.猜谜语，再填数.小小飞天王，吐丝织罗网，摆开八卦阵，蚊蝇美美尝.这是（）.①蜘蛛网中心有一个点.织到第一层一共有（）个点.织到第二层一共有（）个点……现在这个蜘蛛网上一共有（）个点？②如果蜘蛛网织到第八层，一共有（）个点？【教学思路】这道题要引导学生找蜘蛛网的规律.①蜘蛛网中心有一个点，再数第一层有8个点，算织到第一层一共有多少个点，就还要算上原来中心的一个点，一共是8+1=9（个）.如下图1.再数一数，第二层也有八个点，那么织到第二层一共就有8×2+1=17（个），如下图2.图1 图2这个蜘蛛网上一共有多少个点呢？方法一：继续往下数我们发现第3层有8个点，第4层有8个点，第5层也有8个点.于是我们发现每层点的个数是不变的，只是两个点之间的距离越来越大.一共有5层，每层都有8个，就是40个点，再加上中间的一个，一共就是41个点.列式：一共有8×5+1=41（个）方法二：我们发现每个点都是在一条直线上.我们可以先计算每条直线上的点，再用乘法求总数.列式：5×8+1=41（个）.②如果蜘蛛网织到第八层，一共有多少个点呢？因为每层都是8个点，8层就是64个点，再加上正中心的一个点，蜘蛛网织到第八层一共就有65个点.列式：8×8+1=65（个）附加题（老师可根据自己的课堂进度灵活处理讲义内容，附加题仅供老师参考使用.）你认识象棋的棋盘吗？整个象棋的大小一共有多少个方格子？【教学思路】数一数，每层有8个方格，整个有9层（算大小还要包括中间的河界部分），这样这个象棋的大小就有8×9=72（个）方格子.数数看，下边这张床是由多少个小正方体组成的?【教学思路】我们可以一部分一部分的来数，先数床头部分，一共有4×7=28（个）；再数床身中间部分有4×8+4×8=64（个）；最后数床尾有4×3=12（个）.合起来这张床一共有28+64+12=104（个）小正方体.练习五1.数一数.【答案】（1）5×6=30（个）或6×5=30（个）（2）5×7=35（个）或7×5=35（个）2.下图一共有多少个小方块？有几个看不见？【答案】一共有10个小方块，有4个看不见.3. 数一数，下图有多少个△?【答案】一共有15+15+8=38（个）.4.下面的长方形是用多少根小棒摆成的？【答案】横着数一共有8×4=32（根），竖着数一共有3×9=27（根），一共有32+27=59（根）.5. 数一数，一共有多少个正方形?【答案】一共有6个正方形.小敏很喜欢画.她家的墙上挂着许多画，其中有一幅是“带有数字的小狗”.狗尾巴上的数是几呢？我们分析下面一只狗所带的数字，便可以得到启发.噢！原来狗的前腿圈中的两个数相加正好等于后腿与尾巴圈中的三个数字之和.小朋友，现在你该知道狗尾巴上的数是几了吧！。

二年级奥数：图形七十二变前铺知识一、图形的剪【例题】你能将下面的图形，剪成形状、大小相同的4块么？看谁的方法多！【解析】总共16个小方格，分成一样的4块，每块就是16÷4=4（个）小方格。

4个小方格可组成的形状有以下5种：（1）（2）（3）（4）（5）法1 法2 法3 法4 法5二、图形的拼【例题】从下面四个图形中，选两个可以拼成长方形的图形。

【解析】（1）、（3）三、图形的剪拼找目标【例题】你能把下面的图形剪一刀，然后再拼成正方形么？试试看吧！【解析】先在原图上，画出我们的目标图形正方形，如下图（1），然后看缺的部分和多余的部分，如果缺的和多的正好一样，那就成功了，如下图（2）。

变成（1）（2）四、图形的拼组【例题】请用4个一样大小的等边三角形拼成一个大的等边三角形。

【解析】图形能分就能拼，能拼就能分。

用4个一样大小的等边三角形能拼成一个大的等边三角形，那么，一个大的等边三角形就能分成4个小的一样大小的等边三角形。

那么，我们就可以选择把等边三角形分成4个小等边三角形，如下图所示。

图形七十二变知识点总结二、巧拼图形1、找目标：先边角位置2、按顺序分层三、图形剪拼原图上找目标四、图形分割1、先定大小：每份数=总数÷份数2、再定形状：先从边角入手例题精讲【例2】下面有5组图形，每个各有5个小正方形，请把这5个图形拼成一个大正方形，可以怎样拼？134 5解析：这个题目最好的办法就是动手摆一摆、试一试，当然它也有一定的方法与技巧。

在用方块拼图形时，我们要从边入手。

在这道题中，就可从一边方块数最多的5号入手。

再分层解决，观察出3号能直接塞进去。

下图是拼好后的图形，参考拼图顺序为5号→3号→4号→1号→2号（为方便观察，现将不同编号的图形绘制成不同颜色）【例4】有一张纸，被分成了大小相等的16个方格。

请你沿着方格纸的线把这张纸剪成形状、大小都相同的两部分，使得这两部分正好可以拼成一个正方形。

154第五讲 认识图形(数图形)ʌ知识概述ɔ我们已经认识了点㊁线段㊁角㊁三角形㊁正方形㊁长方形等各种图形㊂我们要学会数图形,会数有多少个点,多少条线段,多少个角,多少个三角形,多少个正方形等㊂数图形要根据图形的特点,按照一定的顺序有条理地来数,做到不重复㊁不遗漏,又快又准㊂数图形要有一定的方法,分类数是一种重要的方法㊂如:数数下图中有多少个长方形:分类数就是先数基本的长方形(中间没有别的线段)有2个,再数由2个基本长方形组成的长方形有1个,所以,这个图形中一共有3(即2+1)个长方形㊂这样,既有顺序又分类来数,就能做到不重复不遗漏㊂例题精学例1 图(1)中有多少个 ㊃ ?图(2)中有多少条线段?(1) (2)ʌ思路点拨ɔ 图(1)要求数多少个点,方法是从上到下,每排分别有1个㊁2个㊁3个㊁4个㊁5个 ㊃ ,所以一共有:1+2+3+4+5=15(个)也可以从左侧看向右侧,斜行分别有5个㊁4个㊁3个㊁2个㊁1个 ㊃ ,所以一共有:5+4+3+2+1=15(个)155图(2)要求数线段,方法是先数基本线段有3条(A B ㊁B C ㊁C D ),两条基本线段组成的线段有2条(A C ㊁B D ),三条基本线段组成的线段有1条(A D ),所以图中共有线段的条数是:3+2+1=6(条)数图(2)中线段的条数,也可以看端点,每两个端点组成一条线段㊂以A 为一个端点有3条,即A B ㊁A C ㊁A D ;以B 为端点的线段有B C ㊁B D (B A 已统计过),以C 为端点的线段有C D (C B ㊁C A 已统计过),所以图(2)中共有线段的条数是:3+2+1=6(条)或3ˑ4ː2=6(条)同步精练1.图(1)中有多少个 ㊃ ?图(2)中有多少条线段?(1) (2)2.数一数,下图中一共有多少条线段?3.下面给出5个点,每两点之间画一条线段,共有多少条线段?156例2 数一数,图中共有多少个角?(每个角都小于90度)ʌ思路点拨ɔ 数线段的方法和数角的方法很相似㊂我们分类来数:图中基本角有4个(øA O B ㊁øB O C ㊁øC O D ㊁øD O E ),两个基本角组成的角有3个(øA O C ㊁øB O D ㊁øC O E ),三个基本角组成的角有2个(øA O D ㊁øB O E ),四个基本角组成的角有1个(øA O E ),所以上图中共有的角的个数是:4+3+2+1=10(个)㊂同步精练1.下图中一共有多少个角?2.下图中一共有多少个三角形?3.下图中一共有多少个直角?例3图(1)中有多少个长方形?图(2)中有多少个正方形? (1)(2)ʌ思路点拨ɔ把图(1)看成两层,每层中3+2+1=6(个)长方形,两层共有6ˑ2=12(个)长方形;两层合起来,看作一大层,也有6个较大的长方形,因此图(1)中共有长方形:(3+2+1)ˑ3=18(个)㊂把图(2)分类来数,最小的正方形有13个,四个小正方形组成的样的正方形有6个,九个小正方形组成的样的正方形有1个,所以图(2)中共有正方形:13+6+1=20(个)㊂同步精练1.图(1)中有()个长方形,图(2)中有()个正方形㊂图(1)图(2)157158 2.下图中共有( )个长方形㊂3.下图中共有()个正方形㊂例4下图是由多个小方块堆成的图形,数一数,图中共有多少个小方块?ʌ思路点拨ɔ数方块要有条理,按照一定的顺序来数,看见的要数,看不见的也要数㊂方法一:从上到下分别有1个㊁3个㊁8个,所以共有:1+3+8=12(个)方法二:从左到右分别有2个㊁3个㊁4个㊁3个,所以共有:2+3+4+3=12(个)方法三:从前到后,分别有4个㊁8个,所以共有:4+8=12(个)方法四:看见的有9个,看不见的有3个,所以共有:9+3=12(个)同步精练1.数一数,下图中共有()个小方块㊂2.数一数,下图中共有()个小方块㊂3.数一数,下图中共有()盒牛奶㊂159160练习卷数一数,填一填㊂1.数一数,下图中共有()个ʻ㊂2.下面的五角星中共有()条线段㊂3.下图中共有()个长方形㊂4.下图中含有ʀ的正方形共有()个㊂5.一个正方形有4个直角,剪去一个角,还有()个直角㊂1616.下图中共有( )个角,( )个三角形㊂7.数一数,下图中有( )个长方形,( )个正方形,( )个三角形,( )个圆㊂8.数一数,下图中共有( )个三角形㊂9.数一数,下图是由( )个小方块堆成的㊂10.下图中有( )个三角形,( )个正方形㊂2.3.4.第二行最后一格画:;第三行最后一格画:5.6.二㊁1.第7块选(2)号;第8块选(1)号㊂2.第7格选(3)号;第8格选(4)号㊂3.在最后6个黑珠子后面空下7个白珠,接下去把8个ʻ涂黑㊂4.第五讲认识图形(数图形)例1(1)1+2+3+4+5=15(个)(2)3+2+1=6(条)或3ˑ4ː2=6(条)[同步精练]1.(1)有5ˑ5=25(个)(2)有4+3+2+1=10(条)线段㊂2.有(2+1)ˑ2+2=8(条)线段㊂2973.共有(3+2+1)ˑ5+5=35(条)线段㊂例2共有角4+3+2+1=10(个)[同步精练]1.共有3+2+1=6(个)角㊂2.共有5+4+3+2+1=15(个)三角形㊂3.共有10个直角㊂例3(1)有长方形:(3+2+1)ˑ3=18(个)㊂(2)有正方形:13+6+1=20(个)㊂[同步精练]1.2160(提示:(1)共有6+5+4+3+2+1=21(个)长方形㊂(2)共有7ˑ4+3ˑ6+2ˑ5+1ˑ4=60(个)正方形)2.33(提示:共有(4+3+2+1)ˑ3+3=33(个)长方形)3.91(提示:共有6ˑ6+5ˑ5+4ˑ4+3ˑ3+2ˑ2+1=91(个)正方形)例412个[同步精练]1.11(提示:3+3+5=11(个)小方块)2.30(提示:共有1+4+9+16=30(个)小方块)3.9(提示:共有3+4+2=9(盒)牛奶)练习卷1.25(提示:共有5ˑ5=25(个)ʻ)2.30(提示:共有(3+2+1)ˑ5=30(条)线段)2983.36(提示:共有(3+2+1)ˑ(3+2+1)=36(个)长方形)4.45.3㊁2或1(提示:)6.126(提示:有3+2+1+6=12(个)角,有3+2+1=6(个)三角形)7.41458.24(提示:有(4+3+2+1)ˑ2+4=24(个)三角形)9.22(提示:有4+6ˑ3=22(个)小方块)10.4010(提示:有16+16+4+4=40(个)三角形,10个正方形)第六讲有余数的除法(认识余数)例1(1)由2ˑѲ+1=ә7,得Ѳ=8,ә=1㊂(2)由7ˑ8+Ѳ=ә2,得Ѳ=6,ә=6㊂[同步精练]1.(1)ә=9,Ѳ=7㊂(2)ә=6,Ѳ=5㊂2.(1)余数是8,被除数是89,җ=8㊂(2)余数是1,被除数是49,җ=9㊂3.这样的被除数可能有5个,是47,38,29,20,11㊂例2解:根据Aː7=B 3(个),假设B是1,2,3,4,5,6时,得A=10,17,24,31,38,45㊂答:这堆苹果有10个或17个或24个或31个299。

(完整版)二年级奥数数数图形专题练习编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)二年级奥数数数图形专题练习）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)二年级奥数数数图形专题练习的全部内容。

（完整版）二年级奥数数数图形专题练习编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方，但是我们任然希望 (完整版)二年级奥数数数图形专题练习这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈(完整版）二年级奥数数数图形专题练习> 这篇文档的全部内容。

二年级奥数试听课数数图形专题简析：我们已经认识了线段、角、三角形、长方形等基本图形，当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。

要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律,才能获得正确的结果。

要准确、迅速地计数图形必须注意以下几点：1，弄清被数图形的特征和变化规律.2，要按一定的顺序数，做到不重复，不遗漏。

例1:数出下面图中有多少条线段.分析与解答：要正确解答这类问题，需要我们按照一定的顺序来数，做到不重复,不遗漏。

从图中可以看出,从A点出发的不同线段有3条:AB、AC、AD；从B点出发的不同线段有2条：BC、BD；从C点出发的不同线段有1条:CD。

第十一讲数数块数（必做与选做）1.下面图形有（）块小方块。

A. 5B. 6C. 7D. 8解析：要正确数出图中有多少块小方块，可以分层数，将图形分成上、下两层。

上面一层有1块，下面一层有6块（其中看得见的有5块，被挡住的有1块），上下两层小方块的块数相加，1+6=7（块），就是整个图形的小方块数。

2.下面图形有（）块小方块。

A. 9B. 10C. 14D. 16解析：要正确数出图中有多少块小方块，可以分层数，将图形分成上、下两层。

上面一层有7块，下面一层有9块，上下两层小方块的块数相加，7+9=16（块），就是整个图形小方块数。

3. 下面图形有（）块小方块。

A. 5B. 6C. 7D. 8解析：要正确数出图中有多少块小方块，可以分层数，将图形分成上、中、下三层。

上面一层有1块，中间一层有3块（其中看得见的有2块，被挡住的有1块），下面一层块数和中间一层块数相同。

上、中、下3层小方块的块数相加，1+3+3=7（块），就是整个图形的小方块数。

4. 下面图形有（）块小方块。

A. 11B. 10C. 9D. 8解析：把图形分为上、中、下三层，认真分析三层小方块数量的关系。

从图中可知，上层有1块小方块；中层比上层多3块，有1+3=4（块）；下层比中层多2块，有2+4=6（块）。

上、中、下三层的块数加起来为1+4+6=11（块），整个图形有11块小方块。

5. 下面图形有（）块小方块。

A. 9B. 12C. 15D. 18解析：把图形分为上、中、下三层，认真分析三层小方块数量的关系。

从图中可知，上层有3块小方块；中层比上层多2块，有2+3=5（块）；下层比中层多5块，有5+5=10（块）。

上、中、下三层的块数加起来为3+5+10=18（块），整个图形有18块小方块。

6. 下面图形有（）块小方块。

A. 9B. 15C. 18D. 21解析：把图形分为上、中、下三层，认真分析三层小方块数量的关系。

从图中可知，上层有3块小方块；中层比上层多3块，有3+3=6（块）；下层比中层多3块，有3+6=9（块）。