当前位置：文档之家 › 高考数学专题立体几何中的二面角的求法 优质课件ppt

高考数学专题立体几何中的二面角的求法 优质课件ppt

  • 格式：ppt
  • 大小：430.00 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

高一数学二面角的求法课件

高一数学二面角的求法课件


A

A O
l
O
10
B
B
二面角的平面角的作法：——
1、定义法
D1

A
C1
B1
O
A1 D A

B
C O B
例1.在正方体ABCD A1B1C1D1中, 试找出D1 AC D的平面角 , 求它的正切
二面角的计算步骤：
1、作出二面角的平面角
2、证明 1中的角就是所求的角 3、计算出此角的大小
O
B’
A
2.垂线法构造了对应的直 角三角形
作下面二面角的平面角
A D’ A’ B’ O C’
B
E
O
D C
D
C
二面角A--BC--D
A B 二面角B--B’C--A
例4.在正三棱柱 ABC A1B1C1中AC 1, AA A A1B C的正切 1 2, 连接A 1 B, A 1C , 求二面角
一“作”二“证”三“算”
例2.已知ABCD是边长为 2的正方形, PA 面AC且AP 1, 求二面角B C称性
A E D
B
C
二面角的平面角的作法：—— D1 A1 D A O B B1 C
1、定义法
C1
例1.在正方体ABCD A1B1C1D1中, 试找出D1 AC D的平面角 , 求它的正切
二面角的平面角的作法：——2、垂面法
P F P



l
F

l
O
E
O
E
例3.已知二面角 l , P为此二面角内一点 , 若PE垂直于E , PF垂直于F , 且PE 3, PF 4, EF 13, 求此二面角的大小

高考数学一轮复习课件——二面角PPT优秀课件

高考数学一轮复习课件——二面角PPT优秀课件


A A1 o o1
l
B1
B
22.05.2019
江西省赣州一中刘利剑 整理 heishu800101@
二面角的平面角
6、以二面角的棱上任意一点为端点，在两 个面内分别作垂直于棱的两条射线，这两条 射线所成的角叫做二面角的平面角。
二面角的大小用它的平面角来度量
？ ∠A O B
∠A1O1B1
――[阿萨·赫尔帕斯爵士] 115.旅行的精神在于其自由，完全能够随心所欲地去思考.去感觉.去行动的自由。――[威廉·海兹利特]
116.昨天是张退票的支票，明天是张信用卡，只有今天才是现金；要善加利用。――[凯·里昂] 117.所有的财富都是建立在健康之上。浪费金钱是愚蠢的事，浪费健康则是二级的谋杀罪。――[B·C·福比斯] 118.明知不可而为之的干劲可能会加速走向油尽灯枯的境地，努力挑战自己的极限固然是令人激奋的经验，但适度的休息绝不可少，否则迟早会崩溃。――[迈可·汉默] 119.进步不是一条笔直的过程，而是螺旋形的路径，时而前进，时而折回，停滞后又前进，有失有得，有付出也有收获。――[奥古斯汀] 120.无论那个时代，能量之所以能够带来奇迹，主要源于一股活力，而活力的核心元素乃是意志。无论何处，活力皆是所谓“人格力量”的原动力，也是让一切伟大行动得以持续的力量。――[史迈尔斯] 121.有两种人是没有什么价值可言的：一种人无法做被吩咐去做的事，另一种人只能做被吩咐去做的事。――[C·H·K·寇蒂斯] 122.对于不会利用机会的人而言，机会就像波浪般奔向茫茫的大海，或是成为不会孵化的蛋。――[乔治桑] 123.未来不是固定在那里等你趋近的，而是要靠你创造。未来的路不会静待被发现，而是需要开拓，开路的过程，便同时改变了你和未来。――[约翰·夏尔] 124.一个人的年纪就像他的鞋子的大小那样不重要。如果他对生活的兴趣不受到伤害，如果他很慈悲，如果时间使他成熟而没有了偏见。――[道格拉斯·米尔多] 125.大凡宇宙万物，都存在着正、反两面，所以要养成由后面.里面，甚至是由相反的一面，来观看事物的态度――。[老子]

高中数学空间向量与立体几何1.2.4二面角课件

高中数学空间向量与立体几何1.2.4二面角课件

则 sin θ＝
1－cos2θ
＝
55 10
.
即二面角 A-C1M-B1 的正弦值为
55 10
.
利用向量法求二面角的两种方法 方法一：分别在二面角 α­l­β 的面 α，β 内，沿 α，β 延伸的方向作向量 n1⊥l，n2⊥l， 则可用〈n1，n2〉度量这个二面角的大小． 方法二：通过法向量求解 设 m1⊥α，m2⊥β， 则〈m1，m2〉与该二面角相等或互补．
2．对射影面积公式的理解： (1)来源：三垂线定理． (2)适用范围：当二面角的一个半平面上的封闭图形的面积及它在另一个半平面上 的射影的面积已知或者已求出． (3)优势：不需要作出二面角的平面角．
如图，在直三棱柱 ABC-A1B1C1 中，AB＝1，AC＝AA1＝ 3 ，∠ABC＝60°.
(1)证明：AB⊥A1C； (2)求二面角 A-A1C-B 的正切值．
面角 A­ A1C­ B 的平面角．在 Rt△AA1C 中，AD＝AAA1·1CAC ＝
3× 6
36 ＝2 .
在 Rt△BAD 中，tan
∠ADB＝AABD
＝
6 3
，
6 所以二面角 A­ A1C­ B 的正切值为 3 .
类型三 利用向量法求二面角(逻辑推理、数学运算)
角度1
利用棱的垂线的方向向量求二面角
【思考】 二面角的大小、二面角的平面角的大小、两个相交平面所成角的大小的范围是相 同的吗？
提示：不相同．二面角的大小和二面角的平面角的大小的范围是[0°，180°] ，两 个相交平面所成角的大小的范围是[0°，90°] .
2．射影面积公式 已知平面 β 内一个多边形的面积为 S，它在平面 α 内的射影图形的面积为 S′，平 面 α 和平面 β 所成的二面角的大小为 θ，则 cos θ＝SS′ .

二面角的求法 PPT课件 人教课标版

二面角的求法 PPT课件 人教课标版
高中数学课件
二面角的求法
α
ι
β
一、二面角的定义
从一条直线出发的两个半平
面所组成的图形叫做二面角。
二、二面角的平面角
从棱上一点P分别在两 个半平面内作与棱垂直的 射线PA、PB则∠APB叫做二 面角 α-l-β的平面角。
ι
γ
P A
β
B
α
例1、已知正三 棱锥V-ABC所有的棱 长均相等，求二面角 A-VC-B的大小。
1、再长的路一步一步得走也能走到终点，再近的距离不迈开第一步永远也不会到达。 2、从善如登，从恶如崩。 3、现在决定未来，知识改变命运。 4、当你能梦的时候就不要放弃梦。 5、龙吟八洲行壮志，凤舞九天挥鸿图。 6、天下大事，必作于细；天下难事，必作于易。 7、当你把高尔夫球打不进时，球洞只是陷阱；打进时，它就是成功。 8、真正的爱，应该超越生命的长度、心灵的宽度、灵魂的深度。 9、永远不要逃避问题，因为时间不会给弱者任何回报。 10、评价一个人对你的好坏，有钱的看他愿不愿对你花时间，没钱的愿不愿意为你花钱。 11、明天是世上增值最快的一块土地，因它充满了希望。 12、得意时应善待他人，因为你失意时会需要他们。 13、人生最大的错误是不断担心会犯错。 14、忍别人所不能忍的痛，吃别人所不能吃的苦，是为了收获别人得不到的收获。 15、不管怎样，仍要坚持，没有梦想，永远到不了远方。 16、心态决定命运，自信走向成功。 17、第一个青春是上帝给的；第二个的青春是靠自己努力的。 18、励志照亮人生，创业改变命运。 19、就算生活让你再蛋疼，也要笑着学会忍。 20、当你能飞的时候就不要放弃飞。 21、所有欺骗中，自欺是最为严重的。 22、糊涂一点就会快乐一点。有的人有的事，想得太多会疼，想不通会头疼，想通了会心痛。 23、天行健君子以自强不息；地势坤君子以厚德载物。 24、态度决定高度，思路决定出路，细节关乎命运。 25、世上最累人的事，莫过於虚伪的过日子。 26、事不三思终有悔，人能百忍自无忧。 27、智者，一切求自己；愚者，一切求他人。 28、有时候，生活不免走向低谷，才能迎接你的下一个高点。 29、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。 30、经验是由痛苦中粹取出来的。 31、绳锯木断，水滴石穿。 32、肯承认错误则错已改了一半。 33、快乐不是因为拥有的多而是计较的少。 34、好方法事半功倍，好习惯受益终身。 35、生命可以不轰轰烈烈，但应掷地有声。 36、每临大事，心必静心，静则神明，豁然冰释。 37、别人认识你是你的面容和躯体，人们定义你是你的头脑和心灵。 38、当一个人真正觉悟的一刻，他放弃追寻外在世界的财富，而开始追寻他内心世界的真正财富。 39、人的价值，在遭受诱惑的一瞬间被决定。 40、事虽微，不为不成；道虽迩，不行不至。 41、好好扮演自己的角色，做自己该做的事。 42、自信人生二百年，会当水击三千里。 43、要纠正别人之前，先反省自己有没有犯错。 44、仁慈是一种聋子能听到、哑巴能了解的语言。 45、不可能！只存在于蠢人的字典里。 46、在浩瀚的宇宙里，每天都只是一瞬，活在今天，忘掉昨天。 47、小事成就大事，细节成就完美。 48、凡真心尝试助人者，没有不帮到自己的。 49、人往往会这样，顺风顺水，人的智力就会下降一些；如果突遇挫折，智力就会应激增长。 50、想像力比知识更重要。不是无知，而是对无知的无知，才是知的死亡。 51、对于最有能力的领航人风浪总是格外的汹涌。 52、思想如钻子，必须集中在一点钻下去才有力量。 53、年少时，梦想在心中激扬迸进，势不可挡，只是我们还没学会去战斗。经过一番努力，我们终于学会了战斗，却已没有了拼搏的勇气。因此，我们转向自身，攻击自己，成为自己最大的敌人。 54、最伟大的思想和行动往往需要最微不足道的开始。 55、不积小流无以成江海，不积跬步无以至千里。 56、远大抱负始于高中，辉煌人生起于今日。 57、理想的路总是为有信心的人预备着。 58、抱最大的希望，为最大的努力，做最坏的打算。 59、世上除了生死，都是小事。从今天开始，每天微笑吧。 60、一勤天下无难事，一懒天下皆难事。 61、在清醒中孤独，总好过于在喧嚣人群中寂寞。 62、心里的感觉总会是这样，你越期待的会越行越远，你越在乎的对你的伤害越大。 63、彩虹风雨后，成功细节中。 64、有些事你是绕不过去的，你现在逃避，你以后就会话十倍的精力去面对。 65、只要有信心，就能在信念中行走。 66、每天告诉自己一次，我真的很不错。 67、心中有理想 再累也快乐 68、发光并非太阳的专利，你也可以发光。 69、任何山都可以移动，只要把沙土一卡车一卡车运走即可。 70、当你的希望一个个落空，你也要坚定，要沉着！ 71、生命太过短暂，今天放弃了明天不一定能得到。 72、只要路是对的，就不怕路远。 73、如果一个人爱你、特别在乎你，有一个表现是他还是有点怕你。 74、先知三日，富贵十年。付诸行动，你就会得到力量。 75、爱的力量大到可以使人忘记一切，却又小到连一粒嫉妒的沙石也不能容纳。 76、好习惯成就一生，坏习惯毁人前程。 77、年轻就是这样，有错过有遗憾，最后才会学着珍惜。 78、时间不会停下来等你，我们现在过的每一天，都是余生中最年轻的一天。 79、在极度失望时，上天总会给你一点希望；在你感到痛苦时，又会让你偶遇一些温暖。在这忽冷忽热中，我们学会了看护自己，学会了坚强。 80、乐观者在灾祸中看到机会；悲观者在机会中看到灾祸。

二面角的求法(精华版)PPT课件

二面角的求法(精华版)PPT课件

二面角－AB－
A
C
B
二面角－ l－
D
l
B
A
二面角C－AB－ D .
F
E
A
Bபைடு நூலகம்
D
C
二面角C－AB－2E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
l
P
B
A
P1
B1
A1
二面角的大小用它的平面角的大小来度量 ∠APB= ∠A1P1B1
D1 E
C1
A1
B1
A FEB
G
A1
C
D
A
F
C
B
cos SAFCG
S A1FCE
F
练习3：三棱锥P-ABC中，PA ⊥平面 ABC，PA=3，AC=4，PB=PC=BC （1）求二面角P-BC-A的大小； （2）求二面角A-PC-B的大小。
P D
cos SABC
SPBC
AE
C
B
二、向量法：
1、方向向量法:
注意: 二面角的平面角必须满足：
1）角的顶点在棱上 (与顶点位置无关) 2）角的两边分别在两个面内 3）角的两边都要垂直于二面角的棱
二面角的平面角的范围: 0180
.
3
一、几何法：
1、定义法: 以二面角的棱a上任意一点O为端点，在两个面内
分别作垂直于a 的两条射线OA,OB，则∠AOB就 是此二面角的平面角。
将二面角转化为二面角的两个面 的方向向量（在二面角的面内垂 直于二面角的棱且指向该面方向 的向量）所成的角。
D

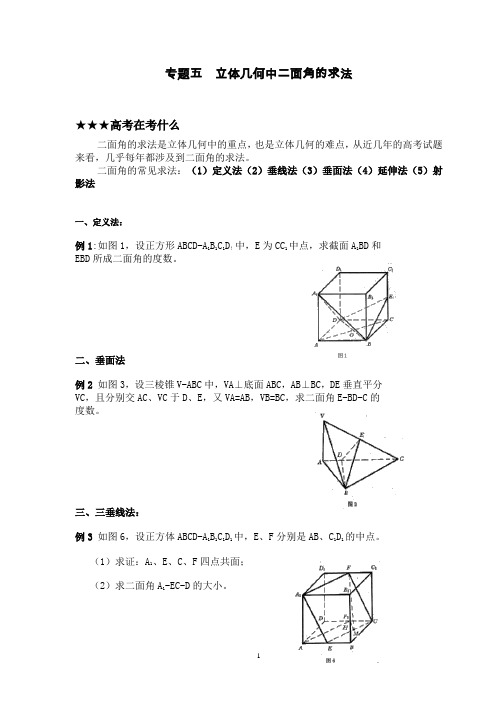
专题：立体几何中二面角的求法

专题：立体几何中二面角的求法

专题五立体几何中二面角的求法
★★★高考在考什么
二面角的求法是立体几何中的重点，也是立体几何的难点，从近几年的高考试题来看，几乎每年都涉及到二面角的求法。

二面角的常见求法：（1）定义法（2）垂线法（3）垂面法（4）延伸法（5）射影法
一、定义法：
例1:如图1，设正方形ABCD-A
1B
1
C
1
D
！
中，E为CC
1
中点，求截面A
1
BD和
EBD所成二面角的度数。

二、垂面法
例2如图3，设三棱锥V-ABC中，VA⊥底面ABC，AB⊥BC，DE垂直平分VC，且分别交AC、VC于D、E，又VA=AB，VB=BC，求二面角E-BD-C的度数。

三、三垂线法：
例3如图6，设正方体ABCD-A
1B
1
C
1
D
1
中，E、F分别是AB、C
1
D
1
的中点。

（1）求证：A
1
、E、C、F四点共面；
（2）求二面角A
1
-EC-D的大小。

四、延伸法
中点，
例4. 如图10，设正三棱柱ABC-A'B'C'各棱长均为α，D为CC
1
求平面A'BD与平面ABC所成二面角的度数。

五、射影法
例5如图12，设正方体ABCD-A1B1C1D1中，M为AA1上点，A1M:MA=3:1,求截面B1D1M与底面ABCD所成二面角。

高二数学 二面角(二) ppt(通用)


CD, ∵AE//CD,且AE=1 2
P CD
∴AE//FG,AE=FG,
从而四边形AEGF是平行四边形,
∴AF//EG, EG 平面PEC,
∴AF//平面PEC
A
.
E
B
B
C
.F
.
G
D
C
能力·思维·方法
8.在直角梯形P1DCB中，P1D∥CB，CD⊥P1D，P1D=
6，BC=3，DC=3，A是P1D的中点. 沿AB把平面P1AB
第九章 直线、平面、简单几何体
第7课时 二面角(二)
要点·疑点·考点
1.熟练掌握求二面角大小的基本方法：
(1)先作平面角，再求其大小；
(2)直接用公式
cos
S射 S原
2.掌握下列两类题型的解法：
(1)折叠问题——将平面图形翻折成空间图形.
(2)“无棱”二面角——在已知图形中未给出二面角 的棱.
基础题例题
面B1D1E和平面ABCD所成的二面角的正弦值.
解法二:取BC的中点F, 连接BD、EF, ∵E为BC的中点, ∴EF//BD,
D1
∵BD//B1D1, ∴EF//B1D1,
. C1
M
∴∴平E面FA、BBC1DD1∩共平面面，EB1D1F=EF，A1
B1
作BG⊥EF交FE的延长线于G,
连接B1G, 则∠B1GB是平面B1D1E
折起到平面PAB的位置，使二面角P-CD-B成45°，设
E、F分别为AB、PD的中点. P1
A
D
(1)求证：AF∥平面PEC；
(2)求二面角P-BC-A的大小；
证明:（2）∵CD⊥平面PAD, ∴平面PAD⊥平面ABCD

2.3.2二面角 数学 优秀课件

二面角的平面角必须满足： 1）角的顶点在棱上 2）角的两边分别在两个面内 3）角的两边都要垂直于二面角的棱
P A B
13
金太阳教育网

为什么要这样定义平面角？
品质来自专业 信赖源于诚信
1.唯一性
2.最大最小性


14
思考 ∠APB与∠A1P1B1是否相等?你能得出一个什
五，二面角的计算：
谢谢观赏
二面角
数学与统计学院 赖巧芳
复习引入
问题1：平面几何中“角”是怎样定义的？ 问题2：在立体几何中，“异面直线所成角”、
“直线和平面所成的角”又是怎样定义的？它
们有什么共同的特征？
角
图 形
平面角
异面直线所 成角
直线与平面所成角
B
b o a a
过O分别引直 a∥a,b∥b, 直线a和b所 成的锐角(或 直角)
归纳猜想：
Ａ
动态的二面角
Ｂ
Ｄ
Ｃ
问题情境2
打开笔记本电脑或课本时,两个面所成的二面 角给我们怎样的感觉?(变大?变小?） 如何刻画二成角呢？ 二面角可用平面角来度量。
归纳猜想：
金ห้องสมุดไป่ตู้阳教育网

4、平面角定义
品质来自专业 信赖源于诚信
以二面角的棱上任意一点为端点,在两个面 内分别作垂直于棱的两条射线,这两条射线所成 的角叫做二面角的平面角
么结论？ 二面角的大小可用其平面 角来度量，与点P的位置无 关。
P A B
P1
B1
A1 A 1
二面角范围 00≤α≤1800 直二面角：平面角是直角的二面角
例题精选
例1 在正方体ABCD－A1B1C1D1中

2025届高中数学一轮复习课件《二面角》ppt


∵PA＝AB＝2，∴AC＝BC＝ 2，PO＝ 3，∴OD＝ 2 2， ∴二面角 P-AC-B 的正切值是OPOD＝ 6.
高考一轮总复习•数学
(2)如图，在正三棱柱 ABC-A1B1C1 中，点 D 为 AC 的中点．
第16页
①证明：平面 AA1C1C⊥平面 DBC1； ②若 AB＝2，且二面角 D-BC1-C 的正切值为 615，求三棱柱 ABC-A1B1C1 的体积．
－ 即 －
2x1＋ 2y1＋
2z1＝0， 2z1＝0，
设平面 ABF 的法向量为 n＝(x2，y2，z2)，
取 x1＝1，则 y1＝z1＝AA··nn＝＝00，，
即
2x2＝0，
－ 2y2＋
2z2＝0，
得 x2＝0，取 y2＝1，则 z2＝1，n＝(0,1,1)．
高考一轮总复习•数学
第14页
对点练 1 (1)如图， 设 AB 为圆锥 PO 的底面直径，PA 为母线，点 C 在底面圆周上， 若 PA＝AB＝2，AC＝BC，则二面角 P-AC-B 的正切值是____6____．
高考一轮总复习•数学
第15页
(1)解析： 如图，取 AC 的中点 D，连接 OD，PD，易知 OD⊥AC，PD⊥AC，∴∠PDO 是二面角 P-AC-B 的平面角．
在 Rt△AB1C 中，S△AB1C＝12AB1·AC＝12B1C·AE，所以 AE＝ABB11·CAC＝2×2
2＝2
2 .
23
3
高考一轮总复习•数学
在 Rt△ADE 中，sin∠AED＝AADE＝ 2 ＝ 2 3. 22 3
所以∠AED＝60°，所以二面角 A-B1C-B 的大小为 60°.
第11页
高考一轮总复习•数学

高考数学复习第8章立体几何第9课时二面角理市赛课公开课一等奖省名师优质课获奖PPT课件

37/56
∵0<a<2，∴a＝1.∵h>0，∴h＝1，∴P(0，1，1)． ∴A→P＝(0，1，1)，A→C＝(1，1，0)，P→C＝(1，0，－1)，D→C＝ (1 ，－ 1， 0) ，设 平面 APC 的 法 向量 为 n＝(x， y， z) ， 由 n·A→P＝y＋z＝0， n·A→C＝x＋y＝0， 得平面 APC 的一个法向量为 n＝(1，－1，1)，
24/56
【解析】 设 α，β所成锐二面角为 θ， 则|cosθ|＝23，∴|n|n11|··n|n22||＝23. ∴|3－·22k0－＋1k02|＝23，∴k＝－12. 【答案】 －12
25/56
(2)(2018·辽宁丹东模拟)如图，正方形 A1BCD 折成直二面角 A－BD－C，则二面角 A－CD－B 的余弦值是( )
【答案】 6
17/56
题型二 向量法求二面角 (1)已知点 E，F 分别在正方体 ABCD－A1B1C1D1 的棱 BB1，CC1 上，且 B1E＝2EB，CF＝2FC1，则面 AEF 与面 ABC 所 成的锐二面角的正切值为________．
18/56
【解析】 如图，建立空间直角坐标系 D－xyz，
7 A. 21
3 C. 2
7 B. 4
3 D. 4
14/56
【解析】 如图所示，取 BC 的中点 P，
连接 EP，FP，由题意得 BF＝CF＝2，∴PF
⊥BC，又 EB＝EC，∴EP⊥BC，∴∠EPF 为
二面角 E－BC－F 的平面角，而 FP＝ FB2－（12BC）2＝ 27，
在△EPF
中，cos∠EPF＝EP22＋EPF·P2－FPEF2＝24×＋274×－9427＝
∵PH⊥平面 ABCD，∴z 轴∥PH. 则 A(0，0，0)，C(1，1，0)，D(0，2，0)，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

S
D(0，1 ，0)，S(0，0，1)，
B
C
2
易知平面SAB的法向量为 m =(0，1 ，0)；
2
设平面SDC的法向量为 n =(x，y，z)，
A
x
D
y
评或nn •• 其D注D CS补： 0角0 通）得过的此常例x规12 可y 方12 以yz法看是00 出构：造令求三n 二角x面=形(角1求，1大解2得小，，（1其y) 空关间键2面,又面是z角作等出于1二二面即面角角的
二面角的平面角的范围: 0180
一、几何法：
1、定义法:
以二面角的棱a上任意一点O为端点，在两个面内 分别作垂直于a 的两条射线OA,OB，则∠AOB就
是此二面角的平面角。
2、三垂线法:在一个平面内选一点A向另一平面 作垂线AB，
垂足为B，再过点B向棱a作垂线BO，垂足为O， 连结AO，则∠AOB就是二面角的平面角。
复 习: 二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角－AB－
A
C
B
二面角－ l－
D
l
B
A
二面角C－AB－ D
F
E
A
B
D
பைடு நூலகம்
C
二面角C－AB－ E
二面角的平面角:
以二面角的棱上任意一点为端
高考数学专题立体几何中的二面角的 求法 优质课件ppt
高考数学专题立体几何中的二面角的 求法 优质课件ppt
例：如图,在底面是一直角梯形的四棱锥S-ABCD中， AD∥BC,
∠ABC=90°，SA⊥平面AC，SA=AB=BC=1，AD= 1 .
求面SCD与面SAB所成的角的大小。
2
解法1：可用射影面积法来求，这里只要求
出S△SCD与S△SAB即可，
故所求的二面角θ应满足
cos S SAB
S S CD
1 11
=2
1 3 2
2
2
6
=
3
S
B
C
A
D
高考数学专题立体几何中的二面角的 求法 优质课件ppt
高考数学专题立体几何中的二面角的 求法 优质课件ppt
例：如图,在底面是一直角梯形的四棱锥S-ABCD中， AD∥BC, ∠ABC=90°，SA⊥平面AC，SA=AB=BC=1，AD= 1 .
高考数学专题立体几何中的二面角的 求法 优质课件ppt
高考数学专题立体几何中的二面角的 求法 优质课件ppt
（4）射影法是在不易作出平面角时用。在解答题中要先证 明射影面积公式，然后指出平面的垂线，射影关系，再用公 式,这种方法避免了找平面角，如果面积计算较简单，可用 此方法。 （5）当空间直角坐标系容易建立时，用向量法较为简洁明 快．用法向量求二面角的大小时，有时不易判断两法向量的 夹角大小就是二面角的大小(相等或互补)，但我们完全可以 根据图形得出结论，这是因为二面角是钝二面角还是锐二面 角一般是比较明显的．
高中数学核心素养——直观想象
高考立体几何中二面角的求法
考点分析：
立体几何是历年高考必考的热点，试 题难度中等，命题的热点主要有空间线 面位置关系的证明和空间角的求解；试 题背景有折叠问题，探索性问题等，考 查同学们的空间想象能力、逻辑思维能 力以及转化与化归思想的应用能力，解 决此类问题一般有常规方法和向量方法 ，用向量法解决此类问题可以化繁为简 ，降低题目的难度．
E
AF1SE 2SA 2
22
2
又∵DA⊥平面SAE，AF⊥SE
评∴注由三：垂常线规定理法得求D解F⊥步SE骤：一作：作出或找出相应空间角；
∴二∠D证FA：为通二面过角简的单平面的角判, 断或推理得到相应角；三求：通过计 ∴ta算nD求FA出＝相DFA应A 的22角。即所求二面角的正切值.
高考数学专题立体几何中的二面角的 求法 优质课件ppt
高考数学专题立体几何中的二面角的 求法 优质课件ppt
例∠A：B如C=图9,0在°底，面SA是⊥一平直面角A梯C，形S的A=四A棱B=锥BSC-=A1B，CDA中D=，1
AD∥BC, .
求面SCD与面SAB所成的角的大小。
解法3：（向量法） 如图，建立空间直角坐标系，
2
z
则A(0，0，0)，B(0，-1，0)，C(-1，1，0)，
αm
n
β
如图：二面角的大小等于<m ,n>
二、平面法向量法:
求二面角的大小，先求出两个半平面的法向 量的夹角，然后根据二面角与其大小相等或 互补求出二面角的大小。
m n
如图：二面角的大小等于-<m ,n>
高考数学专题立体几何中的二面角的 求法 优质课件ppt
几点说明：
（1）定义法是选择一个平面内的一点（一般为这个面的 一个顶点）向棱作垂线，再由垂足在另一个面内作棱的垂 线。此法得出的平面角在任意三角形中，所以不好计算， 不是我们首选的方法。
（2）三垂线法是从一个平面内选一点（一般为这个面的一 个顶点）向另一个面作垂线，再由垂足向棱作垂线，连结 这个点和棱上的垂足。此法得出的平面角在直角三角形中， 计算简便，所以我们常用此法。
（3）垂面法需在二面角之间找一点向两面作垂线，因为 这一点不好选择，所以此法一般不用。
以上三种方法作平面角都需写出作法、证明、指出平面角。
3、垂面法: 过二面角内一点A作AB⊥于B，作AC⊥ 于C，面 ABC交棱a于点O，则∠BOC就是二面角的平面角。
a
A
A
O B
A
B
a O
C
O a
B
4.射影面积法
A B
C
A1
B1
C1
cos S射影多边形
S多边形
二、平面法向量法:
求二面角的大小，先求出两个半平面的法向 量的夹角，然后根据二面角与其大小相等或 互补求出二面角的大小。
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
l
P
B
A
P1
B1
A1
二面角的大小用它的平面角的大小来度量 ∠APB= ∠A1P1B1
注意: 二面角的平面角必须满足：
1）角的顶点在棱上 (与顶点位置无关) 2）角的两边分别在两个面内 3）角的两边都要垂直于二面角的棱
2
求面SCD与面SAB所成的角的大小。
解法2：（三垂线定理法） 延长CD、BA交于点E，连结SE， S
SE即平面CSD与平面BSA的交线.又∵DA⊥平面SAB，∴过A
B
C
点作SE的垂线交于F.如图. ∵AD＝ 1 BC 且AD∥BC 2
F
A
D
∴△ADE∽△BCE ∴EA＝AB＝SA
又∵SA⊥AE ∴△SAE为等腰直角三角形，F为中点，