利用空间向量知识求空间中的二面角ppt课件

空间向量求二面角的方法方法一：先作出二面角的平面角，再利用向量的内积公式求解：设∠AOB 是二面角l αβ--的一个平面角,则向量OA 与OB 所成的角就是所求的二面角的大小．例1 正四面体ABCD 中，求相邻两个面所成的二面角．解析：如图1，取BC 边的中点Ｅ,连结AE 、DE ，则AE⊥BC，DE⊥BC，所以∠AED 就是正四面体的两个相邻面ABC 与DBC 所成二面角的平面角,且BC⊥平面ADE ，∴BC⊥AD，∴0EC DA =．设正四面体棱长为1．∵()()ED EA EC CD EC CD DA =+++ =222EC EC CD EC DA CD DA CD ++++ 11121cos120011cos1201424=+⨯⨯⨯++⨯⨯+=． 又在△ABC 与△BCD 中，可求得32ED EA ==, ∴cos ED EAED EA ED EA =，11433322==⨯． 故正四面体的两个相邻面所成的二面角大小为1arccos3．方法二:利用法向量求解:设1n 是平面α的法向量，2n 是平面β的法向量．①若两个平面的二面角如图2所示的示意图,则1n 与2n 之间的夹角θ就是欲求的二面角;②若两个平面的二面角如图3所示的示意图,设1n 与2n 之间的夹角为θ．则两个平面的二面角为πθ-． 例2 如图4，△ABC 是以∠B 为直角的直角三角形,SA⊥平面ABC ，SA=BC=2,AB=4，D 、N 分别是BC 、AB 的中点．求二面角S —ND-A 的余弦值．解析：平面ABC 的法向量是AS ,设平面SND 的法向量为BC AB AS λμ=++n ．∵SA⊥平面ABC ，∴SA⊥BC,SA⊥AB，∴0AS BD =,0AS BN =,0AS BC =，0AS AB = 又AB⊥BC,∴0BC BN =，0AB BD =,0BC NA =． 由()()ND BC AB AS BD BN λμ=++-n 280BC BD AB BN λμλμ=-=+=。

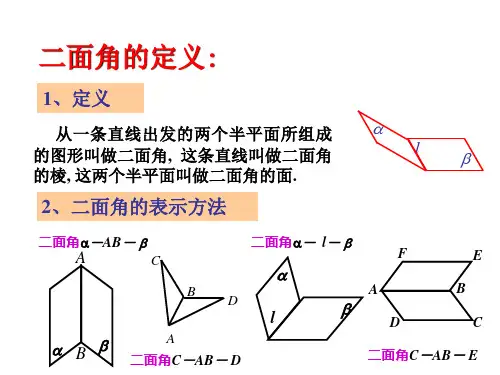
二面角二面角的求解方法（范围： ）一、定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；例、在四棱锥P -ABCD 中，ABCD 是正方形，PA⊥平面ABCD ，PA=AB=a ，求二面角B -PC -D 的大小。

变式：如图,已知二面角α-а-β等于120°,PA ⊥α,A ∈α,PB ⊥β,B ∈β. 求∠APB 的大小.二、三垂线定理法：已知二面角其中一个面内一点到一个面的垂线，用三垂线定理或逆定理作出二面角的平面角； 例、在四棱锥P -ABCD 中，ABCD 是平行四边形，PA⊥平面ABCD ，PA=AB=a ，⊥ABC=30°，求二面角P -BC -A 的大小。

p ABCDL HjA BC DPH ABCD A 1 B 1C 1D 1EOPOBA变式1、如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值.变式2、ΔABC 中，∠A=90°，AB=4，AC=3，平面ABC 外一点P 在平面ABC 内的射影是AB 中点M ，二面角P —AC —B 的大小为45°。

求（1）二面角P —BC —A 的大小；（2）二面角C —PB —A 的大小变式3、如图，平面α⊥平面β，α∩β=l ，A ∈α，B ∈β，点A 在直线l 上的射影为A 1，点B 在l 的射影为B 1，已知AB=2，AA 1=1，BB 1=2，求：二面角A 1－AB －B 1的大小.三、垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；例、空间的点P 到二面角βα--l 的面α、β及棱l 的距离分别为4、3、3392，求二面角βα--l 的大小.PlCBAB 1AA 1BLE FCDPMBA四、射影法（无棱二面角）利用面积射影公式S 射＝S 原cos θ,其中θ为平面角的大小，此方法不必在图形中画出平面角；例、在四棱锥P-ABCD 中，ABCD 为正方形，PA⊥平面ABCD ，PA ＝AB ＝a ，求平面PBA 与平面PDC 所成二面角的大小。

利用空间向量求二面角的平面角2 解：过D 作DF BC 于F ，过D 作DEFED 为二面角B AC D 的平面角， 又AB 平面BCD , AC 于E ，连结EF ，则AC 垂直于平面DEF ,• AB DF , AB CD , • DF 平面ABC ,• DF EF又••• AB CD , BD CD , • CD 平面 ABD , • CD AD ,设BD a ，贝U AB BC 2a , 在Rt BCD 中，S BCD 1-BC DF 21-BD CD , • DF 2.3 a1. 二面角的概念：二面角的定义•从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做 二面角的面.若棱为I ，两个面分别为 ，的二面角记为 丨2. 二面角的平面角：(1) 过二面角的棱上的一点 0分别在两个半平面内作棱的两条垂线 OA,OB ，则 AOB 叫做二面角 I 的平面角+(2)一个平面垂直于二面角 I 的棱I ,且与两半平面交线分别为 OA,OB, 0为垂足，则 AOB也是 I 的平面角+说明：(1) 二面角的平面角范围是 [0°,180°];(2) 二面角的平面角为直角时，则称为直二面角，组成直二面角的两个平面互相垂直 引导：请学生归纳已学过的求二面角的大小的方法，教师作必要的补充与引导•明确本节课的课题. 二. 求二面角的平面角：【回顾复习定义法求二面角的平面角】例 1：在棱长为1的正方体AC !中，求平面C^D 与底面ABCD 所成二面可以求得： sin COC 16，所以，平面GBD 与底面ABCD 所成3二面角C 1 BDC 的平面角的正弦值大小为63【回顾复习用三垂线法求二面角的平面角】例 2.如图，AB 平面BCD , BD CD ，若AB BC 2BD ，求.面角B AC D 的正弦值•分析：要求二面角的正弦值，首先要找到二面角的平面角角C 1 BD C 的平面角正弦值大小. 解：过C 1作C 1O BD 于点O ,•••正方体 AC 1 ,••• CC 1 平面 ABCD , 二 COC 1为平面GBD 与平面ABCD 所成二面角C 1G BD C 的平面角,C所以，二面角B AC D 的正弦值为一10 .5通过观察探究利用法向量解决： 例1 ：解：建立空间直角坐标系得：DC i (0,1,1)，DB (1,1,0)，DC (0,1,0)设平面 GBD 的法向量 n-i(x 1, y 1, Z |)，平面 CBD 的法向量 n 2 (x 2,y 2,z 2)，可得 n (1, 1,1)， n 2 (0,0,1)，口 (0,0,1) , n 2所以，二面角B AC D 的正弦值为一105三. 归纳小结：本节课回忆巩固了求解二面角的一些方法，并且通过类比用空间向量知识求解二面角，我们感受到空 间向量的巧妙之处，但要让同学们认识到法向量之间的夹角与二面角的平面角的异同之处。