X(六章3讲)变分法-氦原子

氦原子的线形变分波函数
氦原子（He）被认为是万物灵魂，它构成了星辰之间空间的大部分，也构成了
大气层和地壳的重要物质。

氦原子本质上是一个由两个电子组成的原子，它是目前已知最简单和最稳定的原子之一。

由于氦原子有非常简单的结构（只有两个电子），因此它的线形变分波函数非常容易计算。

线形变分波函数是描述原子的电子结构的重要理论工具。

它可以提供有关原子
的具体信息，比如工作函数、态密度和非核心相关能。

此外，它还可以用来描述原子内电子之间相互作用的态度和力学行为。

计算氦原子的线形变分波函数是一项艰难而又有趣的任务，它主要基于Hartree—Fock方程。

首先，需要使用Schrödinger方程来描述每个电子的电子态，然后使用Hartree-Fock方程来计算电子与空间相关态的势能，最后，通过在能级
和电荷上的变分求解Schrödinger方程来计算线形变分波函数。

经过上述复杂的数学处理，已经可以得到氦原子的线形变分波函数。

结果表明，氦原子的任何一级以上的电子态均可以用线形变分波函数来描述。

此外，我们也发现，氦原子在不同能级之间的能量差别主要来自相互作用，而不是原子核。

另外，计算结果还表明，氦原子中极小能级之间的跃迁主要受电子—电子作用的影响，而不是受原子核的影响。

由此可见，通过计算氦原子的线形变分波函数，我们可以获得有关氦原子的大
量信息，诸如氦原子内部的各种能级及电子态以及电子—电子作用。

通过对不同能级的分析，它们还可以让我们深入研究原子的电子态或电子结构的动力学行为。

氦原子和类氦离子基态能量的变分计算及相对论修正一、概述氦原子和类氦离子是一类重要的原子系统，它们的基态能量计算对于理解原子结构和相互作用具有重要意义。

在过去的研究中，许多学者针对氦原子和类氦离子的基态能量进行了理论和实验研究。

而其中变分计算和相对论修正是影响基态能量计算准确性的重要因素。

二、变分计算方法变分法是解决量子力学问题的一种重要方法，其基本思想是通过对波函数进行适当的变分，使得能量泛函达到最小值，从而得到系统的基态能量。

对于氦原子和类氦离子的基态能量计算，变分法被广泛应用。

1. 非相对论变分计算对于氦原子和类氦离子的非相对论变分计算，常采用数值方法求解Schrödinger方程，如Hartree-Fock方法、密度泛函理论等。

这些方法能够较好地描述非相对论情况下的基态能量，但不能考虑相对论效应对基态能量的修正。

2. 相对论变分计算相对论变分计算考虑了相对论效应对基态能量的修正，常见的方法包括Dirac方程、Breit方程等。

相对论修正可以提高对于高速运动的电子、以及高精度的原子性质和反应的描述能力。

相对论修正后的基态能量可以更好地符合实验结果。

三、相对论修正相对论修正是在非相对论基础上进行修正，包括狭义相对论和广义相对论两种情况。

对于氦原子和类氦离子，相对论修正主要包括以下几个方面：1. 狭义相对论修正狭义相对论修正主要考虑了电子的高速运动对基态能量的影响，可以通过Dirac方程和Klein-Gordon方程进行计算。

狭义相对论修正对于高速运动的电子体系基态能量的修正作用较为显著。

2. 广义相对论修正广义相对论修正考虑了引力场对基态能量的影响，常用的方法有考虑引力场的Dirac方程等。

在重力场较为强烈的情况下，广义相对论修正对基态能量的修正作用很大。

四、计算结果与讨论针对氦原子和类氦离子的基态能量，进行了变分计算和相对论修正。

通过数值计算得到了氦原子和类氦离子的基态能量，并与实验结果进行了比较。

氦原子s态的分波分析和强径——角关联区氦原子s态的分波分析和强径角关联区，是氦原子能量表面的一个有趣的特性。

它的存在可以帮助科学家和工程师更好地理解和推导复杂的化学反应，从而为更安全、有效和可靠的技术提供坚实的基础。

本文首先介绍氦原子s态分波分析，然后阐述强径角关联区，并讨论它在氦原子物理学和化学中的应用。

二、氦原子s态分波分析氦原子分子具有复杂的结构和能量表面。

氦原子s态分波分析（PAP）是一种用于研究复杂的氦原子结构和能量表面的数值方法。

分波分析可以更好地研究原子的能量状态，并可能提供关于聚合物的进一步信息。

由于PAP有助于研究原子的能量状态，这种方法也可以用来研究化学反应的特性和机理，从而更好地推导化学系统的运动学和动力学。

三、强径角关联区强径角关联区是由PAP得出的一种有趣而重要的特性。

角关联区是由氦原子在接近相连键方向的能量波函数构成的。

强径角关联区表明了在两个氦原子间存在强大的相互作用，表明两个氦原子之间存在着一种相对稳定的有机实体。

这种协同作用可能会在氦原子连接的分子中形成更加稳定的结构，从而影响其化学和物理性质。

四、氦原子物理学和化学的应用利用强径角关联区，科学家们可以更精确地预测和推断气体和液体中发生的化学反应。

它也可以用于研究氦原子化合物和有机分子的形成机理。

此外，强径角关联区在分子光谱研究中也发挥着重要作用。

例如，可以通过它来研究分子的光谱形态和精细结构，从而更好地预测分子的吸收和发射光谱特性，以及分子的化学反应。

五、结论氦原子s态的分波分析和强径角关联区是氦原子的一种重要特性。

它的存在可以帮助科学家和工程师更好地理解和推导复杂的化学反应，从而为技术开发提供可靠的基础。

氦原子s态分波分析和强径角关联区在氦原子物理学和化学中都发挥重要作用，可以用来研究和预测复杂的化学反应和物理学现象，进而为技术开发做出贡献。

氦原子基态能量实验及其运用变分法和微扰法两种方法比较【摘要】：对于由单电子粒子组成的两体问题，如氢原子或类氢离子，其基态能量本征值以及相应的波函数是可以通过薛定谔方程解析求解的，而且也很容易求解。

但对于多电子体系，即使是像氦原子和氢分子这样最简单的多电子体系，精确求解也是十分困难的。

因此，在量子力学中往往采用近似的方法来求解这类问题。

本文将以氦原子基态能量(实验测定值为-79eV)的求解为例，通过运用变分法和微扰法两种方法进行比较来解决多电子体系的基态能量求解问题。

【关键词】：氦原子 基态能量 变分法 微扰法 【引言】：在量子力学中，体系的能级和定态波函数可以通过求解定态薛定谔方程得到。

像一维无限深势阱、一维线性谐振子及氢原子等都能精确求解，但由于体系的哈密顿算符通常比较复杂，大多问题不能精确求解， 必须采用近似方法。

本文就氦原子基态能量分别用变分法和微扰法进行计算并加以比较。

【正文】：一、变分法的基本思想 设体系的定态薛定谔方程为ˆ,0,1,2n n nH E n ψψ==⋅⋅⋅ （1-1-1） 式中ˆH 的本征值012n E E E E <<⋅⋅⋅<<⋅⋅⋅，{}nψ是ˆH 的正交归一完备的本征函数系。

我们知道在任意态ψ中能量平均值0E E <，若随意选择一系列波函数计算E ,则最小的那个E 必最接近基态的能量0E ,而与之相应的那个波函数必最接近真正的基态波函数0ψ。

这就是变分法的基本思想。

由此得到求量子体系基态近似能量和近似波函数的方法。

二、利用变分法求氦原子基态的能级和波函数 1、氦原子的哈密顿算符氦原子由带电量为2e 的原子核和两个核外电子组成，由于核的质量比电子质量大得多，可以略去电子折合质量与电子质量的差异，氦原子的哈密顿算符为222222212121222ˆ22s s s e e e Hu r u r r =-∇--∇-+ （1-2-1） 式中u 为电子质量，1r 与2r 分别为两电子到核的距离，12r 是两电子间的距离。

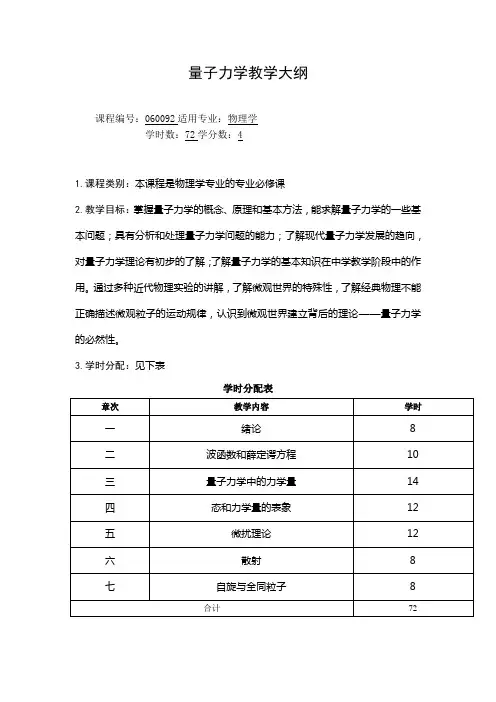
量子力学教学大纲课程编号：060092适用专业：物理学学时数：72学分数：41.课程类别：本课程是物理学专业的专业必修课2.教学目标：掌握量子力学的概念、原理和基本方法，能求解量子力学的一些基本问题；具有分析和处理量子力学问题的能力；了解现代量子力学发展的趋向，对量子力学理论有初步的了解；了解量子力学的基本知识在中学教学阶段中的作用。

通过多种近代物理实验的讲解，了解微观世界的特殊性，了解经典物理不能正确描述微观粒子的运动规律，认识到微观世界建立背后的理论——量子力学的必然性。

3.学时分配：见下表学时分配表第一章绪论教学时数：8学时重点难点：重点：了解经典物理遇到的困难，量子力学的建立过程。

微光粒子的波粒二象性。

难点：波粒二象性矛盾性的解释。

教学要求：了解：经典物理学的困难。

理解：波粒二象性矛盾性的辩证统一解释。

掌握：波粒二象性模型：λhP =的物理意义与它所包括的科学价值。

光的波粒二象性。

原子结构的波尔理论。

微光粒子的波粒二象性。

教学内容：（1）经典物理学的困难（2）光的波粒二象性（3）原子结构的波尔理论（4）微光粒子的波粒二象性第二章波函数和薛定谔方程教学时数：10学时重点难点：重点：波函数的统计解释，薛定谔方程的建立过程，用定态薛定谔方程处理势阱问题和线性谐振子问题。

难点：线性谐振子求解问题。

势垒贯穿。

教学要求：了解：量子力学理论的数学表示方式：薛定谔波动方程；波函数的统计解释。

理解：波粒二象性矛盾性的辩证统一解释——波函数的统计解释。

掌握：波函数的统计解释；定态薛定谔方程；一维无限深势阱的求解问题；定态薛定谔方程处理势阱问题和线性谐振子问题。

教学内容：（1）波函数的统计解释（2）态叠加原理（3）薛定谔方程（4）粒子流密度和粒子数守恒定律（5）定态薛定谔方程（6）一维无限深势阱（7）线性谐振子（8）*势垒贯穿第三章量子力学中的力学量教学时数：14学时重点难点：重点：表示力学量的算符；厄密算符本征函数的正交性；算符与力学量的关系。

原子物理与量子力学Atomic Physics and Quantum Mechanics哈尔滨理工大学应用科学学院应用物理系相关说明一、课程名称原子物理与量子力学二、计划学时108（每周3次6学时）三、课程性质技术基础课四、适用专业应用物理学、材料物理学、光信息科学与技术、电子科学与技术五、主要内容本课程内容主要可分为两大部分：1、原子物理学；2、量子力学。

原子物理学主要介绍原子物理学的发展。

从光谱学、X射线等方面的实验事实总结出能级规律，进一步分析原子结构的特点。

量子力学是二十世纪初建立起来的一门崭新的学科。

通过五个基本原理的引入，逐步构筑了量子力学的理论框架。

教学过程中，尽可能将两部分的相关内容结合讲授，利于学生理解和吸收。

原子物理学与量子力学是物理类学生的理论基础。

通过该课程的学习，学生应掌握有关原子等微观粒子的基本物理概念及反映其物理性质的基本规律，使学生了解和掌握现代一些重要的物理观念，并为应用技术准备理论基础。

六、教材与参考书《原子物理学》，褚圣麟，高教出版社《量子力学教程》，周世勋，高教出版社七、备注本课程采用多媒体教学，重点难点等采用特定的文字表现方式或动画声音等形式体现，可在“《原子物理与量子力学》课件”的相关章节观察效果。

目录绪论 (1)本章小结 (1)第一章原子的基本状况 (2)§1.1 原子的质量和大小 (2)§1.2 原子的核式结构 (2)本章小结 (3)第二章原子的能级和辐射 (4)§2.1 原子光谱的一般情况与氢原子光谱 (4)§2.2 经典理论的困难和光的波粒二象性 (4)§2.3 玻尔氢原子理论 (5)§2.4 类氢体系光谱 (5)§2.5 夫兰克-赫兹实验 (5)§2.6 量子化通则 (6)§2.7 电子的椭圆轨道 (6)§2.8 史特恩-盖拉赫实验与原子空间取向的量子化 (7)§2.9 量子理论与经典理论的对应关系对应原理 (7)本章小结 (7)第三章量子力学的运动方程—Schrödinger方程 (8)§3.1 物质的波粒二象性 (8)§3.2 波函数的统计解释 (8)§3.3 态叠加原理 (9)§3.4 薛定谔方程 (9)§3.5 几率守恒定律与定态薛定谔方程 (9)§3.6 一维无限深势阱 (10)§3.7 势垒贯穿 (10)§3.8 线性谐振子 (10)§3.9 电子在库仑场中的运动 (11)§3.10 氢原子 (11)本章小结 (12)第四章量子力学中的力学量 (13)§4.1 力学量算符 (13)§4.2 动量算符与角动量算符 (13)§4.3 厄密算符的本征函数 (14)§4.4 力学量的取值分布 (14)§4.5 算符的对易关系 (14)§4.6 测不准关系 (15)§4.7 守恒定律 (15)本章小结 (16)第五章碱金属原子的光谱和能级 (17)§5.1 碱金属原子的光谱和结构特点 (17)§5.2 碱金属原子光谱的精细结构 (17)§5.3 电子自旋与轨道运动的相互作用 (18)§5.4 单电子跃迁的选择定则 (18)*§5.5 氢原子光谱的精细结构与蓝姆移动 (18)本章小结 (19)第六章多电子原子 (20)§6.1 氦与第二族元素的光谱和能级 (20)§6.2 具有两个价电子的原子态 (20)§6.3 泡利原理与同科电子 (21)§6.4 复杂原子光谱的一般规律 (21)§6.5 辐射跃迁的普适选择定则 (21)§6.6 He-Ne激光器 (22)本章小结 (22)第七章磁场中的原子 (23)§7.1 原子的磁矩 (23)§7.2 外磁场对原子的作用 (23)§7.3 史特恩-盖拉赫实验的结果 (23)§7.4 顺磁共振 (24)*§7.5 物质的磁性 (24)§7.6 塞曼效应 (25)本章小结 (25)第八章原子的壳层结构 (26)§8.1 元素性质的周期性 (26)§8.2 原子的电子壳层结构 (26)§8.3 原子基态的电子组态 (26)本章小结 (27)第九章X射线 (28)§9.1 X射线的产生及测量 (28)§9.2 X射线的发射谱及相关能级 (28)*§9.3 X射线的吸收和散射 (28)*§9.4 X射线在晶体中的衍射 (29)本章小结 (29)第十章态和力学量的表象 (30)§10.1 态的表象 (30)§10.2 算符的矩阵表示 (30)§10.3 量子力学公式的矩阵表述 (31)§10.4 幺正变换 (31)§10.5 狄拉克符号 (31)§10.6 占有数表象 (32)本章小结 (32)第十一章微扰理论 (33)§11.1 非简并定态微扰理论及其应用 (33)§11.2 简并情况下的微扰理论及其应用 (33)§11.3 变分法与氦原子基态 (34)§11.4 与时间有关的微扰理论 (34)§11.5 跃迁几率 (34)§11.6 光的发射与吸收 (35)*§11.7 选择定则 (35)本章小结 (36)第十二章散射 (37)§12.1 碰撞过程与散射截面 (37)§12.2 中心力场中的弹性散射（分波法） (37)本章小结 (37)第十三章自旋与全同粒子 (39)§13.1 电子的自旋 (39)§13.2 电子自旋的描述 (39)§13.3 简单塞曼效应 (40)§13.4 角动量的耦合及应用 (40)§13.5 光谱的精细结构 (41)§13.6 全同粒子体系 (41)§13.7 全同粒子体系的波函数 (41)§13.8 两个电子的自旋函数 (42)本章小结 (42)绪论绪论本章主要介绍原子物理与量子力学的发展过程，并指出学习新理论应注意的问题。

高中化学人教版必修一第六章知识点总结本文档总结了高中化学人教版必修一第六章的重点内容。

第一节电子的发现与性质- 电子的发现：详细介绍了通过阴极射线实验证明了电子的存在以及电子的基本性质。

- 电子的性质：讲解了电子的质量、电荷、自旋等性质，并介绍了电子的波粒二象性。

第二节原子的发现与性质- 原子的发现历史：回顾了道尔顿提出的原子学说，以及后来通过实验证实了原子存在的事实。

- 原子的性质：介绍了原子的基本结构，包括原子核和电子云，并解释了电子云模型和量子力学模型。

第三节原子结构变化和元素周期表- 原子结构变化：说明了原子在化学反应中的结构变化，包括电离和激发。

- 元素周期表：介绍了元素周期表的基本结构，包括周期和族的概念，并解释了周期表中元素性质的规律性。

第四节原子质量与元素相对原子质量- 原子质量：介绍了原子质量的概念和测定方法。

- 元素相对原子质量：讲解了相对分子质量、相对原子质量和摩尔质量之间的关系，并介绍了计算相对原子质量的方法。

第五节化学式与物质的量计算- 化学式：介绍了化学式的概念，包括分子式、离子式和结构式，并解释了化学式的应用。

- 物质的量计算：讲解了物质的量的概念和计算方法，包括摩尔、物质的量分数和化学反应物质的计量关系。

第六节化学变化中的能量变化- 化学反应中的能量变化：说明了化学反应中可能发生的能量变化，包括放热反应和吸热反应。

- 化学反应的热力学方程式：介绍了计算放热反应和吸热反应的热力学方程式，并解释了热化学方程式的应用。

第七节完全反应与未完全反应- 完全反应和未完全反应：比较了完全反应和未完全反应的特点，并解释了未完全反应的原因。

- 反应的计算：讲解了通过化学方程式计算反应物质的方法，并介绍了反应的收率和原子经数的概念。

第八节氧化还原反应- 氧化还原反应：介绍了氧化还原反应的基本概念，包括氧化剂、还原剂和氧化数，并解释了氧化还原反应的电子转移过程。

第九节电解质溶液- 电解质溶液：讲解了电解质溶液中的离子行为，包括电离和导电性，并解释了电解质溶液的电解作用。

中学科普类文章——氦（He）氦——它，来自太阳，人类却在月亮上继续找它元素周期表一百余号元素，大家熟知排名第一的氢，往往忽略了排名第二的元素——氦（Helium），元素符号为He。

其实，氦（He）是一个名副其实的“宝藏男孩”，无论是“想带你去浪漫的土耳其”的热气球填充气体、还是沙巴芭堤雅潜水罐里的气体，都离不开氦气。

这些都和氦气本身的特性离不开。

今天，我们就来聊聊这个“宝藏男孩”——氦气来自太阳的神秘588谱线英文中男性第三人称“他”也是He，跟氦一样——这可不是巧合，因为两个He 都跟太阳有关。

男性自然是阳性，跟太阳有关；氦是从对太阳的研究中发现的。

1868年法国天文学家的杨森（Georges Rayet）利用分光镜观察太阳表面时，发现了新的黄色谱线。

这个发现被他的法国同行简森（Pierre Janssen）确证之后写了篇paper提交给法国科学院。

与此同时，专业研究太阳的英国科学家洛克耶爵士（Sir Joseph Norman Lockyer）在伦敦也观察到了这条波长为588纳米的谱线。

凭借敏锐的洞察力，他推断这是新元素，并以希腊语的Helios（太阳）对其命名为Helium。

顺便，这位洛克耶，是《Nature》的创办者和首任编辑。

看见了，摸不着？这可不行！发现He之后的二十多年里，不同国家的科学家都在想办法从地球上寻找这个元素。

1895年春天，苏格兰化学家拉姆西爵士（Sir William Ramsay）从钇铀矿石里首先得到了氦气。

当时拉姆西想弄点氩气，他用酸处理矿石后得到些气体，然后他把气体中的氮气和氧气除掉，用光谱法检测剩余的气体，竟然发现了588纳米的谱带。

他把这份气体样品交给近水楼台先得月的洛克耶爵士分析，洛克耶确认这就是他命名的He。

差不多相同时间，瑞典一对科研好基友也在研究钇铀矿，克莱夫（Per Teodor Cleve）和兰吉特（Abraham Langlet）一起独立分离了大量高纯度的氦气，并且精确测定了分子量。

氦原子基态能量实验及其运用变分法和微扰法两种方法比较【摘要】：对于由单电子粒子组成的两体问题，如氢原子或类氢离子，其基态能量本征值以及相应的波函数是可以通过薛定谔方程解析求解的，而且也很容易求解。

但对于多电子体系，即使是像氦原子和氢分子这样最简单的多电子体系，精确求解也是十分困难的。

因此，在量子力学中往往采用近似的方法来求解这类问题。

本文将以氦原子基态能量(实验测定值为-79eV)的求解为例，通过运用变分法和微扰法两种方法进行比较来解决多电子体系的基态能量求解问题。

【关键词】：氦原子 基态能量 变分法 微扰法 【引言】：在量子力学中，体系的能级和定态波函数可以通过求解定态薛定谔方程得到。

像一维无限深势阱、一维线性谐振子及氢原子等都能精确求解，但由于体系的哈密顿算符通常比较复杂，大多问题不能精确求解， 必须采用近似方法。

本文就氦原子基态能量分别用变分法和微扰法进行计算并加以比较。

【正文】：一、变分法的基本思想 设体系的定态薛定谔方程为ˆ,0,1,2n n nH E n ψψ==⋅⋅⋅ （1-1-1） 式中ˆH 的本征值012n E E E E <<⋅⋅⋅<<⋅⋅⋅，{}nψ是ˆH 的正交归一完备的本征函数系。

我们知道在任意态ψ中能量平均值0E E <，若随意选择一系列波函数计算E ,则最小的那个E 必最接近基态的能量0E ,而与之相应的那个波函数必最接近真正的基态波函数0ψ。

这就是变分法的基本思想。

由此得到求量子体系基态近似能量和近似波函数的方法。

二、利用变分法求氦原子基态的能级和波函数 1、氦原子的哈密顿算符氦原子由带电量为2e 的原子核和两个核外电子组成，由于核的质量比电子质量大得多，可以略去电子折合质量与电子质量的差异，氦原子的哈密顿算符为222222212121222ˆ22s s s e e e Hu r u r r =-∇--∇-+ （1-2-1） 式中u 为电子质量，1r 与2r 分别为两电子到核的距离，12r 是两电子间的距离。

第一章绪论1.1引言对氦原子基态能级的探讨一般选用微扰法及变分法，本文重点讨论变分法对氦原子基态能级的求解。

变分法是解决氦原子和类氦离子基态问题的强有力工具，到目前为止，国内外为追求高精度所选取的变分参数个数已由数百增至数千，在忽略核质量的情况下，它们的非相对论基态波函数和能量的不确定度分别达到109-～1010-和1019-，这对于计算高精度的相对论修正和辐射修正具有非常重要的意义。

在量子力学教科书中，一般介绍的近似求解法是微扰法和变分法，而变分法中选择的尝试波函数一般是一个参数型的，例如周世勋编《量子力学》、曾谨言著《量子力学教程》等介绍的便是用一个参数型的尝试波函数变分法求氦原子体系基态能级。

l.2选题的依据和意义1.2.1选题的依据在量子力学中，对于具体物理问题的薛定谔方程，可以精确求解的问题是很少的。

在经常遇见的许多问题中，由于体系的哈密顿算符比较复杂，往往不能求得精确的解，而只能求近似解。

微扰法和变分法都是用来求问题的近似解的方法。

用微扰法求氢原子和类氢离子是比较适合的，但是遇到比氢原子稍微复杂一点的氦原子时，微扰法就不及变分法容易和求解精确。

用一参变分法即选用含一个参数的尝试波函数，这种波函数形式简单，其物理意义清晰，物理模型简单，适用于教育教学，但精确度比较低。

选用含二参数的尝试波函数，这样的模型相对于更多参数的波函数要简单，又比一参变分法求解精确度高很多，这样既有利于理解怎样用变分法求基态能级，可适用于教学,又能求得比一参法更为精确的数值，因而具有重要的物理意义。

1.2.2选题的意义氦原子是比类氢离子这种单粒子体系复杂但是相对于其他粒子要简单的粒子，研究氦原子这种简单的多粒子体系，对于研究更复杂的多粒子体系具有重要的意义。

变分法是解决氦原子和类氦原子的强有力工具，只要选择合适的试探波函数，对于提高求解能级近似值有很大的帮助。

l.3本文的主要研究内容本文主要研究氦原子的基态能级，通过应用双参数变分法，选择适当的试探波函数，求出氦原子基态能级的能量，并将计算值与试验值进行比较，再与用微扰法求出的氦原子基态能量结果进行对比，通过对比体现出用变分法求氦原子基态能级的优越性。